海底地形對洋中脊熱液對流活動的影響研究
——基于海水壓力的空間變化

范慶凱，李江海*

( 1. 北京大學 地球與空間科學學院 造山帶與地殼演化教育部重點實驗室，北京 100871；2. 北京大學 石油與天然氣研究中心，北京 100871)

1 引言

洋中脊熱液對流循環是地殼熱量輸出的主要方式，通過這種方式輸出的總熱量大致可占全球地殼熱輸出的25%[1]，也是新生洋殼產生和地球化學循環的主要影響因素[2–3]。在洋中脊擴張中心，海水沿洋殼內的斷裂?裂隙系統向下滲透至巖漿侵入體附近，在巖漿熔體等熱源的加熱和驅動下與圍巖發生熱化學反應并逐漸匯集上涌，形成富集的熱液礦體。

前人研究結果表明，影響洋中脊熱液對流系統的因素包括洋殼滲透率結構、熱源位置與溫度，以及洋殼增生模式等[4–9]。洋殼內部熱液對流的形態直接取決于各方向的流體壓力梯度，熱液流體傾向于沿高流體壓力梯度向低壓區匯集、噴發。洋底地形起伏引發的下伏洋殼流體壓力梯度變化也導致了熱液噴發活動多發育于洋底高地形[10]。發育于快速和慢速擴張洋中脊的多個熱液區（如東太平洋海隆（EPR）9°17′N 熱液區和大西洋洋中脊Lucky Strike 熱液區）直接證明了海底地形對其下伏熱液對流系統的影響。相關的解析模型和數值模擬研究表明洋底高地形對熱液上涌和噴發的匯聚作用[11–13]。

然而，除了引起下伏洋殼內部流體壓力梯度的變化之外，洋底地形起伏相關的水深變化也直接導致了洋底上覆海水壓力的變化，即高地形上覆壓力較低，低地形則較高。這種海水壓力的空間變化是否會對洋殼內部熱液對流形態產生影響，從而導致其沿高地形匯聚、噴發仍不得而知。本文主要從這一方面入手，通過基于彈性孔隙模型的數值模擬，主要聚焦于洋底地形起伏引起的上覆壓力跨軸變化對下伏熱液對流系統的形態和熱液噴發位置的影響，即基于洋底上覆壓力的單因素研究。旨在探索一個可以定量描述海底高地形和熱液對流系統的橫向偏移程度之間關系的實驗模型，并結合實際觀測[14–18]，對比不同類型洋中脊的熱液活動。

2 研究方法與數據來源

本文應用基于彈性孔隙模型的有限體積模型，基于Matlab 計算平臺運行。該模型通過孔隙介質中達西流體的運動規律來模擬洋殼內部實際的熱液對流活動，具體的模擬方法與文獻[19]相似，但采用不同的初始、邊界條件，來探討海水壓力的空間變化這一單因素的影響。另外，我們選擇EPR 9°17′N 熱液區和Lucky Strike 熱液區作為對比實例，主要因為：（1）兩個研究區分別屬于快速擴張洋中脊和慢速擴張洋中脊，從而更具全面性；（2）二者皆發育有不同規模的高溫熱液活動（前者噴發溫度約388℃，后者約333℃，引自Interridge 數據庫[20]），且均噴發于洋底高地形；（3）在二者下伏洋殼內均發現了可維持熱液對流活動的地震波速異常[14,17]，從而可以直觀、合理地對比熱源的位置和規模。其中，EPR 9°17′N 熱液區和Lucky Strike 熱液區的跨軸地形數據均引自海洋地學數據庫系統（MGDS, http://www.marine-geo.org/portals/gmrt/[21]）。

3 熱力學數值模擬

3.1 控制方程

本文的數值模型通過應用基于布辛涅司克近似定義（Boussinesq Approximation）[19,22]的達西定律來解孔隙介質中的流體和熱量傳導方程，以獲得不同時間的流體速度和溫度。在這種基本框架內，模型中流體的質量守恒定律可以表述為

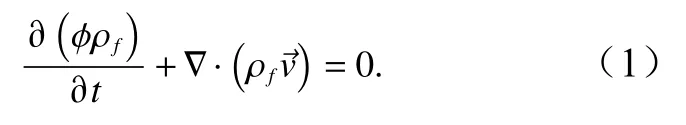
方程（1）對應基于單相流體充填、各向均一介質的對流模型。式中，ρf為流體密度；?為模型基質孔隙度；為達西流體速度，可通過達西定律直接獲得，即

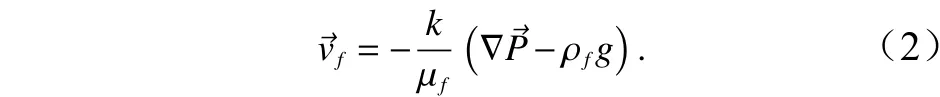
孔隙介質熱傳遞方程[23]可表述為

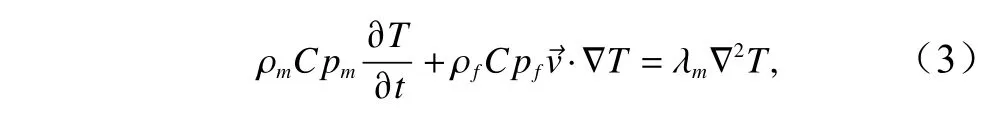
式中，T為溫度；t為時間；ρm和Cpm分別代表流體?圍巖混合體的密度和比熱容；Cpf為流體比熱容；λm為流體?圍巖混合體的熱傳導系數。上覆箭頭則代表矢量參數。

關于流體參數，本文應用溫度、壓力相關的非線性流體性質（密度、黏度、比熱容等[24–26]）。而基于簡化的線性流體方程，流體密度可視為溫度的線性函數，即

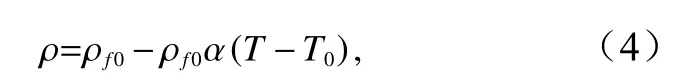
式中，ρf0和T0分別表示海水的密度和溫度；α為熱擴張系數；T為洋殼內部流體溫度。

在洋殼內部熱傳導的背景下，當熱液流體的達西速率遠大于熱傳導速度時，洋殼內部明顯的熱液對流循環得以發生，二者的比值即為瑞麗數（Ra），即

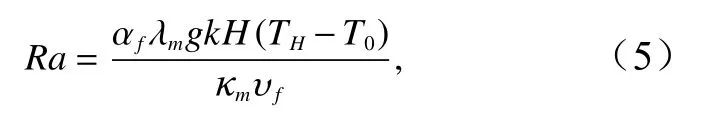
式中，αf為流體熱擴張系數；κm為流體?圍巖混合體熱擴散系數；υf為流體的運動學黏度；TH為熱源溫度；H為模型高度；λm為熱傳導系數。當瑞麗數大于特定的臨界值（Rac）時，熱液對流最終產生，該臨界值會隨著模型的形狀、參數等變化，具體數值可由實驗獲得。另外，瑞麗數的大小直接與熱液對流系統的強度呈正相關關系，瑞麗數越大，熱液對流越劇烈，反之則越微弱[9,27]。

熱傳導的輸出功率（QC）可由海底熱擴散溫度與下伏熱源溫度差、模型高度等參數獲得，即

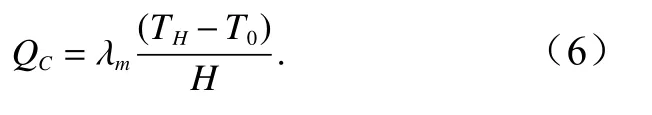
洋底的總熱量輸出（Q）通常表現為洋殼內部熱對流與熱傳導功率的總和，與熱傳導輸出量的比值稱為納賽爾數（Nu>1），即

Nu與熱液對流系統的Ra表現為線性相關（ζ～0.1）：

因此，可最終獲得洋中脊總熱量輸出功率為

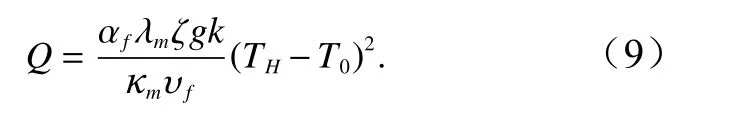
3.2 模型設置與邊界條件

本文應用的模型為長方形塊體，代表洋中脊軸向或離軸一定距離（l=20km）和深度（h=10km）的剖面（圖1）。模型主體為具有固定孔隙度（3%）的滲透層[22]，代表以噴發性玄武巖為主的洋殼。上界為海底面，設置為對流體開放的邊界，并賦予固定（20 MPa）或變化的上覆壓力和溫度（0℃），代表固定或變化的海水深度和海底地形起伏。模型的邊界和底界均被設置為絕熱、封閉的邊界。

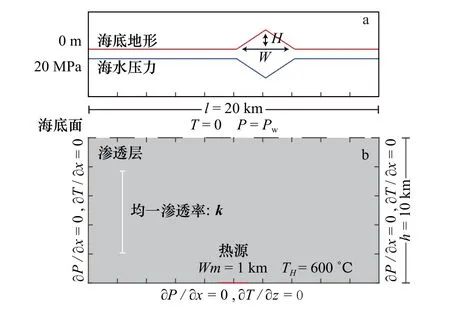
圖1 模型設置與邊界條件Fig. 1 Model setup and boundary conditionsa. 上覆壓力分布與其所代表的海底地形起伏示意圖;b. 模型尺寸與邊界條件a. Schematic sketch for the distribution of overlying pressure and bathymetric relief; b.model size and boundary conditions

為了研究洋殼上覆海水壓力的單因素影響，排除包括難以預測的洋殼滲透率結構[28–29]和洋殼增生方式對洋殼內部熱液對流形態的潛在影響，并鑒于模型運行的時間成本，本文賦予模型各向均一分布的滲透率 值（k=1×10?15m2）。依 據 前 人 研 究 結 果[30]，高 于600℃的洋殼層位可被視為非滲透層，且在發育有穩定巖漿透鏡體的快速?中速擴張洋中脊，其透鏡體的寬度均在1km 左右[31–32]。基于上述原因，我們將固定溫度（600℃）、固定寬度（1km）的高溫區域設置于模型底界的中心位置，代表驅動、維持上覆熱液對流循環的熱源。海底上覆壓力的變化及其代表的海底地形起伏作為數值模擬的唯一變量，主要通過設置一定高度（H）和寬度（W），且兩側固定的高地形（圖1a）來實現，高地形之外統一設置為平坦地形。與洋底地形相關的海水深度直接決定了海底上覆壓力的分布（圖1a）。其中，高地形高度值分布范圍為5～150m，寬度則分別為2000m、4000m、6000m 和8000m，且高地形左側起點與熱源中心位置保持在相同的水平位置（圖1b）。

為了研究穩態下熱液噴發位置和地形高點間的關系，我們將各模型分別運行至1～10 Ma 不等，以確保其全部達到穩態。

4 研究結果

4.1 數值模擬結果

經過模擬不同規模高地形引發的海底上覆海水壓力變化對其下伏熱液對流系統形態的影響，本文最終獲得約120 組穩態數值模擬結果（海底高地形起伏值5～150m，以5m 為間隔，高地形起伏寬度值分別為2000m、4000m、6000m 和8000m）。基于數值模擬結果，不同規模的地形起伏會使下伏熱液系統產生不同程度的橫向偏移，最終致使洋殼內部熱液羽向海水壓力低值點（地形高點）匯集。

綜合所有模擬結果，洋殼內部上升熱液羽表現為大致相同的寬度（約3km）和相似的熱液噴發溫度（約250℃）以及熱流輸出功率。當海水壓力低值為19.5 MPa（對應地形高度約50m），壓力低異常區寬度為約2km 時（圖2a），下伏高溫熱液羽表現為一定程度地向海底低壓區轉移的現象，具體表現為偏離原始熱源位置約800m（圖2b）。保持海底低壓區的規模不變，將其谷值減小至19 MPa（圖2c，對應100m 的地形高度），洋殼內部熱液羽則表現為明顯的偏移，完全匯聚并噴發于海水壓力低值點（地形高點，圖2d）。

將地形起伏區增加至4km 寬，最大高度保持為50m（圖2e），洋殼內部熱液羽表現為偏離熱源位置約1700m，并向海底壓力低值區（高地形點）轉移的特征（圖2f）。相似地，在地形起伏規模不變的基礎上，進一步減小地形高點的海底壓力極值（至約19 MPa，對應100m 高的地形高點，圖2g），洋殼內部熱液對流系統則表現為完全程度的偏離和匯聚效應，即海底熱液噴發位置完全與海底高地形點重合（圖2h）。

綜合上述現象，并結合所有的模擬輸出結果（圖3），海底地形起伏的橫向寬度和縱向高度均會對洋殼內部熱液對流系統的形態產生不同程度的偏移影響，具體表現為海底高地形規模和地形起伏程度的增加均會明顯提升其對洋殼內部熱液對流系統的偏移影響。在特定海底高地形寬度的情況下，洋殼內部上升熱液羽會在某一特定臨界高度值形成完全程度的偏移效果，即海底熱液噴發完全集中于地形高點的位置（圖3a），并且此臨界值表現為隨海底高地形寬度的增加而增加的趨勢。同理，洋殼內部熱液羽的橫向偏移角度可根據相應的偏移距離得出（圖3b），并表現出類似的規律。

4.2 解析模型

依據模擬得出的洋殼內部熱液羽偏移距離和偏移角度的統計結果（圖3），我們可以通過一定的統計學規律來獲得可以定量描述海底地形起伏（海底上覆壓力變化）與洋殼內部熱液羽偏移程度以及熱液噴發位置的解析模型，

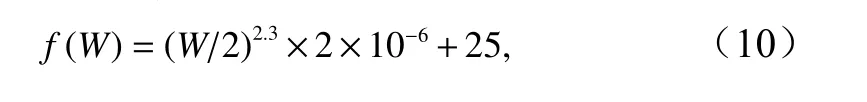
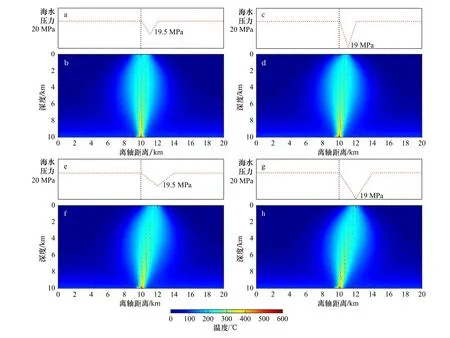
圖2 數值模擬結果Fig. 2 Simulation resultsa. 2000m×50m 高地形數值模擬結果; b. 2000m×100m 高地形數值模擬結果; c. 4000m×50m 高地形數值模擬結果; d. 4000m×100m高地形數值模擬結果a. Simulation with a bathymetric high of 2000m×50m; b. simulation with a bathymetric high of 2000m×100m; c. simulation with a bathymetric high of 4000m×50m; d. simulation with a bathymetric high of 4000m×100m

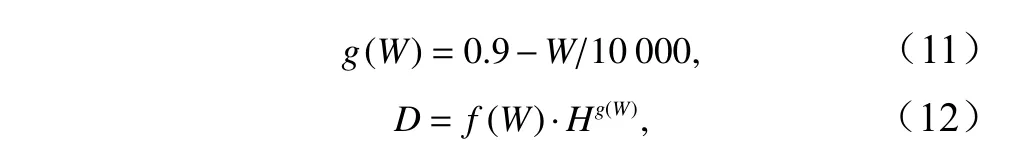
式中，W為海底高地形起伏的寬度；H為海底高地形起伏極值的高度；D表示洋殼內部熱液羽的偏移距離。

依據獲得的基于統計學的解析模型，洋殼內部熱液羽向高地形的偏移距離（圖4a）和偏移角度（圖4b）均由海底高地形的規模決定。基于該模型（圖4），洋殼內部熱液羽的偏移程度表現為最大偏移距離約5km 和最大偏移角度約26°，二者均表現為海底高地形起伏的寬度和高度的函數，且海底地形越高，規模越大，下伏熱液羽向高地形的偏移程度就越大，符合上述模擬結果（圖2）。

5 討論

上述數值模擬結果表明海底上覆海水壓力的不均一分布會最終導致洋殼內部熱液對流系統向海底高地形區域匯集并噴發，這也符合前人的研究結果[11–13]。本節主要聚焦于現今仍在活動的洋中脊熱液系統，應用熱液系統相關的實際海底地形剖面和已知的巖漿熱源尺寸與位置，來探究實際的海底地形對熱液對流系統的偏移影響。

5.1 EPR 9°17′N 熱液區熱液活動

東太平洋海隆是典型的快速擴張洋中脊（全擴張速率約110～150mm/a[33]，EPR 9°17′N 及其相鄰區域表現為相對平緩的跨軸地形變化和洋脊軸處相對較高的地形[18,34–35]（圖5a），并在下伏約1.5km 的深度發育連續的透鏡狀巖漿熔融體[3]，EPR 9°17′N 熱液區即為發育于該研究區軸部高地形[15]（圖5a）的高溫熱液活動區（約388℃, 引自Interridge 數據庫[20]）。依據研究區跨軸水深分布，我們計算出研究區跨軸海水壓力剖面（圖5b），并將其設置為模型上界的壓力邊界條件。

基于EPR 9°17′N 熱液活動區的實際情況（包括上覆海水壓力的跨軸變化和下伏巖漿熱源的規模、位置），我們將模型設置為10km×3km，代表10km 的跨軸距離和3km 的洋殼厚度，高溫（約600℃，寬度約為2km）熱源位于模型底界中央，代表EPR 9°17′N熱液活動區下伏的連續性巖漿透鏡體（圖5c），同時將模型滲透率設置為均一值（約11×10?15m2）。運行該模型至 100 ka，確保其到達穩定狀態。

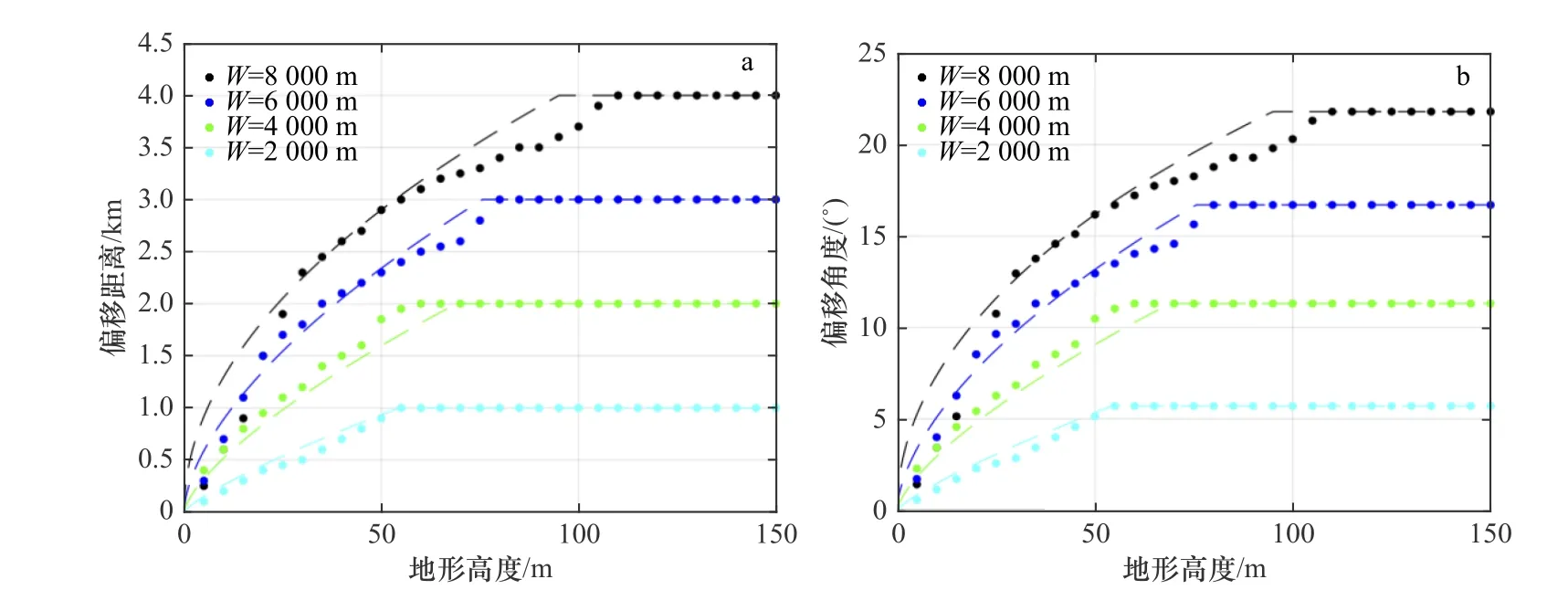
圖3 熱液羽偏移程度與地形高度的關系Fig. 3 Relationship between deviation of fluid plumes and height of bathymetric highsa. 熱液羽偏移距離與地形高度的關系; b. 熱液羽偏移角度與地形高度的關系a. Relationship between deviation distance of plumes and height of bathymetric highs; b. relationship between deviation degree of plumes and height of bathymetric highs

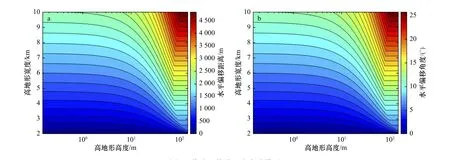
圖4 熱液羽偏移程度實驗模型Fig. 4 Experimentalmodel of the deviation of plumesa. 熱液羽偏移距離實驗模型; b. 熱液羽偏移角度實驗模型a. Model of the deviation distance of plumes; b.model of the deviation degree of plumes

依據穩態數值模擬結果（圖5c），EPR 9°17′N 下伏洋殼發育約1km 寬的高溫（約330℃）熱液羽，并離軸向洋脊軸高地形偏移約1km 的水平距離，最終的熱液噴發位置與實際的EPR 9°17′N 熱液區位置（圖5a）保持高度一致，表明這一模型較好地展示了高地形對實際熱液活動噴發位置的影響。

5.2 大西洋Lucky Strike 熱液區

Lucky Strike 熱液區位于慢速擴張（全擴張速率約為21mm/a[36]）的大西洋洋中脊37°17′N，是全球范圍內最大規模的熱液循環系統之一。受到其北東方向Azores 熱點的影響[37]，該熱液區范圍內發育大量玄武質熔巖[38]和明顯的高地形起伏，Lucky Strike 熱液區便位于區內較高的地形上（圖6a）。文獻[17]通過地震反射波速異常揭示了在Lucky Strike 熱液區下伏3km 的深度范圍內發育約4km 寬的透鏡狀巖漿部分熔融體，可認為其為維持上覆Lucky Strike 熱液對流系統運行的巖漿熱源。

基于Lucky Strike 熱液區的實際情況，我們將模型設置為10km×3km，高溫熱源（600℃，寬約4km）位于模型底界中央，對應實際的巖漿部分熔融體[17]。通過研究區跨軸水深分布計算得出對應的跨軸海水壓力剖面（圖6b），并將其設置為模型頂界的壓力邊界條件，其他邊界條件則保持不變。考慮到Lucky Strike 熱液區位于慢速擴張洋中脊的構造背景下，更加充分的洋中脊構造伸展作用使其洋殼滲透率較快速擴張環境明顯提升[39]，因此，我們賦予模型相對EPR 9°17′N 熱液模型更高的均一滲透率（約5×10?15m2）。將模型運行至100 ka 以確保其到達穩態。

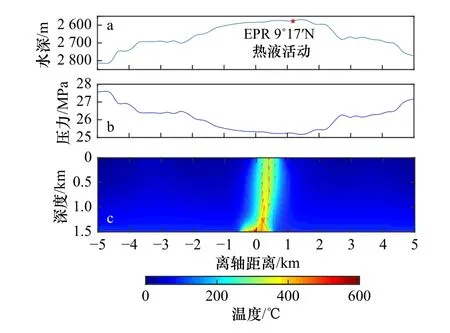
圖5 基于EPR 9°17′N 熱液區地形剖面的數值模擬結果Fig. 5 Simulation result based on the bathymetric profile of the EPR 9°17′N venta. EPR 9°17′N 熱液區跨軸剖面; b. 基于水深剖面計算的海水壓力剖面; c. 穩態數值模擬結果，離軸距離為0 代表洋脊軸的位置a. Cross-axis profile of EPR 9°17′N vent; b. calculated seawater pressure profile; c. running result in steady-state, distance=0means the location of ridge axis

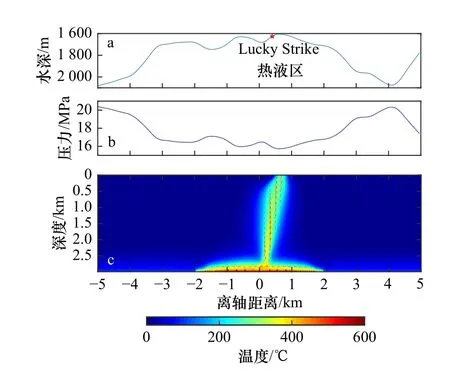
圖6 基于Lucky Strike 熱液區地形剖面的數值模擬結果Fig. 6 Simulation result based on the bathymetric profile of the Lucky Strike venta. Lucky Strike 熱液區跨軸剖面; b. 基于水深剖面計算的海水壓力剖面; c. 穩態數值模擬結果，離軸距離為0 代表洋脊軸的位置a. Cross-axis profile of Lucky Strike vent; b. calculated seawater pressure profile; c. running result in steady-state, distance = 0means the location of ridge axis

在穩態的數值模擬結果中，洋殼內部穩定發育一個規模相對較小（寬度約為500m）的高溫（約300℃）熱液羽，并發生約800m 的離軸偏移（圖6c），最終導致熱液海底噴發位置與Lucky Strike 熱液區的實際位置保持很好的吻合效果。因此，該模型可以較好地模擬出實際的Lucky Strike 熱液對流系統的形態和噴發位置。

5.3 對流模型的建立

基于上述地形起伏相關的熱液系統偏移程度的解析模型（圖4）和符合實際熱液系統的模擬結果（圖5，圖6），關于洋底地形起伏聚集上涌熱液流體的理論模型最終得以建立（圖7）。在該模型中，洋殼內部輝綠巖墻底界的透鏡狀巖漿熔融體作為上部新生洋殼的來源[3]和維持區內熱液循環系統的熱源，低地形部分及其下伏滲透性洋殼表現為主要的海水充注區域，而高地形由于上覆海水壓力的相對減小，使其成為熱液上升、釋放和噴發的主要匯集區域（圖7）。

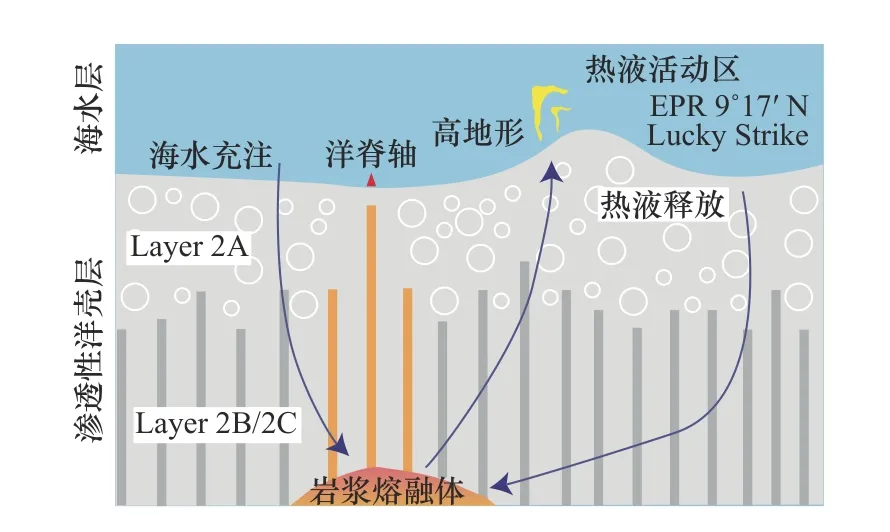
圖7 洋中脊高地形熱液噴發與對流模型Fig. 7 Convectionmodel for hydrothermal venting on bathymetric highs

6 結論

（1）基于達西流體充填的孔隙?彈性熱力學模型可以直觀、有效地模擬出不同環境下的洋殼內部熱液對流形態、溫度結構和熱液噴發位置等信息。

（2）結合數值模擬結果所獲得的解析模型可以定量地表現不同規模的洋底地形起伏對洋殼內部熱液對流形態的影響，且洋底高地形規模越大，地形起伏程度越大，下伏熱液羽向洋底高地形的偏移就越明顯。

（3）通過結合EPR 9°17′N 和Lucky Strike 熱液區實際的跨軸水深剖面，可以獲得與二者實際噴發位置相吻合的模擬結果，表明洋底高地形對下伏熱液羽的實際偏移影響。

（4）地形起伏相關的洋中脊熱液對流模型揭示洋底的平坦低地形及其下伏滲透性洋殼表現為主要的海水充注區域，而高地形由于上覆壓力的減小，使其成為匯集熱液釋放和噴發的主要區域。