基于啟發式搜索的浮點表達式設計空間探索方法

李 釗，董霄霄，黃程程，任崇廣

（山東理工大學計算機科學與技術學院，山東淄博 255000）

0 引言

隨著信號處理和圖像處理等在現場可編程門陣列（Field Programmable Gate Array，FPGA）上的廣泛應用，浮點計算在FPGA 上的應用變得越來越流行［1-4］。浮點數可以增加數據的表示范圍，但是浮點計算的誤差也會導致最終結果不準確。根據IEEE 754 標準，通過加、減或乘兩個浮點數產生的計算結果都應四舍五入為IEEE 754 浮點數格式，這種舍入是浮點計算不準確的原因。當浮點數格式固定的前提下，浮點計算的誤差主要取決于浮點表達式的形式。例如：表達式(x+y)2可表示為(x+y)×(x+y)和x×(x+y)+y×(x+y)等不同的形式，當x的取值范圍為[0，0.000 02]，y的取值范圍為[20，21]時，兩個表達式的表示范圍分別為[-5.53×10-5，5.53×10-5]和[-5.05×10-5，5.05×10-5]，從而產生不同的誤差［5］。

浮點計算在FPGA 平臺上實現時，若浮點數格式固定，資源消耗主要取決于浮點表達式的形式。例如：表達式(x+y)×(x+y)需要一個乘法器和兩個加法器，而表達式x(x+y)+y(x+y)需要兩個乘法器和三個加法器，表達式(x+y)×(x+y)消耗更少的資源。因此通過優化浮點表達式的結構，可實現資源消耗的優化。

浮點計算還需考慮計算時間，計算時間主要依賴于浮點運算器的流水線深度以及浮點表達式的形式。當浮點運算器確定的前提下，可以通過改變浮點表達式的形式來改變計算時間。例如：若采用相同的浮點運算器，表達式(x+y)×(x+y)可設計兩級流水線結構完成計算，而表達式x(x+y)+y(x+y)需要設計三級流水線結構完成計算，表達式(x+y)×(x+y)具有更短的計算時間。

一個浮點表達式經過因式分解和提取公因數等方法進行變形后可生成大量等價的浮點表達式，例如：x2+xz+z(x+y+z)+y(2x+y+z)可產生698 個等價表達式，每個表達式具有不同的計算精度，而且資源消耗和計算時間也不同。可采用浮點運算器的結構優化、指數和尾數位寬調節和等價表達式的設計空間探索等方法，實現浮點計算在FPGA 上的優化。

文獻［6］中采用半單元偏置格式設計浮點加法器和乘法器，以降低浮點運算器的資源消耗并提高計算速度。文獻［7］中提出了一種新的位對重編碼算法，該算法可有效減少浮點乘法運算中部分積行數，并減少與多路復用器、移位器和加法器相關聯的部分積的數量，與全精度乘法器相比可節省49%的面積和44.2%的功耗。文獻［8］中采用Newton-Raphson 迭代方法設計了一種32 位流水線浮點除法器，該除法器支持IEEE 754 標準中指定的所有類型的數據，該方案與現有方法相比需要多消耗30%的功耗，但所提出的流水線方法顯著降低了計算時間。文獻［5］中提出OptiFEX 優化框架，可根據數據輸入范圍和最大允許誤差等參數，調節浮點運算器指數和尾數的位寬，從而減少資源消耗，提高計算效率。

對浮點運算器進行優化，可減少運算器的資源消耗，并有效提高計算效率，但是浮點計算多為多個浮點數的混合運算，浮點表達式的結構也是制約浮點計算優化的關鍵。

文獻［9］中設置一組關于資源消耗、計算時間和精度的約束條件，并從等價表達式集合中選擇滿足約束的等價表達式，從而完成設計空間的探索。利用該方法選擇的表達式雖然滿足約束條件，但仍可能是可支配的，因此選擇的表達式不一定是最優表達式。文獻［10］中通過迭代分解的方法對初始浮點表達式進行變形，在迭代過程中采用Pareto 算法刪除非最優的表達式，從而減少等價表達式的數量，然后從剩余表達式中選擇資源消耗和計算時間最優的浮點表達式。該方法在探索過程中對可支配等價表達式及其后繼表達式進行了刪減，其探索過程不能覆蓋整個搜索空間，因此其選擇的非支配表達式的資源消耗、計算時間和精度等性能可能不是最優的。

針對上述問題，本文提出一種新的浮點表達式設計空間探索的方法，該方法不僅對非支配表達式的鄰域進行空間探索，同時對可支配列表中的表達式進行再次評估，選擇該列表中非支配表達式，并對其鄰域進行探索，最后再次對非支配列表中的等價表達式進行探索，得到最優的浮點表達式。該方法可對給定的浮點表達式及其等價表達式進行探索，探索過程基本覆蓋整個搜索空間，根據優化目標和約束條件選擇最優的等價表達式，因此不會引入浮點數處理的錯誤；同時該方法有效提高了非支配列表中非支配表達式的多樣性和隨機性，提高了最優表達式的性能指標。

1 產生等價表達式的方法

浮點表達式在等價變換過程中，以不同的等價表達式為起點，可能會重復出現同一個表達式，如圖1 中，表達式x(x+y)+y(x+y)重復出現兩次。若多次對同一個表達式進行性能評估會影響空間探索的效率。

圖1 浮點表達式變換示例Fig.1 Example for floating-point expression transformation

本文參考文獻［5］中的方法實現了等價表達式的變換。首先對初始表達式進行因式分解，直到表達式不能進一步分解，然后對分解后的表達式進行迭代提取公因式，直到沒有新的等價表達式產生。例如對(x+y)2的變換過程如圖2 所示，采用該方法可有效避免在等價變換過程中重復出現同一表達式。

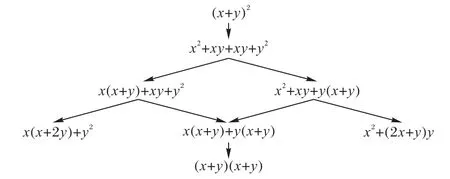
圖2 （x+y）2的等價變換過程Fig.2 Equivalent transformation process of（x+y）2

2 設計空間探索方法

設計空間探索是一個多目標優化過程，可實現多目標的折中［11-13］。為了提高設計空間探索的效率，需要根據優化目標，設計目標函數以及相關約束，并在設計空間探索過程中對每個設計個體的性能進行評估，判斷是否滿足目標函數。另外需要設計搜索算法，利用該算法選擇下一步要評估的個體，將設計空間引導到符合優化目標的區域。

2.1 優化目標函數

浮點表達式在設計空間探索過程中，會產生多個等價的表達式，表達式的精度、計算時間以及資源消耗等都會有所不同。設計空間探索的目的是依據優化目標，將設計空間引導到符合優化目標的區域。浮點表達式設計空間探索的優化目標函數如式（1）：

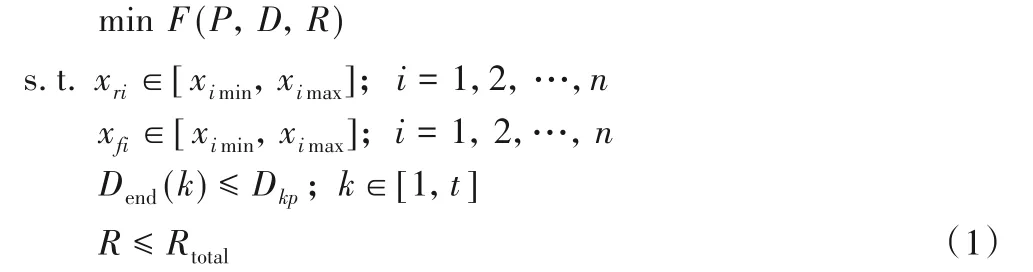
其中：P為浮點表達式的計算精度，可由式（2）計算得到，為表達式以更高指數和尾數長度表示的計算結果Fr(xr1，xr2，…，xrn)與當前參與空間探索的表達式的計算結果Ff(xf1，xf2，…，xfn)之差的絕對值，其值越小表示計算精度越高，例如當前參與計算的為IEEE754 標準的32 位浮點數，則采用IEEE754標準的64位浮點數作為參考數據。D為浮點表達式在FPGA 上實現后從輸入浮點數據到輸出計算結果的時間，由關鍵路徑上各處理單元的計算時間之和計算得到，如式（3）所示，m為關鍵路徑上處理單元的數量。R為FPGA 上實現浮點計算的資源消耗，由各個處理單元的資源消耗之和計算得到，如式（4）所示，t為浮點運算所需處理單元的數量。為了更好地實現多目標優化，對優化目標函數設置了多個約束條件，參考表達式的參數xri和參與計算表達式的參數xfi的取值必須在其允許的取值范圍內，關鍵路徑的計算時間Dkp應該大于等于任意處理單元的完成時間Dend(k)，任意處理單元的完成時間Dend(k)可由該處理單元的計算時間與該處理單元的前任處理單元的計算時間之和得到，如式（5）所示，其中d為前任處理單元的數量。最后浮點運算的資源消耗應小于等于FPGA平臺總的資源Rtotal。

2.2 啟發式搜索方法

浮點表達式在設計空間探索中會產生多個等價表達式，等價表達式之間的計算精度、資源消耗和計算時間等都有所不同［14-15］。每次迭代過程中采用啟發式搜索方法對產生的浮點表達式進行評估，提取非支配的浮點表達式作為局部最優的表達式，并以非支配表達式為起點進行新一輪的迭代。

2.2.1 非支配浮點表達式的定義

若e為一個浮點表達式，N為浮點表達式的集合，且e∈N，若e滿足式（6），則浮點表達式e為集合N中的非支配浮點表達式。

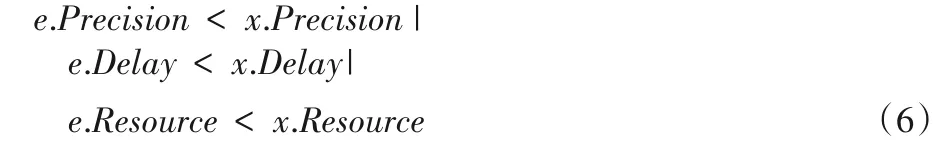
其中：?x∈N；Precision、Delay和Resource分別為表達式的計算精度、計算時間和資源消耗。

2.2.2 非支配浮點表達式的選擇

現有的方法在進行空間探索時，為了提高探索效率，直接刪除可支配表達式的后繼等價表達式，不對其進行評估，而后繼表達式中可能存在非支配解。為此，本文提出一種新的非支配浮點表達式的選擇方法，可覆蓋整個探索空間，算法流程如圖3所示。

1）首先將給定的需要探索的表達式進行因式分解，將分解后的表達式作為初始表達式。

2）然后對該表達式提取公因式進行等價變形，即得到初始表達式的鄰域，并計算鄰域中等價表達式的計算精度、計算時間和資源消耗等性能指標，得到非支配的等價表達式和可支配的等價表達式，并將可支配的表達式添加到可支配列表中，同時保存非支配表達式到非支配列表中。

3）以新的非支配表達式為起點，通過提取公因式得到相應的鄰域，并探索鄰域，最終得到該起點鄰域中的非支配的等價表達式和可支配的等價表達式，并分別添加到可支配列表和非支配列表中。

4）再次以新的非支配表達式為起點，按照步驟3）進行探索，直到達到規定的迭代次數或者無新的等價表達式產生。

5）上述過程未對可支配表達式的鄰域進行探索，該步驟首先對可支配列表中的表達式進行探索，提取該集合中的非支配表達式，并對其鄰域進行探索，將鄰域中的非支配表達式保存到非支配列表中，可提高非支配列表中多項式的隨機性和多樣性。

6）由于非支配列表中的表達式是在相應的鄰域內是非支配的，因此需要再次對非支配列表中的等價表達式進行探索，若該列表中存在可支配的表達式，則將其刪除，保留的等價表達式即為最終的最優浮點表達式。

圖3 浮點表達式空間探索算法流程Fig.3 Flowchart of floating-point expression space exploration

3 實驗驗證

為了驗證本文提出的基于啟發搜索的浮點表達式設計空間探索方法的有效性，將提出的空間探索方法與現有的針對浮點表達式空間探索的方法從計算精度、計算時間和資源消耗等方面進行對比分析。為了便于比較，選擇表達式結構由簡單到復雜的多個浮點表達式作為測試表達式，表達式中各參數的精度設定為：x∈[0.01，0.15]，y∈[0.32，0.43]，z∈[1.11，1.35]，指數的寬度設為5，尾數的寬度設為10，采用就近舍入方法。

為了更好地對計算精度進行評估，分別在設定的精度范圍內，均勻地取10 個浮點數據，首先分別按照IEEE754 標準格式對表達式進行計算，將該計算結果的均值作為參考的準確結果，然后按照實驗要求格式，對表達式進行計算，并計算實際結果的平均值，兩個平均值之差的絕對值即為計算精度。在設計空間探索過程中，利用FloPoCo［16］來提取加法器和乘法器的資源消耗和計算時間。FloPoCo 是一個用于生成算術數據通路的開源C++框架，其輸出是一個可綜合的VHDL代碼。

為了對各種設計空間探索方法的計算時間和資源消耗進行定性和直觀比較，分別從各種方法產生的非支配表達式集合中隨機選擇5個表達式在FPGA 平臺上進行仿真實驗驗證。FPGA 平臺選用Kintex7 系列的XC7K325T，綜合工具為Vivado2017.4，參考時鐘頻率為120 MHz。

實驗選擇3 個主流的浮點表達式設計空間探索方法進行對比分析，包括快速選擇空間探索（Fast Selection Design Space Exploration，FSDSE）方法［10］、基于迭代分解的空間探索（Design Space Exploration using Iterative Factorization，DSEIF）方法［9］和調節浮點運算器指數和尾數位寬自動調節的設計空間探索（Exploring Area-efficient with Optimized Exponent/mantissa Widths，EAOEW）方法［5］。

3.1 計算精度對比分析

表1 為不同的設計空間探索方法對不同表達式進行探索后，選擇的非支配表達式計算產生的計算精度對比。由表1可知，本文提出的浮點表達式設計空間探索方法的計算精度與DSEIF 方法相當，但是要優于FSDSE 和EAOEW 方法。例如針對浮點表達式(x+y+z)2，本文提出的方法的計算精度等于DSEIF 方法的計算精度，與EAOEW 方法相比本文提出方法的計算精度提高了9%，與FSDSE 方法相比提高了4%。主要原因在于DSEIF 方法是對整個搜索空間進行探索，分別對每個等價多項式進行計算精度等性能進行評估，并從中選擇非支配表達式，其缺點是空間探索效率低。FSDSE 為快速選擇空間探索方法，在探索過程中對可支配等價表達式及其后繼表達式進行了刪減，其探索過程不能覆蓋整個搜索空間，而可支配表達式的后繼節點中可能存在計算精度更高的表達式，因此其選擇的非支配表達式的計算精度會降低。EAOEW方法在空間探索過程中，只對資源消耗進行評估，所以其計算精度最低。本文提出的方法采用啟發式搜索，在避免對可支配表達式進行探索的同時，盡可能地覆蓋整個搜索空間，提高了最終選擇非支配表達式的多樣性和隨機性，從而保證了計算精度的準確性。

表1 四種方法的計算精度對比Tab.1 Calculation accuracy comparison of four methods

3.2 計算時間對比分析

圖4 為針對每個測試表達式隨機選擇的5 個最優等價表達式計算時間的平均值。計算時間為將經過設計空間探索后得到的最優表達式在FPGA 平臺上運行所需要的時間。從圖4 中可知，本文提出的空間探索方法得到的非支配表達式的計算時間與DSEIF 方法相當，要優于FSDSE 和EAOEW 方法，例如針對表達式x(x+2z)+y(y+2x)+z(z+2y)，與FSDSE方法相比本文提出方法的計算時間減少了5%，與EAOEW 方法相比減少了12%，本文方法可選擇計算時間更優的等價表達式。主要原因在于本文方法不僅對非支配表達式的鄰域進行探索，同時選擇可支配列表中的非支配表達式，并對其鄰域進行探索；還對最終產生的非支配列表再次進行探索，最終得到最優的等價表達式，從而提高了選擇計算時間最優的表達式的概率。

圖4 四種方法的計算時間對比Fig.4 Calculation time comparison of four methods

3.3 資源消耗對比分析

圖5 為針對每個測試表達式隨機選擇的5 個等價表達式資源消耗的平均值。從圖5 中可知，與計算時間不同，EAOEW 方法具有最優的資源消耗，本文提出的空間探索方法得到的非支配表達式的資源消耗與DSEIF 方法相當，要優于FSDSE 方法，例如針對表達式y(x+y)2，與FSDSE 方法相比，本文提出方法的資源消耗減少了5%。主要原因是：在設計空間探索過程中，EAOEW 只針對資源消耗一個性能進行評估，選擇的等價表達式是資源消耗最優的；而本文方法是針對計算精度、計算時間與資源消耗三個性能進行綜合評估的，為三個性能的折中優化。

圖5 四種方法的資源消耗對比Fig.5 Resource consumption comparison of four methods

3.4 設計空間探索時間對比分析

因為本文方法與DSEIF 方法在計算精度、計算時間與資源消耗等方面性能相當，為進一步對比兩種設計空間探索方法，用設計空間探索的時間對二者進行對比分析。設計空間探索時間是指在PC平臺上，利用浮點表達式設計空間探索方法對等價的浮點表達式及其鄰域進行探索，直到得到最優表達式所需要的時間，可體現設計空間探索方法的效率。

圖6 為兩種設計空間探索方法對不同表達式進行探索的時間對比。本文提出方法的設計空間探索時間要優于DSEIF方法，尤其當浮點表達式結構復雜時，其時間優勢越明顯，例如對表達式x(x+2z)+y(y+2x)+z(z+2y)，本文提出方法的空間探索時間比DSEIF 方法縮短了89 s。主要原因是：DSEIF 方法需要對整個設計空間進行探索，探索效率低；而本文方法在保證對非支配表達式的鄰域進行探索的前提下，對可支配列表中的表達式進行選擇性的探索，在保證覆蓋整個搜索空間的同時，有效提高了設計空間探索的效率。

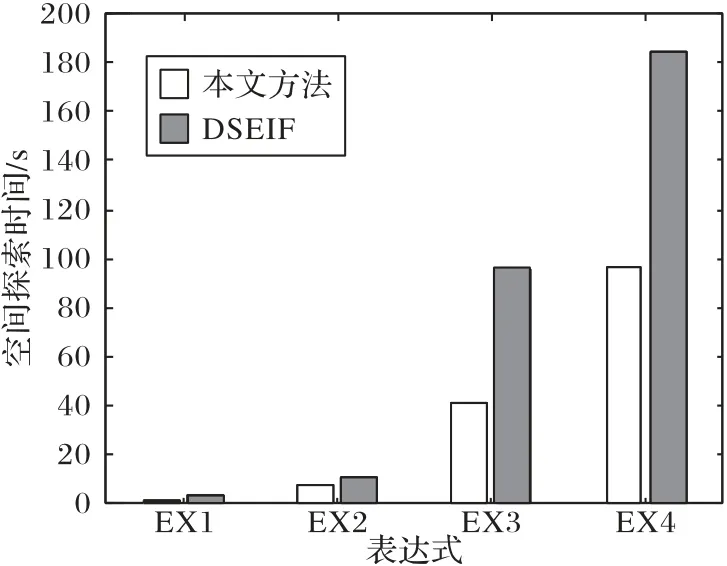
圖6 設計空間探索時間對比Fig.6 Design space exploration time comparison

4 結語

本文對浮點表達式設計空間探索的問題進行研究，針對已有的方法空間探索效率低下和計算性能差等問題，提出一種基于啟發搜索的浮點表達式設計空間探索方法，并與現有的具有代表性的浮點表達式設計空間探索方法對典型的浮點表達式進行實驗對比，實驗結果表明本文提出的浮點表達式設計空間探索方法，在有效提高空間探索效率的前提下，得到的等價表達式具有更高的計算精度、更低的計算時間和資源消耗。