抽水蓄能機組不穩定現象的流動機理與控制方法

羅先武 ，葉維祥 ，楊丹丹 ，冉紅娟

（1.清華大學二氧化碳減排與資源化利用技術北京市重點實驗室，北京市 100084；2.清華大學水沙科學與水利水電工程國家重點實驗室，北京市 100084；3.上海交通大學機械與動力工程學院，上海市 200240）

0 引言

由圖1所示的2018年中國能源構成可知，超過2/3的電量仍然來自燃煤發電[1]，這給中國實現溫室氣體減排、減少大氣污染等社會發展目標帶來巨大壓力。而近年來風力發電、光伏發電等可再生能源得到高速發展，在電力市場中所占據的比例逐年提升，又使得中國電力系統的穩定性面臨嚴峻的挑戰。為此，大力發展水電，尤其是大容量抽水蓄能，增強整個電力系統的快速調節能力是解決目前中國電力生產矛盾的重要策略。因而發展高水頭抽水蓄能技術，不斷提升在負荷快速轉換期間的機組穩定性、保證抽水蓄能電站應對電力負荷快速轉換能力是至關重要的。

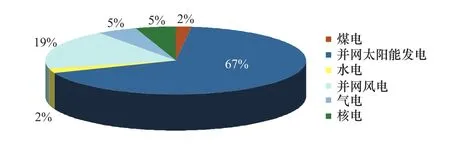
圖1 中國發電量比例Figure 1 Ratios of different power generation in China

圖2列舉了自20世紀60年代以來國內外抽水蓄能電站的設計水頭分布[2]，充分說明了現代抽水蓄能技術不斷朝著高水頭、大容量方向發展的趨勢。中國近期建成或在建的大型抽水蓄能電站水頭也大都超過了500m。高水頭抽水蓄能技術不僅對電站機組結構提出了更高的要求，而且更加強調機組在偏離設計負荷工況下的運行質量。已有研究表明，當運行在偏離設計工況時，抽水蓄能機組內部往往出現非定常不穩定的流動現象，如作為水輪機運行的發電工況下存在旋轉失速[3]；而在偏低負荷泵工況時抽水蓄能機組易發生強烈的水壓脈動，水壓脈動可誘發間歇性空化[4]，而不均勻的壓力脈動引起轉輪的徑向力波動、轉子動力學不穩定[5]，嚴重時導致機組強烈振動[6]、葉片裂紋或轉輪上冠斷裂[7]。通常情況下，抽水蓄能機組在泵工況下的非穩定性問題較水輪機工況更嚴重，有時甚至威脅到機組與電站的安全性。所以，抽水蓄能機組泵工況的非穩定流動特性及其機理是水電設備行業長期的熱點研究方向。

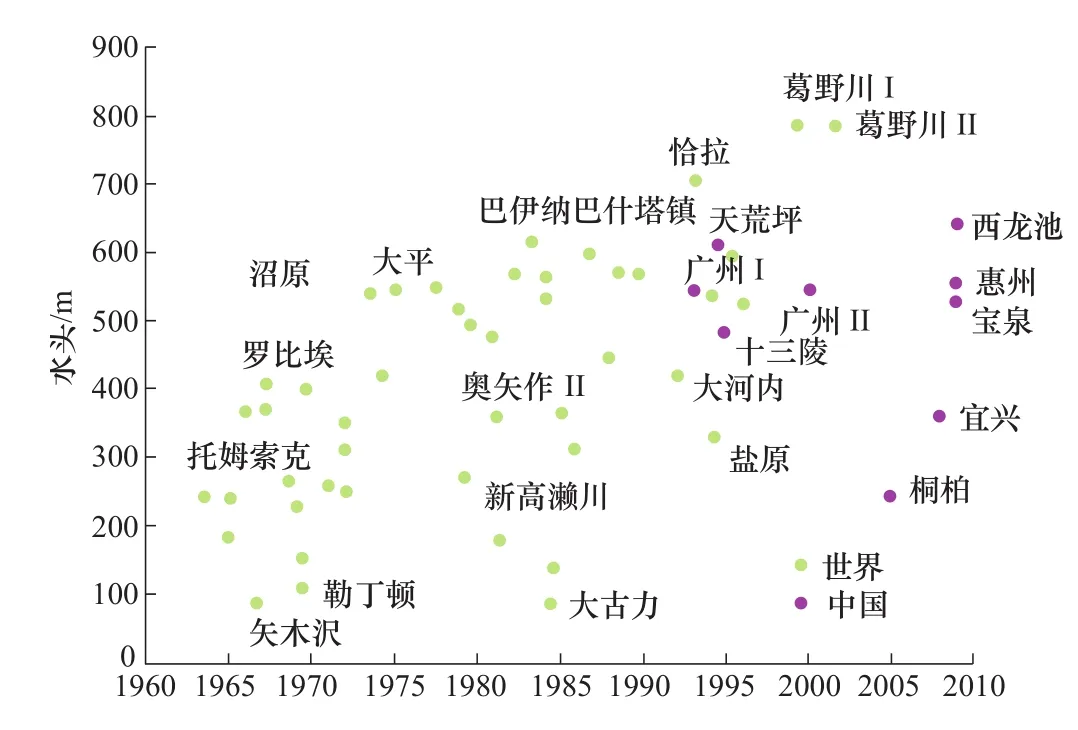
圖2 抽水蓄能電站水頭變化趨勢[2]Figure 2 Pumping head variations for pumped storage power-stations[2]

抽水蓄能機組泵工況下的強烈水壓脈動源自轉輪與活動導葉之間的動靜干涉。活動導葉進口靠近轉輪下環側發展的強漩渦引發相鄰導葉流道內的逆流，使得導葉流道中的流動經歷通暢—堵塞—逆流—堵塞—通暢的周期性循環過程[8]；而在周期性循環過程中由于流道被堵塞導致導葉內水力損失急劇增大，進而體現為性能曲線或特性曲線的駝峰[7]。由于性能曲線或特性曲線的駝峰是水力旋轉機械內部流動不穩定的外在表現，所以通過研究內部不穩定流動機理進而提出抑制駝峰的工程策略是未來進一步發展抽水蓄能技術的必然途徑。盡管針對駝峰現象的研究歷史可追溯至20世紀70年代，但仍需深入梳理已有研究數據以清晰揭示抽水蓄能機組泵工況下的不穩定流動特性，并基于機組內部流動的基本特性確定合理的工程措施來抑制駝峰現象、從而增強機組的運行穩定性。

1 抽水蓄能機組不穩定特性的預測

1.1 泵工況不穩定特性

圖3表示通過模型試驗測得的抽水蓄能機組某開度下泵工況的特性曲線[9]。橫坐標表示無量綱化流量，數值為運行流量與最優效率點流量（QBEP）之比；縱坐標為無量綱化揚程，為運行揚程與最優效率點揚程的比值。結果表明特性曲線在0.70QBEP、0.90QBEP附近分別都出現駝峰，這兩處駝峰在圖中分別以PS1、PS2表示；兩種記號“*”“o”分別對應試驗中不同流量調節方向的工況點，記號的大小表征相應工況下測得的壓力脈動幅值。由圖3中的結果可知，沿著不同流量調節方向進行試驗時駝峰出現的流量范圍及對應的壓力脈動都有所不同，這種現象稱為“現象”。但在圖3所示的結果中，兩種不同流量調節方向對應的遲滯現象并不顯著；無論是從小流量至大流量方向還是從大流量朝小流量方向變化，駝峰PS2工況（如B點）的壓力脈動均比駝峰PS1工況的壓力脈動更強烈。

對于圖3所示的特性曲線駝峰，其中PS1對應的流量較大，可稱為高部分負荷駝峰；而PS2對應的流量較小，按照習慣可稱為部分負荷駝峰。所以，在泵工況下抽水蓄能機組中出現部分負荷駝峰時水壓脈動更強，而流量調節方向并不改變這一性質。

對于駝峰PS1，特性曲線波峰對應的工況點約為0.91QBEP，特性曲線谷底對應的工況點約為0.87QBEP（以試驗中特性曲線明顯不穩定的流量下降方向為主要參照工況）。在模型試驗中，在駝峰PS1附近所有工況下皆能捕捉到頻率為0.2fn（fn：轉輪旋轉頻率）的水壓脈動分量。相比之下，特性曲線波峰處（即圖中A1點）的壓力脈動幅值較小，而特性曲線谷底處（圖中A2點）的壓力脈動強烈。

對于駝峰PS2，特性曲線波峰對應的工況點約為0.71QBEP（即圖中B1點），特性曲線谷底對應的工況點約為0.68QBEP（圖中B2點）。在模型試驗中，特性曲線波峰工況時可以觀察到轉輪葉片進口的片狀空泡，而特性曲線谷底工況時可以觀察到轉輪葉片進口附近的間歇性漩渦。由于機組內部的流動比較復雜，駝峰PS2附近的壓力脈動頻率不規則，可捕捉到0.14fn、0.8fn等多種復雜成分[10]。所以，在部分負荷駝峰工況下空化、漩渦與大規模流動分離團等非穩定現象及其耦合作用導致了機組內部激增的水力損失與強烈的壓力脈動。

圖3 抽水蓄能機組泵工況特性曲線的駝峰Figure 3 Positive slope at characteristic curve for pumped storage unit at pump mode

1.2 不穩定特性的數值預測方法

由于特性曲線駝峰屬于水力機械內流不穩定的外在體現，主導該現象的內在流動機理則需要通過計算流體力學方法進行分析。因而，為適應工程應用的需求，在抽水蓄能機組設計階段就準確模擬機組的內部流動，進而預測泵工況的不穩定特性具有十分重要的實際意義。

目前常用RANS（reynolds-averaged navier-stokes，雷諾平均納維—斯托克斯）方法來預測抽水蓄能機組實際運行中的不穩定特性。實踐證明，RANS方法雖然可能部分捕捉泵工況下的不穩定特性，但仍存在解析精度不足的問題。圖4用空心圓記號表示基于k-ωSST湍流模型計算的揚程系數[11]。與實驗數據（圖中以實心方塊記號表示）相比，采用RANS方法預測的揚程系數變化趨勢與試驗結果并不一致，尤其在駝峰處的預測誤差較大，說明基于RANS方法預估的泵工況特性還不能滿足實際工程的要求。為了提高計算精度，已有研究嘗試將LES（large eddy simulation，大渦模擬）方法應用于抽水蓄能機組的不穩定特性預測。為了開展LES計算，將抽水蓄能模型機組（轉輪外徑為523.5mm）內部流動的雷諾數降低25倍、采用8.5×107個網格單元進行了大渦模擬。圖5給出了LES、RANS兩種方法預測的結果與模型試驗的對比，表明大渦模擬可以比較準確地預測特性曲線駝峰位置的流量系數，以及機組內旋轉失速團的傳播速度，這些計算數據均接近模型試驗得出的數據[12]。根據圖5（b）可以推論，采用LES方法比URANS（unsteady RANS，非定常RANS）方法預測抽水蓄能機組泵工況非穩定特性具有明顯的優勢。

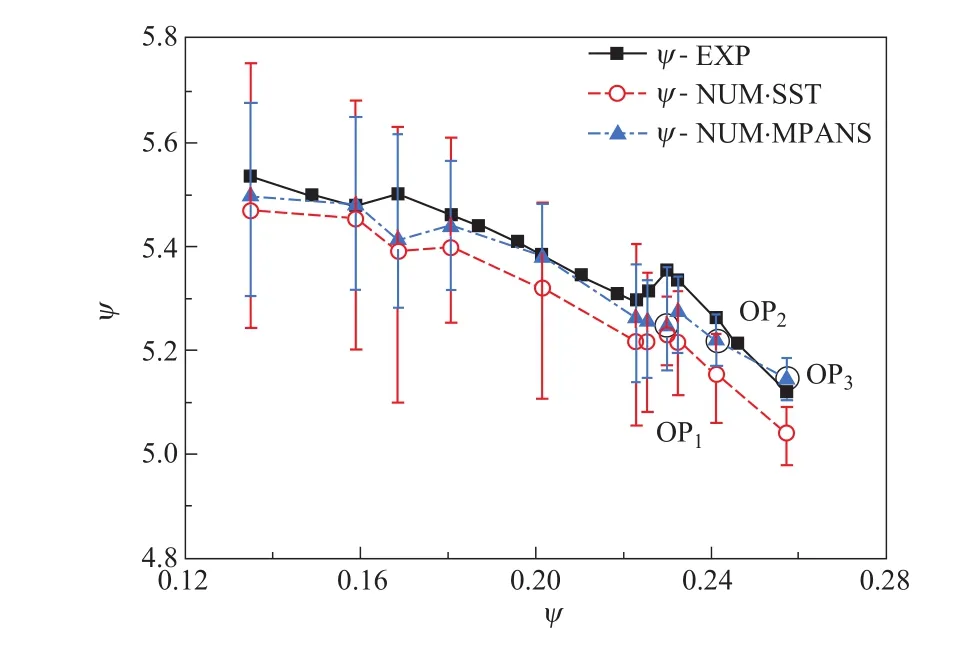
圖4 抽水蓄能機組泵工況不穩定特性[11]Figure 4 Unstable characteristics for pumped storage unit at pump mode[11]

即使大渦模擬的預測精度較好，但由于計算成本過高，要開展抽水蓄能機組不穩定特性的LES分析還很困難。在圖5中，僅對模型機組特性曲線的一個工況點（圖中工況點Ⅲ）進行了大渦模擬，而且還須降低雷諾數以適應計算中的硬件資源。由此可見，在短期內大渦模擬尚不能全面用于抽水蓄能技術研究，尤其難以直接用于抽水蓄能原型與模型機組的不穩定特性分析。因此，為了促進中國抽水蓄能技術健康發展，有必要研究一種合理匹配預測精度與計算資源需求的不穩定流動特性數值模擬方法。

1.3 動態PANS模擬方法

在圖4中，除了URANS模擬數據之外，還給出了基于PANS（partially averaged navier-stokes）方法預測的結果。圖中“MPANS”表示一種改進的動態PANS方法[13]。PANS方法是一種介于DNS（direct numerical simulation，直接數值模擬）與RANS之間的橋接模型，根據模型系數的動態變化，可使PANS兼具DNS在復雜流動區域的精細模擬與RANS模擬主流的快捷模擬兩種優勢。

對于不可壓縮非定常流動，動量守恒方程如下：

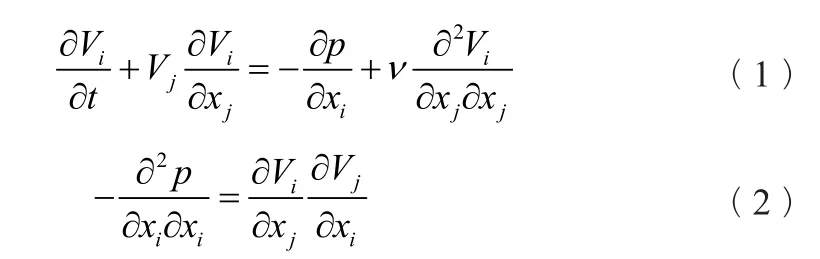
式中：p——壓力；

ν——運動黏性；

Vi、Vj——沿i、j方向的速度，Vi由求解的速度分量Ui和未求解速度分量ui組成，即：

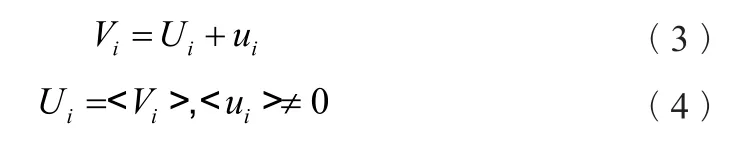
式中：< >為部分平均操作符。

部分平均的Navier-Stokes方程可表示為

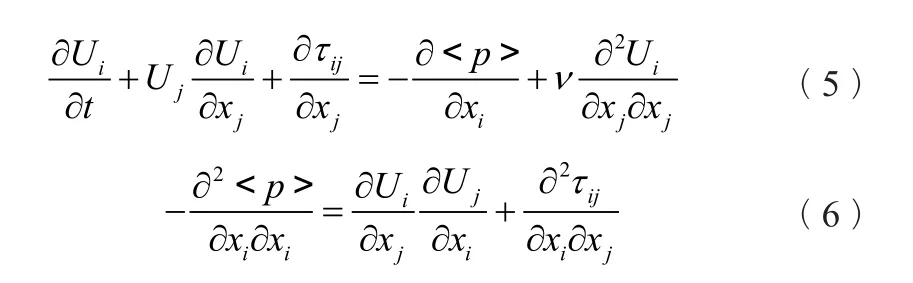
式中：τij類似于RANS方法中的雷諾應力與LES中的亞格子應力，τij= - ，須通過一定的湍流模式求解。

基于標準k-ε湍流模型的動態PANS模型為

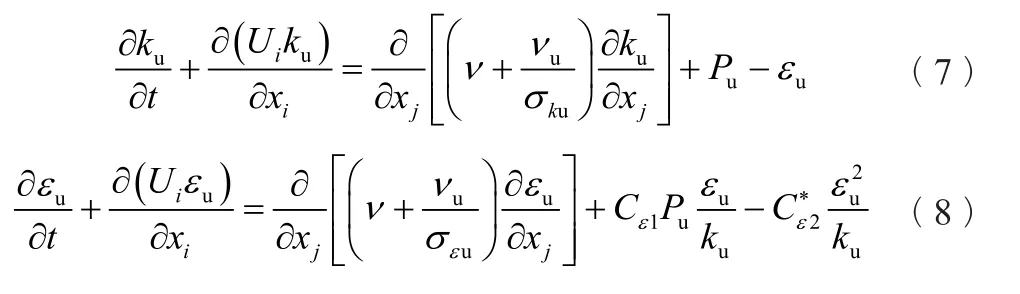
式中：u——未求解量；

k——湍動能；

ε——湍動能耗散率；

νu——；

P——湍動能生成項。

模型系數Cε1=1.44、Cε2=1.92、σk=1.0、σε=1.3，其他系數可由下式求出：

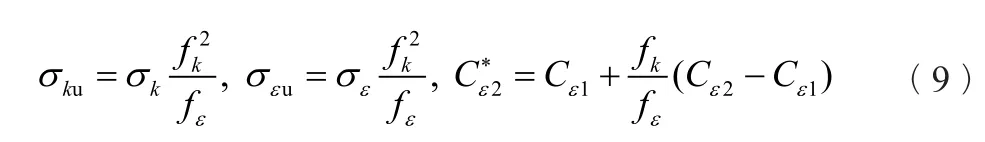
式（9）包含兩個系數fk，fε。其中fk為未求解的湍動能ku與全部湍動能k之比，fε為未求解的湍動能耗散率εu與湍動能耗散率ε之比。這兩個系數可按照公式（10）計算：

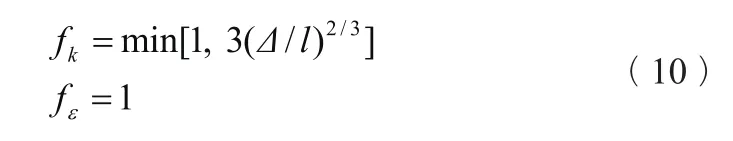
式中：l——混合湍流尺度，l=k1.5/ε；

Δ——局部網格尺度，l=（ΔxΔyΔz）1/3。

由式（10）可知，任意質點處的fk取決于流場中混合湍流長度與局部網格尺度。所以，動態PANS模型屬于一種依據流場特性自動調整模型參數的湍流模擬方法。

圖4的結果表明，與傳統的RANS方法相比，采用動態PANS模型的數值計算過程相對穩定，揚程系數的變動范圍比較小，由動態PANS預測的揚程變化趨勢和試驗測量結果基本一致，而駝峰OP1處的揚程更接近試驗值。

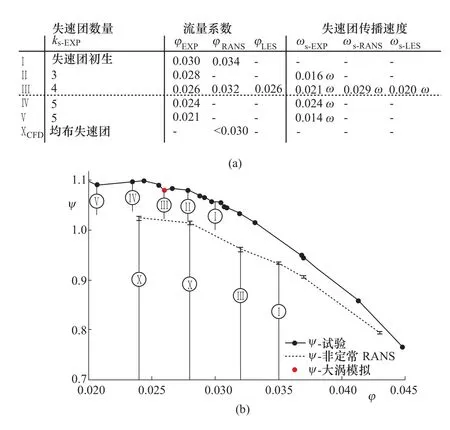
圖5 計算結果與試驗數據的對比[12]Figure 5 Comparisons for numerical simulation and experimental data[12]

隨著研究的不斷深入，針對基于標準k-ε湍流模型的動態PANS模型，提出了不同修正策略的PANS方法。如文獻[14]中構建了一種考慮流道曲率與旋轉效應的新PANS方法，該方法用于模擬小流量工況下離心式葉輪內部非定常流動，更細致地揭示了性能曲線駝峰對應的葉輪內不穩定漩渦演化[15]。改進后的PANS方法可以更有針對性地解決實際流動的精細化模擬問題，從而為解決工程問題提供更有價值的指導。

2 機組內部流動不穩定機理

2.1 不穩定工況下的內部流場特征

圖6表示泵工況的特性曲線及三種部分流量工況下葉輪內的平均流動[16]，其中圖6（b）為PIV試驗結果，圖6（c）為基于動態PANS模型的計算結果。在外特性方面，采用動態PANS模型能較好地預測泵工況的特性曲線，尤其是駝峰附近波峰與谷底之間的揚程變化趨勢；在內流方面，采用動態PANS模型的數值模擬基本復現了PIV試驗中捕捉的葉片間流道內大規模流動分離及漩渦。PIV試驗與數值模擬的結果均顯示了在部分流量工況下葉輪中平均流動的復雜性：在φ=0.5φbep與φ=0.6φbep兩種工況下，在所有葉片間流道內都出現了較大尺度的流動分離，而這些分離團不僅出現在葉片吸力面，也出現在葉片壓力面，它們對葉輪內的主流形成了一定的阻塞效果。如φ=0.5φbep時，在葉片間流道A、B、C中的阻塞效果特別顯著，而在葉片間流道D、E內的阻塞效果相對較輕；在φ=0.78φbep時，流動分離團的尺度相對較小，且主要出現在葉片吸力面靠近葉輪外徑處。此時流動分離對主流的影響相對較小。

圖7表示抽水蓄能模型機組泵工況下不同時刻活動導葉內的流速分布[12]。圖7（f）給出了14個轉輪旋轉周期內，流經兩個活動導葉之間的流量變化曲線，流量測量斷面位于活動導葉GVA與GVB之間，即圖7（a）中的紅色斷面。圖7（b）中，活動導葉GVA與GVB之間的流動暢通，此時對應最大的流量；而圖7（d）中，源自GVB吸力面的流動分離逐漸擴大，并基本占據了活動導葉GVA與GVB之間的流道，使得流速矢量都轉向切線方向，此時由于流道的堵塞，通過GVA與GVB之間的流量急劇下降，接近了最小流量。流道的嚴重堵塞將直接導致水力損失的激增，是抽水蓄能機組泵工況下出現特性曲線駝峰的根源。

由圖7（f）可知，駝峰工況下活動導葉中的不穩定流動引起流動分離并逐漸阻塞流道；通過導葉間流道的流量呈周期性變化。這種周期性變化的流動誘發強烈的水壓脈動。圖8表示在轉輪出口至活動導葉之間的無葉區所監測的水壓脈動。在圖8（a）中，實線為瞬時壓力脈動，而虛線表示是以轉輪旋轉頻率fn為限的低通濾波曲線。由圖8（b）所示的結果可知，除了轉輪葉片（轉輪有9個葉片）通過頻率9fn的脈動成分，及其2倍諧頻（18fn）成分之外，壓力脈動還包括一個明顯的低頻成分，其頻率僅為轉輪旋轉頻率fn的7.6%。總體上，圖8中的三種壓力脈動成分都屬于旋轉的轉輪與靜止部件之間動靜干涉的結果，但它們的原理卻不同：轉輪葉片通過頻率及其2倍諧頻的兩種壓力脈動分量都是抽水蓄能機組結構引起的，即轉輪的旋轉葉片與導葉、蝸殼等靜止流道直接干涉的結果；而7.6%fn的低頻壓力脈動分量雖然也源自結構干涉，但該壓力脈動則反映了由于結構干涉誘發不穩定流動的影響，可以看成是一種間接的干涉效果。

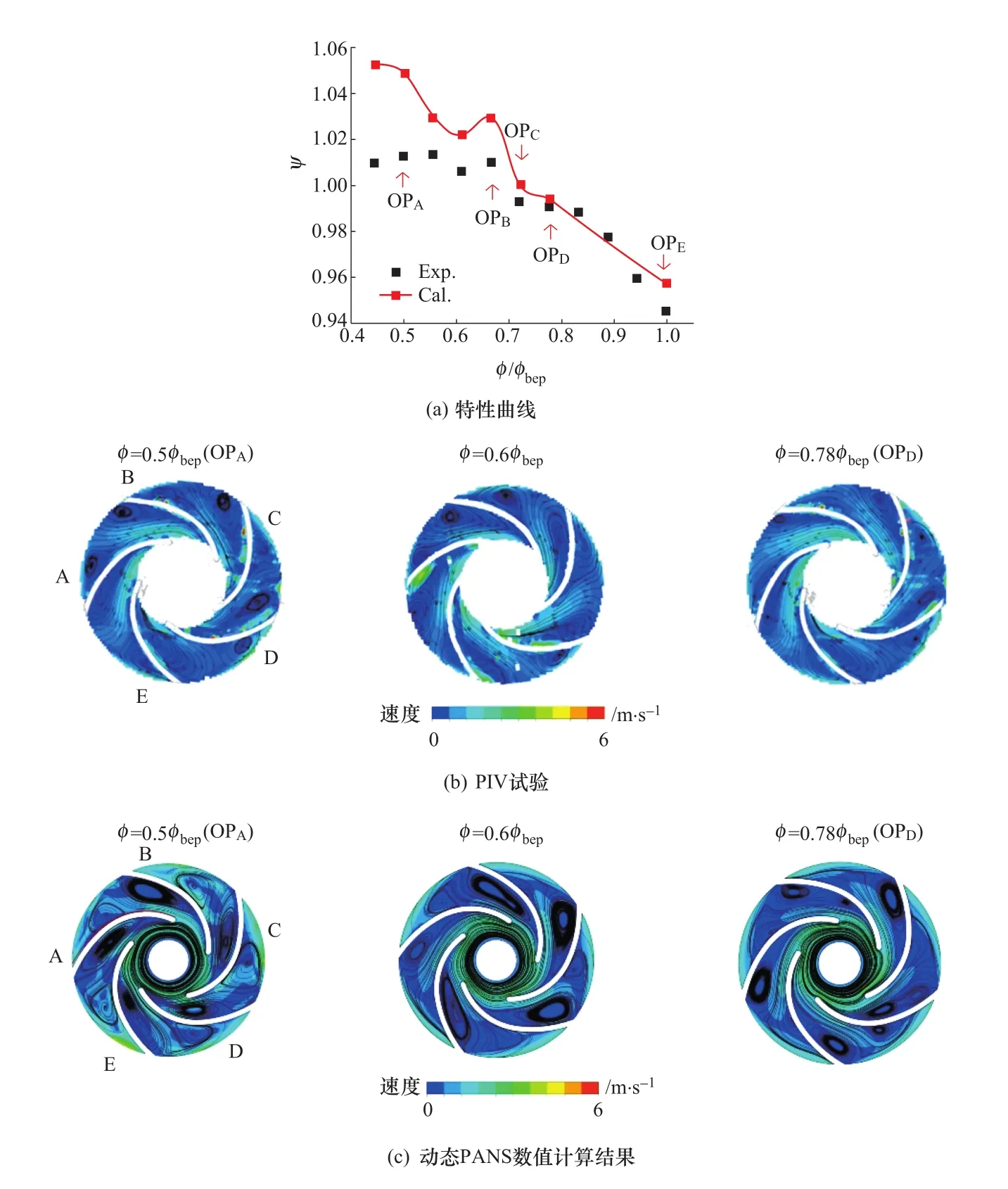
圖6 部分負荷工況下葉輪中的平均流動[16]Figure 6 Averaged flows in pump impeller at part load operations[16]

2.2 不穩定流動結構的傳播

在圖7（f）中，流經導葉GVA與GVB之間的流量隨時間呈現周期性變化。由于流量變化，必定引起導葉進口處的流速大小與方向發生變化，這樣在活動導葉進口發生了液流沖角的急劇變化。在圖4的結果基礎上，圖9中顯示了無葉區不同位置處水流沖角AOA的變化；其中橫坐標采用了以角度表示的無葉區相對位置，縱坐標為水流沖角AOA。三種工況OP1、OP2、OP3分別對應抽水蓄能模型機組泵工況下的駝峰點、高部分負荷點及最優效率點，如圖4所示。當機組運行在最優效率點OP3時，水流沖角AOA盡管隨時間波動，但變化幅值較小；而當機組運行在駝峰工況OP1時，水流沖角不僅隨著時間變化，而且在同一時刻沿周向不同位置處的水流沖角也出現了劇烈變動，其中在約80°、200°和320°的周向位置出現了沖角峰值，這些峰值對應著發生不穩定流動的典型區域。為了清晰展現轉輪至導葉之間的不穩定流動，圖10（a）中顯示了兩條參考線，其中“line 1”靠近活動導葉進口，而“line 2”則靠近轉輪外徑。圖10（b）的結果表明，在駝峰工況點（OP1）轉輪外徑處的水流角α沿“line 2”分布很不均勻，在葉片出口附近水流角甚至接近零，而在θ=112°處的水流角則將近20°。這種不均勻出流對活動導葉進口附近的流動產生了重要影響，使得AOA沿“line 1”的分布出現大幅度變化，如在θ=85°處水流沖角達17.5°，而在θ=115°處沖角為-2.5°。由圖10（a）中的速度矢量可知，此時不同導葉之間流道內的流動狀態具有顯著差異，如導葉A與導葉B之間流道內出現了回流，導葉B與導葉C之間的進口基本被封閉、流道被堵塞，而導葉C與導葉D之間流道則完全通暢，流速很大。

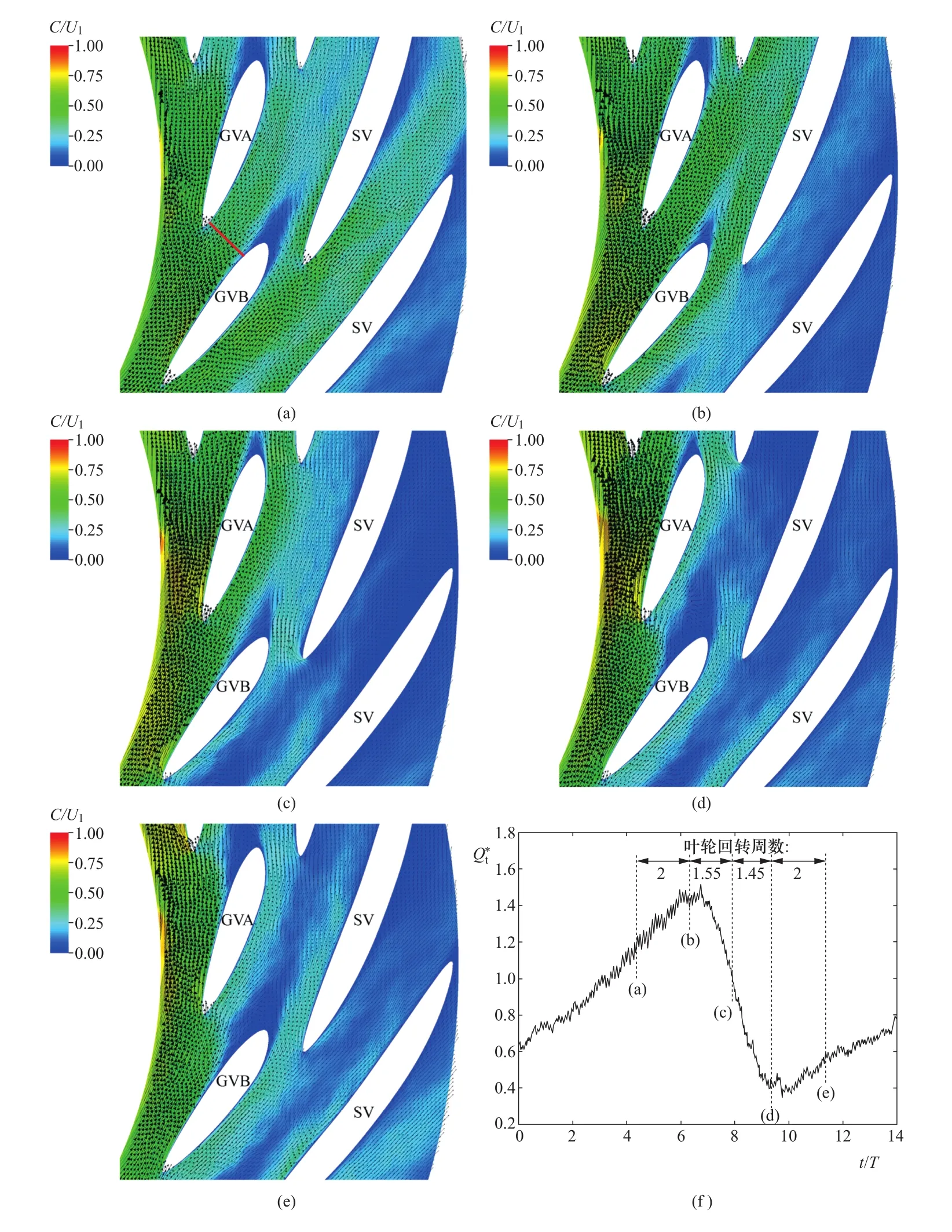
圖7 駝峰工況下活動導葉內的流速分布[12]Figure 7 Instantaneous flows in guide vanes at positive slope condition[12]

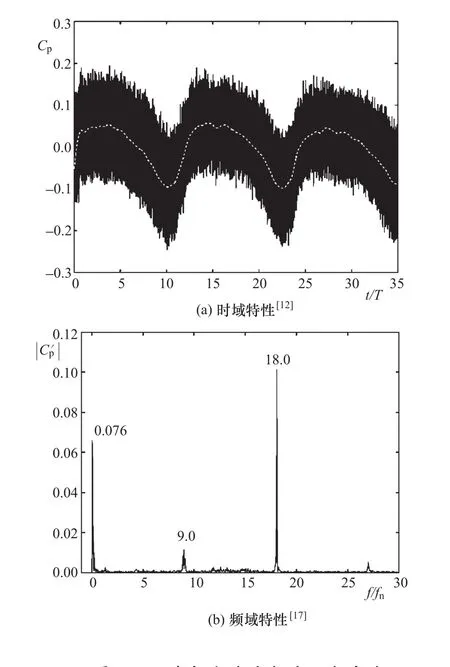
圖8 不穩定流動誘發的壓力脈動Figure 8 Pressure oscillations induced by unstable flow

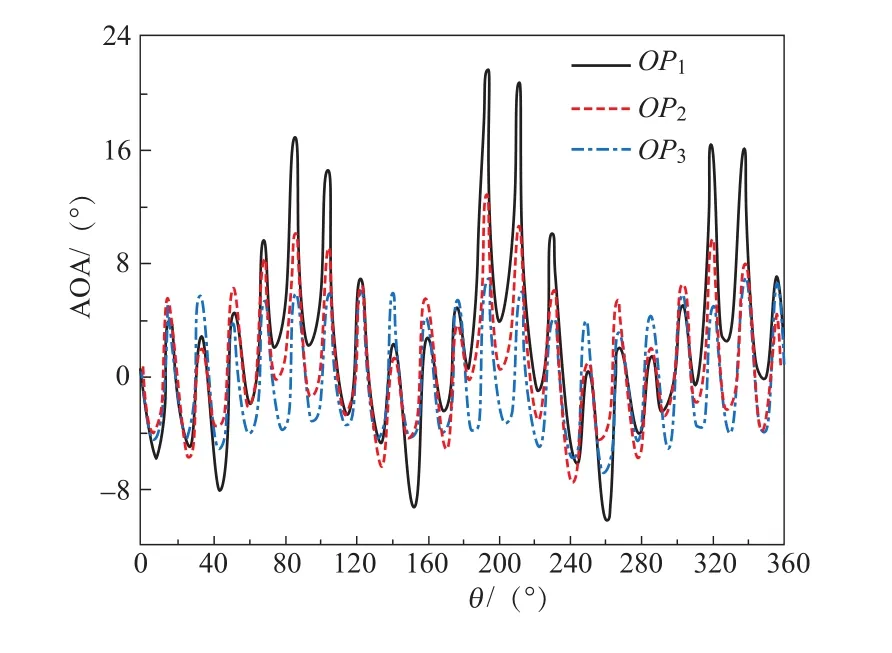
圖9 三種工況下活動導葉進口的沖角變化[11]Figure 9 Attack of angle at leading edge of guide vane at three operations[11]

事實上，即使在駝峰工況，這種導葉間流道內的“回流—堵塞—通暢”周期性流動特征并非在抽水蓄能機組靜止部件的全域中出現。在刻畫了駝峰工況（OP1）機組內不穩定流動的圖11（a）中，出現了3組不穩定流動結構（虛線框內），而且同時發生在活動導葉與固定導葉中。這種不穩定流動結構涉及流道的堵塞，通常可稱為“失速團”（stall cell）。由圖9可知，三組失速團之間的相位差約為120°；在部分負荷工況（OP2），機組內流動得到很大改善，盡管在導葉附近的局部位置出現了輕微流動分離，但流道內的流動比較穩定；在最優效率點OP3，機組靜止部件中的速度均勻性好，流動穩定，僅在靠近蝸殼隔舌的固定導葉中有極輕微的流動分離[11]。

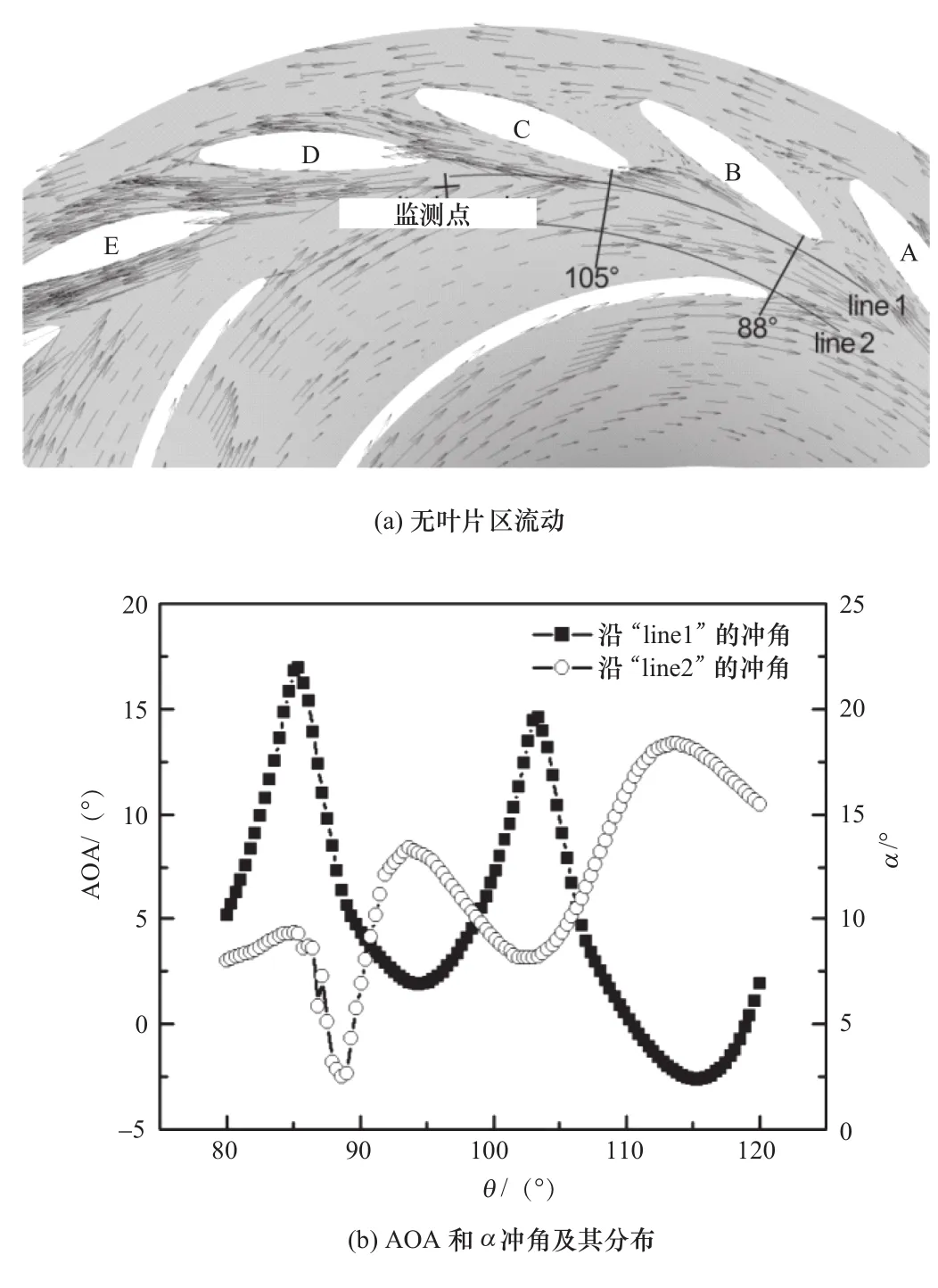
圖10 OP1工況下無葉區流動的變化[11]Figure 10 Flow angle distribution at vaneless area at OP1 condition[11]

如圖12所示，由逆流—堵塞—射流（指相鄰導葉間流道中通過的流量超過導葉間流道的平均流量）組成了抽水蓄能機組泵工況的不穩定流動結構，即失速團。由于失速團一般隨時間在機組內部流場中傳播，所以也被稱為旋轉失速團（rotating stall cell）。通常情況下，失速團的傳播頻率低于轉輪旋轉頻率fn。大量研究表明在流道中失速團的數量、傳播速率均與運行工況密切相關，可以通過監測無葉區壓力或者流場可視化試驗確定[18]。在離最優效率點Qbep較近的高部分負荷工況下，流道中的失速團數量較少，一般為1～3個；隨著流量繼續下降，失速團數量增多，如圖5所示。

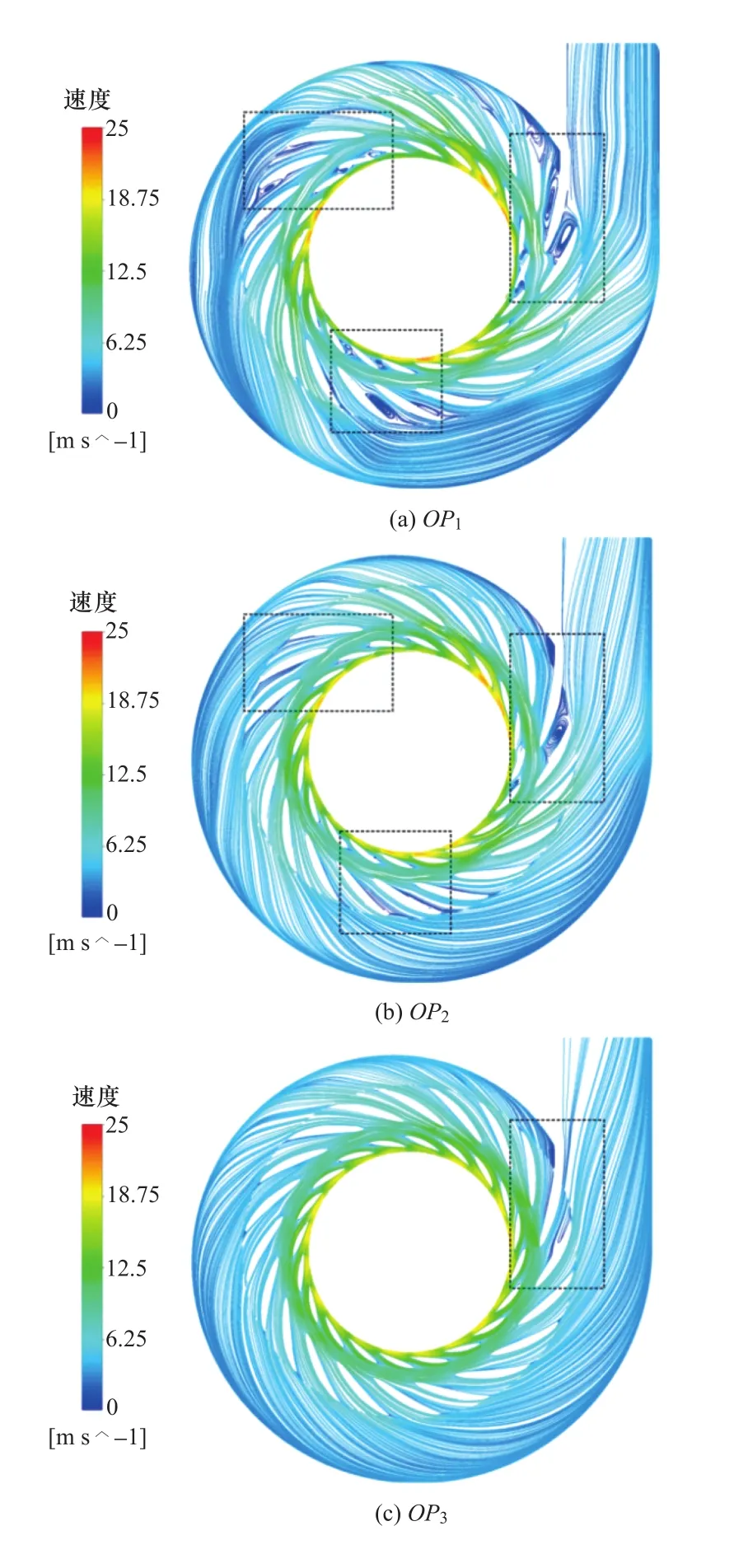
圖11 三種工況下機組靜止部件內的流動[11]Figure 11 Flow in unit stationary components at three operations[11]

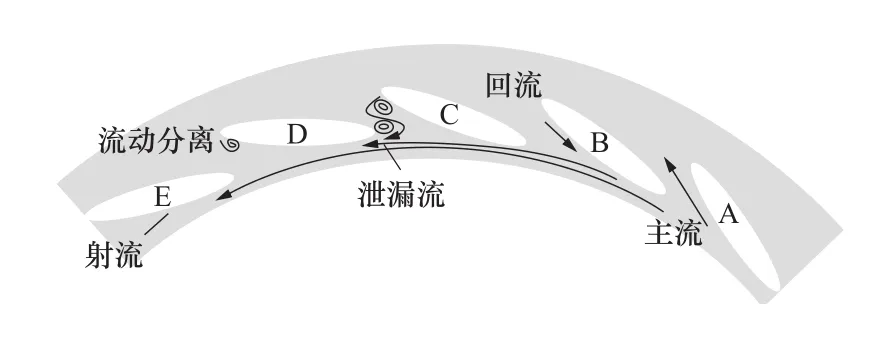
圖12 導葉內不穩定流動的傳播機制[11]Figure 12 Unstable flow propagation in guide vanes[11]

圖13給出了泵工況下不同運行流量所對應的失速團傳播速率比值[17]。圖13中，Ω為轉輪旋轉速率；Ωrs為失速團的傳播速率，可通過測量導葉進口處壓力脈動波形并進行快速傅里葉變換得出。圖13所示的試驗結果中，當流量系數φ在0.042～0.087范圍內變化時，流道內僅存在1個失速團。當φ=0.087時，壓力脈動顯著，噪聲達75.5dB（A），失速團沿葉輪旋轉方向傳播速率為0.083fn；而流量系數φ小于0.042時，流道內存在2個失速團。當φ=0.042時，試驗中測得的噪聲降低至72.8dB（A），失速團沿葉輪旋轉方向傳播速率為0.0665fn。當流道中只有單個失速團時，失速團的傳播速率可以直接通過流道中監測的壓力脈動頻率來確定；而當流道中存在n個失速團時，所對應的壓力脈動頻率是失速團傳播頻率的n倍。

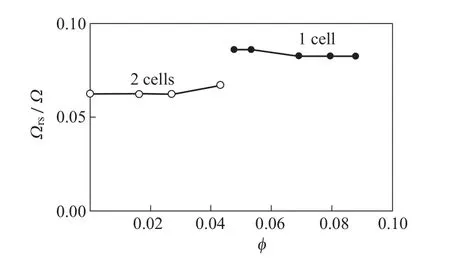
圖13 流道內失速團的傳播速率[19]Figure 13 Propagation speed of rotating stall in pump impeller[19]

失速團傳播速率Ωrs可由下列計算式[20]求出：

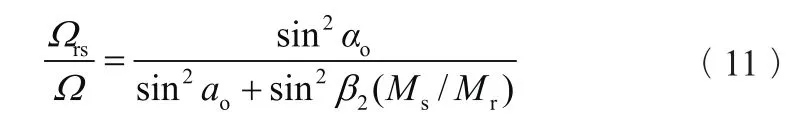
式中：Ω——轉輪旋轉角速度；

α0——導葉開度；

β2——轉輪外徑處的葉片安放角；

Ms——活動導葉與固定導葉中的流體質量；

Mr——轉輪內的流體質量。

使用式（11）可以預估失速團在流道中的傳播速率，可以為結構設計中避免機組共振提供一定的技術參考。

2.3 特性曲線駝峰的形成機制

抽水蓄能機組泵工況下，偏負荷運行條件易導致在葉輪出口的非均衡出流，進而由于動靜干涉作用在導葉內誘發不穩定流動。在流量較小時，不穩定特性主要受大尺度分離流動、進口預旋等因素影響；而隨著流量增大，流動分離的區域發生遷移，形成在導葉流道中傳播的失速團。失速團的傳播引起相鄰流道的堵塞、逆流與射流，誘發顯著的水力損失與水壓脈動。

采用局部熵產率（local entropy production rate，LEPR）可以表征內部流動引起的能量損失。圖14給出了開度為19mm、流量為0.74Qbep工況下轉輪葉片四個不同展向流道內的局部熵產率與流線分布[21]。圖中，“Dec”“Inc”分別表示逐步減小與逐步增大的流量變化方向。圖中的結果表明，轉輪內一旦發生了流動分離，尤其在葉緣附近有強烈的分離，就會出現很大的局部熵產率；對于不同的流量變化方向，葉輪中的流動有相似性，但同時也存在一定差異。圖15給出了開度為19mm、不同流量工況下，尾水管（圖中以“DT”表示）、葉輪（RN）、導葉（GVSV）和蝸殼（SP）中由熵產率轉化的流動損失[22]。由此可知，偏低負荷工況下的機組損失中，導葉與葉輪的損失較大。而當運行流量小于0.8Qbep時，導葉中的損失將大于葉輪內的損失。如圖14對應工況的流量為0.74Qbep，此時導葉中的損失接近4m，大于其他流動部件中的損失。

圖15的結果也表明，無論哪種工況，轉輪與導葉中的損失均較大。當機組運行流量大于0.9Qbep時，各種流動部件中的損失變化很小；而當運行流量小于0.8Qbep時，導葉、葉輪和尾水管中的損失同時急劇增大，使得機組水力損失遽然增大，導致泵工況的揚程陡降，這樣在揚程—流量曲線出現揚程谷底現象，即性能曲線上的駝峰。

圖14 不同展向轉輪流道的局部熵產率與流線分布[21]Figure 14 Local entropy production rate and streamline distribution at different spanwise flow passages[21]

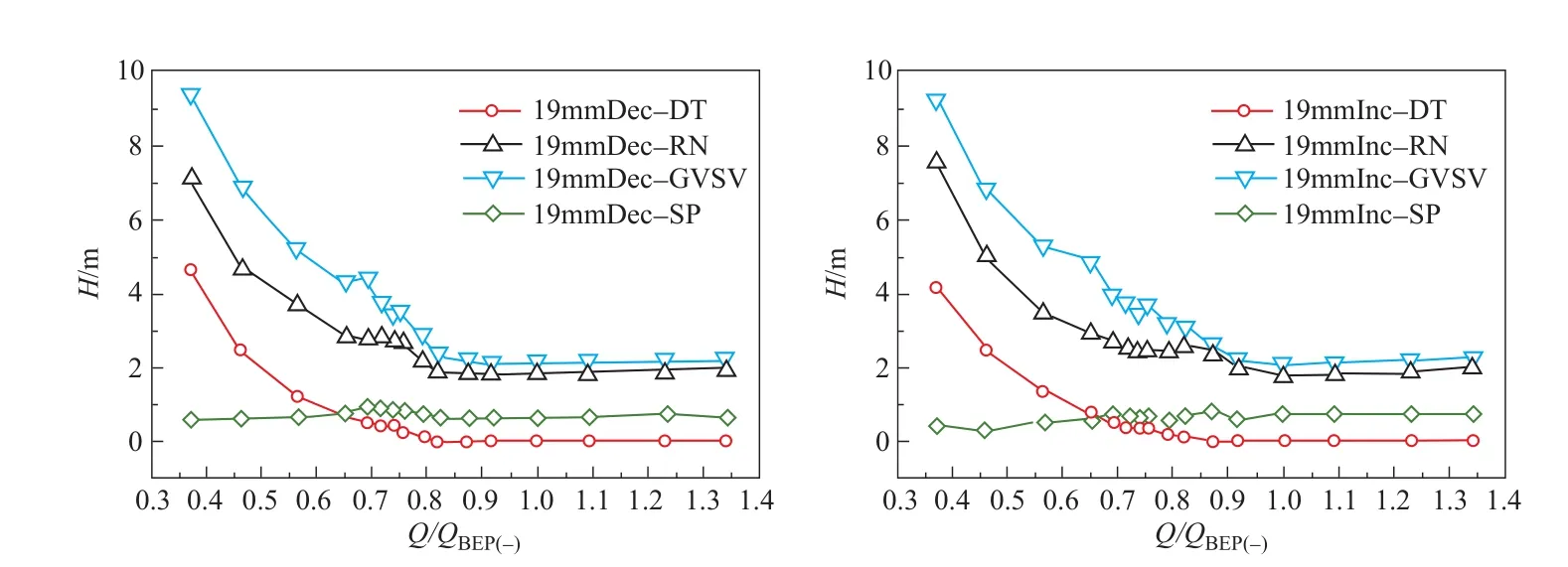
圖15 主要流動部件的損失[21]Figure 15 Head loss due to entropy production and flow discharge at different flow passages[21]

3 機組不穩定特性的控制方法

不穩定流動可導致強烈的水壓脈動，成為抽水蓄能機組安全運行的嚴重隱患。為了緩解抽水蓄能機組泵工況下的不穩定流動，在工程上可以從很多方面進行優化與控制[2]，包括優化轉輪設計，調整導葉開度、轉輪與導葉的間距、轉輪葉片安放角與包角，采用非同步導葉、長短葉片活動導葉、長短葉片轉輪，以及在流場特定位置引入射流等。

3.1 轉輪優化

轉輪是抽水蓄能機組的能量轉換單元，決定了泵工況下活動導葉之前的流動狀態，所以轉輪設計對特性曲線有重要影響。實踐證明，設計非規則的葉片出口角分布規律[10]、采用長短葉片[23]，以及改變低壓邊形狀[24]等措施都可能改善或消除特性曲線駝峰，并適當提高機組的效率。從動靜干涉的角度分析，優化轉輪的設計對于抑制機組內部不穩定流動的重要性是不言而喻的。

圖16是針對某抽水蓄能電站可逆式機組的兩種轉輪設計方案所對應的軸面流道輪廓圖[25]。在第一種設計方案（圖中Optimized A）的基礎上，通過改變上冠（Hub）與葉片低壓邊（LP）曲線，擴大了轉輪軸面流道所圍成的面積以及低壓邊的流道截面，并基于反問題設計、試驗設計法（DOE）、響應面法（RSM）、遺傳算法等構建的優化設計方法進行葉片形狀優化，設計新的轉輪模型為圖中Optimized B。圖17比較了兩種設計方案的模型轉輪。從轉輪低壓邊觀察，Optimized A轉輪的葉片朝正方向傾斜，而Optimized B轉輪的葉片則朝負方向傾斜。

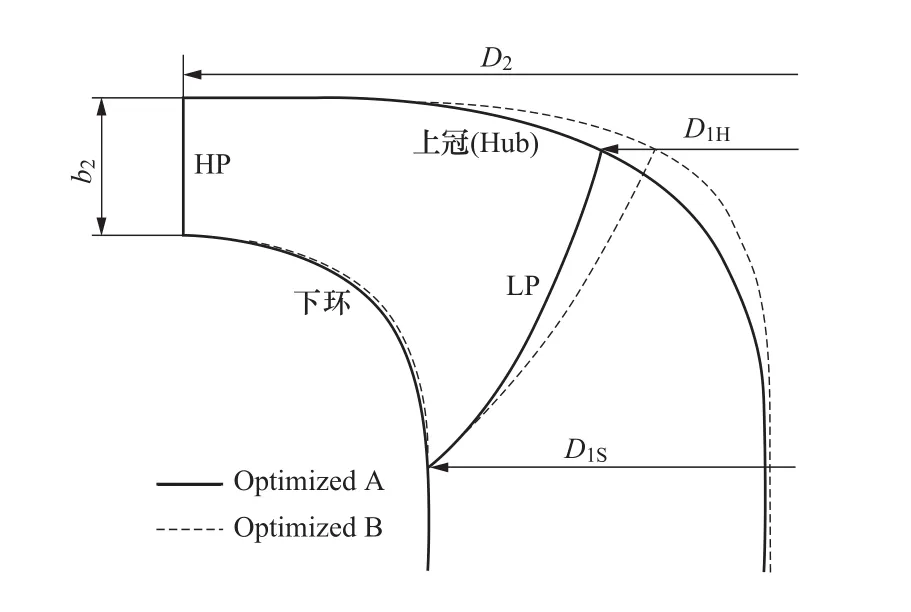
圖16 可逆式轉輪兩種設計方案的軸面流道輪廓[25]Figure 16 Meridional sections of two design schemes for pumped storage unit runner[25]

圖17 兩種不同設計方案的可逆式轉輪模型[25]Figure 17 Model runners of two design schemes for pumped storage unit runner[25]

圖18為兩種設計方案轉輪模型的試驗結果。在泵工況下，優化后的Optimized B轉輪的模型機組性能得到明顯改善：①基本消除了流量—揚程曲線的駝峰，避免了低負荷時的不穩定現象；②明顯提高了低負荷工況的機組效率，且模型機組的最高效率略有增大，接近92%。

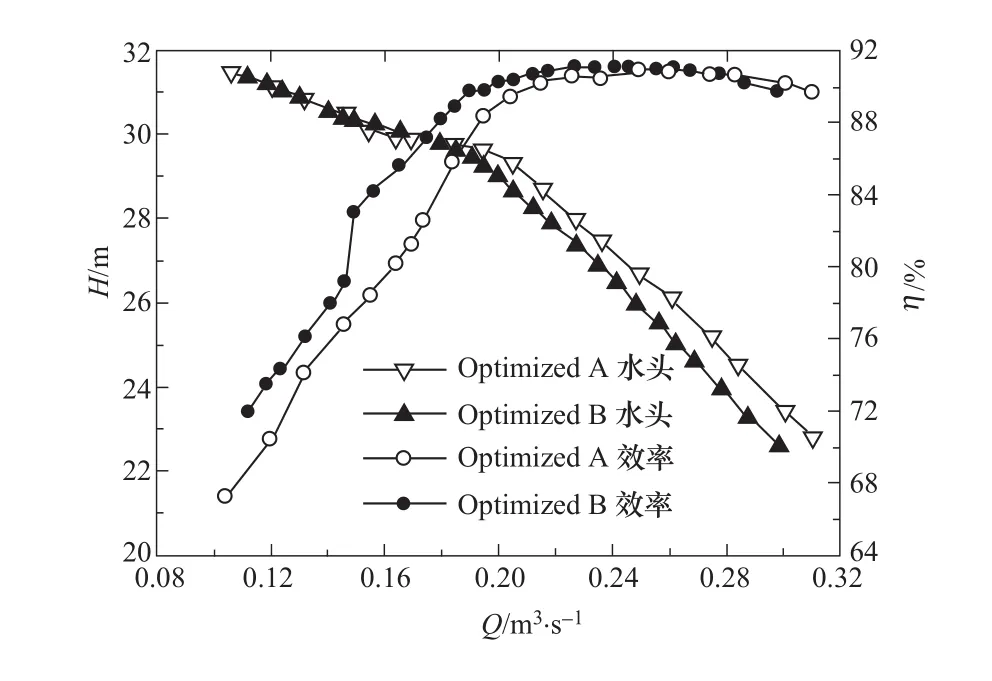
圖18 兩種可逆式轉輪的機組性能曲線[25]Figure 18 Hydraulic performance comparison for two pumped storage unit runner[25]

3.2 非同步導葉或異形導葉

由圖15可知，導葉中的損失較大，尤其在偏低負荷工況下損失可能劇增，從而導致性能曲線駝峰。因此，導葉的設計以及導葉在機組中的布置方式都能影響抽水蓄能機組的內部流動，進而造成機組的不穩定性能。

為保證抽水蓄能機組的穩定運行，目前工程中常用預開導葉的方法，即在小開度下預先開啟若干導葉至指定開度來緩解機組內部流動的不穩定性[26]，而預開導葉方案需要通過研究進行優化配置。圖19表示抽水蓄能機組中水力部件布置的示意圖。當四個導葉（圖中gv3、gv4、gv13、gv14）的開度保持一致，且大于其他活動導葉的開度時，機組內部壓力脈動發生變化。在靜止部件中的壓力脈動得到較明顯抑制，但轉輪中的壓力脈動有所增強[27]。需要指出，采用非同步導葉開啟方式在一些工況下可以改善機組內部流動與動靜干涉引起的壓力脈動，但不利于設計工況下形成軸對稱流動條件。因而，無論是采用非同步開啟導葉，還是設計非對稱分布的導葉，都需要統籌考慮在全運行區域下的機組性能。

研究還表明導葉高度對抽水蓄能機組內不穩定流動造成的動靜干涉及轉輪應力有一定影響。如針對某500m水頭級抽水蓄能機組，將導葉高度增大約40%，可使水輪機工況下的主應力降低20%～30%[28]，改善了機組的運行安全性。

近年來，基于仿生學原理設計的導葉在抽水蓄能機組中得到應用[29]，如采用不同波浪形導葉頭緣來抑制特性曲線駝峰。在選擇合理的凸起高度（2A）、展向波長（λ）時，可以在維持機組運行效率不變的前提下緩解內流的不穩定，降低在偏低負荷工況下的流動損失（見圖20）。

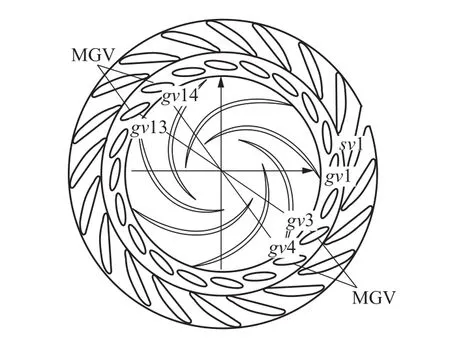
圖19 可逆式機組非同步導葉分布方案[27]Figure 19 Distribution scheme of misaligned guide vanes for pumped storage unit[27]

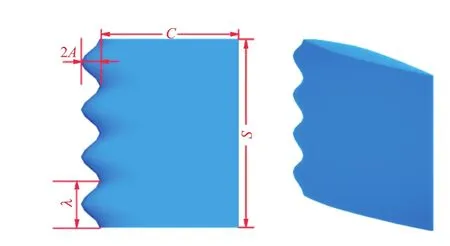
圖20 曲線形頭部的導葉[29]Figure 20 Guide vane with leading-edge protuberance[29]

3.3 導葉關閉/開啟規律

大量的工程經驗說明，合理的導葉關閉/開啟規律是保證抽水蓄能機組安全與電站穩定運行的必要條件。一般建議采用導葉開度分階段開啟方式，使得在導葉開啟過程中每個階段的水壓和軸功率波動幅度均較小且能夠很快衰減，確保機組穩定運行，并盡量減小電機功率突變對電網的沖擊[30]。

為了獲得最優的導葉關閉/開啟規律，需要對每個關閉/開啟階段的參數進一步優化。圖21對比了兩種不同的調節方案。基于NSGA-II遺傳算法的多目標優化方法確定兩段式導葉關閉曲線，并合理調整調壓井與水庫之間的距離，可使抽水蓄能電站最大超壓量減小4.2%，最大超速減小 7.1%[31]。

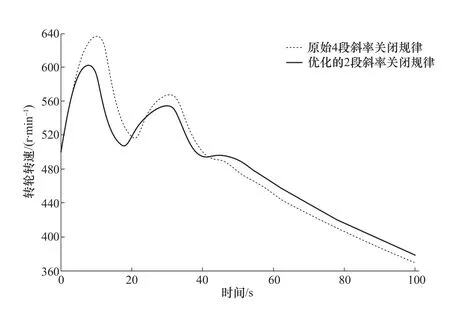
圖21 兩種不同導葉關閉曲線[31]Figure 21 Two curves for guide vanes closing[31]

4 結語

截至2018年底，中國抽水蓄能電站在運裝機容量達3002.5萬kW，在建抽水蓄能電站裝機容量約4321萬kW，在運、在建裝機容量均已穩居世界第一位[32]。隨著中國能源戰略實施與能源結構進一步優化，抽水蓄能在電力系統中將發揮巨大作用，未來還會得到迅速發展。因而，不斷研發先進的抽水蓄能技術、穩步推進中國抽水蓄能電站建設勢在必行。

抽水蓄能機組泵工況不穩定特性具有極其復雜的物理機制。經過多年研究，人們已部分理解駝峰工況下機組內部不流動特性，以及造成損失劇增的機理，進而采取相應的工程措施來改善機組的穩定性。盡管如此，目前對抽水蓄能機組不穩定流動機理并未達到全面、清晰而系統的認識，而無論是數值模擬還是試驗手段都存在精度不足的問題，亟待通過大量深入的工作以不斷改進研究方法，為解決抽水蓄能機組不穩定的工程實踐提供技術支撐。