在線學習神經網絡用于空調負荷預測研究

沈俊杰 龔延風 劉偉

南京工業大學城建學院

0 引言

空調負荷預測是冷水機組運行的基礎條件，是冷凍站控制策略制定的必要依據。目前，基于歷史統計數據的空調負荷預測技術發展比較成熟，方法主要有支持向量機法，神經網絡法，回歸分析法和時間序列分析法等[1]。但是這些預測方法都需要大量的歷史空調負荷數據，需要建筑建成后運行較長時間才能應用這些方法工作，導致了新建建筑建成運行初期難以進行負荷預測。同時對于一些既有建筑，由于歷史負荷數據不充足、記錄不完整或缺乏歷史數據，也影響了負荷預測方法在既有建筑節能改造中的推廣使用。

新建建筑建成運行初期和既有建筑缺乏歷史負荷數據時均稱為小樣本條件。為了解決小樣本條件下空調負荷預測問題，擴大負荷預測的使用范圍，提高冷凍站智能化運行的水平，本文提出了一種機理計算與神經網絡學習相結合的在線負荷預測方法。結合暖通空調專業的已有成果和統計學習兩者的優勢建立適用于小樣本條件的在線負荷預測流程，以求在建筑運行期間隨著實際負荷數據的逐步增加，通過在線學習逐步完善BP 神經網絡性能，快速建立小樣本建筑的空調負荷預測模型。

1 在線負荷預測流程的建立

在小樣本條件下，前期負荷預測可以依靠估算模型進行工作，并結合人的控制經驗輔助其進行評判分析，但主要仍以估算負荷為控制依據，以實現冷水機組臺數的實際控制。與此同時，通過測量供回水溫差和流量可以得到建筑的實際逐時冷負荷，該數據將成為樣本供BP 神經網絡在后臺試訓。在持續的試訓過程中，神經網絡的性能將逐步得到完善，最終可以投入使用。基于此的方案的小樣本條件下的負荷預測流程，如圖1 所示。

圖1 小樣本條件下的負荷預測流程圖

當神經網絡試訓結束后投入使用，此時用神經網絡模型取代估算模型，并結合人的控制經驗對冷水機組臺數進行實際控制。為了防止預測值在后續運行中出現較大誤差，仍需將負荷實際值與預測值進行比較。當負荷預測值和實際值的誤差滿足要求時，保持原模型不變。未滿足要求時，將負荷實際值繼續加入神經網絡模型，對模型進行修正完善。后期穩定運行時的負荷預測流程圖如圖2 所示。

圖2 后期穩定運行時負荷預測流程圖

2 負荷估算模型

2.1 負荷估算方法

基于空調負荷機理的估算模型如下：

式中：Q1為通過圍護結構得熱量形成的冷負荷，可采用冷負荷系數法求得，分為通過墻體、屋頂和窗戶瞬變傳熱形成的冷負荷和通過窗戶日射得熱形成的冷負荷，W；Q2為通過室內熱濕源散熱散濕形成的冷負荷，包括設備，照明和人體的得熱，W；Q3為新風冷負荷，W。

Q1的計算難點在于通過墻體，屋頂和窗戶的傳熱冷負荷計算。目前常用的負荷計算方法主要分為兩類。一類是基于設計條件的動態負荷計算方法，如諧波反應法、反應系數法、Z 傳遞函數法等。由于現有研究成果都是計算在設計條件下的空調負荷，尚無法直接應用到實際氣候條件下的動態負荷。另一類是針對季節或年度負荷的計算方法，如：如度日法、當量滿負荷運行時間法、負荷頻率法等，不能用來進行逐時負荷預測。空調負荷的估算面對實際不斷變化的室外氣象條件，本文提出基于動態負荷修正模型。

2.2 基于動態負荷的修正模型

因為此模型主要用于小樣本條件下的負荷預測，所以預測值精度要求可適度放寬。基于此并考慮到估算模型的簡便易算，決定將通過墻體，屋頂和窗戶的瞬變傳熱冷負荷采用其逐時得熱量進行替代。

2.2.1 通過墻體，屋頂和窗戶的得熱量的修正

通過墻體、屋頂的得熱量：

式中：K 為圍護結構傳熱系數，W/(m2·K)；F 為墻體或屋頂的面積為室外綜合溫度的平均值，可以根據天氣預報的最低最高氣溫以及太陽輻射強度計算得出，℃；tN為室內空氣溫度，℃；υ 為外墻對綜合溫度擾量的衰減度，由于外墻結構已定，可通過計算獲得；Δtz為實際逐時綜合溫度與全天綜合溫度的差值。

通過窗戶的瞬變傳熱得熱量：

式中：F 為窗戶的面積，m2；tw為室外空氣逐時溫度，℃。

2.2.2 其他負荷的估算

通過室內熱濕源散熱散濕形成的冷負荷，包括設備，照明和人體的得熱。由于設備，照明和人員數量等輸入參數不能準確測量，導致冷負荷無法精確計算。但可以按照建筑的具體使用功能估算得到，為了保證冷負荷具有一定的富裕量要求取較大值。相關工作人員需要根據現實情況進行合理估計，將合理逐時估算值輸入程序。此外，為了與逐時冷負荷計算方法相匹配，逐時新風冷負荷需要測量計算時刻的室內外空氣焓值和新風量得到。

3 BP 神經網絡模型

3.1 BP 算法的選擇

標準BP 算法每次只是基于單個誤差Ek而言，而本文采用“累積BP 算法”，是在讀取整個訓練集里所有的訓練樣本一遍后，計算出每一個樣本數據的誤差Ek，得到每一個樣本數據的閾值和權重的變化值，在此之后會將閾值和權重的變化值累加起來更新一次，這樣不斷循環，直至訓練集的累計誤差最小化[2]，方可確定最終的閾值和權重。因為每次所有的樣本數據對于模型的改善都有貢獻，所以相比于標準BP 算法，參數更新的頻率要更快，還可以更加有效地加快收斂速度。累積BP 算法流程圖見圖3。

圖3 累積BP 算法流程圖

3.2 輸入層輸入參數的確定

室內空調負荷的影響因素主要包括外擾因素和內擾因素。外擾因素包含室外氣象參數，其中室外干球溫度和太陽輻射的影響較大。內擾因素包含室內人員、照明和設備的數量、作息和工作形式，由于室內人員情況變化較大，無法得到準確數據，因此需要對其進行模糊化處理。照明和設備相比于人員來說，影響較小也相對比較固定，可以不做考慮。綜上所述，輸入層輸入參數選取k-1 時室外干球溫度（即前1 小時）、k時室外干球溫度、含濕量、k-1 時的太陽輻射、k 時的太陽輻射和k 時人員。

3.3 神經元個數的確定

在BP 網絡中，隱含層神經元個數的選擇非常重要。Hornik et al 在1989 年證明，只需一個包含足夠多神經元的隱含層，多層前饋網絡就能以任意精度逼近任意復雜度的連續函數，然而，如何選擇最佳的隱含層神經元個數仍沒有定論，實際應用中通常采用試錯法（trial-by-error）。為了簡化模擬過程，提高試錯效率，首先通過以往種種方法確定隱含層神經元個數的最大值和最小值，然后分別以其為上下邊界從小到大開始訓練神經網絡，選出最佳神經元個數。通過對6—12 個節點分別進行試錯，發現了采用8 個節點時訓練效果最佳。

3.4 隱含層激活函數的選擇

輸入層和輸出層采用LinearLayer，隱含層采用SigmoidLayer，學習率為η∈[0,1]，訓練至直到擬合（有最大步數限制），最終輸出訓練和預測誤差，并將預測值和實際值的對比圖形化。最終的網絡結構圖如圖4所示。

圖4 神經網絡結構圖

3.5 數據預處理

3.5.1 數據集的建立

為了模擬小樣本條件下的空調負荷預測，采用某一建筑實際運行數據創建訓練所需的數據集。建筑地點位于常州，建筑高度約15 m，建筑面積約4000 m2，建筑為辦公建筑，樣本日期選取為2017 年6 月13日～9 月1 日和2018 年8 月1 日～8 月31 日，時間為每天的8:00～20:00（周六、周日除外）。之后將整個數據集導入MySQL 數據庫，并以時為間隔將其輸入神經網絡模型進行訓練，以求在最大效果上逼近在線負荷預測。采用“留出法”將數據集劃分為訓練集和測試集進行模擬，其中80%為訓練集，20%為測試集，在訓練集中訓練出模型后，用測試集來評估其測試誤差[3]。

3.5.2 歸一化處理

為了消除樣本數據量綱的影響，加速優化過程，提高訓練精度，針對樣本數據進行了歸一化處理，將原始數據處理到[0,1]區間，歸一化公式如下：

反歸一化公式：

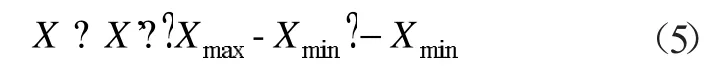
式中：X 為原始數據；X'為歸一化后的數據。

4 空調負荷的預測及誤差分析

4.1 預測結果和誤差分析

4.1.1 對內擾因素進行模糊化處理

考慮到室內人員實際數據具有不確定性，主要是缺少統計，無法準確得到其具體數據。另外數據具有一定的波動性，不穩定。決定對其進行模糊化處理，人員的取值在[0,1]之間（0 代表沒人，1 代表人滿）變化。具體數據如表1 所示。

表1 模糊化取值

為了更好地比較對內擾因素模糊化和不做考慮的誤差，分別選取10 天、20 天、30 天、40 天、50 天的訓練樣本進行預測測試，并計算了每天預測的平均相對誤差，預測誤差結果如圖5 所示。

圖5 平均相對誤差對比圖

從圖5 可以看出，相比于不考慮室內人員的情況，模糊化后的平均相對誤差普遍降低，降低幅度大體上在0.34%左右，最高降幅可達1.31%，說明將人員因素作模糊化處理后考慮進輸入參數，可以有效降低預測誤差，提高預測精度。

4.1.2 空調負荷的預測

1）在線負荷預測

衡量模型泛化能力的評估標準主要是相對誤差的大小。

相對誤差：

式中：n 為測試樣本數量；f(xi)為預測值；yi為實際值。

將預測得到的預測值和實際值進行整理，得到圖6。圖6 分別為訓練樣本為1 天，2 天和3 天的預測值和實際值的對比（負荷負值代表冷負荷）。

圖6 訓練樣本為1 天，2 天和3 天時預測值和實際值比較

如圖6 所示，訓練樣本為3 天時，起始誤差仍較大，但隨著預測的持續進行，預測精度逐步提高，14:00～20:00 的預測值已比較接近于實際值，相對誤差在1.15%～7.79%之間。通過以上分析可得，預測剛開始前幾天，大部分時刻預測值與實際值的誤差較大，總體預測情況較不穩定，這是由于建筑處于運行初期，樣本量數據較少導致的，但隨著時間的推移，訓練數據的增加，預測精度逐漸提高。

隨著預測的逐步進行，預測誤差逐漸變小，圖7 分別為訓練樣本為18 天和21 天的預測結果。

圖7 訓練樣本為18 天和21 天時的預測值和實際值

由圖7 可以看出，直到訓練至第18 天時，每個時刻的預測最大相對誤差為8.69%，最小相對誤差為0.28%，平均相對誤差為2.78%，誤差很小。訓練至21天時，每個時刻的預測最大相對誤差為10.22%，最小相對誤差為0.28%，平均相對誤差為3.08%，除12:00、13:00 兩個時刻誤差達到10%左右，其余各時刻誤差均小于3%。這兩天的預測值和實際值曲線整體契合度都較高。

為了更好地分析預測精度的變化，從訓練天數為18 天起，隨著訓練天數的逐漸增加，記錄下8:00～20:00 負荷預測的相對誤差和平均相對誤差，具體可參見表2。

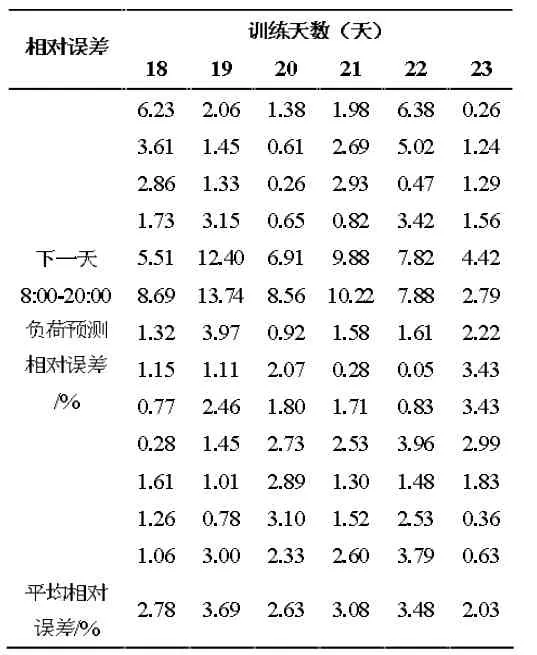
表2 負荷預測誤差表

從表2 可以看出，每天的相對誤差在10%以內的占96%，在5%以內的占85%。誤差較大的時刻主要集中在12 時和13 時，由于人員作息情況變化較大，且較不穩定，導致預測誤差相較于其他時刻明顯偏大，但是總體上每天的平均相對誤差都在4%以內。因此可以得出，從18 天以后，隨著訓練天數的增加，預測精度并沒有較大提升，負荷預測的誤差已經趨于穩定，預測值和實際值的相對誤差在一定天數內已縮減至精度范圍內，達到預期期望要求，可以選用其中預測效果相對較好且訓練時間較短的模型，最終選擇訓練天數為22天時的模型投入中期預測。

2）模型泛化性能的分析

選用2017 年6 月13 日～7 月12 日這22 天訓練所得模型，對同一年的7 月13 日～8 月3 日的空調負荷進行一次中期預測，預測結果如圖8 所示。

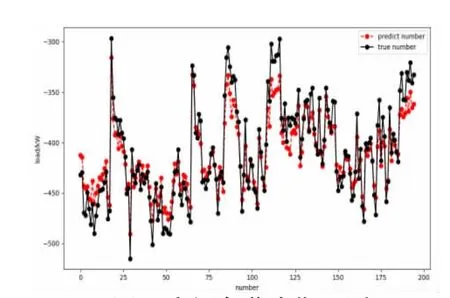
圖8 空調負荷中期預測

從圖8 可以看出，預測負荷的相對誤差在10%以內的占96%，在5%以內的占80%，最大相對誤差為12.38%，最小相對誤差為0.04%，平均相對誤差為3.42%，可以看出針對同一年之內的負荷數據的預測，泛化性能較好。

為了驗證模型長期預測的效果，使用2017 年6 月13 日～9 月1 日的負荷數據將模型訓練完畢后，采用此模型對下一年的空調負荷進行預測。由于一年的空調負荷數據過多，這里決定選取2018 年8 月1 日～8月31 日數據作為預測數據，預測結果如圖9。

圖9 空調負荷長期預測

從圖9 可以看出，預測負荷的相對誤差在15%以內的占96%，在10%以內的占81%，最大相對誤差為17.68%，最小相對誤差為0.01%，平均相對誤差為6.38%，下一年的負荷預測相比同一年的誤差有所增加，但仍在可接受范圍內，這是因為相對于一個月內的氣象參數而言，一年后的氣象參數變化情況要更為復雜，預測難度加大。

6 結論與展望

1）采用基于機理的經驗模型與神經網絡相結合的負荷預測方法，可以實現在小樣本條件下建筑空調負荷的實時在線負荷預測，為冷水機組智能控制打下基礎，便于無人值守機房的實現。

2）BP 神經網絡的學習時間冬、夏季分別需要20天左右，基本上滿足控制精度要求，模型泛化性能較好。實際工程中，隨著學習樣本的不斷增加，本文提出的模型將隨時間逐步成長，預測的精度與泛化能力將逐步提高，直至完全滿足工程要求。