基于BDS-2/BDS-3聯合處理的北斗超快速鐘差預報優化策略

馬昌忠，王潛心，胡 超，閔揚海，王澤杰

(1. 中國礦業大學自然資源部國土環境與災害監測重點實驗室，徐州 221116;2. 中國礦業大學環境與測繪學院，徐州 221116)

0 引言

目前，國際GNSS監測與評估系統(interna-tional GNSS Monitoring and Assessment System, iGMAS)發布的超快速鐘差產品中，中國北斗衛星導航系統(BeiDou Navigation Satellite System, BDS)觀測和預報部分精度分別約為0.60ns和6.00ns，遠遠不能滿足實時cm級應用需求[1]。因此，在提高全球導航衛星系統產品可用性、穩定性和可靠性的前提下，有必要進一步完善BDS超快速衛星鐘差產品質量，尤其是預報鐘差精度。

當前，針對衛星鐘差預報的研究主要集中在3個方面：1)衛星鐘差序列預處理策略[2-4]；2)預報模型精化處理[5-7]；3)環境因素對鐘差建模的影響分析[8-9]。此外，在鐘差預報算法和策略研究中，學者主要關注鐘差序列長期預報模型研究，如擴展狀態模型[10]和人工神經網絡預報[11]；多個短周期項疊加預報，如改進的迭代法以及基于恒星日濾波的單天內鐘差變化量預報等[5]。通常衛星鐘差預報模型采用趨勢項(多項式)與周期項表示[5,12]。同時，毛亞等提出了一種改進的預報策略[13]，即考慮星間相關性對模型參數估計的影響，一定程度上提升了BDS-2鐘差預報精度。

然而，BDS超快速鐘差建模中廣泛采用組合趨勢項與周期項的函數模型[2,14]，主要以全球定位系統(Global Positioning System，GPS)相關研究為參考。此外，黃觀文等提出了一種改進的BDS超快速鐘差預報策略，其中非線性項通過BP神經網絡(Back Propagation Neural Network，BPNN)進行建模處理[1]。陳金平等評估了基于星間鏈路觀測數據的BDS-3試驗星鐘差預報特性[15]。此外，研究表明BDS-3配備的星載原子鐘頻率穩定性較BDS-2提升了1個量級以上。胡超等通過引入星間相關性[16]，聯合預報了BDS-2和BDS-3超快速產品，并評估了星間相關性對超快速鐘差預報產品精度的影響[17]；基于1個月的實驗數據表明，引入星間相關性可實現BDS-2和BDS-3衛星18h預報鐘差精度分別提高30.7%～47.3%和49.9%～59.3%。因此，為進一步提高北斗超快速預報鐘差產品質量，后續研究中有必要對BDS-2和BDS-3鐘差聯合處理中的相關性系數進行深入挖掘分析與處理。

與當前廣泛使用的鐘差預報模型[1,13]相比，北斗衛星鐘差建模中，模型參數估計存在2個主要問題需要優化：1)建模過程中，通常將趨勢項與周期項分為兩部分進行獨立處理，不可避免地忽略了未知參數之間的相關性[16]；2)在建模中，只考慮顯著周期項(如BDS-2 2個周期、BDS-3 3個周期)[17]，將導致模型殘差無法建模。因此，為了獲得更準確且可靠的北斗鐘差預報模型，需要對BDS鐘差建模策略進行優化處理，如精化鐘差模型項以及模型系數等。本文將利用一步求解策略，實現北斗各衛星鐘差模型的統一估計；同時在一步模型參數估計中，對預報模型的精度、參數數目和參數類型(周期項和趨勢項個數)進行權衡；為獲得最優鐘差模型，模型參數估計中借助機器學習中稀疏建模的思想進行優化處理[18]。

本文主要針對傳統鐘差預報模型建模策略的缺點，采用BDS-2/BDS-3鐘差序列聯合處理的方法，優化北斗超快速衛星鐘差產品。首先，基于稀疏建模方法提出了一種模型選擇方法，對傳統的鐘差預報兩步策略進行改進；其次，設計了一種BDS-2/BDS-3聯合處理策略，以充分利用BDS-2與BDS-3星間相關性實現參數解算增強；然后，考慮預報模型殘差序列的時空相關性，利用半變異函數構建經驗模型，精化北斗鐘差模型參數；最后，通過大量實驗對本文的優化策略進行驗證。

1 北斗超快速鐘差預報優化策略

1.1 BDS-2/BDS-3聯合處理模型

在對北斗原始鐘差序列進行嚴格預處理的基礎上，如粗差探測與修復和降噪等[16]，可將超快速解算鐘差序列設為L，則鐘差模型可表示為[1,13,16]

(1)

式中，ti和k分別表示第ti個歷元時間和第k顆衛星；a0、a1和a2為趨勢項(多項式)系數；n為周期項總數，j為第j個周期；Aj、Bj和Tj表示周期項振幅及其相應周期大小；ε(ti)表示模型殘差項。

式(1)中，周期項通常采用快速傅立葉變換算法計算得到。因此，根據得到的周期項，相應的鐘差模型誤差方程可表示為

(2)

式中，Lk為鐘差減去周期項結果。需要注意的是，傳統鐘差序列建模策略中[16-17]，解算鐘差模型參數(趨勢項與周期項)分為2個獨立處理過程分別進行平差估計；理論上單個模型的所有參數需經統一解算得到。同時，由于星載原子鐘的特性存在差異，所有鐘差模型參數的個數和類型不可能表示為統一形式；因此，為獲得更精確的鐘差模型，有必要細化北斗鐘差模型參數。

首先，一步估計式(2)中所有模型參數。為提高計算效率，同時解算所有衛星多項式參數，假設有b顆衛星、s個歷元，式(1)矩陣形式為

(3)

(4)

式(4)中，權矩陣P(t1)可表示為

(5)

rkb=

(6)

在鐘差模型參數估計中，有必要對權陣進行調整，以提高預報模型的精度，本文在權陣中引入時間變量，即

(7)

式中，Δt表示相鄰歷元的時間間隔。式(2)～式(7)，即為基于BDS-2/BDS-3星間相關性的北斗鐘差預報模型一步建模策略。

1.2 基于稀疏建模的鐘差模型估計

在1.1節的基礎上，鐘差模型參數估計考慮了衛星間相關性，間接地優化了模型參數求解過程。然而，參數估計中仍存在2個關鍵問題會導致待估參數無法獲得最優解：1)由于建模中觀測值(鐘差序列)有限和模型過度擬合等因素影響，模型參數的穩定性和精度不可避免地受到限制；2)不同類型星載原子鐘呈現出不同的特性(鐘差模型)[19]，無法基于統一的模型進行描述(相同的待估參數)。為提高鐘差建模精度與穩定性，有必要進一步優化北斗衛星鐘差建模策略。

本節利用機器學習中稀疏建模的思想進行鐘差模型精確構建。理論上，引入所有的自變量進行建模處理可有效提高建模精度，但同時也增加了模型復雜性并導致過度擬合。在實際應用中，為了提高模型的可靠性與預報精度，必須考慮模型自變量的合理選取，即模型選擇(或變量選擇)[20-21]。通常，模型選擇只能在有限的備選模型范圍內進行，而稀疏建模可以有效地選擇建模數據與自變量(模型項)，從而實現模型預報精度和計算效率的提升。為對北斗鐘差序列進行稀疏建模處理，本文采用Tibshirani提出的最小絕對值收斂和選擇算子(Least absolute shrinkage and selection operator，Lasso)算法[22]。在Lasso算法中，通過最小化多變量線性回歸模型的損失函數，對回歸系數絕對值施加約束，實現了參數估計和模型選擇同步進行。根據Lasso算法原理，可實現對部分變量進行壓縮和消除；Lasso算法的具體實現是通過L1范數的最小二乘法，即

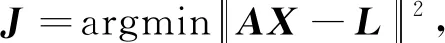
(8)

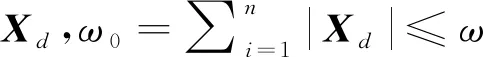
(9)

式中，λ為正則化系數。等式右邊相當于模型殘差平方和與正則化函數的組合；區別于Tikhonov正則化的L2范數，L1正則化范數通過自動模型選擇達到稀疏性的同時，不失函數模型的凸性(產生少量特征)。為求解式(9)，可通過迭代加權最小二乘法求解Lasso問題的數值解[23]，即式(9)可表示為

(10)

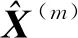
(11)

式中，U(m)是權陣(對角陣)，其元素根據第m-1次迭代解確定。因此

(12)

通過矩陣求逆公式，式(12)的解為

(13)

1.3 基于半變異函數的模型殘差處理

通過上述基于稀疏建模思想的一步求解鐘差模型參數，可較好地實現北斗鐘差預報模型構建。但是受模型殘差以及隨機噪聲影響，建模過程中需對模型殘差序列進行深入分析。前期研究中，針對預報模型殘差序列提出了幾種改進的處理策略[1,13]；此外，學者組合了偏最小二乘法(Partial Least Square，PLS)和BPNN算法，并將其應用于超快速鐘差預報中[14,17]；但缺少衛星鐘差精度的相關信息(方差-協方差陣)，殘差序列建模及其預報難以達到預期精度[17]。本文從鐘差序列特點的角度考慮，即所有衛星建模殘差序列不可避免地呈現時空相關性；因此，為充分挖掘BDS-2與BDS-3鐘差序列各衛星潛在的時空特性，本節提出了利用半變異函數進行殘差序列優化處理。有關半變異函數的更多細節已在相關研究中進行了詳細討論與總結[17,24-25]。

在實際建模處理中，通常使用改進的殘差半變異函數模型[19,24]

(14)

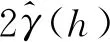
2γ(ti,tl)=2(C(0)-C(ti-tl))

(15)

式中，C表示參數協變差運算。C(tl-ti)可以通過式(16)計算得到

C(ti-tl)=Cov(ε(ti),ε(tl))

(16)

其中，Cov表示協方差運算；模型殘差的時間相關性將由半變異函數進行數值量化。

在得到每顆衛星量化的殘差序列時間相關性之后，可擬合出經驗半變異函數模型，如球形和指數型等。基于得到的經驗半變異函數模型(如式(17)與式(18))，當h→∞時，2γ(h)→2C(0)；由式(15)可知，協變差C(h)可由經驗函數模型確定。因此，在式(16)的基礎上可進一步構造參數估計的權陣，并將其代入式(3)中，從而實現模型系數估計的精化處理。

綜上，本文從星間相關性、稀疏建模以及半變異函數等3個方面對北斗超快速預報鐘差模型進行了精化處理。首先，基于稀疏建模對鐘差模型參數進行一步估計，實現了模型的自動選擇，并改進了傳統鐘差分步建模策略；其次，考慮BDS-3星載原子鐘具有更強性能，通過提取星間相關性實現了模型參數的解算增強；最后，針對模型殘差序列，利用半變異函數對參數估計隨機模型進行了精化處理。

2 BDS-2/BDS-3衛星鐘差預報實驗分析

本節將對改進的BDS-2/BDS-3衛星超快速鐘差聯合預報策略進行實驗分析。實驗前，首先基于連續1個月(2019年第41～70天)的BDS-2和BDS-3觀測數據進行超快速聯合定軌實驗，得到了解算的超快速衛星鐘差產品。鐘差預報實驗中，根據本文提出的改進策略，將實驗分為3組，分別從星間相關性、稀疏建模和半變異函數模型的角度對鐘差預報模型進行驗證分析。考慮到北斗地球靜止軌道(Geostationary Earth Orbits，GEO)衛星鐘差精度較低的特點，在實驗中剔除了相應部分。

第1組實驗中包括4個對比方案，驗證了基于稀疏建模的鐘差序列一步建模策略：

方案1：基于趨勢項和周期項，建立鐘差預報模型，該方案中，趨勢項系數通過擬合鐘差序列得到，而周期項則通過殘差的快速傅里葉變換確定；

方案2：與方案1類似，其中BDS-2衛星周期項參考黃觀文等[1]以及毛亞等[13]的研究結論，BDS-3則利用3個主要周期項建立鐘差預報模型；

方案3：與方案1和方案2相比，將快速傅里葉變換獲得的所有周期項加入鐘差序列建模中；

方案4：在方案3的基礎上，采用Lasso算法對模型參數進行一步估計，以驗證稀疏建模的有效性。

根據上述四種方案分別進行了1天弧長的BDS鐘差預報實驗，并以武漢大學iGMAS分析中心發布的BDS快速鐘差為參考進行精度分析。各方案中BDS-2與BDS-3衛星的鐘差建模殘差以及相應預報精度如圖1和圖2所示。

通過上述4套對比實驗方案可知：1)BDS-3衛星鐘差建模殘差明顯小于BDS-2衛星，間接說明了BDS-3星載原子鐘性能優于BDS-2；2)方案1與方案2的擬合殘差近似相等，而方案3中利用所有周期項建模得到的模型殘差最小；3)基于圖2中鐘差預報精度的統計結果，對BDS-2而言，方案3較傳統方法(方案1與方案2)預報精度有所提高，且方案4(一步建模)略優于方案3(除C13外)；對于BDS-3衛星，方案3一步估計所得到的預報精度有所降低，但在稀疏建模之后(方案4)，在方案1與方案2的基礎上，一定程度實現了預報精度的提高。

圖1 年積日41天(2019)不同北斗衛星鐘差擬合殘差Fig.1 Fitting residuals of BDS clock offsets for different satellites on DOY 41

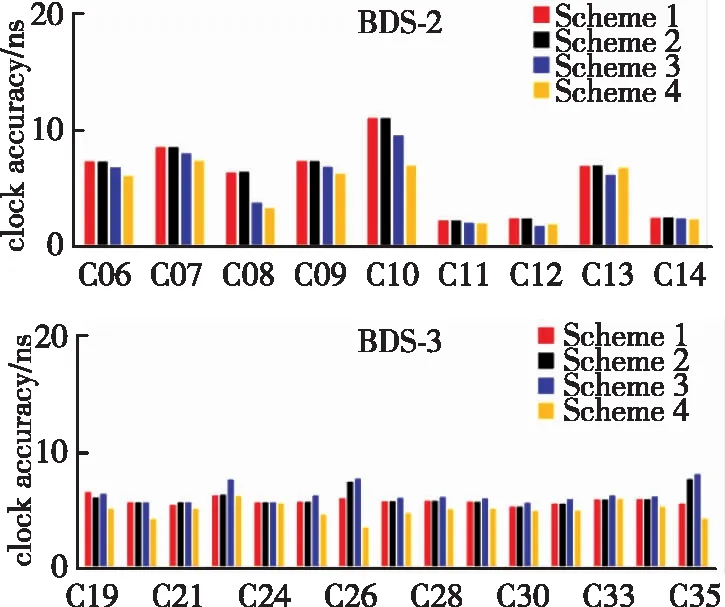
圖2 四種方案連續30天北斗鐘差預報精度(18h)平均值Fig.2 Average daily RMS values of BDS predicted clock offsets for different satellites in 30-day experiments with four schemes (18 hours)

第2組實驗包括2個對比方案，驗證了引入星間相關性求解模型參數的可行性：

方案5：類似方案1，但在模型參數求解中加入了星間相關性系數，該方案具體實驗細節可參考作者前期研究成果[16-17]；

方案6：同樣地，在方案4的基礎上，將獲取的星間相關性系數加入衛星鐘差模型參數估計中。

圖3所示為連續10天C14與C24衛星預報鐘差的精度；表1則給出了1個月鐘差精度平均值(18h)及其精度提升率。實驗結果表明，星間相關性可顯著改善北斗衛星預報鐘差精度；且與傳統建模方法(方案1)相比，BDS-2與BDS-3衛星鐘差預報精度分別提升了32.9%和16.9%；而方案4考慮了星間相關性后，BDS-2與BDS-3衛星鐘差18h預報精度分別提升了27.2%與28.6%。

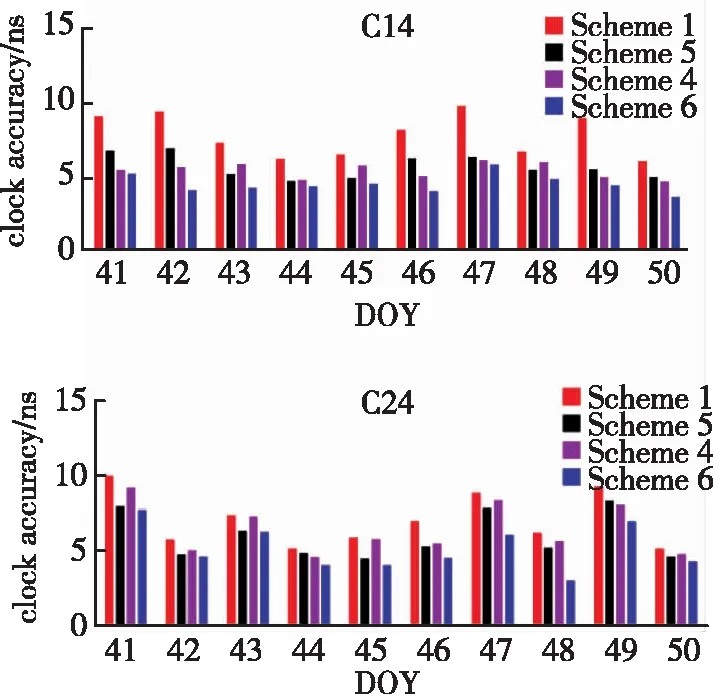
圖3 不同方案連續10天鐘差預報精度Fig.3 Prediction accuracy of clock offsets in 10 consecutive days for different schemes

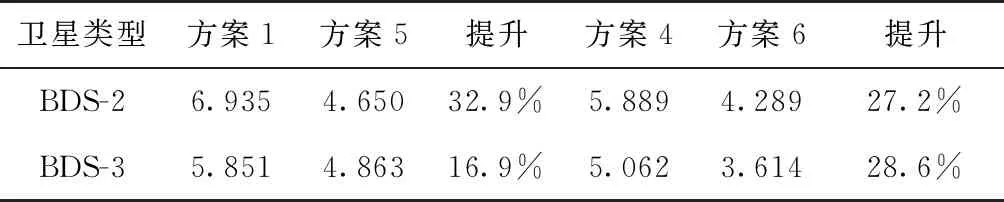
表1 不同方案北斗衛星鐘差預報精度(ns)及其提升率(18h)

通過上述引入星間相關性與稀疏建模處理后，模型殘差中仍包含了鐘差序列的有效成分，其一定程度上降低了北斗鐘差預報的精度。第3組實驗主要分析了本文提出的超快速鐘差預報策略的正確性，并驗證了利用半變異函數精化模型參數估計的隨機模型的可行性。在鐘差預報實驗前，首先基于方案4中的模型殘差序列進行時空相關性估計，結果如圖4所示，其中虛線表示基于1個月殘差序列計算的實驗半變異函數值；其次，構建了一個經驗模型，即半變異函數模型，實驗中選擇球面模型進行殘差半變異函數模型構建，即如式(17)與(18)所示

γ(h)BDS-2=

(17)

γ(h)BDS-3=

(18)

圖4 BDS-2和BDS-3方案4鐘差殘差序列半變異函數Fig.4 Variogram from the satellite clock offsets residuals of scheme 4 for BDS-2 and BDS-3 satellites

方案7：基于BDS-2與BDS-3聯合超快速鐘差序列，考慮星間相關性，通過方案1進行鐘差預報；

方案8：基于BDS-2與BDS-3聯合超快速鐘差序列，考慮星間相關性，通過方案2進行鐘差預報；

方案9：基于BDS-2與BDS-3聯合超快速鐘差產品，通過方案6進行鐘差預報，每個預報弧段長度為18h，并利用BPNN算法對模型殘差進行處理與預報，最后將兩部分預報鐘差序列合并；

方案10：類似于方案9，針對模型殘差部分采用灰色模型進行預報處理；

方案11：基于方案6，采用PLS+BPNN策略對模型殘差進行建模與預報處理[24]；

方案12：基于方案6，采用經驗半變異函數模型計算的模型殘差協方差陣對式(4)中的權陣非對角線元素進行更新處理，同時采用PLS+BPNN策略對模型殘差進行建模與預報處理。

為對本文提出的改進的鐘差預報模型進行全面分析，將實驗中12個預報方案結果與WHU的快速鐘差產品進行對比。為討論不同方案的鐘差預報精度，圖5中選取了6套方案中C14與C24衛星對比分析建模殘差的差異，通過模型殘差可明顯發現方案11的建模效果最優。

圖5 基于2019年第41天的C14和C24不同方案模型殘差Fig.5 Model residuals of different schemes based on DOY 41, 2019 for C14 and C24 satellites

同時，為具體說明方案7～12中不同實驗的鐘差預報精度，表2給出了不同方案下鐘差預報精度平均值。由于超快速鐘差產品以3h時延和6h間隔進行更新發布[16]，因此，鐘差預報結果中僅分析了1天內18h的鐘差預報精度。

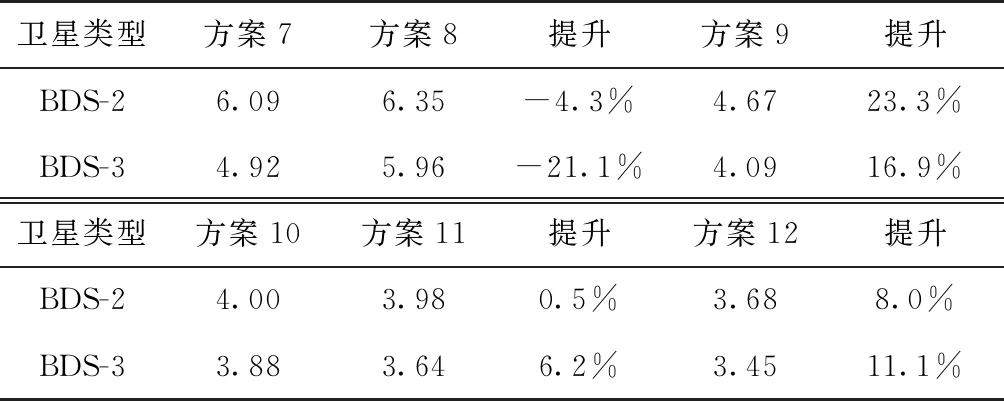
表2 基于傳統方法、星間相關性和Lasso算法的18h超快鐘差預報精度(ns)及不同方案提升率

基于圖5與表2中各方案的統計結果，可以得出：1)與方案2相比，考慮BDS-2/BDS-3衛星鐘差相關性對模型殘差的影響不明顯；2)基于廣泛使用的周期項選取方法進行鐘差建模，將導致BDS-2與BDS-3預報鐘差精度分別下降4.3%和21.1%；3)通過灰色模型對模型殘差進行處理，BDS-2與BDS-3鐘差預報精度分別提高了23.3%與16.9%。需要說明的是，方案8是在傳統方法的基礎上進行建模優化處理，需對其模型殘差進行補償。因此，實驗中設置了基于BPNN和PLS+BPNN算法的鐘差殘差序列預報方案。實驗結果表明，PLS+BPNN策略可實現模型殘差較傳統BPNN算法建模降低0.5%和6.2%。同時，由于模型殘差序列中存在時空相關性，在系數估計中引入半變異函數對權陣進行精化處理，方案12較方案11可進一步實現BDS-2與BDS-3預報鐘差精度分別提升8.0%與11.1%。

3 結論

本文基于前期研究，對BDS-2/BDS-3聯合超快速鐘差預報策略進行了優化處理，并通過3組共12套實驗方案進行驗證，可以得出：

1)由于傳統鐘差模型的兩步求解過程存在精度損失現象，提出了一步估計模型參數(趨勢項和周期項)的策略；并引入機器學習中的稀疏建模方法對鐘差模型參數進行自動篩選；基于鐘差預報結果可知，一步建模策略可略微提升鐘差預報精度。

2)考慮到BDS衛星(BDS-2與BDS-3)的差異及星載原子鐘的特點，文中將星間相關性作為一種間接方法增強模型系數求解；結果表明，基于一步建模策略，通過引入BDS-2與BDS-3星間相關性，可實現BDS-2與BDS-3衛星18h鐘差預報精度分別提升27.2%與28.6%；

3)在建立鐘差預報模型時，基于鐘差殘差序列，構造經驗半變異函數模型提取殘差序列中的時間相關性，并將其納入模型系數估計的權陣更新中。與已有文獻提出的方法相比[6,24]，該策略可進一步實現BDS-2與BDS-3衛星鐘差預報精度分別提升8.0%和11.1%。

綜上，本文提出的BDS-2/BDS-3聯合超快速衛星鐘差預報策略可改善分析中心北斗鐘差產品的精度。但是，本文改進后的策略只基于1個月的實驗進行測試分析，因此，針對BDS-2/BDS-3聯合超快速衛星鐘差預報策略的可用性和準確性還需進一步研究和分析。