基于STDP規則的脈沖神經網絡研究
莊祖江,房 玉,雷建超,劉棟博,王海濱
(西華大學 電氣與電子信息學院,成都 610039)
0 概述
脈沖神經網絡(Spiking Neural Network,SNN)[1]被稱為第三代神經網絡[2],是目前最具有仿生性的人工神經網絡。腦科學的研究結果表明,在生物系統中,信息是以突觸直接的動作電位來進行處理和傳遞的。受這一研究的啟發,脈沖神經網絡將信息編碼成脈沖序列進行處理,其結構更接近于生物神經元,而且網絡的計算能力強于傳統人工神經網絡[3]。由于其優秀的性能,引發了諸多學者的關注,如英國帝國理工大學的GOODMAN研發了脈沖神經網絡的仿真平臺Brian[4-5],奧地利的MAASS對脈沖神經元模型、網絡拓撲結構和相關應用進行了研究[6-7],日本東京大學KUBOTA等人將SNN應用到助力機器人以及行走機器人上[8],瑞士聯邦學院GERSTNER等人對脈沖神經元模型和脈沖時間獨立可塑性學習規則等理論進行了研究[9]。國內也有學者對此進行了研究,如文獻[10]對基于脈沖時間網絡的圖像分割應用進行了研究,而且提出了累加和累積合成核機制進行網絡的訓練[11],文獻[12]將自組織網絡與STDP相結合對算法進行研究,也有學者提出了基于脈沖神經網絡的片上網絡路由器動態優先級仲裁策略[13]。
研究人員對脈沖神經元模型進行深入研究,目前學界比較公認的學習算法有脈沖時間依賴可塑性(Spike-Timing-Dependent-Plasticity,STDP)[14]、Tempotron[15]、ReSuMe(Remote Supervised Method)[16]和SpikeProp[17]等,STDP算法由Hebb規則[18]延伸而得到,是目前比較流行的無監督算法[19],能夠較好地解釋神經網絡的依賴性。
本文研究基于無監督的脈沖神經網絡,采用STDP學習算法進行基于脈沖數目的無監督訓練,通過改進傳統的分類方法,提出一種投票競爭機制提高網絡的分類準確率,并在MNIST數據集上進行實驗驗證。
1 脈沖神經網絡結構
1.1 脈沖神經元模型
脈沖神經元是構成脈沖神經網絡的基本單元,其狀態主要由膜電勢以及閾值所決定,膜電勢主要由來自上一層所有連接的突觸后電勢決定,其中EPSP(Excitatory Post-Synaptic Potential)能夠提高神經元的膜電勢,IPSP(Inhibitory Post-Synaptic Potential)能夠降低神經元的模電勢[20]。本文網絡的脈沖神經元模型采用LIF模型進行研究[21],其模型描述如下:
(1)
其中,v(t)表示在t時刻神經元的模電壓,Vr表示靜息膜電位,Ve和ge表示興奮性突觸的平衡電壓和電導,Vi和gi表示抑制性突觸的平衡電壓和電導,τm表示神經元的膜電位時間常數由τ=RC所決定,R表示膜電阻,C表示膜電容,τge和τgi分別表示激勵性神經元和抑制性神經元的膜電位時間常數。
當突觸后神經元接收到突觸前神經元傳輸的電流I時,膜電勢會升高,當其逐漸升高超過閾值時,就會釋放脈沖,隨后電勢會低于之前的靜息電位,在復位后的幾毫秒內,神經元處于不應期,不能再次出現脈沖。其電位變化方式如圖1所示。
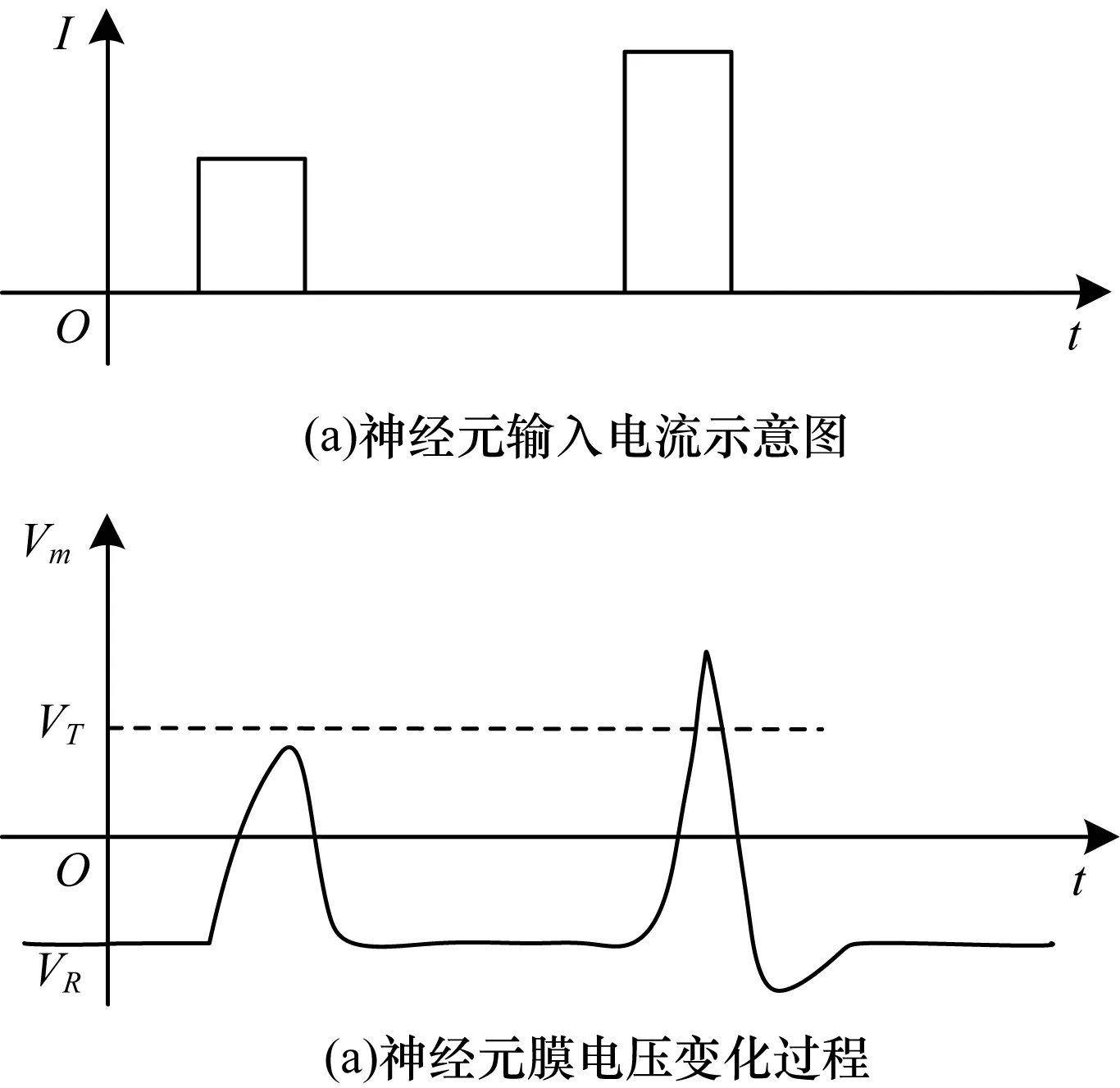
圖1 神經元輸入電流膜電壓變化過程
上述過程被稱為神經元的動作電位,也就是神經元產生了一個脈沖。從圖1可以看出,第1次輸入電流較小時,膜電壓Vm升高,但是沒有超過閾值VT,因此又恢復到靜息電壓VR,第2次輸入電流時,Vm超過了VT,因此產生了一次完整的動作電位,向突觸后神經元釋放了脈沖。
1.2 STDP算法
脈沖時間依賴可塑性(STDP)是調節大腦中神經元之間的連接強度的生物學過程,該過程根據特定神經元輸入脈沖的相對時序調整連接強度[22]。其學習機制可以表達為:
(2)
其中,tpost表示突觸后神經元產生脈沖的時間,tpre表示突觸前神經元產生脈沖的時間,表明了突觸權重的變化由所有突觸前神經元的脈沖發放時間和突觸后的脈沖發放時間所影響,常規的STDP時間函數如下:
(3)
其中,Δt表示突觸后神經元產生脈沖的時間tpost和突觸前神經元產生脈沖時間tpre之差,A+和A-代表權重調整的范圍,τ+和τ-表示不同神經元模型的常量。由式(3)還可以看出,當突觸后神經元在突觸前神經元之前產生脈沖時,則減少兩者之間的權重,反之如果突觸后神經元在突觸前神經元之后產生脈沖,則增加兩者之間的權重。
1.3 網絡結構
脈沖神經網絡結構如圖2所示,脈沖神經元網絡結構的主體是輸入層和STDP層,轉換層的作用是簡單地進行圖像樣本的處理,抑制層是抑制STDP層不活躍的神經元釋放脈沖,而分類層是將STDP層所產生的信號根據算法進行分類。
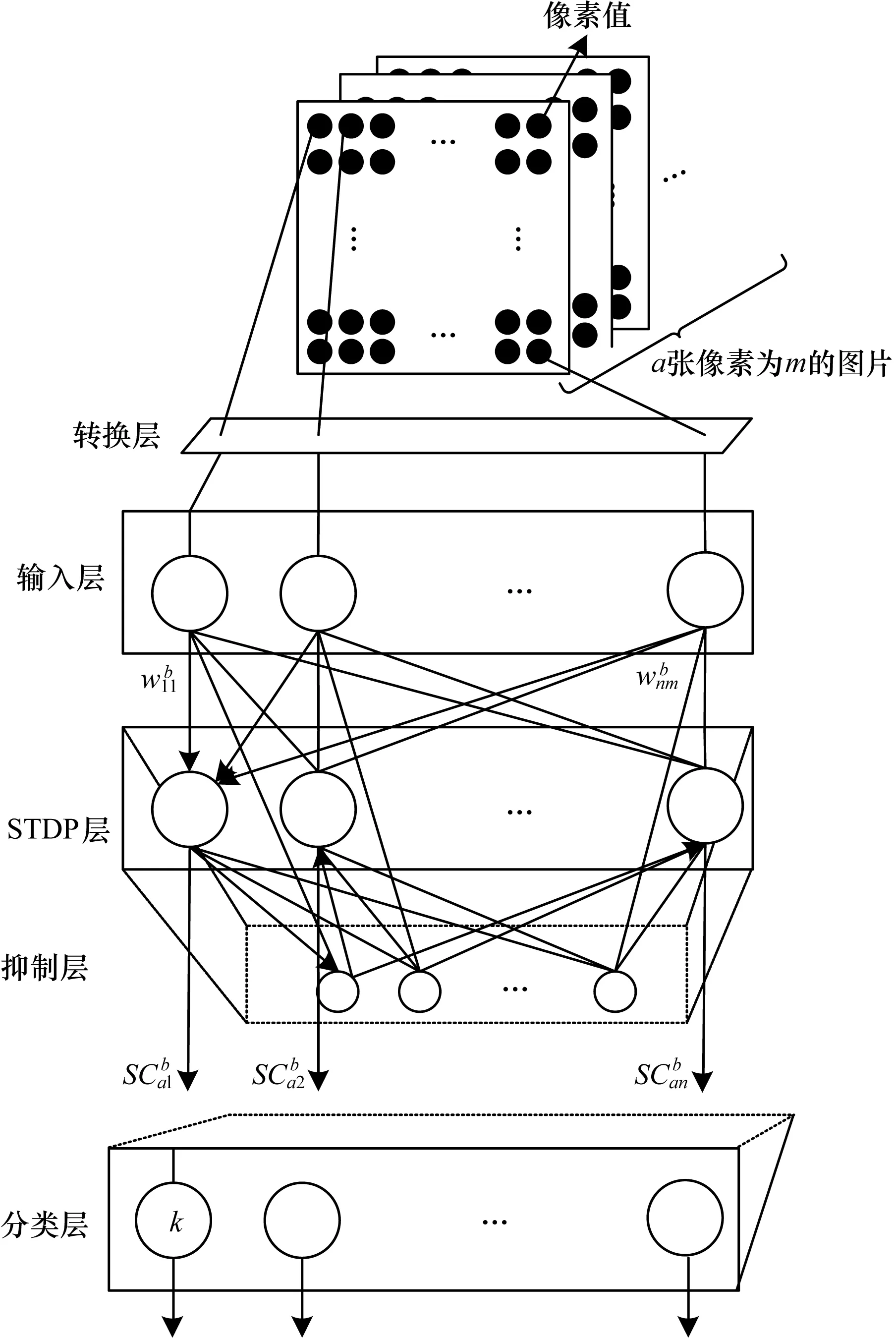
圖2 脈沖神經網絡結構
圖像的像素先經過轉換層轉換為脈沖頻率,脈沖頻率與圖像的像素強度成正比,比例系數為β,將對應的頻率傳輸到輸入層。由于本文將采用基于STDP學習規則,Poisson序列的編碼可以更好地提高效率[23],因此輸入層采用m個Poisson神經元構成,作用是可以將脈沖頻率轉換為Poisson序列,其神經元激發概率公式為:
(4)
其中,PT[n]表示神經元產生脈沖的概率,n表示神經元數目,r表示樣本數據,即脈沖頻率,T表示一次訓練的周期。
輸入層的神經元與STDP層以及抑制層的神經元是一一連接的,區別在于,與STDP層連接的權重wmn是由STDP學習規則進行更新的,而與抑制層的神經元的連接是固定權重,這樣方便調整抑制層的抑制程度。
由于網絡結構采用的是無監督學習規則進行學習,因此引入抑制層進行競爭,這樣可以使獲勝神經元的權重增加,而其他神經元的權重減少,有效降低了訓練過程中的噪聲,得到了更好的訓練效果。
對于網絡的STDP層以及抑制層在訓練過程中都是無監督的,在訓練結束之后會收斂,這樣的網絡并沒有表現出任何特定的功能。在這里需要添加分類層去識別STDP層在訓練過程中所發送的信息,以達到分類的目的。
2 投票競爭機制
分類層的算法對于網絡最后的表現至關重要,具有生物意義的常規方法是將STDP層在訓練時產生的脈沖表現轉換為每一個神經元表現的分類,然后通過加權的方式進行分類。這類方式準確率相對較低,本文針對此方法進行了改進,提出一種符合生物競爭的策略,增加了投票競爭機制,增加了分類的準確率。由于會使用到數據的標簽,但是數據不會再向前傳輸也不會改變訓練好的權重,因此本文算法為半監督類型的算法。
對于一個訓練樣本數量為a的m個像素的k分類問題,輸入神經元個數為m個,STDP神經元數目為n個,抑制層神經元數目為l個,且定義:
a1+a2+…+ak=a
(5)

1)當ak類輸入時,求出所有神經元的輸出脈沖之和并進行標準處理,可以得到平均輸入一次樣本時神經元的脈沖產生情況:
(6)
2)對于得到的k個行向量rk,定義rkn表示輸入類別為ak時,第n個神經元產生的脈沖數,可以拼接成如下的矩陣:
(7)
3)對Rkn的每一列取其最大值的行標號,作為此神經元的表現類別,可以得到:
assb=(s1,s2,…,sn)
(8)
其中,s1,s2,…,sn表示對應神經元表現的類別。
4)將前面得到的ass通過投票競爭機制進行篩選,即:
ass*=f(ass1,ass2,…,assb)
(9)
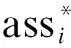
for i =1 to n :
for j =1 to b :
If 在b次訓練中無法重復值:
end
end
投票競爭策略如圖3所示,s1由s1,s2,…,sn投票得出,為其中出現次數最多的類別,即對于最后的神經元表現,由前面b次訓練過程中得到的神經元表示進行投票,若神經元表示類別為k的次數最多則最終結果定為k,這樣得到的表現類別優于之前得到的單一表現,可以使得此算法收斂到一個更優的值。

圖3 投票競爭策略示意圖
3 實驗結果與分析
為驗證投票競爭機制的可靠性與有效性,本文以配有16 GB內存、處理器為Intel?CoreTMi7-4720HQ,并裝有Ubuntu16.0的操作系統的筆記本電腦為測試平臺,以python3.6為編程環境,使用BRIAN2作為仿真庫使用,在MNIST數據集上進行了驗證實驗。
為表明網絡結構的生物意義的合理性,本文模擬時采用的參數均為在生物學的合理范圍之內,包括膜的時間常數、突觸模型和訓練周期等[24],除了提高激勵性神經元的時間常數到100 ms,相較與生物神經元中的時間常數10 ms~20 ms,該網絡結構可以降低噪聲的影響。例如,如果輸入脈沖在126 Hz的最大速率下持續輸入20 ms,則神經元平均產生2.52個脈沖,這意味著單個噪聲尖峰會產生很大的影響,而增加到100 ms時,神經元平均可以積累12.6個脈沖,從而減少了噪聲的影響。
在算法設計上,為保證算法的有效性不會因為隨機的參數起點不一致而導致誤差,本文在同等網絡結構下均采用相同初始條件。
MNIST手寫數字數據庫,其訓練集包含了60 000張28×28的圖片,測試集包含了10 000張28×28的圖片,因此網絡的輸入層神經元個數為28×28=784個。對于STDP層和抑制層的神經元數目在實驗中發現兩者相等時表現最佳,因此本次實驗過程中均選取一致的數目,測試的準確率為測試集的準確率。
為研究不同投票次數對準確率的影響,設置了一組在STDP層神經元數量不變時,訓練次數為2次~9次的驗證性實驗,實驗結果如圖4所示。
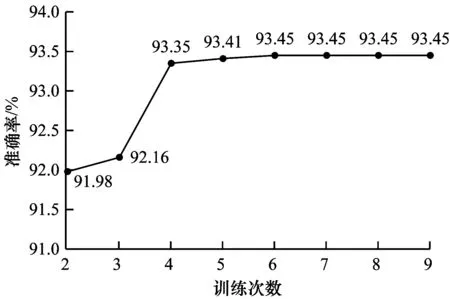
圖4 訓練次數對準確率的影響
從圖4可以看出,隨著訓練次數的增加,準確率的提升逐漸收斂,當訓練次數為4次時,測試集準確率已經穩定,這是由于本文算法的機制所表現,因為逐步增加投票的樣本,并不會很大程度地改變主神經元組的表現,因此可以看出,本文方法是有效的。為進一步驗證算法的有效性,本文設計了4次不同神經元數量下的對比實驗,實驗結果如圖5所示。其中,在不同神經元數量中,最右的深色為本文采用的投票競爭機制算法,其余為進行投票的樣本。
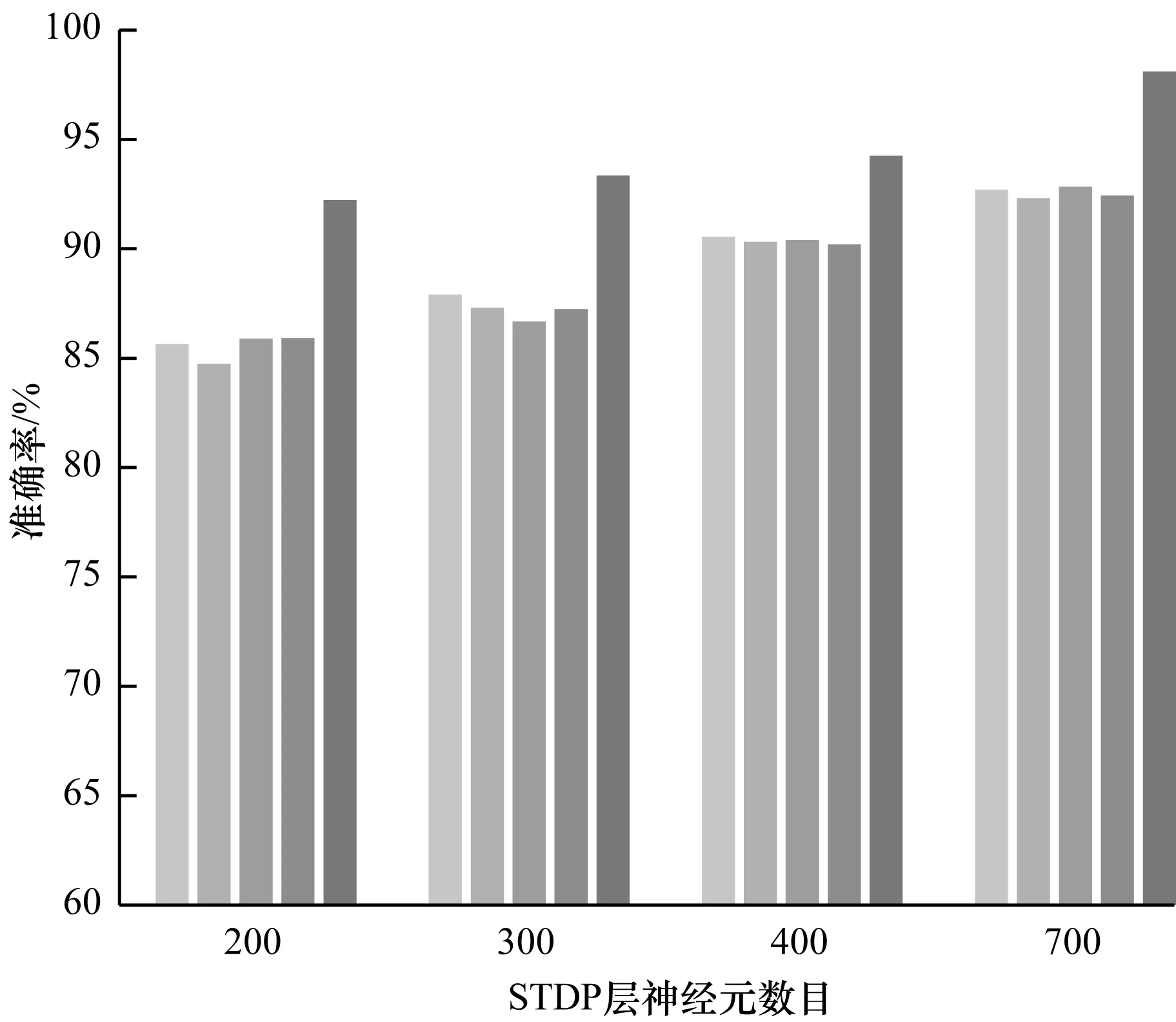
圖5 不同神經元數目下MNIST的準確率對比
當神經元數目為200時,未采用投票競爭機制的平均準確率只有85.55%,當采用本文方法后提升至92.23%,提高了6.68%,在其他神經元規模下,本文方法準確率均有較大提升,說明了本文方法可以提高脈沖神經網絡結構的分類表現。
為進一步研究準確率的提升,在神經元數目為400時,2種不同方法STDP測試集表現的混淆矩陣如圖6所示。
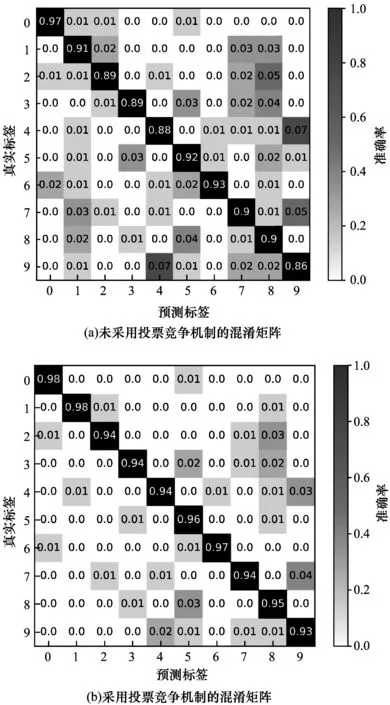
圖6 兩種方法標準化的混淆矩陣
從圖6可以看出,圖6(b)相對于圖6(a)提高了數字4和9的誤分類情況,數字9的識別率提高了6.0%,整體準確率提升了3.69%,說明本文方法是有效的。
同時為了更加嚴謹地分析算法性能,對于算法的運行時間進行了實驗分析。本文算法增加時間復雜度主要有2個因素:1)增加了競爭投票算法,由算法描述可知,此算法的時間復雜度為O(nb),受到神經元個數以及訓練次數的影響,將神經元的類別ass采用矩陣形式的存儲方式,運算效率高,時間復雜度可以降低為O(b),因此該因素對于整體的影響不大;2)增加了訓練次數,不可避免地會增加脈沖訓練時間。脈沖訓練時間影響主要來源為:不同數目的神經元網絡構建時間不同,即網絡結構創建耗時;超過指定的脈沖響應周期(接受脈沖時間和不應期時間)的額外仿真耗時。實驗結果如圖7所示。
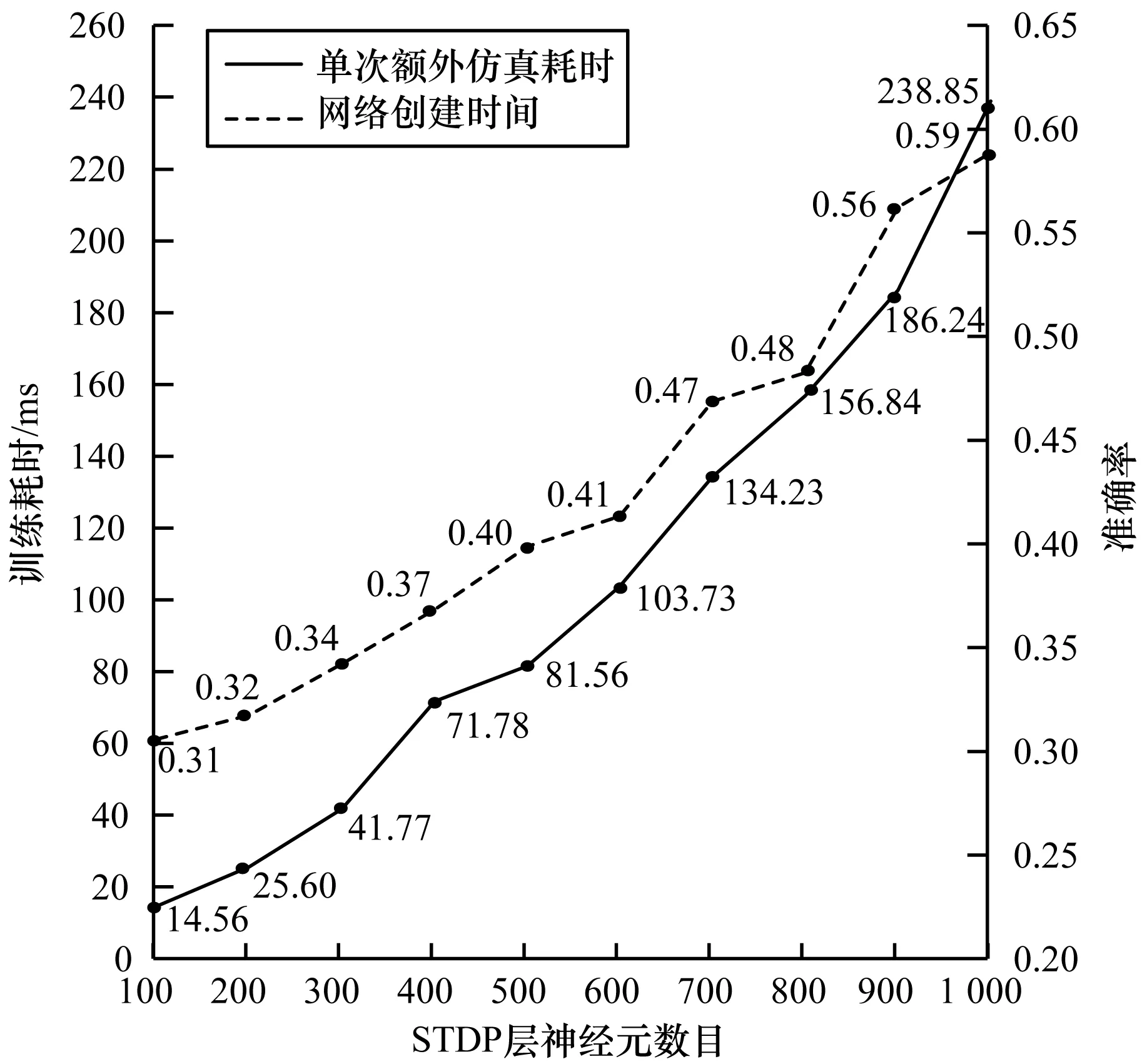
圖7 脈沖時間網絡創建與訓練耗時分析
由實驗結果可以看出,網絡創建時間和單次額外仿真耗時(取訓練同樣的前1 000個樣本時間然后取均值)均隨神經元數目的增加而增加,此處的神經元數目均指STDP層神經元數目,其余神經元數目保持不變。觀察圖中的網絡創建時間對于算法的效率影響不是很大,主要的時間影響因素來自單次額外仿真時間。對于本文算法來說,訓練4次左右提升效果最為明顯,以200個神經元訓練時長為例,單次訓練需要25.60 ms,采用本文算法則相當于需要102.4 ms,單次仿真時間比700個神經元所需的單次額外仿真時間要低1.33 ms,而兩者準確率僅相差0.34%。這說明本文算法在不增加訓練時間的情況下,可以取得與更加復雜的網絡結構一樣的訓練結果,表明本文算法對于性能有限的機器有很大的幫助。將本文算法與其他脈沖神經網絡算法在MNIST測試集上的分類效果進行對比,如表1所示。

表1 脈沖神經網絡在MNIST測試集上的比較
從表1對比結果可以看出,本文算法網絡結構的效果更好。
4 結束語
本文提出一種投票競爭機制,該機制優化了基于無監督學習的脈沖神經網絡機構在圖像分類問題的表現。采用脈沖神經網絡模型,并基于STDP學習規則進行數據訓練,對輸出的脈沖表現采用投票競爭的學習機制,提高了神經元的表現。實驗結果表明,在網絡結構一致的情況下,本文方法在訓練次數較少時即可以達到收斂,與傳統的網絡結構相比準確率提升明顯。下一步將考慮輸入網絡數據來增加預處理的過程,以降低網絡的復雜度。

