拱橋短吊桿抗彎剛度的研究分析

古 銳，陳惟珍，徐 俊

(1.四川省公路規劃勘察設計研究院有限公司,四川成都 610041；2.同濟大學橋梁工程系,上海 200092)

宜賓南門大橋、新疆孔雀河大橋等中承式拱橋相繼發生了橋面坍塌，該類事故具有很多相似之處，都是由于短吊桿驟斷，導致橋面局部坍塌。慘痛的代價證明，大跨中承式拱橋的吊桿，尤其是短吊桿，受力非常復雜，既是橋梁的關鍵受力構件，也是橋梁的薄弱部位，常常成為控制此類橋梁壽命的關鍵構件，因此有必要對短吊桿的受力行為進行深入的研究[1]。

在拱橋分析計算中，常將吊桿作為軸向受拉桿件，一般不考慮其抗彎剛度，只考慮吊桿受拉的情況。但在實際橋梁運營中，吊桿的抗彎剛度是存在的，尤其是短吊桿，以現在廣泛采用的成品吊桿拉索為例，由于鋼絲有塑包帶纏包扎緊，再外擠高密度聚乙烯護套，外徑達 5～20 cm，鋼絲之間還存在著互相摩擦、咬合等現象，所以吊桿拉索具有一定的抗彎剛度。

下文中擬以一座既有中承式鋼管混凝土拱橋為背景，對短吊桿的抗彎剛度進行研究分析。

1 工程概況

某中承式大跨徑鋼管混凝土拱橋，主跨計算跨徑為150 m，計算矢跨比為1/4.5。全橋橫向設置2道拱肋，拱肋截面由4根φ660 mm鋼管構成。橋面系采用吊橫梁、縱置小T梁，吊桿縱向間距5 m，行車道梁為標準跨徑5 m和7.5 m的鋼筋混凝土T梁，橋面寬度為24.5 m。墩臺基礎均為明挖基礎，引橋橋墩為柱式墩。全橋共有 46根吊桿，采用鐓頭錨錨固于拱肋上緣和橫梁下緣；每根吊桿采用138根φS5平行鋼絲束，采用外套φ110 mm×5 mm薄壁鋼管并內填C10混凝土砂漿防護，橋梁立面布置及吊桿截面如圖1所示。

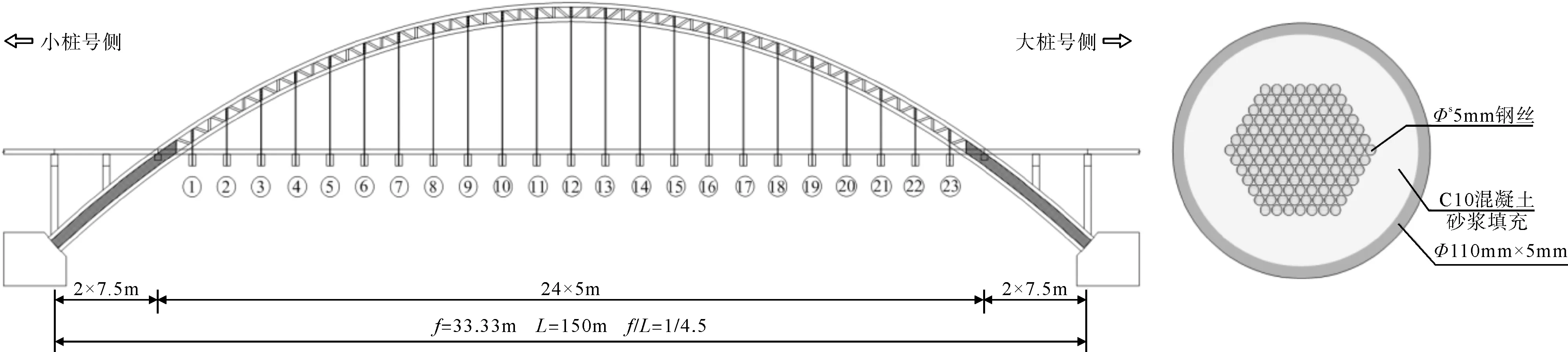
圖1 橋型布置圖及吊桿截面構造

采用有限元軟件ANSYS建立橋梁的空間模型，如圖2所示，全橋共計5 397個節點，5 868個單元。模型中吊桿采用空間單向受拉三維桿單元 Link10單元模擬，其余構件如拱肋、拱肋之間的腹桿、吊桿橫梁、立柱橫梁、立柱、橫撐和橋面系主梁等均采用Beam188單元模擬。

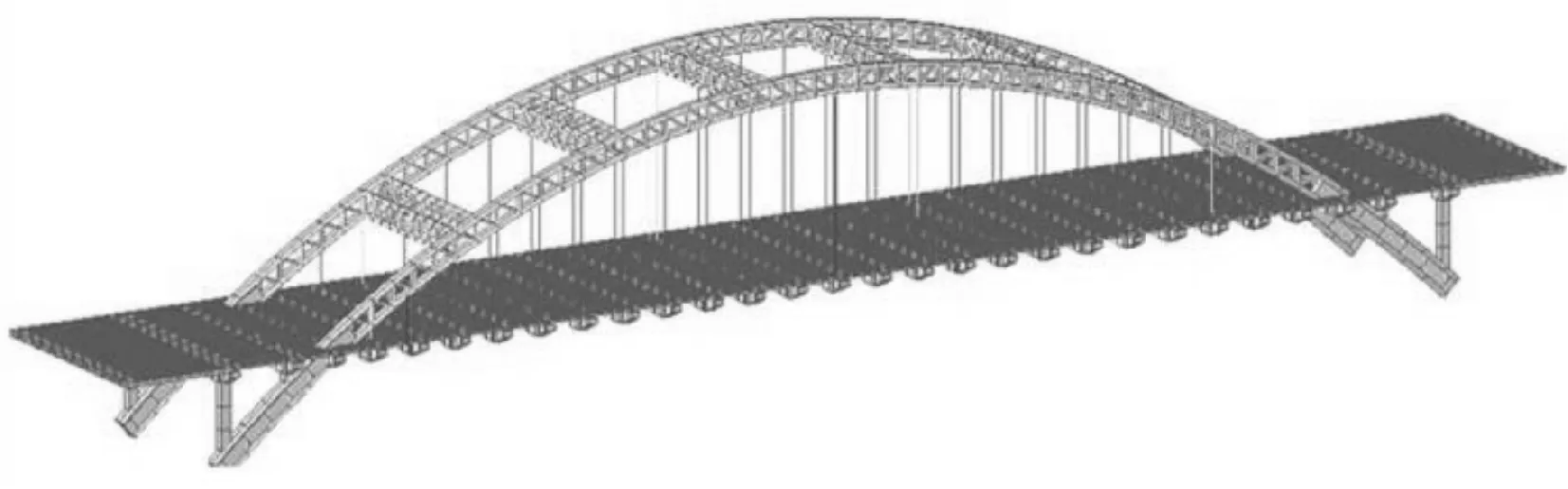
圖2 拱橋空間有限元模型

2 吊桿抗彎剛度識別

該橋吊桿構造見圖1，其高強鋼絲面積為2 709.6 mm2，鋼套管面積為1 649.3 mm2，內充砂漿面積為5 144.4 mm2，設計計算時只考慮了高強鋼絲的軸向抗拉作用，其實高強鋼絲僅占吊桿截面面積的28.5 %，而其余填充層的存在，必定將使吊桿剛度有所提高，同時具有一定的抗彎和抗剪能力。所以吊桿拉索也具有一定的抗彎剛度，但鋼絲之間既不是松散的組合，也不是完全的整體，而是介于兩者之間的狀態，其抗彎剛度難以確定。所以在分析時，有必要考慮這兩種極端的情況，即做兩種假設：一種是最小剛度假設，即假設吊桿拉索由松散的鋼絲構成，鋼絲之間沒有任何摩擦咬合，其剛度為單根鋼絲抗彎剛度之和。另一種是最大剛度假設，即假設鋼絲完全結合為一個整體，彎曲滿足平截面假定，吊桿剛度近似地認為是與拉索截面積相同的圓形截面的抗彎剛度。顯然，吊桿拉索的實際抗彎剛度介于這兩種假設之間。

吊桿計入抗彎剛度的影響時，應用經典結構動力學原理，可解得兩端固結的受拉吊桿頻率方程為[2]：

αβ(1-cosαlcoshβl)+(β2-α2)sinαlsinhβl=0

(1)

式中，

ω=2πf

其中，m為單位長度吊桿的質量，l為吊桿計算長度，f為吊桿的頻率，EI為吊桿的截面抗彎剛度。利用本方程計算吊桿拉力，只需直接將測得的某階頻率代入式中即可得出考慮抗彎剛度影響的吊桿拉力。

由于在實橋中吊桿拉力是惟一的，通過上式子，可知對應于不同頻率階數的實測吊桿拉力應該一致，據此即可識別出吊桿的實際抗彎剛度[3]，具體識別過程如下：

(1)在合理范圍內按一定步長遍取吊桿的抗彎剛度，例如，從0.1EI按0.05EI的步長取至0.9EI，其中I為按吊桿截面幾何形狀計算得到的截面慣性矩。

(2)對應于上述各個吊桿的抗彎剛度,將實測出的吊桿長度及各階振動固有頻率，代入式3.1中可以獲取對應不同頻率階數的實測索力。

(3)由于吊桿拉力唯一，不同頻率階數的實測吊桿拉力應該一致，據此即可識別出吊桿的實際抗彎剛度。

該橋于2005年實施的荷載試驗中，短吊桿頻率識別精度較差，因此選取其中5號、12號吊桿，對其抗彎剛度進行了識別，圖3、圖4給出了吊桿在不同的抗彎剛度情況下根據各階實測頻率得到的實測拉力。

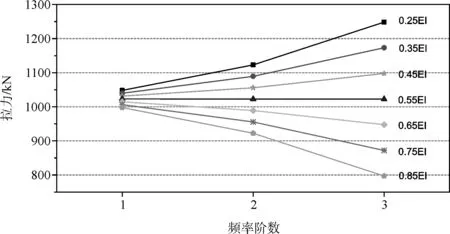
圖3 實測5號吊桿拉力

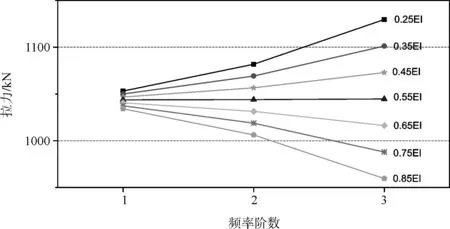
圖4 實測12號吊桿拉力

從以上兩圖可以看出，當抗彎剛度取為0.55EI時，對應各階實測頻率的吊桿拉力連線幾乎成為一根水平直線，即由各階實測頻率獲得的實測拉力幾乎相同，說明被識別吊桿的抗彎剛度應為0.55EI。事實上，吊桿的抗彎剛度屬于吊桿的內在特性，在加工工藝、各截面參數相同的情況下，不隨外因而改變。從本節選取的兩根長短不同的吊桿來看，抗彎剛度識別均為0.55EI，這也說明了吊桿抗彎剛度的取值有相同的規律性。文獻[3]利用某斜拉索不同時期的實測頻率進行了多次索抗彎剛度的識別，結果也顯示全橋斜拉索無論長短粗細，在各個時期其抗彎剛度識別結果均穩定。

以上識別結果，更長的12號吊桿，取不同的抗彎剛度其索力識別區間明顯要小于5號吊桿的索力識別區間，這也表明吊桿抗彎剛度的取值對短吊桿張力影響較大。因此，下節計算中，擬考慮長度小于10 m短吊桿的抗彎剛度影響，抗彎剛度的取值為本節中抗彎剛度識別結果0.55EI。

3 恒活載對短吊桿截面應力的影響

對長度小于10 m的1、23號短吊桿，2、22號次短吊桿計入其抗彎剛度0.55EI，在已建立好的橋梁有限元模型中，將上下游側共8根短、次短吊桿的只受拉Link10單元更換為考慮抗彎剛度的Beam188單元。

恒載作用下短吊桿內的應力主要包括軸向拉應力和彎曲正應力。圖5、圖6分別為恒載作用下上游側1、2號吊桿應力比例和應力分布。由圖可知，在恒載作用下，短吊桿內應力以軸向拉應力為主，彎曲正應力所占比例極低，基本可以忽略，這主要是因為，恒載作用主要是引起吊桿的軸向受拉變形，與吊桿的軸向受拉剛度有直接聯系，并不受抗彎剛度的影響；從兩圖中也可以觀察到，短吊桿由于抗彎剛度的影響，會導致吊桿內應力分布不均勻，但恒載作用下應力分布差別不大；短吊桿的彎曲變形主要是橫橋向的彎曲變形，這與該橋采用的橋面體系是相符合的，通過吊桿下的橫梁承擔傳遞橋面荷載。

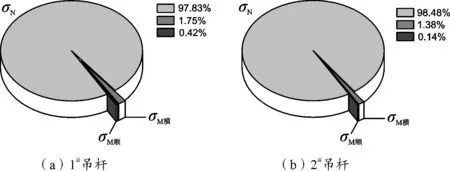
圖5 恒載作用下的上游側短吊桿應力比例

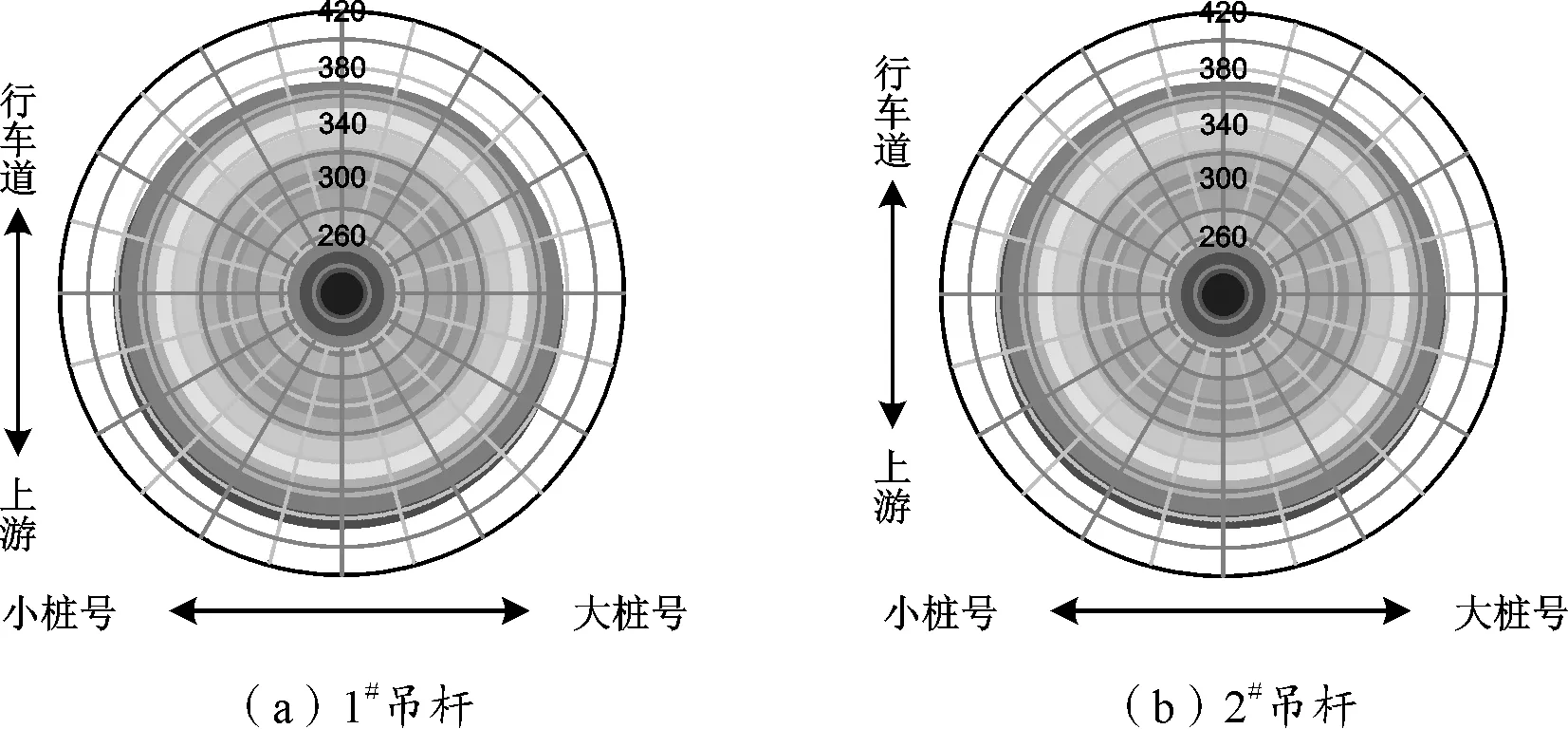
圖6 恒載作用下的上游側短吊桿應力分布(單位：MPa)

4 溫度對短吊桿截面應力的影響

考慮結構整體溫差的影響，結構整體溫差按體系降溫30 ℃計算，其位移計算結果與不考慮短吊桿抗彎剛度的結果相同，但是計入短吊桿抗彎剛度后，吊桿上下端由于橋面變形突出而產生縱向相對變形，從而在吊桿兩端產生彎矩和剪力。由于拱肋和橋面縱向變位的最大差異在短吊桿區域，致使其端部產生較大的彎矩作用，內部鋼絲受力復雜且不利，一部分處于外圍的索體拉應力增大，另一部分索體拉應力則減小，尤其最短吊桿，彎曲、剪切變形程度最大，其受力情況最為不利(圖7、圖8)。

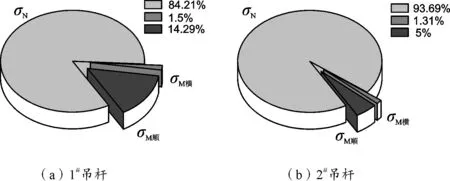
圖7 整體降溫30 ℃上游側短吊桿應力比例

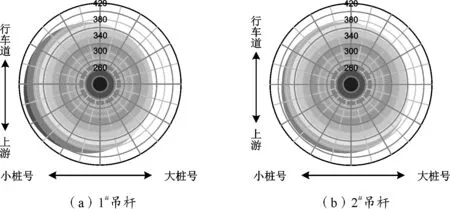
圖8 整體降溫30 ℃上游側短吊桿應力分布(單位：MPa)

從圖7、圖8可知，相對于恒載作用，整體溫度作用下，彎曲正應力效應明顯，尤其是縱向的彎曲正應力。與不考慮短吊桿抗彎剛度結果相比較，降溫30 ℃時1號短吊桿截面最大彎曲正應力達64.7 MPa，占恒載的17 %；2號次短吊桿的彎曲正應力占恒載比例分別為5.3 %。這也說明，隨著吊桿長度的增加，抗彎剛度對吊桿受力影響的逐步減弱；但是若對短吊桿不考慮抗彎剛度的影響，整體溫度作用下吊桿應力計算結果將是偏不安全的。

同時，從以上計算分析也可得知，整體溫度作用下引起的短吊桿應力不均勻分布現象非常明顯，降溫30 ℃時1號短吊桿表層鋼絲應力相差最大達到128 MPa。整體溫差作用下，拱肋由于受拱座基礎的約束，其縱向變形受到限制；而橋面兩端由于簡支在吊桿橫梁上，其縱向變形幾乎不受限制；這樣，在相同的溫差作用下，吊桿上下端由于橋面變形突出而產生縱向相對變形，從而在吊桿兩端產生彎矩和剪力。尤其短吊桿區域，內部鋼絲受力復雜且不利，一部分處于外圍的鋼絲拉應力增大，另一部分鋼絲拉應力減小，但隨到吊桿表面距離的增加，應力不均勻現象逐步減弱。

5 結論

通過吊桿的頻率方程結合實測數據，識別了該中承式拱橋短吊桿的抗彎剛度，并經過分析比較得出：在恒載作用下，短吊桿由于抗彎剛度的影響，會導致吊桿內應力分布不均勻，但恒載作用下應力分布差異不明顯；而由于抗彎剛度的影響，整體溫度作用下會引起顯著的短吊桿應力不均勻分布，導致外層鋼絲應力相差達到了100 MPa以上，這是導致短吊桿內部應力不均勻的主要因素之一。

計算分析表明，中、下承大跨拱橋的短吊桿受力較為不利，是此類橋梁中的薄弱部位，應在設計中加強對短吊桿的關注。