黏土蠕變非線性特性及其分數階導數蠕變模型

任 鵬，王 鵬，張 華，唐 印

(1. 四川省建筑科學研究院有限公司，成都 610081；2. 地質災害防治與地質環境保護國家重點實驗室(成都理工大學)，成都 610059；3. 成都大學建筑與土木工程學院，成都 610106)

黏土的蠕變具有顯著的非線性，尤其是在中-高應力條件下[1]。元件模型因為具有理論基礎完善、形式簡單、規律明確、概念清晰等優點，成為研究非線性蠕變的重要基礎。目前非線性蠕變研究主要有以下幾方面：1)傳統元件與經驗模型，孫均[1]提出采用傳統元件模型描述低應力條件下的蠕變，非線性經驗模型描述高應力條件下的蠕變，以此建立非線性蠕變模型；2)傳統元件與新型非線性元件，李晶晶等[2]通過在Burgers 模型的基礎上串聯一個非線性黏塑性元件來描述加速蠕變，建立了膨脹土的非線性蠕變模型；劉開云等[3]通過構建應變觸發式非線性黏滯元件來描述加速蠕變，并與Bingham 模型串聯，建立了三維非線性蠕變模型；韓陽等[4]通過構建一種非線性黏滯元件，分別替換Burgers 模型中的兩個黏滯元件，建立了非定常Burgers 蠕變模型；3)傳統元件與損傷非線性元件，蒲成志等[5]基于損傷理論分別構建了彈性損傷元件和黏性損傷元件，并以此與其他經典元件組合建立了五元件非線性蠕變損傷模型；謝星等[6]采用Maxwell 模型和滑塊元件并聯描述線性蠕變，構建的損傷元件描述非線性蠕變，以此建立了統計損傷蠕變模型；4)傳統元件與分數階黏滯元件，郭佳奇等[7]通過分數階微積分理論，構建了分數階黏滯元件，并利用新元件代替Kelvin-Voigt 模型中的傳統黏滯元件，建立了分數階微積分Kelvin-Voigt 模型；肖世武等[8]通過采用Koeller 彈滯元件代替標準線性固體模型中的傳統黏滯元件，建立了分數階非線性流變模型；蘇騰等[9]在Scott-Blair 分數階元件和變系數分數階元件的基礎上，建立了變階分數階非線性黏彈塑性蠕變模型。國外對非線性蠕變也有大量的研究，Chunlin[10]通過Bingham 模型和Kelvin 模型，結合損傷理論，建立了非線性黏彈塑性損傷蠕變模型；Zhu 等[11]根據試驗擬合，構建非線性化蠕變系數，并建立了非線性蠕變模型；Cao 等[12]基于損傷理論構建了一個損傷黏滯元件和損傷彈性元件，分別替換Burgers 模型中的傳統黏滯元件和彈性元件，建立了非線性損傷蠕變模型；Li 等[13]基于分數階微積分理論構建了分數階黏滯元件，并將其替換了西元模型中的兩個傳統黏滯元件，同時還基于指數函數構建了非線性黏塑性元件，將其與改進西元模型串聯，建立了非線性蠕變模型；Zhao 等[14]認為在蠕變過程中，彈性模量隨應力或時間的變化非線性軟化，而黏滯系數隨應力或時間的變化非線性硬化，并基于損傷理論、硬化理論和Burgers 模型，建立了損傷硬化非線性蠕變模型。Yang 等[15]基于損傷理論和分數階微積分理論，構建了分數階黏滯元件，建立了五元件非線性損傷蠕變模型。非線性蠕變的研究已經碩果累累，但是也存在以下問題：經驗模型理論基礎不足、地域性限制大；基于新型非線性元件、損傷理論和分數階微積分理論的蠕變模型常常因為建模元件數量較多，而引起模型參數多、形式復雜，不利于使用和推廣。因此建立一個理論基礎完善、形式簡單、概念清晰的非線性蠕變模型是非常有必要的。

本文以成都黏土為研究背景，首先展開蠕變試驗，通過分析黏土長期彈性模量和黏滯系數隨應力和時間變化的規律，明確黏土蠕變的非線性規律；其次，基于分數階微積分理論構建了分數階導數元件，基于Harris 衰減函數分別構建了非線性軟化彈性元件和非線性硬化黏滯元件，并建立了非線性分數階導數蠕變模型；最后通過非線性蠕變模型的擬合驗證分析，明確了本文蠕變模型的科學合理性。

1 蠕變試驗

1.1 試驗儀器

以成都黏土作為研究對象，進行三軸蠕變試驗，其主要物理性質參數如表1 所示。由該黏土的液塑限及含水率計算可知，天然狀態下的成都黏土處于硬塑狀態，其黏聚力和內摩擦角相對較大，表明土體力學性質相對較好。但根據成都黏土地區的實際工程經驗，成都黏土一般具有較強的水敏性及弱-中膨脹勢，其綜合力學性質復雜多變，其土體力學性質特殊性較強，具有一定的代表性。試驗儀器采用CSS-2901TS 土體三軸流變試驗機，如圖1 所示，該試驗儀器可通過應力控制的方式完成蠕變試驗。

圖1 CSS-2901TS 土體三軸流變試驗機Fig. 1 CSS-2901TS soil triaxial rheological testing machine

表1 成都黏土的基本物理性質Table 1 Basic properties of Chengdu clay

1.2 試驗方法

1)制樣，試樣尺寸為：高78 mm，直徑39.1 mm，并采用抽真空注水的方法飽和試樣。

2)裝樣及固結，對試樣施加200 kPa 的圍壓，加壓速率為0.1 kPa/min。當圍壓加壓完畢后，先關閉孔隙水壓力排水閥門，待孔隙水壓力上升至圍壓的98%以后，打開孔隙水壓力排水閥門，孔隙水壓力逐漸降低，直至孔隙水壓力消散達到95%以上，再次關閉孔隙水壓力閥門，若穩定的孔隙水壓力消散仍在95%以上，即認為試樣固結完成。

3)蠕變加載方案，蠕變試驗采用分級加載進行，加載總應力qf為333.98 kPa(qf根據《土工試驗方法標準》(GB/T 50123?2019)，由同等條件下的常規固結不排水三軸剪切試驗確定)。每級軸向加載偏應力?q=qf/x，x為加載級數(x=4)；綜上，本次蠕變試驗的加載方案為：83.49 kPa→166.98 kPa→250.47 kPa→333.96 kPa。

4)蠕變試驗每級荷載下的試樣穩定標準為變形量小于0.01 mm/2d。

2 試驗結果及分析

2.1 蠕變試驗曲線

成都黏土的蠕變時程曲線如圖2 所示。由圖2可知，成都黏土蠕變有以下特點：前三級加載時，軸向應變隨時間逐漸衰減，表現出衰減蠕變性質；第四級加載后，軸向應變先以穩定的速率變形，隨后應變速率迅速增大，直至試樣破壞，蠕變表現出一定的穩態蠕變和顯著的加速蠕變性質。

圖2 軸向應變時程曲線Fig. 2 Time history curves of the axial strain

2.2 長期強度

成都黏土的等時應力-應變曲線如圖3 所示。由圖3 可知：應力應變等時曲線出現分離，隨著時間的發展，加載瞬時的黏土應變遠小于其他時刻的應變，表現出顯著的蠕變變形。

圖3 應力-應變等時曲線Fig. 3 Isochronous stress-strain curves

其原因可能為：黏土加載的瞬時速率遠大于蠕變速率，土體力學性質表現出遠大于長期彈性模量和長期強度的瞬時彈性模量和瞬時強度，因此加載瞬時的黏土變形較小；但在恒定荷載下，隨著時間的增加，黏土力學性質表現出長期彈性模量和長期強度，其變形迅速增加，因此加載瞬時和加載后的應力應變曲線分離。第三級加載后，曲線出現拐點，根據沈明榮等[16]提出確定長期強度的等時曲線法，可將第三級軸向應力作為黏土的長期強度 σL；由于第四級軸向應力為常規三軸固結不排水確定的應力，其剪切應變速率遠大于蠕變速率，可認為黏土是“瞬時”剪切破壞的，可將第四級軸向應力作為黏土的瞬時強度。

2.3 長期彈性模量

成都黏土彈性模量EL的時程曲線如圖4 所示。由圖4 可知：在前三級加載時，EL隨著時間的增加先以較大的速率迅速衰減，隨后逐漸收斂，保持不變；最后一級加載后，EL先以某一速率穩定衰減，隨后衰減速率突增，直至土體破壞；并且EL隨著應力的增加而減小；綜上所述，EL是時間和應力的函數，隨時間和應力的增加非線性軟化。

圖4 長期彈性模量時程曲線Fig. 4 Time history curves of the long-term modulus

2.4 黏滯系數

成都黏土黏滯系數 η的時程曲線如圖5 所示。由圖5 可知： η隨著時間的增加而增加，隨著加載應力的增大而減小；在最后一級加載時， η先隨時間的增加而增加，但隨后急劇減小，直至土樣破壞。綜上所述， η是時間和應力的函數，隨時間的增加非線性硬化，隨應力的增加非線性軟化。

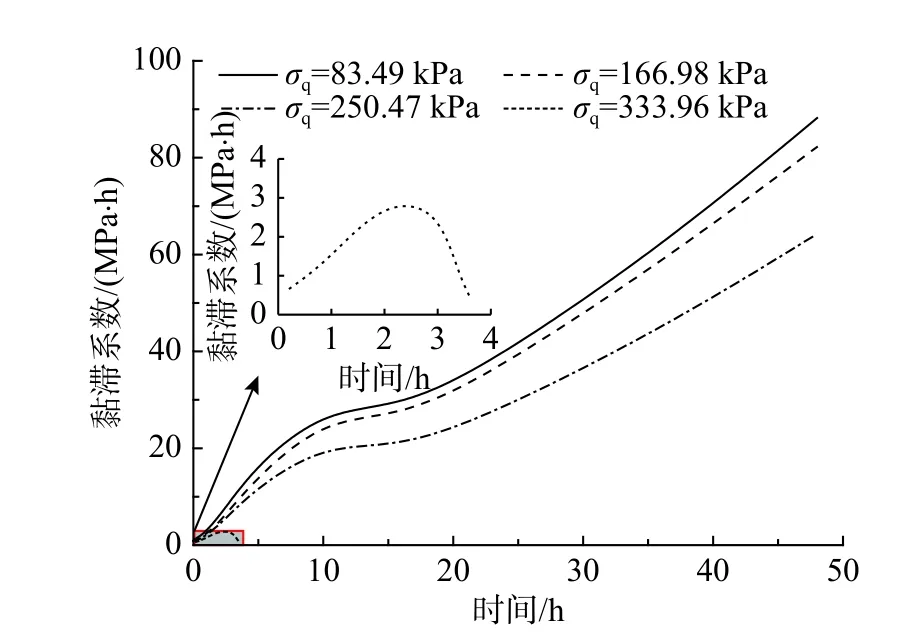
圖5 黏滯系數時程曲線Fig. 5 Time history curves of the viscous coefficient

3 非線性蠕變模型

3.1 分數階黏滯元件

元件模型雖然具有諸多優點，但其對非線性性質的描述還存在不足，而分數階算子因為對材料的歷史具有記憶性，在描述黏塑性和黏彈性時具有顯著的優勢，可很好地彌補元件模型的不足[17 ? 18]。

分數階微積分定義最常用的理論是Riemann-Liouville[19 ? 20]理論：設函數f在(0，+∞)上連續可積，對t>0 ， Re(n)≥0，分數階積分有：

式中： Γ(n)為Gamma 函數；n為分數階階數。

圖6 分數階黏滯元件Fig. 6 Fractional viscous element

3.2 非線性元件

由于Harris 函數是一種形式簡單，曲線靈活的衰減型函數[21?22]，有利于描述非線性衰減蠕變性質，因此采用該函數描述非線性衰減蠕變，其公式如下：

由式(7)建立非線性彈性元件，如圖7 所示，其本構如下：

圖7 非線性彈性元件Fig. 7 Nonlinear elastic element

2)非線性黏滯元件

由圖5 可知：黏滯系數是應力的衰減函數，是時間的增函數。因此，提出 η的非線性公式如下：

圖8 非線性黏滯元件Fig. 8 Nonlinear viscous element

3.3 非線性分數階導數蠕變模型

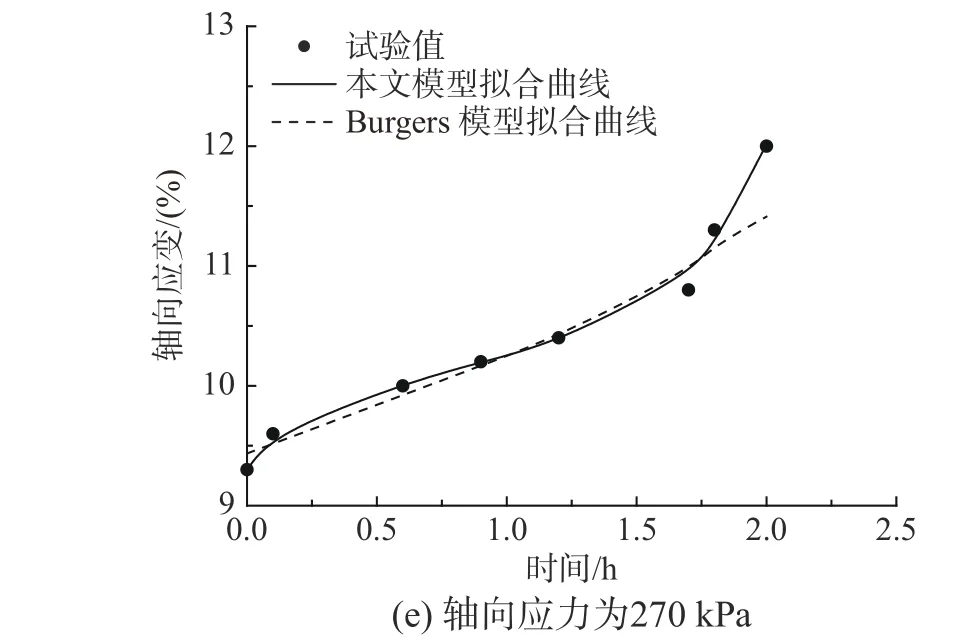
本文擬采用1 個非線性彈簧元件E、1 個非線性黏滯元件 η1、1 個分數階黏滯元件 η2和1 個塑性元件V構建蠕變模型，如圖9 所示。在圖9 中，彈簧元件描述瞬時彈性變形；當 0

圖9 非線性分數階導數蠕變模型Fig. 9 Nonlinear fractional derivative creep model

當t=0 時，在模型上施加應力 σ，黏土變形有：

4 蠕變模型辨識及性質分析

4.1 蠕變模型辨識

本文非線性分數階導數蠕變模型與經典Burgers模型類似，后者具有能較好反映瞬時應變、初始蠕變和穩態蠕變、卸載后產生塑性變形等優點[24]。因此，分別利用本文蠕變數據和文獻[25]中的蠕變數據對本文蠕變模型和經典Burgers 模型進行擬合分析。結果分別見圖10、圖11 及表2。

圖10 本文蠕變試驗擬合曲線Fig. 10 Fitting curves of creep test in this paper

由表2 可知，非線性分數階導數蠕變模型在兩個蠕變試驗第一級加載時，擬合參數ab<0，c>1 表明EL(σ,t) 、 η(σ,t)均是時間和應力的增函數，可以理解為在加載較小應力時，土體力學性質整體增強；但隨后ab>0 ， 0

各參數的建議取值區間為：在低應力條件下，a的取值區間為(0.102, 0.439)，b的取值區間為(?1.001, ?1.465)，c的取值區間為(1.599, 1.817)；在中-高級應力條件下(第二級加載以后)，a的取值區間為(?0.019, ?0.362)，b的取值區間為(?2.496,?5.629),c的取值區間為(0.271, 0.969)；n的取值區間為(7.662, 8.066)。以上各參數取值區間僅為本文對成都黏土的建議取值區間。

由圖10、圖11 可知，在低應力階段，兩個蠕變模型與蠕變試驗值的擬合度均較好，但隨著應力和時間的發展，非線性分數階導數模型與蠕變試驗值的擬合度明顯優于Burgers 模型，尤其是在加速蠕變階段。綜上所述，本文非線性蠕變模型是科學合理的，可更準確地反映黏土蠕變全過程。

圖11 文獻[25]蠕變試驗的擬合曲線Fig. 11 Fitting curves of creep tests in Reference [25]

表2 兩種蠕變模型的擬合參數Table 2 The fitting parameters of two creep models

5 結論

針對黏土蠕變的非線性性質，以成都黏土為研究背景展開了蠕變試驗；并根據試驗結果、分數階微積分理論及Harris 衰減函數，建立了非線性分數階導數蠕變模型，主要結論如下：

(1)根據成都黏土蠕變試驗結果，發現成都黏土的變形主要包括瞬時彈性變形、衰減蠕變變形、穩態蠕變變形和加速蠕變變形；長期彈性模量隨時間和應力的增加非線性軟化，黏滯系數隨應力的增加非線性軟化，隨時間的增加非線性硬化。

(2)基于分數階微積分理論和Harris 函數，分別提出了分數階導數黏滯元件、非線性彈性模量和非線性黏滯系數，并建立了模型簡單、參數少和概念清晰的非線性分數階導數蠕變模型。

(3)通過兩組蠕變試驗數據，對非線性分數階導數蠕變模型及Burgers 蠕變模型進行擬合分析，發現前者各階段的擬合系數均大于后者并大于0.99，各擬合參數的規律更明顯，對黏土非線性蠕變規律的描述更為合理，綜上所述本文建立的非線性蠕變模型是科學合理的，可更準確地反映黏土蠕變全過程。并給出了本文非線性蠕變模型各參數的建議取值區間。

應當指出，通過黏土蠕變試驗，確定彈性模量和黏滯系數的非線性特性；在流變學理論和分數階微積分理論的基礎上，構建分數階黏滯元件，非線性彈性模量和非線性黏滯系數，建立的非線性分數階導數蠕變模型，是對黏土非線性蠕變規律研究的一種嘗試和探討，但是文中只通過兩個蠕變試驗對非線性分數階蠕變模型進行辨識分析，所以蠕變模型的普適性還需要進一步驗證。