關于超可解群與Sylow塔
曾利江
(遵義師范學院 黔北文化與經濟研究院,貴州 遵義563000)
0 引言
在有限群論中,群的可解性以及超可解性[1]等都是極其重要的性質,雖然它們有區別,但也常常有聯系。正是因為人們在研究過程中發現了可解性和超可解性及其它的概念及其性質,并把它們應用于自然科學的各個分支,起到了強有力的研究工具的作用,使得群論的研究得到強大的推動力。理論研究和應用研究進入互相促進的良性循環。
研究可解性和超可解性常常需要引進一些新的概念。本文中,我們首先給出超可解群的定義,證明超可解群的幾個性質,然后引入Sylow塔的新概念,并對群的Sylow塔作了一些討論,最后我們用前面證明的超可解群的性質,證明了超可解群必有Sylow塔,并舉例說明了有Sylow塔的群不一定是超可解群。
1 一些準備
定義1.若H,K 定義2.如果有限群G的主因子均為循環群時,G就叫超可解群。 推論:超可解群的主因子不僅是循環的,實際上還是素數階的。 定理1. (1)超可解群的每個子群也超可解群; (2)超可解群的每個同態像也是超可解群; (3)兩個超可解群的直積也是超可解的; (4)若G有兩個正規子群H與K,使G/H與G/K都是超可解的,則G/H∩K也是超可解的。 證明.(1)設G為超可解群,而1=G0?G1?G2…?Gr=G為G的一個主群列,易知,對G的子群S而言有: 1=S∩G0?S∩G1?S∩G2…?S∩Gr=S 為S的一個正規群列(即每個S∩Gi為S的正規子群,見文獻[2-3]),其中商因子S∩Gi/S∩Gi-1具有性質: S∩Gi/S∩Gi-1=S∩Gi/(S∩Gi)∩Gi-1?(S∩Gi)Gi-1/Gi-1≤Gi/Gi-1, 然而對每個i,Gi/Gi-1是素數階的,故S∩Gi/S∩Gi-1或為平凡的,或為素數階的,于是從上述S的正規群列中刪掉那些重復的項以后剩下的就是S的主群列而有循環商因子,即S為超可解的。 =Gi(Gi-1N)/Gi-1N ≌Gi/Gi∩Gi-1N≌(Gi/Gi-1)/(Gi∩Gi-1N/ Gi-1) (3)設H又是一個超可解群,而有主群列1=H0?H1…?Ht=H,于是可知 1=H0?H1?…?Ht=H?G1×H?G2×H?Gr×H=G×H 為G×H的一個主群列而有循環因子Hi/Hi-1(i=1,2,…,t)及Gj×H/Gj-1×HGj/Gj-1 (j=1,2,…,r),故G×H是超可解的。 (4)設G有二個正規子群H,K使G/H與G/K都是超可解的。于是易證映射σ:g→(Hg,Kg)為G到G/H×G/K內的同態映射,且有kerσ=H∩K,故G/H∩K與G/H×G/K的一子群同構,然而(3)說明了直積G/H×G/K的超可解性,故由(1)知G/H∩K為超可解群。 先給出下面的定義,從后面可以看出Sylow塔的概念和性質用于鑒別超可解群很有用,實際上它們在自然科學的一些應用科學中都很有用。 關于Sylow塔,我們有下面幾個性質。 定理2.有Sylow塔的群必是可解群。 證明G的子群H=Gp1Gp2…Gpr-也有Sylow塔Gp1,Gp1Gp2…Gp1Gp2…Gpr-,H。故關于群的階歸納地假定H可解,則從H?G得G/H的G/H≌Gpr的可解性,從而保證了G是可解的。 定理3.當G有Sylow塔時,G的任意一組Sylowp1-,p2-,…,pr-子群也可以組成其Sylow塔,且Sylow塔是唯一的。 定理4.當G有Sylow塔時,G的子群與商群也都有Sylow塔。 證明 當H 又當G~G※時有N?G使G※≌G/N,這時易知GpiN/N為G/N的Sylowpi-子群,且不論k取1,2,…,r中任何值,恒有(Gp1N/N)(Gp2N/N)…(GprN/N)=Gp1Gp2…GprN/N?G/N,這說明G/N=G※有Sylow塔。 現在來證明超可解群與Sylow塔的一個關系,即下面的 定理5.超可解群必有Sylow塔。 證明 設G是超可解的,我們歸納地假定凡階數小于|G|的超可解群都有Sylow塔。 令p是|G|的最大素因素Gp∈Sylp(G),并令N為G的一個極小正規子群,于是有GpN/N∈Sylp(G/N),由定理1的(2),G/N是超可解的且有|G/N|<|G|,據歸納法假定有GpN/N?G/N,即GpN?G。 然而由N在G內的極小正規性以及G的超可解性有|N|=q(素數),若p=q,則GpN=Gp,故從已知的Gp?N?G即得Gp?G;若p>q,則由Sylow定理易知GpN只有唯一一個Sylowp-子群Gp是GpN的特征子群(見文獻[4-5]),再從GpN?G也得Gp?G。 總之,不論q如何,恒有Gp?G。于是|G/Gp|<|G|,故由定理1的(2),G/Gp超可解,而據歸納假設可知G/Gp有Sylow塔,因此易知G有Sylow塔。 另一方面,我們在下面的附注中指出,定理5的逆定理不成立。從而完全揭示出超可解群與Sylow塔的關系。 由上面的結果(定理5和附注)知道:超可解群必定有Sylow塔,即是說:沒有Sylow塔的群必定不是超可解群,簡單地說,有Sylow塔是一個群成為超可解群的必要條件,同時,附注說明了這個條件不是一個群成為超可解群的充分條件。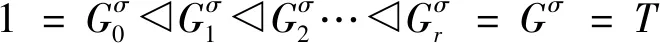
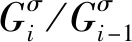
2 Sylow塔的討論
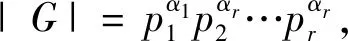
3 主要結論
4 一個附注
5 結語

