路徑規劃的可定位性研究

高 揚，劉 江，李鹍鵬

長安大學 汽車學院，西安 710054

1 引言

路徑規劃結果的實現通常高度依賴于機器人準確的定位結果。已有對路徑規劃的研究中多集中于如何根據各種條件找到一條最優的路徑，常用條件如：路徑最短、時間最優、便于執行、能夠避開障礙物等[1]。然而基于此類條件所規劃出來的路徑很少考慮到路徑的可定位性，這使得機器人在跟蹤路徑的過程中很有可能因定位誤差過大而導致路徑追蹤失敗，因此在進行路徑規劃時將可定位性考慮進來具有重要的意義。本文主要研究常見的雙輪差速機器人利用激光掃描儀，基于地圖匹配與航跡推算的定位方法，建立了兩者的定位誤差方程，分別討論了其可定位性對路徑規劃的影響[2]。

將定位的不確定性用分布的方差來描述在很多研究中都有被提到[3]。Roy最早在研究海岸線導航提出通過定位概率分布的熵值來反映機器人的可定位性[4]。Li等提出使用地圖來輔助測量定位系統提供的信息可信度[5]。Censi等人基于Cramer-Rao定理從理論上給出了基于地圖匹配定位的精度上限[6]。在Censi 等人的基礎上又發展出來一系列研究機器人可定位性估計的研究成果。Qian 等人提出了一種引入動態障礙物影響因素的定位估計方法[2]。Wang 等人提出了一種基于可定位性的機器人動作選擇機制，從而加速機器人全局定位的速度[7]。王煒等通過將概率柵格離散化，將Fisher 信息矩陣的應用擴展到概率柵格地圖中去[8]。Wang 等人基于概率柵格地圖和Cramer-Rao 邊界的激光測距模型，將先驗地圖的不確定性考慮進來，加快了機器人的定位速度[9]。孫自飛等人利用離散化Fisher信息矩陣在線估計觀測信息的可定位性矩陣，同時通過預測模型協方差矩陣評估里程計信息的可靠性，從而提高機器人的定位準確性和可靠性[10]。

近年來，也有不少研究是將機器人的可定位性考慮到路徑規劃中去。Censi 等通過計算期望激光數據以及激光掃描到的環境表面斜率，得到定位Fisher 信息矩陣，該矩陣可以反映可定位性的整體性和方向性，然而沒有考慮地圖信息的不確定性對可定位性評估的影響[11]。還有一些研究嘗試使機器人在跟蹤路徑時位置不確定性最小，但是它們要求激光的掃描范圍是360°，這就限制了其使用范圍[12-15]。Irani等通過計算LM（Localizability Measure）來排除定位性差的區域，在此基礎上再進行路徑規劃，可在一定程度上避免路徑經過可定位性差的區域，但是需要通過閾值來調整通行區域，有可能因為閾值的設置過大而大幅擴大不可通行區域[16]。

已有研究中，可定位性是如何影響路徑規劃，并且如何去衡量路徑的可定位性需要進一步地分析。因此，本文主要集中研究可定位性的影響并提出包含可定位性的新的路徑評價函數。

2 可定位性對路徑規劃的影響

2.1 基于地圖匹配和航跡推算的定位方差分析

機器人的定位結果一般來源于航跡推算和地圖匹配兩種定位方法的融合，這樣可以獲得更好的定位效果。設δm_s為基于地圖匹配得到的定位估計方差，δd_s為航跡推算所得的定位估計方差，δf_s為融合后的定位估計方差。本文建立了δd_s的估計模型如式（1）和（2）所示：

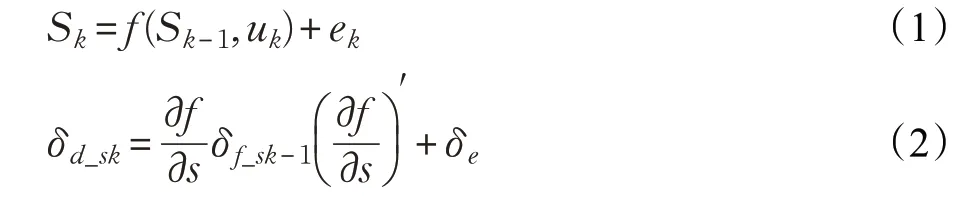
其中，f()為機器人運動方程，Sk(xk,yk,θk)為機器人當前時刻位姿，ek為機器人運動過程中所受到的噪聲，假設ek服從均值為0，方差為δe的高斯分布。當忽略機器人中不準確的運動時，δd_s可以通過式（3）計算得到：

δm_s可依據文獻[7]中方法由Fisher 信息矩陣求得其下限，如式（4）、（5）所示。riE為激光測距儀所得第i個激光束到障礙物的距離，δp為激光的白噪聲。根據Cramer-Rao 理論，則可建立對δf_s的估計，即公式（5）。由于通常將航跡推算結果與基于地圖匹配的定位結果融合使用。假設采用常用的卡爾曼濾波算法進行融合，則根據信息融合理論，δf_s可以根據公式（6）計算得到。

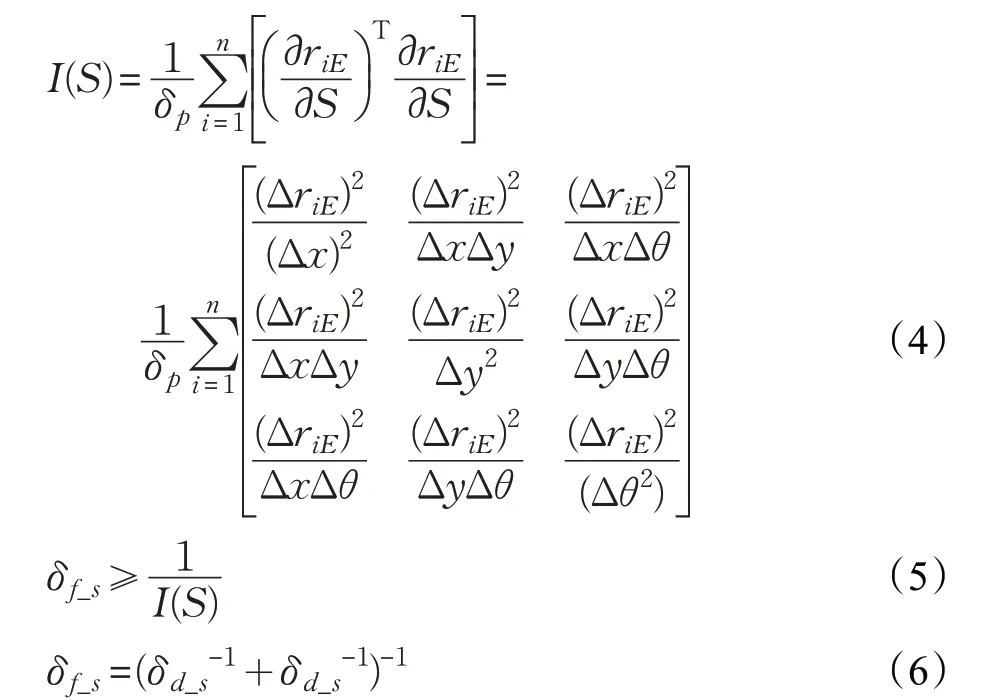
2.2 基于地圖匹配和航跡推算的定位方差分析

δf_s代表融合定位后的方差，假設定位結果服從高斯分布，則其在概率分布上呈現為一個橢球的形狀，橢球體積大小代表了機器人定位的不確定度。令δf_xy表示δf_s在X-Y平面的投影，它呈現為橢圓形狀，代表機器人位姿估計在X-Y平面上的可能的分布范圍。令δf_θ表示對機器人朝向角θ的估計。因此，δf_s可以表示為 (δf_xy,δf_θ)。如圖1 中所示，令rs為障礙物的膨脹半徑，ra為目標點的膨脹半徑，R為機器人跟蹤的路徑，‖δf_D‖為δf_xy形成的橢圓度的長軸半徑，三角形代表機器人的位姿，黑色方塊代表障礙物，藍色點為給定的路徑的預瞄點，紅色的點表示路徑終點。

圖1 定位不確定性的影響

2.3 δf_xy 和 δf_θ 對路徑規劃的影響

如圖1中所示，假設機器人真實位姿落入該橢圓形包含的范圍的概率不低于1-α，則該橢圓的長軸半徑‖δf_D‖必然滿足公式（7）：

在路徑規劃中，機器人應盡可能靠近障礙物以獲得一條最短的路徑。而‖δf_D‖越大，機器人撞到障礙物的可能性就越大，為了減少機器人碰撞的風險，‖δf_D‖應該滿足式（8）。同時為了減少由于定位不確定性導致機器人不能到達目標點的風險，‖δf_D‖還應該滿足式（9）。

對于角度誤差δf_θ對路徑規劃帶來的影響，本文分析了不同δf_θ條件下，機器人跟蹤路徑形成的軌跡長度L，如圖2所示。

圖2 不同的δf_θ 的路徑長度

分析結果表明δf_θ與L間存在如式（10）的關系：

其中X0為機器人到目標點間的起始距離，而參數p1=-6.375 ；p2=3.766E+04 ；q1=-1.436E+04 ；q2=2.669E+04。

3 定位不確定性評價函數

在路徑規劃中通常借助評價函數將優化目標映射到一個有限的值域，采用不同的路徑規劃方法，所采用的評價函數形式也不一樣。本文采用文獻[15]中提出的基于粒子濾波的全局路徑規劃方法，因而采用sigmoid函數建立可定位影響評價函數，將 ‖δf_D‖和δf_θ對路徑規劃帶來的影響映射到[0，1]。δf_s表示融合和后的定位方差，可由(δf_xy,δf_θ)表示，‖δf_D‖為δf_xy在X-Y平面投影上圓的直徑，代表了δf_s在X-Y平面上定位方差的大小，‖δf_D‖和δf_θ值越小，代表著定位方差越小，機器人的定位越準確。

3.1 δf_θ 影響的評價函數

如圖2所示，δf_θ對路徑規劃具有負面影響，所以采用的評價函數Eθ(δf_θ),如公式（11）所示：

Eθ(δf_θ)的值越小，對路徑規劃的影響更小。θu2是一個可變參數，由于當時，此時機器人到達不了終點，所以取參數k2表示評價函數值的變化速率，根據實際情況調整。其他參數本文取k2=14.1，θu2=2，因此Eθ(1)=0.5，Eθ(1.4)≈1。

3.2 ‖ δ f_D ‖影響的評價函數

由3.1 節分析可知 ‖δf_D‖對路徑安全性呈負面影響，且需滿足如式（8）、式（9）要求。故設計評價函數E(‖δf_D‖)如式（12）：

E(‖δf_D‖)的值越小，代表效果越好。其中由式（8）、（9）得到ru為由式（13）限制的最小值。

參數k1控制著評價函數值改變大小。圖3 展示了它們之間的關系，其中k1分別取0.2，0.6，1，2，3，4。k1的取值要使得E(ru)≈1。故本文取k1=1，rs=50 cm ，rR=30 cm，ra=50 cm。

圖3 在不同k 取值情況下E(‖ δ f _D ‖)和 ‖ δ f _D ‖的關系

3.3 基于可定位性的可定位性評價函數

在文獻[17]中，采用了Ferguson 樣條曲線來描述路徑R，并提出評價函數E(R,MC)來平衡路徑長度和機器人與障礙物之間的距離，E(R,MC)可由式（14）計算得知。結合本文所提出的可定性的評價函數，E(R,MC)可以擴展成新的評價函數Ep(R,MC)，如式（15）所示：

新的評價函數在路徑規劃的傳統指標與可定位性指標之間做了平衡。式（14）中MC表示環境的地圖，ELmax(R)是由式（16）求得的路徑R的最大可定位評價值，ES(S)是給定路徑點S的可定性評價值。L是由式（17）定義的路徑R長度，lmin是起點P0到目標點Ta的最短距離。dmin為路徑R到障礙物的最短距離，由式（18）求得，α1是一個權重系數。Xi(T)、Yi(T)為曲線i在X-Y平面的坐標，Xi′(T)、Yi′(T)為對T的導數。objx和objy為X-Y坐標系中距離原點最近的障礙物的坐標。α1,α2,α3是影響dmin,‖δf_D‖以及δf_θ的三個權重參數。

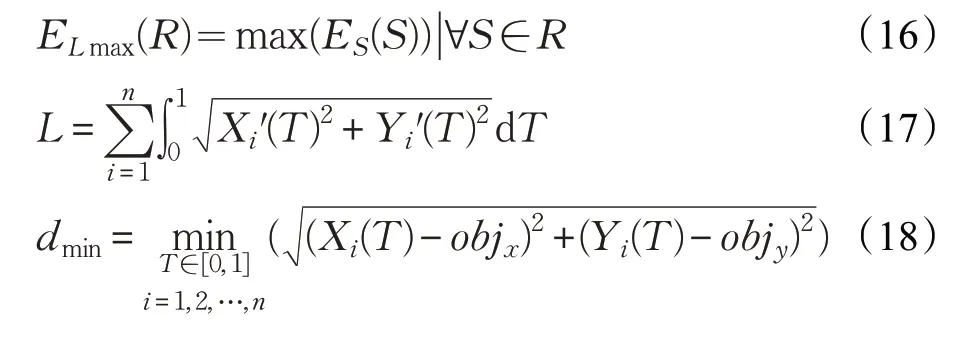
4 實驗結果分析

為了驗證本文所提出算法的效果，在圖4（a）所示的室內環境進行了實驗，圖4（b）為實驗所用概率柵格地圖。實驗機器人采用先鋒機器人Pioneer 3-DX，如圖5所示配置了里程計和激光測距儀（UTM-30LX）。控制器采用戴爾電腦，系統為Ubantu16.04，內存為8 GB。算法設置參數如下：激光掃描距離：Ld=3 m ，掃描范圍[0°，270°]，激光束數目n=1 080 ，掃描周期T=25 ms。

圖4 實驗場地

圖5 Pioneer 3-DX機器人

圖6中紅色的實線是傳統的路徑規劃路線，藍色的實線是加入了本文提出的路徑評價函數生成的優化路徑。在實驗過程中機器人采用自適應粒子濾波定位的方法實現自定位，圖6 中虛線代表機器人真實的軌跡。機器人在跟隨傳統路徑時，由于穿行的區域定位誤差過大，在實驗過程中丟失了自己的位姿，不能成功地到達終點，而機器人在跟隨本文改進后優化的路徑，穿過的路徑區域可定位性比較好，成功地到達終點。

圖6 優化后的路徑以及傳統路徑

圖7展示了機器人在跟隨優化后的路徑時本文設計的四種可定位性評價指標(‖δf_D‖,δf_θ,E(‖δf_D‖),Eθ(δf_θ))的變化，‖δf_D‖其中代表δf_xy形成的橢圓度的長軸半徑，δf_θ代表朝向角的方差，E(‖δf_D‖)代表 ‖δf_D‖的評價函數值，Eθ(δf_θ)代表δf_θ評價函數值。

圖7 優化路徑的四種評價指標變化

圖8 展示了機器人在跟隨傳統路徑時四種評價指標的變化。可以明顯看到在跟隨優化后的路徑時四種評價指標的值比較小，這使得機器人可以成功地到達目的地。相反機器人在跟隨傳統路徑時，從第75 處定位到115處定位，由于δf_θ比較大，使得機器人由于定位誤差比較大而不能達到終點。

5 結束語

本文主要研究定位不確定性對路徑規劃和路徑跟蹤的影響。通過將定位的不確定性分解為坐標定位方差和朝向角估計方差降低了可定位性評估難度。分析了兩者對機器人路徑跟蹤的影響，在此基礎上，提出了一個評價函數來評價不確定性對路徑規劃影響。實驗表明，評價函數成功地描述了不確定性的影響，使得機器人在進行路徑規劃時可以在傳統指標與可定位性指標間取得平衡。

圖8 傳統路徑的四種評價指標變化