三支決策樸素貝葉斯增量學習算法研究

韓素青，成慧雯，王寶麗

1.太原師范學院 計算機科學與技術(shù)系，山西 晉中 030619

2.運城學院 數(shù)學與信息技術(shù)學院，山西 運城 044000

1 引言

1973 年，Duda 和Hart 基于貝葉斯公式首次提出了樸素貝葉斯分類模型（Na?ve Bayes Classifiers，NBC），該模型由于實現(xiàn)簡單，計算高效，并具有堅實的理論基礎(chǔ)而得到廣泛應(yīng)用。近年來，隨著數(shù)據(jù)的爆炸式增長以及流數(shù)據(jù)的不斷涌現(xiàn)，包括樸素貝葉斯算法在內(nèi)的許多分類算法的泛化性和可擴展性受到了限制。

增量式學習能夠利用增量數(shù)據(jù)中的有用信息通過修正分類參數(shù)來更新模型，它有兩個顯著的特點：（1）無需存儲歷史數(shù)據(jù)；（2）能夠有效利用之前的訓練結(jié)果。因此，增量式學習被視為處理大規(guī)模數(shù)據(jù)和流數(shù)據(jù)的一類有效方法。

貝葉斯學習本身具有增量學習的特性，不僅易于實現(xiàn)增量學習的功能，而且可以有效降低學習算法的復雜性。最早提出的增量貝葉斯學習模型[1]，根據(jù)0～1 損失[2]，通過依次加入能夠最小化當前分類模型分類損失的樣本，以增量方式學習分類參數(shù)，并實現(xiàn)對樣本的分類。但該算法在增量過程中，易受噪聲影響。為此，一些學者對其進行了改進。丁厲華等人[3]以類支持度因子選擇增量樣本來對分類器進行更新，但該算法降低噪聲影響的效果并不明顯。羅福星等[4]提出一種加權(quán)樸素貝葉斯增量學習算法，該算法基于置信度，動態(tài)調(diào)整增量樣本，具有良好的自適應(yīng)能力。不過，由于該算法對部分頻數(shù)較少但卻具有較強分類能力的樣本的偏好不足，因此可擴展性不強。

姚一豫教授于2010年創(chuàng)立的三支決策理論是符合人類認知模式的一種新型理論。該理論從應(yīng)用的角度對粗糙集的核心概念正域、負域和邊界域給出了合理的語義解釋[5-6]。有別于傳統(tǒng)二支決策理論只考慮接受和拒絕兩種選擇，三支決策理論在解決很多問題時，會依據(jù)決策可能導致的代價或后果，增加延遲決策這一選擇。當信息不足，難以決定接受或者拒絕時，采取延遲決策，不僅可以減少對不確定性知識做出誤判，而且能夠規(guī)避誤判所導致的損失，符合人們在決策過程中的思維習慣。

近年來，關(guān)于三支決策的研究受到越來越多學者的關(guān)注，劉盾等對三支決策理論提出了新的研究方法和應(yīng)用領(lǐng)域[7]；杜麗娜等將貝葉斯原理和基于決策粗糙集的三支決策規(guī)則引入到模糊綜合評判中，提出了基于三支決策風險最小化的風險投資評判模型[8]；李華雄等采用代價敏感三支決策方法獲得了相應(yīng)粒度下的最小代價決策[9]；李金海等提出了一種用多粒度描述三支決策概念的公理化方法，并通過數(shù)值實驗對所提出的學習方法進行了性能評價[10]；郎廣名等在決策粗糙集理論的基礎(chǔ)上，提出了動態(tài)信息系統(tǒng)中概率沖突集、中性集和聯(lián)合集的增量構(gòu)造方法[11]；此外，李金海等還對概念格與三支決策相結(jié)合的研究進行了一定的探討及展望[12]。

由于三支決策粗糙集模型傾向于關(guān)注分類錯誤帶來的風險代價，因此是具有代價敏感性數(shù)據(jù)分析的有效工具[13]。此外，三支決策理論中損失函數(shù)的確定需要先驗信息和專家知識，存在一定的主觀能動性，與樸素貝葉斯學習的客觀性某種程度上形成了互補。

本文將三支決策思想融入樸素貝葉斯增量學習中，提出一種基于三支決策的樸素貝葉斯增量學習算法。首先，為防止有用信息過早損失，利用樸素貝葉斯算法得到的最大后驗概率和次最大后驗概率構(gòu)造了一個稱為分類確信度的評價函數(shù)，用以確定三支決策理論中的正域、負域和邊界域。然后算法以迭代方式進行，每一次迭代都用由正域、負域中的誤分類樣本、邊界域中的樣本以及新增樣本構(gòu)成的數(shù)據(jù)集重新訓練樸素貝葉斯分類器，直到算法結(jié)束。三支決策思想的引入和增量學習機制的構(gòu)建，旨在使算法的分類正確性和召回率獲得明顯提高。

2 基本概念

2.1 樸素貝葉斯分類模型

樸素貝葉斯模型結(jié)構(gòu)簡單、計算高效、易于闡釋且應(yīng)用廣泛。但該模型需要一個很強的條件保證，即需要假定描述數(shù)據(jù)的各個屬性對于給定類的取值相互獨立，即任何屬性的取值不依賴于其他屬性。

假定數(shù)據(jù)集D包含m個條件屬性，記作A1,A2,…,Am；以及t個類，記作C1,C2,…,Ct。訓練樣本X表示為一個m維特征向量，即X={x1,x2,…,xm} ，其中xi表示樣本關(guān)于條件屬性Ai的值，則貝葉斯原理描述如下：

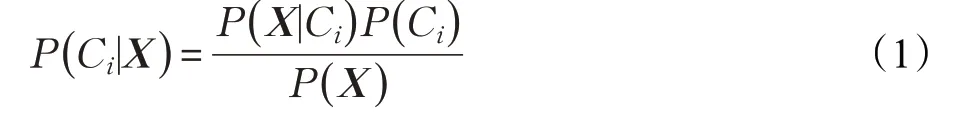
其中，P(Ci)為代表各類樣本在樣本集中所占比例的先驗概率；P(X|Ci)為樣本X相對于類Ci的條件概率；P(Ci|X)為樣本X屬于類Ci的后驗概率；而P(X)是則是用于歸一化的“證據(jù)”因子。

給定樣本X，樸素貝葉斯分類器將X預測為具有最大后驗概率P(Ci|X)的類，即樸素貝葉斯分類器將樣本X分配給類Ci，當且僅當：

在貝葉斯公式（1）中，由于分母P(X)與類標號的取值無關(guān)，因此在確定類別時可以作為常數(shù)處理。這樣最大化后驗概率P(Ci|X)的計算就可以轉(zhuǎn)換為P(X|Ci)P(Ci)的計算。于是，根據(jù)樸素貝葉斯分類的條件獨立性假設(shè)可得：

其中，P(x1|Ci)×P(x2|Ci)×…×P(xm|Ci)可以從數(shù)據(jù)集中求得。于是，樸素貝葉斯分類模型描述為：

2.2 樸素貝葉斯增量學習算法

增量分類學習的實質(zhì)可以歸結(jié)為根據(jù)先驗知識和增量信息來確定先驗概率P(Cj)和條件概率P(X|Cj)。增量式貝葉斯分類主要針對增量樣本集T={T1,T2,…,Tr}進行處理，可以分兩種情況進行討論。

（1）增量集T中的每一個樣本都擁有類別標簽。這種情況下，增量學習先用當前分類器對T中的樣本進行測試，并將測試結(jié)果與其本身的類別標簽進行對比，若結(jié)果一致，則保持當前分類器不變；否則用新增樣本修正當前分類器。

（2）增量集T中的每一個樣本都沒有類別標簽，需要先用當前分類器為每個樣本分配類標簽，然后再利用其含有的有用信息更新當前分類器。

無論是情況（1）還是情況（2），增量學習更新分類參數(shù)都應(yīng)當從增量集T中優(yōu)先選擇能夠有效提升分類器精度的有價值的樣本。

假定樸素貝葉斯增量學習采用0～1 損失[2]度量性能，并假定增量樣本Tp(Tp∈T,p=1,2,…,r)根據(jù)樸素貝葉斯分類器獲得的類標簽為(p=1,2,…,r)，則根據(jù)文獻[1]：

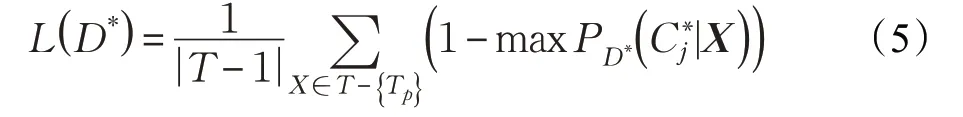
算法1一種增量貝葉斯分類模型[1]

輸出：增量貝葉斯分類器C。

步驟1利用訓練集D，學習樸素貝葉斯分類器C。

步驟2如果T=φ，返回樸素貝葉斯分類器C；否則轉(zhuǎn)步驟3。

步驟3令分類損失l=0，對增量集T中的每一個樣本Tp∈T，重復以下步驟：

（1）利用現(xiàn)有分類器C、分類Tp，獲得Tp的類標簽。

（3）如果L＞l則。

步驟4。

轉(zhuǎn)步驟1。

上述增量貝葉斯分類模型有兩個點非常關(guān)鍵：一是對增量樣本進行分類；二是基于新增數(shù)據(jù)后的數(shù)據(jù)集計算類概率P?(Ci)：

和類條件概率P?(xjd|Ci)：

其中，在式（6）中，μ=|C|+|D|，|C|為類別數(shù)，|D|為訓練樣本的大小。在式（7）中λ=|Aj|+count(Ci)，|Aj|為屬性Aj取值的個數(shù)，count(Ci)是類別為Ci的樣本個數(shù)，xjd為屬性Aj的第d個取值。

2.3 三支決策

姚一豫教授提出的三支決策理論[6，14-15]研究的最初目的是為粗糙集的三個域提供合理的語義解釋。他將粗糙集中的正域、負域和邊界域分別對應(yīng)于決策中的接受、拒絕和不承諾。具體而言，正域?qū)?yīng)于可以接受的決策，負域?qū)?yīng)于應(yīng)當拒絕的決策，而邊界域則對應(yīng)于不承諾的決策。做出接受、拒絕或不承諾三種決策需要考慮決策所導致的風險或代價[2]。在三支決策理論中，決策的代價函數(shù)或風險函數(shù)可以作為評價函數(shù)用于確定三支決策理論中的正域、負域和邊界域。因此，三支決策理論中的正域、負域和邊界域與代價函數(shù)或風險函數(shù)密切相關(guān)。

假定D是一個有限、非空的樣本集或決策方案集，A是由有限個條件組成的條件集，其中條件集可能包含指標、目標或約束。決策的主要任務(wù)是根據(jù)給定的條件集A，對每個樣本X∈D做出決策。

如果令α和β(β＜α)是以樣本的某個決策風險函數(shù)或決策代價函數(shù)為評價函數(shù)獲得的閾值，那么對于給定的條件集A，三支決策理論針對D中樣本滿足給定條件的程度，可以處理D中樣本的分類問題，并作出合理的決策[7]：

（1）如果樣本X滿足給定條件的程度大于或等于閾值α，那么認為該樣本符合給定的條件，應(yīng)做出接受的決策。

（2）如果樣本X滿足給定條件的程度小于或等于閾值β(β＜α)，那么認為該樣本不符合給定的條件，應(yīng)做出拒絕的決策。

（3）如果樣本X滿足給定條件的程度介于α和β之間，那么認為該樣本難于判斷是否符合給定的條件，應(yīng)做出不承諾的決策。

于是，基于確定的閾值α、β(β＜α)，所有樣本可以根據(jù)其評價函數(shù)值的大小被劃分到三支決策理論的正域、負域或邊界域中。

3 基于三支決策的樸素貝葉斯增量學習算法

樸素貝葉斯增量學習算法，對于樣本的類別通常有明確的判斷，但是在實際情況中，經(jīng)常會有因各種因素難于對樣本類別進行明確判斷的情況出現(xiàn)，本章將三支決策思想應(yīng)用于一般樸素貝葉斯增量算法中，研究基于三支決策的樸素貝葉斯增量學習算法。

基于三支決策的樸素貝葉斯增量學習算法的主要思路如下：

在判別信息不足，難于將待分類樣本正確分類時，利用三支決策思想，先把這些樣本劃分到邊界域中，等判別信息量足夠時，再將待分類樣本正確分類到所屬類別中。

3.1 分類確信度

樸素貝葉斯分類方法基于最大后驗概率對樣本進行分類，也就是說，對于待分類樣本，樸素貝葉斯算法根據(jù)其最大后驗概率確定其類別標簽CNB。

對于待分類樣本X，在其所有類別的后驗概率中，如果最大后驗概率和次最大后驗概率的值非常接近，那么可以認為，將樣本X賦予最大后驗概率所確定的類別的確信度不足。基于這種考慮，分類確信度定義如下。

定義1分類確信度。給定訓練集D，由訓練集D得到的樸素貝葉斯分類器記作NBC,則對于任意X∈D，樣本X屬于其最大后驗概率所確定類別的分類確信度為：

其中，P(yfirst|X,NBC)和P(ysecond|X,NBC)分別為樣本X根據(jù)樸素貝葉斯分類器獲得的最大后驗概率和次最大后驗概率。

這里，將最大后驗概率和次最大后驗概率的差值與最大后驗概率作比是為了將分類確信度的值歸一化到0～1之間。

易知，樣本X屬于其最大后驗概率所確定的類別的分類確信度Ccertainty越大，樣本X被正確分類的可能性越大。

3.2 基于分類確信度的正域、負域和邊界域

本節(jié)以3.1 節(jié)定義的分類確信度Ccertainty為評價函數(shù)定義訓練集的正域、負域和邊界域，閾值(α,β)根據(jù)所有樣本的分類確信度確定。于是，對于確定好的閾值(α,β)，訓練集D′?D的正域、負域和邊界域的判別規(guī)則可定義如下：

（1）若Ccertainty(X)≥α，則X∈POS(D′ )；

（2）若β ＜Ccertainty(X)＜ α，則X∈BND(D′ )；

（3）若Ccertainty(X)≤β，則X∈NEG(D′ )。

下面給出基于三支決策的樸素貝葉斯的邊界域的提取算法。

算法2基于分類確信度的邊界域提取算法

輸入：訓練集D={X1,X2,…,Xn} ，訓練集D的類別Cj(j=1,2,…,t)，閾值參數(shù)α和β。

輸出：D中基于分類確信度的邊界域EB。

步驟1在D上訓練樸素貝葉斯分類器NBC。

步驟2對D中的每一個樣本Xi(i=1,2,…,n)重復：

（1）對j=1,2,…,t，根據(jù)NBC計算其后驗概率P(Cj|Xi)。

（2）根據(jù)公式（8）計算其分類確信度Ccertainty(Xi)。

步驟3確定閾值(α,β)。

步驟4根據(jù)閾值α和β，確定D中的邊界域EB。

步驟5輸出EB。

步驟6算法結(jié)束。

3.3 基于三支決策的樸素貝葉斯增量學習算法

在對有類別標簽的數(shù)據(jù)集進行學習并更新分類器時，文獻[16]認為被當前分類器錯分的樣本中蘊含著比分對的樣本更多更有用的信息。因此將基于分類確信度確定的正域、負域中的誤分樣本通過類別標簽索引[17]分別提取并作為增量數(shù)據(jù)使用，有助于分類器性能的提升。

算法3基于三支決策的樸素貝葉斯增量學習算法

輸入：訓練集D，隨機等分為N個互不相交的子集Di(i=1,2,…,N)。

輸出：基于樣本集D的樸素貝葉斯分類器Γ。

步驟1取訓練集D1進行訓練，得到初始的樸素貝葉斯分類器NBC1。

步驟2根據(jù)算法2，以及閾值α和β，找出訓練集D1中的邊界樣本集EB1。

步驟3通過類標簽索引提取D1中對應(yīng)的正域、負域中的誤分樣本MC1。

步驟4將EB1、MC1和子集D2的并集作為新的訓練樣本訓練新分類器NBC2。

步驟5重復步驟2，將得到的新的EBi、MCi和子集Di+1合并訓練，如此循環(huán)，直至獲得由EBN-1、MCN-1與DN訓練所得到的NBC，并將其作為最終分類器Γ輸出。

步驟6算法結(jié)束。

該算法主要利用三支決策思想具有代價敏感性的優(yōu)勢，通過引入一種分類確信度作為評價函數(shù)進行三支決策劃分，采取比一般樸素貝葉斯增量算法更加謹慎的態(tài)度，避免了有用信息的過早損失。

3.4 算法時間復雜度分析

對于算法1 所示的一種增量貝葉斯分類模型的時間復雜度主要取決于樸素貝葉斯分類學習模型的訓練和分類損失的計算。在步驟1中，訓練集的時間復雜度為O(smt)，其中s為訓練樣本數(shù)，m為屬性數(shù)，t為類別數(shù)。在步驟3中，由于樸素貝葉斯增量學習可以利用原始的訓練結(jié)果，故增量樣本集的時間復雜度為O(hr2mt)，其中h為屬性取值的最大個數(shù)，r為增量集的個數(shù)。所以算法1的時間復雜度為O[(s+hr2)mt]。

對于算法2 所示的基于分類確信度的邊界域提取算法的時間復雜度主要取決于樸素貝葉斯分類學習模型的訓練和分類確信度的計算。即主要取決于步驟2，故訓練集的時間復雜度為O(nmt)，其中n為訓練樣本數(shù)，m為屬性數(shù)，t為類別數(shù)。所以算法2 的時間復雜度為O(nmt)。

對于算法3 所示的基于三支決策的樸素貝葉斯增量學習算法的時間復雜度主要取決于樸素貝葉斯分類學習模型的訓練和算法2 中對邊界域的提取。該算法將訓練集隨機等分為N個互不相交的子集，并假設(shè)每個子集的個數(shù)為k。在步驟2中，需要對每個子集計算其類概率P(Cj)以及類條件概率P(Cj|Xi)，因此其時間復雜度為O(kmt)，其中m為屬性數(shù)，t為類別數(shù)。因此算法3的時間復雜度為O(Nkmt)。

經(jīng)分析可知，雖然本文提出的算法3中邊界域的樣本數(shù)由閾值α、β確定，但訓練集中對應(yīng)的正域、負域中的誤分樣本是通過類標簽索引提取的；而算法1中分類損失的計算是一個循環(huán)的過程。因此，一般情況下，對于確定的閾值α、β，本文提出的算法3會比算法1的時間復雜度在一定程度上有所降低。

4 實驗設(shè)計與結(jié)果分析

4.1 實驗數(shù)據(jù)與實驗環(huán)境

實驗數(shù)據(jù)使用UCI 數(shù)據(jù)庫中[18]如表1 所示的數(shù)據(jù)。實驗環(huán)境為：IntelLenovoi7-4790CPU，4 GB 存儲，Windows 7系統(tǒng)，Matlab 2014aMyEclipse。

表1 實驗使用的UCI數(shù)據(jù)集

4.2 實驗設(shè)計及結(jié)果分析

實驗需要先對所選數(shù)據(jù)集進行預處理，當存在缺失值的樣本在整個數(shù)據(jù)集中占比很小的，從數(shù)據(jù)集中刪除存在缺失值的樣本，當存在缺失值的樣本在整個數(shù)據(jù)集中占比較大時，采用均值填充法對缺失值進行處理。實驗過程中，為保證評估結(jié)果穩(wěn)定可靠，每個數(shù)據(jù)集都調(diào)用隨機函數(shù)將其隨機劃分為兩個部分：第一部分由80%的數(shù)據(jù)構(gòu)成，作為訓練數(shù)據(jù)集使用。使用過程中，這部分數(shù)據(jù)又被平均分成5 份依次進行增量學習。另一部分由其余20%的數(shù)據(jù)構(gòu)成，作為測試數(shù)據(jù)使用。

實驗采用5折交叉驗證，通過交替對換訓練集與測試集實現(xiàn)，并以5次實驗結(jié)果的均值作為終值使用。

注解：（1）由于訓練集不完備會造成后驗概率出現(xiàn)0的現(xiàn)象，故實驗過程中采用拉普拉斯對數(shù)據(jù)進行了平滑修正。（2）本文提出的算法與閾值參數(shù)α、β的選擇相關(guān)，其值通常介于[0，1]之間，需要根據(jù)具體問題通過選擇相應(yīng)的損失函數(shù)獲得[14-15，19-25]。

為分析α、β取不同值時對應(yīng)結(jié)果的變化，本文在[0，1]之間以 0.1 為漸進度選取不同的α和β進行實驗。實驗結(jié)果根據(jù)分類準確率和召回率進行評價。

分類準確率記作CA，定義如下：

其中，a表示測試數(shù)據(jù)集中被正確分類的數(shù)據(jù)個數(shù)，Ntest表示測試數(shù)據(jù)的總數(shù)。

召回率記作recall，是待測試數(shù)據(jù)集中某類樣本被正確分類的樣本數(shù)與該類所有樣本數(shù)的比值，即

其中，yi表示樣本xi的實際類別，f(xi)為分類器，是分類器f(xi)對測試樣本xi的分類結(jié)果，I(?)為示性函數(shù)，count(yi)為測試集中類別為yi的樣本總數(shù)。

對于示性函數(shù)I(?)，如果f(xi)=y′i且y′i=yi，則示性函數(shù)的取值為1，否則取值為0。

首先，針對分類準確率，基于表1所示數(shù)據(jù)，比較基于三支決策的樸素貝葉斯增量學習算法與本文算法1所示的一種增量貝葉斯分類模型的測試結(jié)果。

基于三支決策的樸素貝葉斯增量學習算法關(guān)于表1所示9 個數(shù)據(jù)集在不同α、β閾值參數(shù)下的實驗結(jié)果如圖1～圖9所示。其中，α的取值為X軸，β的取值為Y軸，分類準確率為Z軸。

由圖1～圖9可知，當α≤β時，即當α與β的取值位于X正半軸與Y正半軸所形成區(qū)域45°對角線的左半部分時，樣本集中不存在邊界樣本，所以基于三支決策的樸素貝葉斯增量學習算法的測試結(jié)果與一種增量貝葉斯分類模型的測試結(jié)果相同。當α ＞β時，即當α與β的取值位于X正半軸與Y正半軸所形成區(qū)域45°對角線的右半部分時，邊界域存在，此時基于三支決策的樸素貝葉斯增量學習算法的測試結(jié)果與一種增量貝葉斯分類模型的測試結(jié)果相異，具體情況分析如下。

為描述簡單，下面將算法1所示的一種增量貝葉斯分類模型記為算法A，本文提出的基于三支決策的樸素貝葉斯增量學習算法記為算法B。

由圖1～圖3可知，當α ＞β時，邊界域存在，此時，關(guān)于數(shù)據(jù)集 Breast-cancer、Haberman's Survival 和 Bupa，算法B 的分類準確率總體上優(yōu)于算法A 的分類準確率。說明在α、β取值合適的情況下，可以保證算法B優(yōu)于算法A。

圖1 Breast-cancer數(shù)據(jù)集測試結(jié)果

圖2 Haberman's Survival數(shù)據(jù)集測試結(jié)果

圖3 Bupa數(shù)據(jù)集測試結(jié)果

圖4 Balance-scale數(shù)據(jù)集測試結(jié)果

圖5 Tic-Tac-Toe數(shù)據(jù)集測試結(jié)果

圖6 Contraceptive Method Choice數(shù)據(jù)集測試結(jié)果

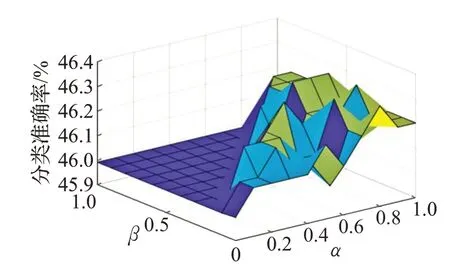
圖7 Mammographic Mass數(shù)據(jù)集測試結(jié)果

圖8 Chess（KR-VS-KP）數(shù)據(jù)集測試結(jié)果

圖9 Dermatology數(shù)據(jù)集測試結(jié)果

由圖4～圖7可知，當α ＞ β時，邊界域存在，此時，關(guān)于數(shù)據(jù)集Balance-scale、Tic-Tac-Toe、Contraceptive Method Choice 和 Mammographic Mass，算法 B 的分類準確率全部大于算法A 的分類準確率，說明只要α、β滿足α ＞β，算法B 就一定優(yōu)于算法 A。

由圖8可知，當α ＞β時，邊界域存在，此時，關(guān)于數(shù)據(jù)集Chess（KR-VS-KP），算法 B 的分類準確率總體上優(yōu)于算法A 的分類準確率，且分類準確率大多集中在90%左右。特別地，當α取0.9，β取0時，分類準確率高達93.84%，比算法A 提高了9.64 個百分比。說明在α、β取值合適的情況下，可以保證算法B遠遠優(yōu)于算法A。

由圖9可知，當α ＞β時，邊界域存在，此時，關(guān)于數(shù)據(jù)集Dermatology，算法B 的分類準確率均優(yōu)于算法A的分類準確率，特別地，當α取1.0，β取0.2 時，分類準確率高達98.05%，比算法A 提高了6.69 個百分比。說明在α、β取值合適的情況下，也可以保證算法B 遠遠優(yōu)于算法A。

表2是選取不同α、β值時，算法A 和算法B 分類準確率的對比結(jié)果。結(jié)果進一步顯示，在α、β值選擇合適時，相較于算法A，算法B的分類準確率有了明顯的提高。

面對實際問題時，α和β需要針對具體問題選擇合適的評價函數(shù)來求得相應(yīng)的閾值。

綜上所述，當α ＞ β，且α和β的取值合適時，本文提出的基于三支決策的樸素貝葉斯增量算法的分類準確率明顯優(yōu)于算法1所示的增量貝葉斯分類模型。

其次，由于數(shù)據(jù)集類別不平衡現(xiàn)象普遍存在，因此僅用分類準確率來衡量模型的性能可能存在片面性，因此基于召回率，根據(jù)表1 所示數(shù)據(jù)集，本文對算法A 和算法B 進行了二次比較分析。

在表1 所示數(shù)據(jù)集中，Breast-cancer、Haberman's Survival、Balance-scale 和 Dermatology 是 4 個不平衡數(shù)據(jù)集，圖10～圖13是算法B 基于4個數(shù)據(jù)集在不同閾值參數(shù)下的實驗結(jié)果，其中α的取值為X軸，β的取值為Y軸，分類召回率為Z軸。

觀察圖10～圖13易知，當α≤β時，數(shù)據(jù)集中不存在邊界樣本，故算法B 的召回率與算法A 的召回率相同；當α ＞β時，數(shù)據(jù)集中存在邊界樣本，且當α、β取值合適時，算法B 關(guān)于每個數(shù)據(jù)集的各個類別的召回率均比算法A 高。

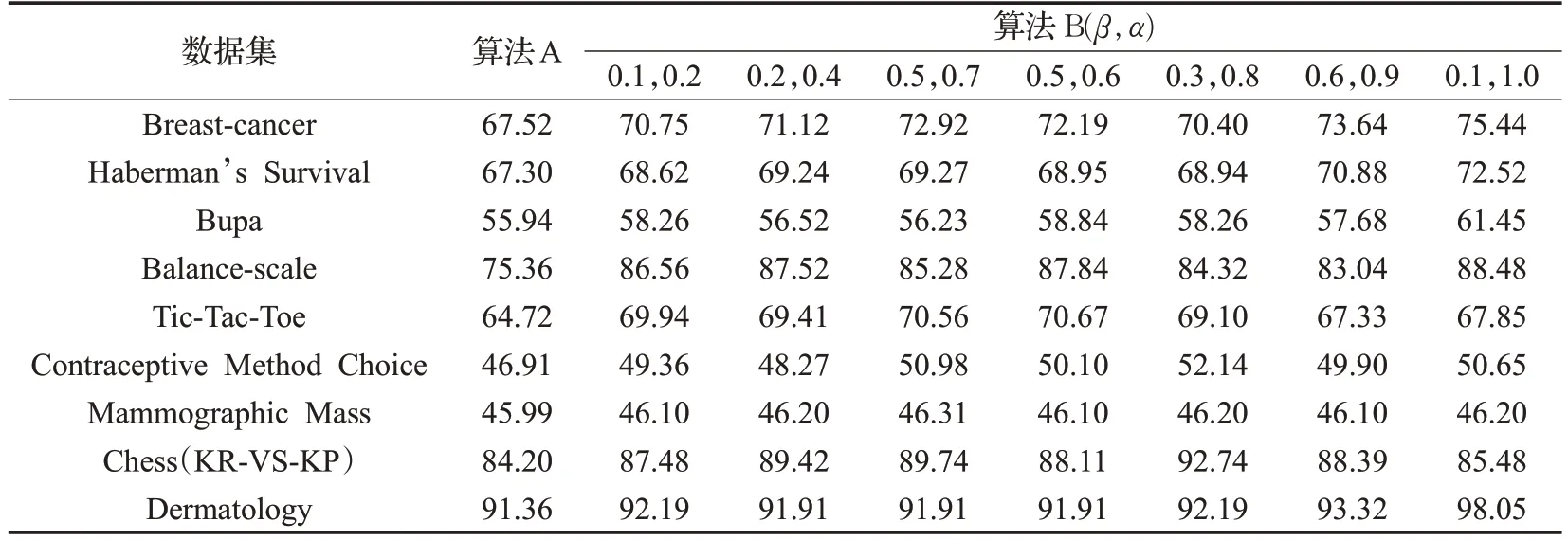
表2 分類準確率對比 %

圖10 Breast-cancer類別1-2的召回率

圖11 Haberman's Survival類別1-2的召回率

圖12 Balance-scale類別1-3的召回率

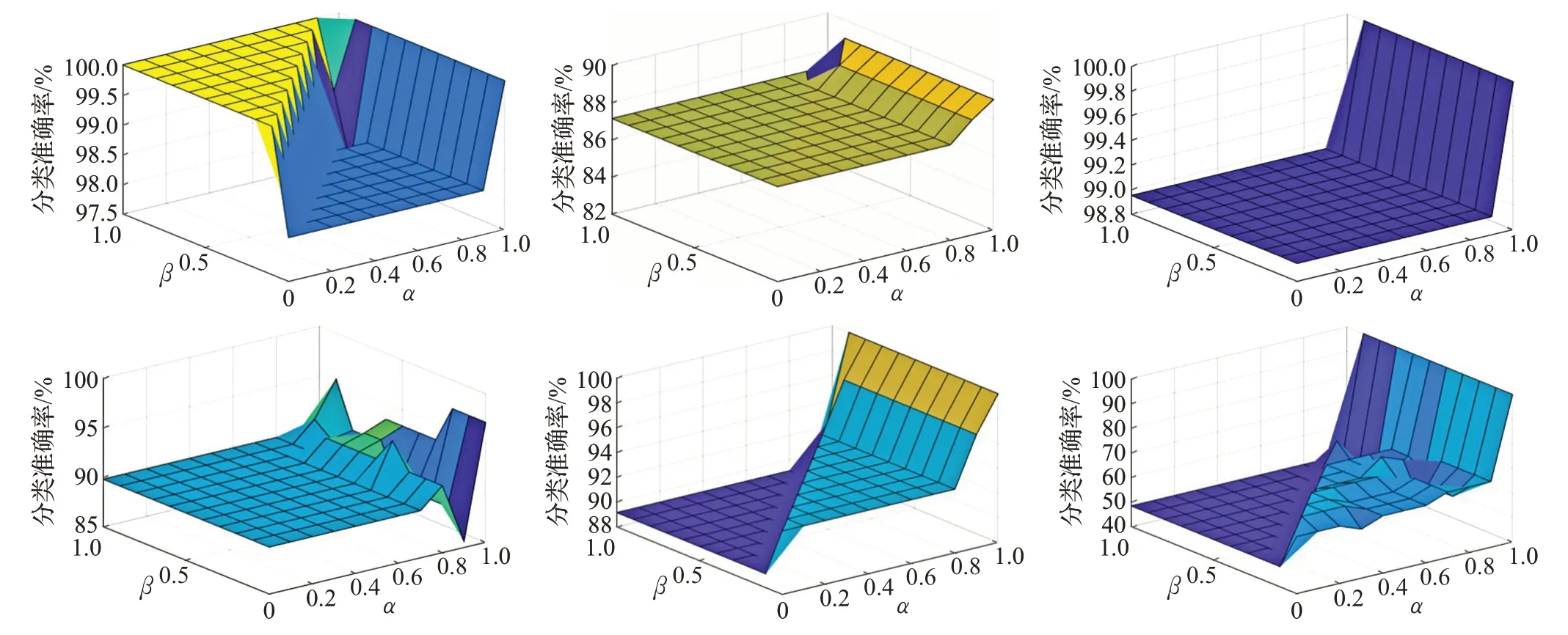
圖13 Dermatology類別1-6的召回率

表3 是算法A 與算法B 基于不同的數(shù)據(jù)集和不同α、β取值的召回率對比結(jié)果，其中，對于數(shù)據(jù)集Breastcancer，閾值α、β分別取0.7和0.5；對于數(shù)據(jù)集Haberman's Survival，閾值α、β分別取0.5和0.1；對于數(shù)據(jù)集Balancescale，閾值α、β分別取0.4和0；對于數(shù)據(jù)集Dermatology，閾值α、β分別取1和0.6。結(jié)果顯示，在α、β值選擇合適時，相較于算法A，算法B的分類召回率也有明顯的提高。

5 結(jié)束語

本文將三支決策理論融入一般樸素貝葉斯增量算法中，基于二者優(yōu)勢構(gòu)建了一種基于三支決策的樸素貝葉斯增量學習算法。首先，利用最大后驗概率和次最大后驗概率定義了一個稱為分類確信度的概念，用以度量分類的準確程度，然后結(jié)合代價函數(shù)，給出了確定三支決策理論中正域、負域和邊界域的規(guī)則；其次，利用樸素貝葉斯學習理論本身具有的增量學習特性，通過將三支決策正、負域中的錯分樣本和邊界域中的樣本作為增量數(shù)據(jù)，以增量方式更新模型參數(shù)，在提升算法性能的同時，使算法具有了代價敏感性。

表3 召回率對比 %

最后，利用UCI數(shù)據(jù)庫中的9個數(shù)據(jù)集對所提算法進行了實驗，并與文獻[1]提出的一種增量貝葉斯分類模型進行了實驗對比。實驗結(jié)果顯示，本文提出的基于三支決策的樸素貝葉斯增量學習算法可行且有效。不過，針對實際問題，基于三支決策理論的正區(qū)域、負區(qū)域和邊界域的更有效確定方法、增量學習的更有效機制，以及增量學習算法性能的進一步提升將是下一步需要探究的問題。