黏土中考慮土體卸荷效應的后注漿壓密模型

吳 悅，趙春風，王有寶，費 逸

(1.巖土與地下工程教育部重點實驗室(同濟大學)，上海 200092；2.同濟大學 地下建筑與工程系，上海 200092)

壓密注漿是指用稠度較大的漿液注入土體，通過對周圍土體的擠壓來加固土體的方式，壓密注漿最早由Graf[1]于1969年首先提出，并對其工藝進行了詳細的描述，主要應用于沉降建筑物的抬升、樁基承載力提高、土石壩的加固和隧洞掘進時地層位移的控制等方面[2].

對于壓密注漿問題，國內外已有很多學者從試驗、理論和數值等方面展開了較為深入的研究.Brown[3]、Younis等[4]也通過室內試驗和現場試驗等研究了壓密注漿的適用性以及漿液對土體的影響；El-Kelesh等[5]通過現場試驗對樁的壓密注漿加固效果進行分析，研究了土體特性、漿液注入順序、置換比等對壓密注漿效果的影響，發現漿液注入順序對樁壓密注漿效果產生很大影響；Seo等[6]通過一系列試驗研究了4種不同花崗巖殘積土壓密注漿效果對抗拔錨索抗拔承載力的影響，并通過圓孔擴張理論對試驗結果進行對比研究，發現壓密注漿提高抗拔承載力主要通過孔擴張進行壓密土體、殘余應力作用以及對土體剪脹角的影響；Nichols等[7]通過室內模型試驗得出壓密注漿漿液在土體中形成的漿泡呈現圓柱形和淚珠形兩種并且將漿泡直徑與注漿管的直徑進行比值無量綱化，從而建立了其與漿液上返高度之間的關系；張忠苗等[8]通過室內模型試驗研究了黏土中壓密注漿漿液擴散機理，發現黏土注漿中存在壓濾效應并且貫穿于整個注漿過程，壓密注漿形成的漿泡大小隨著漿液水灰比的增大而減小；鄒金峰等[9]基于能量分析法和孔擴張理論研究了土體中壓密注漿的極限注漿壓力，發現球形擴孔得出的注漿壓力比柱形擴孔的注漿壓力要小得多；張忠苗[10]、鄒健等[11]采用球形和柱形孔擴張理論對黏土中壓密注漿進行了分析，引入有效應力比并考慮了漿液壓濾效應對壓密注漿的影響，計算結果發現要比未考慮漿液壓濾效應更準確；葉飛等[12]利用球孔擴張理論，通過對壓密注漿漿液擴散擴張過程的力學分析，建立了盾構壁后壓密注漿的力學模型，分析了漿體擴張對管片襯砌產生壓力效應的影響因素主要是注漿壓力、土體彈性模量、黏聚力和內摩擦角；曾勝等[13]利用球形擴孔過程中的能量和體變守恒原理推導出壓密注漿極限注漿壓力求解的理論方程組并得出了壓密注漿的極限注漿壓力；Ivanetich等[14]通過數值方法研究了漿液特性對漿泡形成的影響；Wang等[15]通過有限元數值分析方法研究了壓密注漿漿體徑向擴張和對地表土體隆起的影響，并通過與現場試驗和理論解析結果進行對比驗證了結果的合理性，發現壓密注漿效果受控于漿體上方圓錐體重量和土的剪切強度.

現有的研究很少涉及壓密注漿在土體中存在卸荷情況條件下對土體以及結構物等力學特性影響研究，而在實際工程中經常會涉及土體中存在卸荷工況條件下注漿的情況，比如隧道拱頂注漿(襯砌背后注漿)的加固過程[12]等.為此，采用理論分析的方法，基于球孔擴張理論，在假定后注漿為壓密注漿模式下呈球形擴散方式的基礎上，通過土體彈性模量折減值來考慮不同卸荷程度對土體壓密注漿效應的影響，分析得出不同卸荷程度下壓密注漿極限注漿壓力、漿體擴張率、塑性區擴張率、徑向和環向應力沿徑向分布以及徑向位移沿徑向的分布關系，得出考慮土體卸荷效應影響的壓密注漿模型，為實際工程中壓密注漿實踐提供一定的理論指導.

1 壓密注漿模型

1.1 基本假定

為便于研究，結合已有有關壓密注漿的研究[12]，對黏土中壓密注漿球孔擴散做如下假定：

1)忽略漿液在土體交界面處的滲透效應，認為注漿過程中僅存在漿液對土體的壓密效應；

2)忽略漿液沿結構物表面的擴散運動，注漿體在土體中呈球形擴散，壓密注漿過程相當于在土體中擴張一個半徑為Ru的球形漿體，如圖1所示，p為注漿壓力，R0為球形漿體的初始半徑，Rp為土體塑性區最大半徑；

3)土體在初始狀態下為均質各向同性體；

4)土體在受到漿體擴張擠壓后發生彈塑性變形，且變形在應力施加后立刻發生；

5)漿液和土顆粒不可壓縮；

6)忽略重力對土體壓縮的影響.

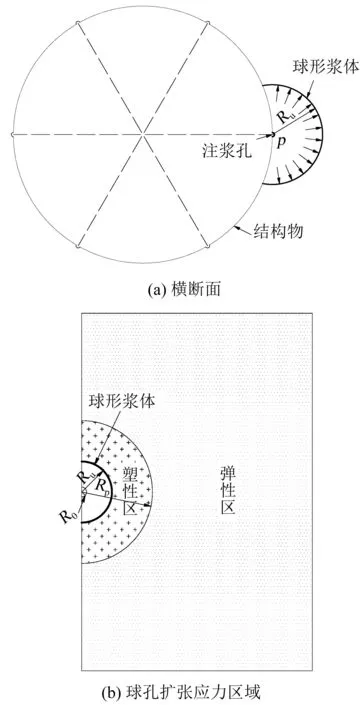
圖1 壓密注漿模型

1.2 理論推導

根據球對稱問題的平衡微分方程為

(1)

式中σr和σθ分別表示徑向和切向正應力.

幾何方程為

(2)

式中：ur為土體的徑向位移，εr和εθ分別表示徑向應變和切向應變.

物理方程為

(3)

式中υ和E分別表示泊松比和土體彈性模量.

應力邊界條件為

σr|r=Ru=p,σr|r→∞=p0.

(4)

式中：p和p0分別表示注漿壓力和初始靜壓力，Ru為漿體半徑.

當注漿壓力較小時，漿體周圍土體全部處于彈性狀態，根據彈性理論，聯立式(1)～(3)并考慮邊界條件式(4)可得彈性區應力場和位移場為

(5)

1.3 彈塑性應力分析

隨著注漿壓力的持續增大，注漿體邊緣土體逐漸進入塑性屈服狀態.塑性變形階段采用Mohr-Coulomb準則，其屈服函數表達式為

F=(σr-σθ)-(σr+σθ)sinφ-2ccosφ=0.

(6)

式中c和φ分別為土體的黏聚力和內摩擦角.將式(6)簡化為如下形式：

σr-ασθ=Y.

(7)

其中

(8)

當p=py時，漿體邊緣土體首先出現屈服，根據屈服準則式(6)和式(5)得土體進入塑性狀態的臨界壓力為

(9)

隨著注漿壓力p的進一步增大，當p>py時，在孔壁周圍土體內會形成一個半徑為Rp的塑性區，塑性區外為彈性區，彈性區和塑性區的交界面為Sc，交界面Sc上的土體徑向正應力為py.分別用Rp和py代替式(5)中的Ru和p，可得彈性區域De={r|r≥Rp,p>py}的應力場和位移場為

(10)

聯立式(1)和(6)得塑性區(Ru

(11)

式中A為待定常數.

利用塑性區應力邊界條件σr|r=Ru=p，σr|r=Rp=py，可得積分常數A為

(12)

則塑性區徑向、環向應力為

(13)

由式(12)可得塑性區外半徑Rp與當前注漿體半徑Ru和注漿壓力p之間的關系為

(14)

1.4 彈塑性位移分析

將r=Rp代入式(10)可得彈塑性邊界位移為

(15)

在孔內壁作用均勻分布壓力p(p>p0)時，孔周圍土體產生的彈塑性體積變化應該等于孔的體積變化[17]，假定某一離小孔中心初始距離為r0的點，在進入塑性區后，離小孔中心的距離變為r，即

(16)

式中：χ定義為考慮結構物表面曲率變化對漿液球形擴散的影響系數，χ的取值為(0，1]，當土體中不存在結構物表面影響時，漿液呈完整球形擴散，χ取為1，當存在結構物表面曲率影響時，χ取值范圍為(0,1)，χ具體取值對后續球孔擴張應力位移分析無影響；Δ為塑性區的體積變形.相關研究認為[16-17]，Δ受剪脹等因素的影響，可以忽略.在彈塑性邊界，有

(17)

(18)

則漿體擴張率為

(19)

塑性區擴張率為

(20)

對于塑性區位移的求解，設小孔周圍土體某一離小孔中心初始距離為r0的點，在進入塑性區后，離小孔中心的距離變為r，若令該點的位移為ur，則有

ur=r-r0.

(21)

對上式進行變換，有

r0=r-ur.

(22)

如前文所述，若塑性區的體積變形可忽略，則有

(23)

聯立式(22)和(23)有

(24)

1.5 極限注漿壓力

聯立式(14)和(18)可得注漿壓力表達式為

(25)

對于初始孔徑R0不為0，擴孔后注漿體半徑Ru→∞，則極限注漿壓力為

(26)

1.6 孔周土體彈塑性應力場和位移場

根據上述分析，可得到小孔周圍土體彈塑性狀態下的應力場和位移場的解析解如下：

(27)

(28)

(29)

2 土體卸荷效應影響

在實際工程注漿過程中，存在土體卸荷效應的影響，如隧道拱頂注漿(襯砌背后注漿)的加固過程[12]，即會產生應力釋放.在土體應力釋放過程中，土體彈性模量減小，因此，在考慮隧道拱頂注漿(襯砌背后注漿)加固過程存在的卸荷效應時，上文推導的理論公式中，彈性模量應是土體原始彈性模量的折減值.根據文獻[18]給出的對軟黏土初始彈性模量的估算公式：

Ei=C0ηsu.

(30)

式中：su為不排水抗剪強度；C0和η為無量綱系數，可根據土體的超固結比ROC和塑性指數Ip查圖2得到.

超固結比ROC的計算式為

(31)

式中:Pc為先期固結壓力，Pul為當前壓力.在考慮卸荷效應時，若引入卸荷比[19]

(32)

則式(30)可轉化為

(33)

聯立式(30)～(33)即可得出不同卸荷程度下的土體初始彈性模量折減值.

圖2 估計初始切線模量方法[18]

3 參數確定與模型適用性的討論

3.1 參數確定

從模型的推導過程可以看出，與壓密注漿漿體擴散過程有關的參數有：初始靜壓力p0、注漿壓力p、球形漿體初始半徑R0、黏聚力c、內摩擦角φ、泊松比ν.漿體初始半徑R0應與注漿孔半徑相等，注漿壓力p可通過注漿泵上的壓力表測得，土體的特性參數可通過試驗得到.

3.2 模型適用性

本文模型適用于滲透系數較小的軟黏土地層中，以及存在卸荷情況下軟黏土中進行壓密注漿，不適用于滲透系數較大的砂性土地層.本文模型未考慮漿液特性對壓密注漿效果的影響.

4 實例分析

4.1 不同卸荷程度下球形漿體和土體塑性區擴張率

按照給定的卸荷比換算出超固結比ROC帶入式(30)～(33)計算出折減后土體彈性模量值，并將上述土體參數代入式(19)和(20)，得出圖3不同卸荷程度下球形漿體和土體塑性區擴張率隨注漿壓力的變化曲線.可以看出，注漿壓力對球形漿體擴張率和土體塑性區擴張率的影響明顯.漿體擴張率和土體塑性區擴張率在初始階段均隨注漿壓力的增大而增大，并且增大的速率隨注漿壓力的增大不斷提高.當注漿壓力超過一定值后，漿體和土體塑性區擴張率趨于無窮大，此時注漿壓力值即可做為壓密注漿的極限注漿壓力.不同卸荷工況下的極限注漿壓力如表1所示.

圖3 不同卸荷比下漿體擴張率和土體塑性區擴張率與注漿壓力關系

表1 不同卸荷比下極限注漿壓力

分析表1可知，達到壓密注漿的極限注漿壓力隨著卸荷程度的增大而減小，且這種減小隨卸荷程度的改變呈非線性，當卸荷比小于0.7時，壓密注漿極限注漿壓力隨卸荷比的減小改變不明顯，當卸荷比大于0.7時，壓密注漿極限注漿壓力明顯減小，并且減小幅度隨著卸荷程度的增大而快速增長.因此，在實際注漿過程中，當土體中存在卸荷效應，要達到壓密注漿效果所需的注漿壓力時，需考慮此時土體卸荷程度的大小進而分析采用合適的注漿壓力.

4.2 不同卸荷程度下塑性區半徑與漿體擴散半徑關系

圖4給出了不同卸荷程度下塑性區半徑與漿體擴散半徑關系曲線，可以看出，塑性區半徑隨著漿體擴散半徑的增大而增大，增大速率逐漸變大并最后趨于穩定，即二者最后呈現線性增長關系.不同卸荷比條件下，塑性區半徑隨漿體擴散半徑的穩定增長速率隨卸荷比的增大而非線性減小，即卸荷程度越大，塑性區半徑隨漿體擴散半徑增長的速率越低；當卸荷比小于0.7時，土體中卸荷程度的改變對塑性區半徑隨漿體擴散半徑的增長速率影響很小；當卸荷比大于0.7時，土體中卸荷程度的改變對塑性區半徑隨漿體擴散半徑的增長速率影響較為顯著.

圖4 塑性區半徑與漿體擴散半徑關系

4.3 不同卸荷程度下徑向和環向應力沿徑向分布關系

圖5給出了注漿壓力370 kPa不同卸荷程度下注漿體周圍土體徑向和環向應力沿徑向的分布關系曲線，可以看出，同一注漿壓力下，當卸荷比小于0.8時，不同卸荷程度下注漿體周圍土體的徑向應力和環向應力沿徑向分布基本一致，當卸荷比大于0.8時，注漿體周圍同一位置處的土體徑向應力明顯高于卸荷比小于0.8時的應力.不同卸荷比條件下的環向應力均呈現沿半徑方向先增大后減小的規律，且當卸荷比小于0.8時，最小環向應力均在同一位置出現，當卸荷比大于0.8時，最小環向應力出現位置距注漿孔距離較卸荷比小于0.8情況下大.不同卸荷比條件下最小環向應力大小基本一致，約為78 kPa.徑向應力和環向應力均隨著徑向距離的增大而逐漸趨于穩定，即趨向于初始靜壓力100 kPa.

圖5 注漿壓力370 kPa不同卸荷比下土體徑向和環向應力沿徑向分布

圖6給出了同一注漿量(注漿體半徑0.5 m)不同卸荷程度下注漿體周圍土體徑向和環向應力沿徑向的分布關系曲線.可以看出，當注漿量相同時，不同卸荷程度下注漿體周圍土體徑向應力沿徑向逐漸趨于穩定，穩定徑向應力為初始靜壓力100 kPa，并且隨著卸荷程度的增大，達到穩定徑向應力的徑向距離逐漸減小；同一位置處的徑向應力隨著卸荷程度的增大而減小；對于環向應力，同樣呈現沿著徑向先減小后增大最后趨于穩定即初始靜壓力值100 kPa；達到最小環向應力值以及穩定環向應力的徑向距離隨著卸荷程度的增大而減小，并且不同卸荷程度下最小環向應力值相等，即最小環向應力值不隨卸荷程度的改變而變化.

根據環向應力計算公式(28)可知，最小環向應力出現在r=Rp情況下，即彈塑性界面處.在彈性區一側，由于柱孔擴孔使環向應力逐漸減小，在彈塑性界面處環向應力達到最小；對于塑性區一側，所有土體都滿足屈服準則，環向應力和徑向應力呈正比，隨徑向應力的變化而變化，因此，也在彈塑性界面處最小[17].此時最小環向應力為

(34)

從該最小環向應力表達式可以看出，最小環向應力σθ只與土體初始靜壓力p0和土體進入塑性狀態的臨界壓力py有關，與卸荷程度大小無關.因此，最小環向應力值不隨卸荷程度的改變而變化.

圖6 同一注漿量不同卸荷比下土體徑向和環向應力沿徑向分布

4.4 不同卸荷程度下徑向位移沿徑向分布關系

圖7給出了注漿壓力370 kPa不同卸荷程度下徑向位移沿徑向的分布關系曲線，可以看出，同一注漿壓力下注漿體周圍不同卸荷程度下土體徑向位移沿著半徑方向逐漸趨于穩定值0；當卸荷比小于0.8時，徑向位移沿半徑方向分布基本一致，當卸荷比大于0.8時，徑向位移沿半徑方向分布明顯區別于卸荷比小于0.8時情況，具體表現為：在達到穩定值之前，同一位置處的土體徑向位移，卸荷比大于0.8情況下土體的徑向位移遠大于卸荷比小于0.8時的情況；卸荷比小于0.8時土體徑向位移沿半徑方向達到穩定值的位置基本一致并且小于卸荷比大于0.8時的徑向距離.

圖8給出了同一注漿量(注漿體半徑0.5 m)不同卸荷程度下徑向位移沿徑向的分布關系曲線.可以看出，同一注漿量下周圍不同卸荷程度下土體徑向位移沿著半徑方向同樣逐漸趨于穩定值0，但達到穩定值的位置要遠大于相同注漿壓力下的情況；不同卸荷程度下的土體徑向位移沿半徑方向的分布一致，即同一注漿量下的土體徑向位移沿半徑方向的分布不受卸荷程度的影響.

圖7 注漿壓力370 kPa不同卸荷比下土體徑向位移沿徑向分布

圖8 同一注漿量不同卸荷比下土體徑向位移沿徑向分布

由不同卸荷比下對應的土體彈性模量折減值可以看出，當土體卸荷比為0.8和0.9時，對應的土體彈性模量明顯小于其他卸荷比下對應的土體彈性模量，卸荷比0～0.6內的土體彈性模量折減值變化不大，而土體彈性模量越小在同一壓力下對應的變形量則相應越大.因此，在同一注漿壓力下，卸荷比大于0.8時對應的土體徑向位移沿半徑方向分布區別于卸荷比小于0.8時的情況.而在同一注漿量下，由于最終形成的球形漿體體積一致，不同土體卸荷程度下對應的土體徑向位移沿半徑方向分布區別不明顯.

4.5 不同注漿量下徑向、環向應力和徑向位移沿徑向分布關系

為了分析卸荷工況下不同注漿量對土體內部應力和位移分布的影響，圖9給出了卸荷比0.5不同注漿量下注漿體周圍土體徑向和環向應力沿徑向的分布關系曲線，可以看出，當卸荷比相同時，不同注漿量下注漿體周圍土體徑向應力沿徑向逐漸趨于穩定，穩定徑向應力為初始靜壓力100 kPa，并且隨注漿量的增大，達到穩定徑向應力的徑向距離逐漸增大；同一位置處的徑向應力隨注漿量的增大而增大；對于環向應力，同樣呈現沿著徑向先減小后增大最后趨于穩定值即初始靜壓力值100 kPa；達到最小環向應力值以及穩定環向應力的徑向距離隨注漿量的增大而增大，并且不同注漿量下最小環向應力值亦相等，即最小環向應力值不隨注漿量的改變而變化.

圖9 卸荷比0.5不同注漿量下土體徑向和環向應力沿徑向分布

圖10給出了卸荷比0.5不同注漿量下徑向位移沿徑向的分布關系曲線，可以看出，同一卸荷比不同注漿量下土體徑向位移沿著半徑方向同樣逐漸趨于穩定值0，達到穩定值的徑向距離隨注漿量的增大而增大.

圖10 卸荷比0.5不同注漿量下土體徑向位移沿徑向分布

5 結論與建議

1)當卸荷比小于0.7時，壓密注漿極限注漿壓力以及土體塑性區半徑隨漿體擴散半徑的增長速率受卸荷程度改變的影響較小，當卸荷比大于0.7時，壓密注漿極限注漿壓力以及塑性區半徑隨漿體擴散半徑的增長速率則隨卸荷程度的增大而快速減小.因此在實際工程注漿中，要實現壓密注漿效果，必須考慮實際工況下可能存在的土體卸荷工況以及卸荷程度的大小.

2)同一注漿壓力下，當卸荷比小于0.8時，注漿體周圍土體的徑向應力、環向應力以及徑向位移沿徑向分布基本一致，當卸荷比大于0.8時，注漿體周圍同一位置處的土體徑向應力以及徑向位移明顯高于卸荷比小于0.8時的情況.

3)同一注漿量下，相同位置處的徑向應力、達到最小環向應力、穩定環向應力和徑向應力的徑向距離均隨著卸荷程度的增大而減小，但是土體徑向位移分布不受卸荷程度的影響；最小環向應力大小不受卸荷程度的影響但出現位置受其影響.

4)同一卸荷比下，相同位置處的徑向應力、達到最小環向應力、穩定環向應力、穩定徑向應力以及穩定徑向位移對應的徑向距離均隨著注漿量的增大而增大，但最小環向應力值不隨注漿量的改變而變化.