SINS輔助的星敏感器在線標定方法
谷 叢, 劉 洋, 吳成智, 肖 波, 林建華
(1.上海航天控制技術(shù)研究所,上海201109;2.上海慣性工程技術(shù)研究中心,上海201109)
0 引言
航天器姿態(tài)信息對于航天飛行任務至關(guān)重要,單純地依靠某一種導航方式已不能滿足航天器對姿態(tài)精度的要求。因此,通常采用將多種導航設備進行最優(yōu)組合的方式來提高導航系統(tǒng)的精度[1]。由于捷聯(lián)慣導系統(tǒng)(Strapdown Inertial Navigation System,SINS)與星敏感器均具有不向外輻射任何信息、抗干擾性強、隱蔽性好、完全自主等特點,SINS/星敏感器組合導航系統(tǒng)必將成為現(xiàn)代軍事及民用領(lǐng)域內(nèi)的一種重要導航系統(tǒng)。可以充分利用星敏感器的長期高精度定姿信息和SINS的短期高精度導航信息,通過Kalman濾波技術(shù)將它們有機結(jié)合起來構(gòu)成組合導航系統(tǒng),從而達到取長補短的目的[2-3]。但是在實際飛行任務中,星敏感器會受到發(fā)射時的振動和沖擊、惡劣的太空工作環(huán)境等因素影響,其內(nèi)部參數(shù)會相對于地面標定時發(fā)生較大變化,這將嚴重影響星敏感器的定姿精度。因此,必須對星敏感器的安裝誤差進行嚴格的在軌實時標定,其安裝誤差的實時標定與修正是確保星敏感器測量精度的關(guān)鍵[4-5]。
國外學者最先開始了對星敏感器在線標定技術(shù)的研究:Shuster等[6]研究了姿態(tài)敏感器相對和絕對準線安裝誤差的在軌標定;Crassidis等[7]研究了包括擴展Kalman濾波算法的三軸磁強計實時在軌標定方法;Pittelkau[8]提出了對準Kalman濾波算法用于陀螺和星敏感器的在軌標定,但模型復雜,計算量大。近年來,國內(nèi)學者在姿態(tài)敏感器在軌標定方面也取得了較多研究成果[9-10],但星敏感器在軌標定方法在算法實時性、模型效率和最優(yōu)性以及誤差源考慮等方面還值得進一步深入研究。為此,本文提出了一種SINS輔助的星敏感器在線標定方法。該方法不需要采用造價昂貴的高精度轉(zhuǎn)臺和模擬星光學設備等,只需飛行器在飛行過程中做簡單的搖翼動作,即可對星敏感器的安裝誤差角進行實時在線標定,工程應用價值高。
1 星敏感器姿態(tài)輸出
星敏感器測量坐標系c與載體坐標系b之間的姿態(tài)轉(zhuǎn)換關(guān)系在星敏感器安裝時可以確定。為方便起見,這里假設星敏感器測量坐標系c與載體坐標系b基本重合,僅存在殘余安裝誤差角α=[αxαyαz]T(小角度), 如圖1所示, 則有

式(1)中,(α ×)為由α構(gòu)成的反對稱陣, 即。
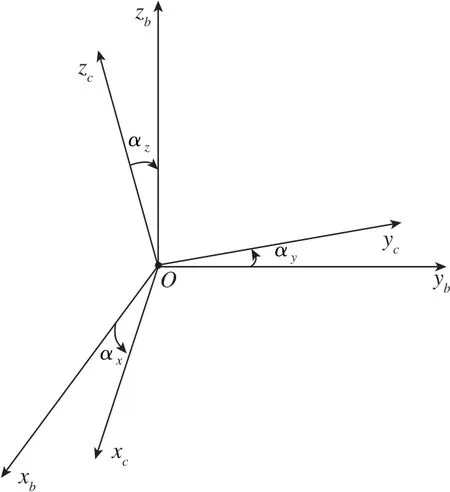
圖1 星敏感器坐標系與載體坐標系安裝誤差示意圖Fig.1 Installation error diagram of star sensor and carrier coordinate system
由于星敏感器的測量精度很高,標定星敏感器的安裝誤差以后,星敏感器自身的測量誤差vcns可以認為是零均值的白噪聲。所以,實際星敏感器相對于慣性坐標系的輸出為
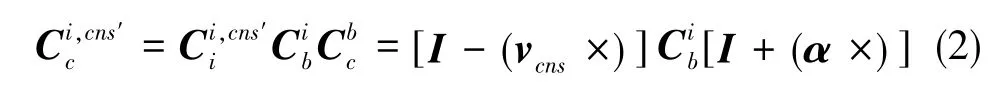
2 SINS姿態(tài)輸出

式(3)中,np和nc分別為由計算姿態(tài)和計算位置確定的導航坐標系,設真實位置處的導航坐標系為nt, 則式(3)可展開為

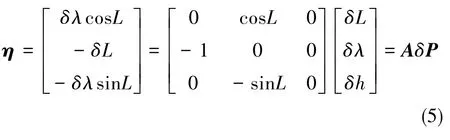
代入式(4),忽略高階小項,整理可得
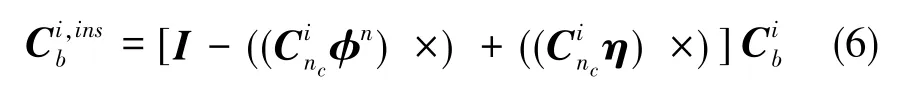
3 SINS/星敏感器組合導航狀態(tài)方程
針對SINS系統(tǒng),假設慣性器件的其他誤差項已得到很好的校正,只考慮其姿態(tài)誤差φn、速度誤差δvn、位置誤差δpn、陀螺隨機常值漂移εb以及加速度計隨機常值誤差Δb。對于星敏感器,僅考慮其安裝誤差角α。 因此,SINS/星敏感器組合導航系統(tǒng)的狀態(tài)向量x為狀態(tài)方程為

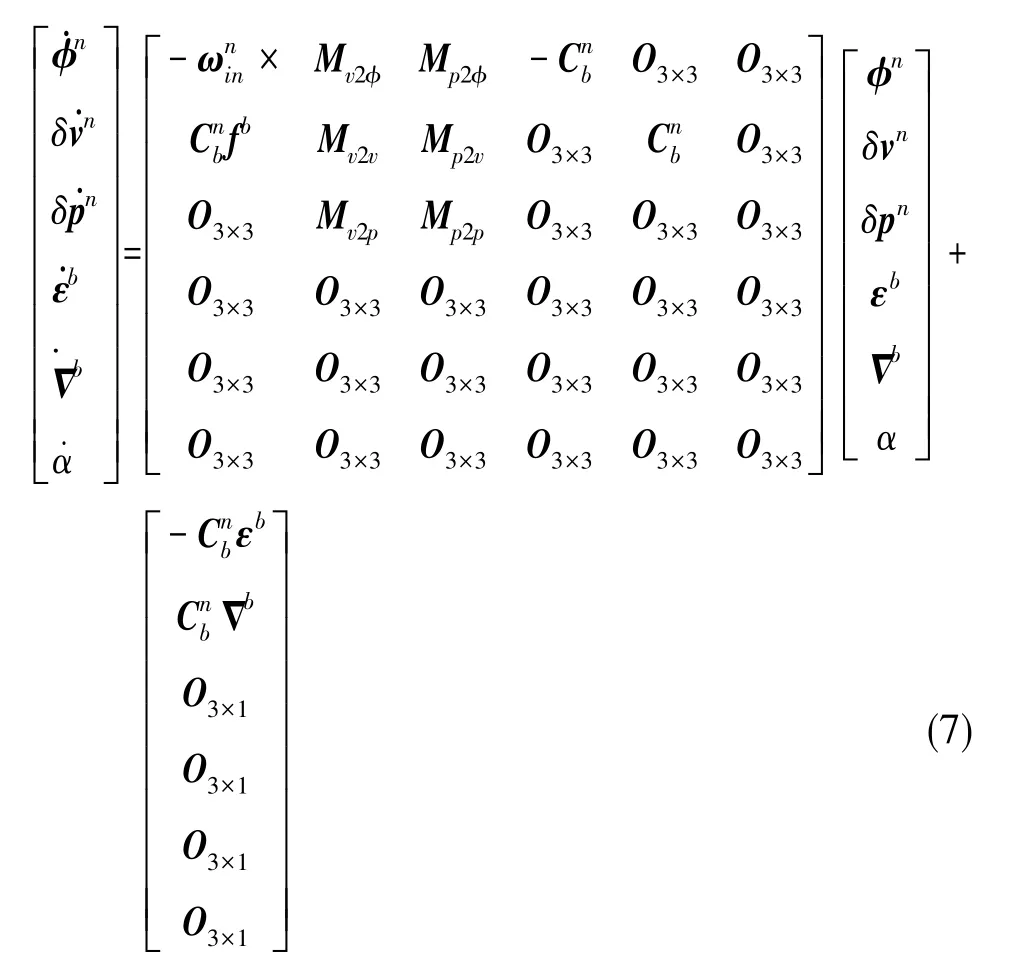
式(7)中,ω為陀螺輸出的角度信息,f為加速度計輸出的比力信息,其余相關(guān)矩陣分別為

式(8)中,RMh為子午圈曲率半徑,RNh為卯酉圈曲率半徑。
4 SINS/星敏感器組合導航系統(tǒng)量測方程

根據(jù)叉乘反對稱矩陣特性,從式(9)中提取量測量

可得量測方程為
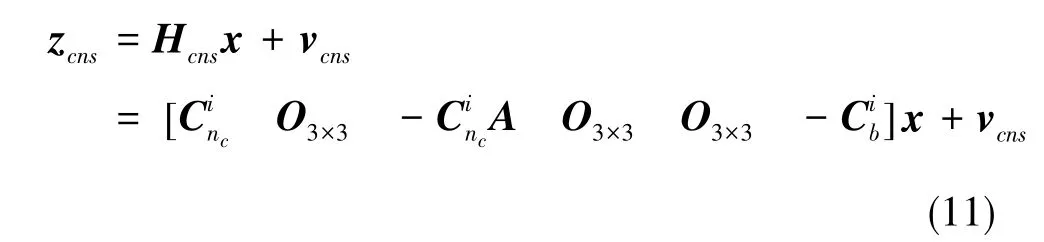
當飛行器角運動使星敏感器安裝誤差角充分可觀測后,極限估計精度與星敏感器的精度相當。
5 仿真驗證
5.1 慣性器件參數(shù)設置
試驗系統(tǒng)采用光纖捷聯(lián)慣導,陀螺常值漂移為 0.05(°)/h, 角隨機游走系數(shù)為 0.008(°)/h1/2,刻度系數(shù)誤差為1×10-4;加速度計常值偏置為4×10-5g,速度隨機游走為1×10-5g·s1/2,刻度系數(shù)誤差為1×10-4。 設慣導姿態(tài)初始誤差為[30′ 30′30′]T,星敏感器和慣導間的安裝誤差角為[10′ 20′ 30′]T,星敏感器精度如表1所示。

表1 星敏感器精度Table 1 Accuracy of star sensor
5.2 飛行器軌道設置
將飛行器軌道高度h設置為400km,地球半徑Re=6378160m,得軌道半徑R為

飛行器的飛行速度v、角速率ωr、向心加速度ac分別為

設軌道的升交點赤經(jīng)Ω=20°,軌道傾角φ=40°。
設軌道的初始角位置θ0=60°, 即初始位置為

5.3 飛行器機動結(jié)果
(1)機動角速率的影響
設飛行器從10s開始機動,先繞橫滾軸角機動80s,往復搖翼一次,休息60s,再繞航向軸角機動80s,此后繞軌道勻速飛行。根據(jù)表1,設角速率分別為 0.1(°)/s、 0.6(°)/s、 1(°)/s 三個等級,易知三個等級中的搖翼幅度分別為2°、12°和20°。慣導姿態(tài)角和星敏感器與慣導間的安裝誤差角曲線分別如圖2和圖3所示。

圖2 不同角速率下慣導姿態(tài)角Fig.2 Attitude angles of SINS under different angular velocities
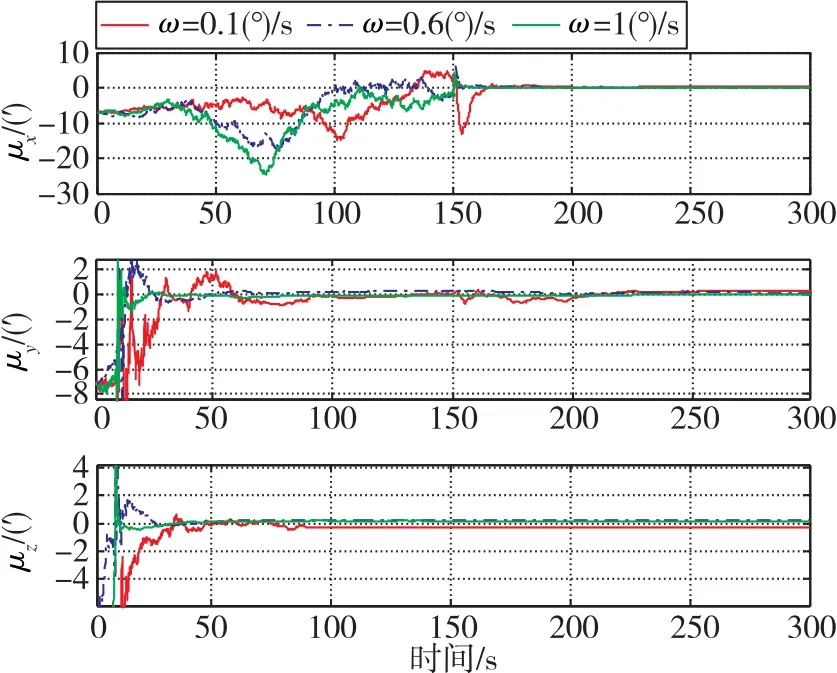
圖3 不同角速率下星敏感器與慣導間的安裝誤差角Fig.3 Installation error angles between SINS and star sensor under different angular velocities
由圖2和圖3可知,飛行器10s開始繞橫滾軸x機動時,俯仰軸y和航向軸z的星敏感器與慣導間的安裝角迅速得到估計;150s后繞航向軸z進行角機動后,方能估計出橫滾軸x的安裝誤差角。相同機動時間,角速率越大,即搖翼幅度越大,慣導姿態(tài)角和星敏感器與慣導間的安裝誤差角收斂速度越快。仿真結(jié)束時刻,星敏感器與慣導間的安裝誤差角約為 0.1′(角速率為 0.6(°)/s 和 1(°)/s)和 0.4′(角速率為0.1(°)/s),即搖翼幅值越大,收斂精度越高,安裝誤差的總體估計率達到95%以上。
(2)機動時間的影響
飛行器從10s開始以0.6(°)/s的角速率繞橫滾軸x往復搖翼一次,完成一次搖翼的時間分別為80s、 160s、 240s, 即搖翼幅度分別為 12°、 24°和48°三個等級。慣導姿態(tài)角和星敏感器與慣導間的安裝誤差角曲線分別如圖4和圖5所示。
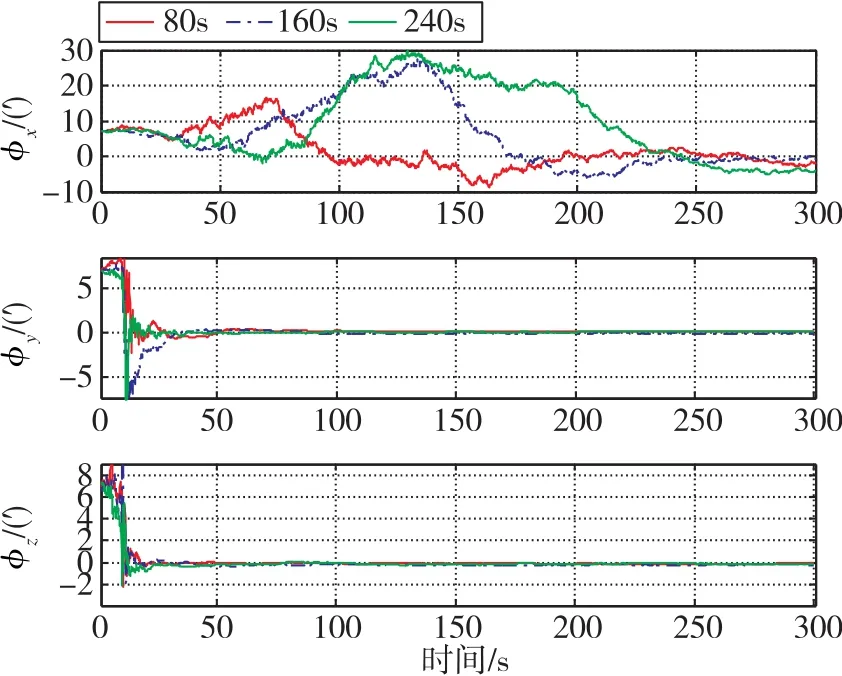
圖4 不同搖翼時間下的慣導姿態(tài)角Fig.4 Attitude angles of SINS under different wing times

圖5 不同搖翼時間下的星敏感器與慣導間的安裝誤差角Fig.5 Installation error angles between SINS and star sensor under different wing times
由圖4和圖5可知,飛行器10s開始繞橫滾軸x機動時,x軸的星敏感器與慣導間的安裝角無法得到估計;進一步驗證了若估計出三個軸向的星敏感器安裝誤差角,飛行器必須進行至少兩個軸向的角機動。飛行器以相同角速率進行機動時,機動時間越長,幅值越大,慣導姿態(tài)角和星敏感器與慣導間的安裝誤差角收斂速度越快,精度越高。
6 結(jié)論
本文研究了航天器在飛行過程中如何利用SINS對星敏感器和慣導間的安裝誤差角進行標定的方法。將SINS/星敏感器輸出的姿態(tài)信息進行配準,構(gòu)建了SINS/星敏感器組合導航系統(tǒng)的Kalman濾波模型,并對算法進行了數(shù)學仿真。利用本文提供的在線標定方法,飛行器在進行兩個軸向的角機動后,星敏感器和慣導間的安裝誤差角可迅速得到估計,收斂速度和估計精度與飛行器機動幅值相關(guān)。針對不同角速率對應的星敏感器精度不同,應選擇合適的角速率盡量延長機動時間,快速精確估計出星敏感器的安裝誤差角。本方法有效保證了星敏感器的定姿精度,具有良好的理論研究與工程應用價值。

