利用改進DBSCAN聚類實現多步式網絡入侵類別檢測

羅文華，許彩滇

(中國刑事警察學院 網絡犯罪偵查系， 沈陽 110035)E-mail:luowenhua770404@126.com

1 引 言

隨著存儲空間及計算能力的迅速進步，對搜集、存儲、管理及處理數據的能力大幅度提升，在網絡入侵檢測中應用機器學習技術，已成為近年來安全領域的研究熱點[1].常用于網絡入侵檢測的算法有Kmeans、DBSCAN、PCA、K-NN、SVM、貝葉斯分類等算法.但這些算法的檢測率較低或者誤檢率高，通過進一步改進提高了檢測能力[2].Wei-Chao Lin等[3]將Kmeans算法和Knn算法結合使用后形成新的入侵檢測算法CANN，并基于KDDCUP 99數據集對該算法進行了較有效的驗證.戴敏[4]構建一種并行化的量子粒子群優化(QPSO)算法，對KDDCUP 99數據集進行特征選擇，實現一種并行化的樸素貝葉斯分類器用于網絡入侵檢測.郭慧等[5]通過云模型對KDDCUP 99數據集連續屬性進行離散化，引入加權選擇概率函數，使得決策樹算法能檢測出全部類別攻擊.然而，上述網絡入侵檢測算法多為單步式檢測的形式，具有一定的缺點.

單步式網絡入侵檢測算法在檢測非平衡(各類數據分布嚴重不均)數據集時，往往難以準確高效地檢測所有類別的數據.例如，對于罕見攻擊U2R類數據，由于其占比很低，被檢測的成功率往往不高[6].Solane Duque等[7]利用基于簽名的K-means算法構建一個自動識別數據類群的入侵檢測算法，一次性對NSL-KDD數據集劃分，雖降低了誤報率，但整體類別的數據的檢測率較低.相比單步式檢測，多步式檢測通過逐步劃分減少數據量的方式將非平衡數據往均衡狀態方向發展，提升罕見入侵行為數據的被檢測率.不僅能適應平衡數據集，也能良好地適應非平衡據集，具有更強的應用性.因此，考慮將基于聚類算法的多步檢測思路應用到網絡入侵類別檢測中.

K-means算法作為一種常用的入侵檢測聚類算法，其應用廣泛、實現簡單.但是，K-means聚類算法的初始聚類中心是隨機選取的，聚類中心數需要人為設定，導致聚類結果不穩定[8]；并且K-means聚類算法基于距離劃分數據，結果簇趨向于球形[9]，對非球形分布數據的適用性較差.DBSCAN聚類算法則是一種基于密度劃分數據的方法，不需要事先設定聚類中心的數量[10].由于基于密度劃分，DBSCAN算法能夠根據數據在空間分布的密度情況自行劃分簇數，而且數據密度分布是穩定的，使得聚類結果具有穩定性.但是，DBSCAN算法需要人為設定最小包含點數(MinPts)和掃描半徑(Eps)參數，依賴多次經驗才能合理地選擇參數，否則難有準確的聚類結果.為使入侵檢測輸出準確穩定的聚類結果，提升檢測方法對球形與非球形數據的適用性，提出一種基于密度自適應計算參數的改進DBSCAN聚類算法.

基于多步檢測思路及改進DBSCAN聚類算法，提出一種基于改進DBSCAN聚類的多步式網絡入侵類別檢測算法.該算法可以實現網絡行為數據的自動聚類以及優化，并對于如何依據數據自身分布確定DBSCAN聚類參數進行了深入研究.本文按如下結構進行組織，除“引言”部分外，第2節著重于描述NSL-KDD數據集以及對其數據的特征處理過程；第3節重點基于入侵檢測視角說明如何對DBSCAN聚類算法進行改進，闡述自適應計算聚類參數的方法與依據；第4節說明基于改進DBSCAN聚類的多步式網絡入侵類別檢測過程；第5節展示入侵檢測效果，并與其他入侵檢測方法進行比較說明；第6節對本文的主要工作進行總結，指出了不足并說明未來研究的方向.

2 數據集確定及特征處理

NSL-KDD訓練集[11]有125973條數據，測試集有22544條數據.這些數據有42維，其中前41維為特征值，第42維為屬性標識.NSL-KDD數據集包含Normal、Dos、Probe、U2R和R2L五大類行為數據，且各類數據的占比類似于現實中各類行為出現的頻率，故NSL-KDD數據集適合作為入侵類別檢測算法的驗證數據集.隨著NSL-KDD數據集越來越廣泛應用于網絡入侵檢測領域，NSL-KDD數據集驗證網絡入侵檢測算法的有效性得到普遍認同，具有權威代表性.

NSL-KDD數據集可以通過提取代表性維度進行降維，提高效率并找出有用的特征子集.Sang-Hyun Choi和Hee-Su Chae[12]基于NSL-KDD數據集將一種有效的分類決策樹算法應用于評估維度約簡方法選取代表性維度.劉白璐、楊雅等[13]以遺傳算法和SOM神經網絡作為評價模型，將39維早期特征減少為29維.ZHANG Xue-qin等[14]利用Fisher評分方法對每個維度進行評分，依據維度評分的大小選取具有代表性維度.相對于分類決策樹約簡維度的方法，以及基于神經網絡選擇特征的方法，以Fisher評分作為維度評分方法，能夠在不同劃分情形下自動判斷出代表性維度，達到數據降維的目的，實現在低維度空間按照劃分順序劃分數據.同時，代表性維度可以按其Fisher評分在所有維度評分總分的占比，重新被賦予權重，使各維度在檢測過程中的權重符合其劃分能力.

2.1 轉化文字型特征值

NSL-KDD數據集中Protocol_type(2)、Service(3)、Flag(4)維度的特征值為文字型，如Tcp、ftp_data和SF,無法直接參與到Fisher評分和聚類中的樣本間距離計算.若直接排除這3個維度的特征值，可能影響到維度評分和聚類的結果.因此，保留這3個維度的特征值，并用文字型特征值在數據集中出現的次數替換對應的數值型特征值.在同一維度中，文字型特征值替換它們自身出現的次數后，能夠反映出與其他特征值的差異.轉化后，Protocol_type(2)、Service(3)、Flag(4)維度的特征值與其他維度的特征值共同參與維度評分和聚類.

2.2 基于改進Fisher評分進行維度評分

NSL-KDD數據集的每一個樣本是41維的特征向量及屬性標識，在入侵檢測需要進行降維操作，以此減少大數據量聚類需要的算力要求，實現高效準確的入侵檢測.在多維度中選取一部分具有代表性的特征維度，是一種常見有效的降維方法.Fisher評分具體實施時，在多維度中挑選一個維度的特征向量作為分類依據，利用SVM向量機分類出訓練集中的正常簇和異常簇，然后計算此維度的特征向量對應的Fisher評分，循環上述過程，直到多個維度的Fisher評分計算完成.在分類正常簇和Dos簇、正常簇和Probe簇、正常簇和U2R簇、正常簇和R2L簇時，也可以使用上述Fisher評分方法.Fisher評分的定義為：

(1)

其中，Sb為兩個簇間的距離，Sw為簇內距離.

(2)

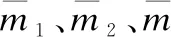
(3)

(4)

(5)

其中，x∈+1和x∈-1的+1、-1分別表示正常簇、異常簇，x表示節點特征值.而Sw的定義為：

Sw=S1+S2

(6)

(7)

(8)

其中，N1是正常簇中的節點數，N2是異常簇中的節點數；σ1、σ2分別為正常簇、異常簇內距離方差.

但是，上述方法中基于SVM向量機進行分類具有一定的缺陷.由于SVM向量機很難確保核函數完全讓數據集線性可分，這導致分離面難以準確介于兩個不同類之間.所以，為緩解這個問題，SVM向量機允許分離面處于軟間隔狀態，一些介于ε間隔帶(位于分離面兩側，寬度為ε)樣本會被分錯.

針對此缺陷，結合SVM向量機和KNN算法的SVM-KNN算法[15]，能對處于ε間隔帶的樣本進一步確定屬性.首先用SVM向量機分類數據集，然后基于KNN算法對落入ε間隔帶的樣本點重新分類，改善分類效果.將Fisher評分方法中的SVM向量機改進為SVM-KNN分類算法，提升評分的準確度.

2.3 代表性維度按比例賦予權重

由于每個維度的特征值的最大值不同，在用多維度數據計算樣本點間距離時，特征值總體偏大的維度數據對計算結果影響更大，而特征值總體偏小的維度對計算結果影響會變小，造成維度間的地位偏離Fisher評分結果.例如:計算樣本點1(100,0.01)與樣本點2(50,1)間的距離，其中維度2的Fisher評分高于維度1.可知，這種情況下，即使維度2比維度1更具有劃分能力(Fisher評分)，但由于維度1的特征值總體上大于維度2，造成距離的計算結果絕大程度上受維度1影響.

因此，在數據預處理階段增加維度按比例加減權這一步驟.讓具有代表性的維度按照各自Fisher評分占總分的比例，對其賦予相應的權重.維度按比例賦予權重的過程如下：

(9)

說明：xi為某維度中的特征值，xmax為維度中最大的特征值，Fi為維度i的Fisher評分，Fsum為各維度的Fisher評分之和，100為總權重，Xi為xi更新后的值.

3 DBSCAN聚類算法的改進

通過改進DBSCAN聚類算法，實現其能夠自動且較準確地劃分網絡行為數據.在改進DBSCAN聚類應用于多步式網絡入侵類別檢測時，該聚類算法能自動且較準確地劃分出不同網絡入侵類別的數據，實現較好的檢測效果.

3.1 改進基本思路

由于數據在多維空間中的分布體現出相似性和相異性，相似的數據相互靠得近，而相異的數據互相離得遠.所以，相似數據所在的區域呈現凝聚態，樣本點的分布密度較高，而相異數據間的區域為簇間分隔區域，樣本點分布密度較低.在高密度數據集合之間存在著低密度區域，且低密度區域存在著一定的寬度.所以，在樣本點密度參數不低于臨界點(其恰好能分辨出兩個簇間的空間，指明這個空間是簇間分隔區域)的情況下，隨著密度參數的逐漸降低，聚類結果的簇數會呈現收斂狀態，并在一定密度值區間內保持穩定.同時，密度值越小，則噪聲率越低，而且聚類結果越準確[16].這是因為隨著密度參數的降低，越多的低密度樣本點被劃分進簇，因此噪聲率變低.綜上所述，在一定密度值區間內，密度參數越小，則聚類效果越好.因此，臨界點密度是最理想的DBSCAN算法參數，其對應的樣本點數及拐點半徑即為最小包含點數(MinPts)和掃描半徑(Eps)參數.

3.2 聚類參數的計算

基于最小二乘法曲線擬合和樣本點密度分布情況，自適應計算聚類參數.實驗發現用曲線擬合計算拐點半徑的思路計算每個點到其他點的距離后，統計距離與樣本點數的關系，可以發現在某個距離區間內存在密集的點，這個密集的區域到中心點的半徑可作為DBSCAN聚類的掃描半徑(Eps)，即拐點半徑ri.

拐點半徑ri計算方法為：首先計算樣本點xi與其他樣本點xj的歐氏距離dij，將距離集{j=1,…,n(j≠i)|dij}從大到小排序,得到新的距離集{1≤m≤(n-1)|dm}；然后以距離集{1≤m≤(n-1)|dm}作“m-dm”曲線圖(橫坐標為dm對應的序號m，縱坐標為距離dm)；最后基于最小二乘法曲線擬合原理，利用三次方程擬合“m-dm”二維曲線；并利用二階求導計算出曲線拐點對應的縱坐標y值，y即為拐點半徑ri，如圖1.

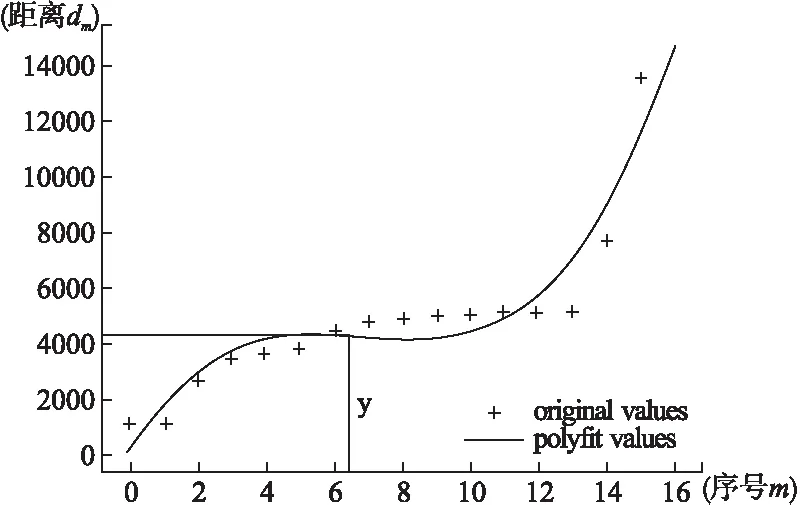
圖1 基于距離集計算拐點半徑

通過三次方程曲線擬合和二階求導，可大致計算出這個半徑ri和在此區域內的樣本點數ni.遍歷數據集，計算每個點對應的拐點半徑ri，及以ri為半徑的空間區域內的樣本點數ni，并求出相應的樣本點密度，形成密度集densitydata.

在選擇最小包含點數(MinPts)和掃描半徑(Eps)參數時，由于這兩個參數在聚類中全局使用，所以它們應該盡可能多地區分出簇間分隔區域.密度集densitydata有每個點對應的點分布密度，將其按大小順序排列，繪制分布曲線，呈現出一段密度曲線平緩穩定的區間range，見圖2.當聚類參數的密度在區間range左邊時，密度對應的參數值低于大部分樣本點周圍的密度，容易將簇間分隔區域錯誤識別為簇內區域；當聚類參數的密度在區間range右邊時，密度對應的參數值高于大部分樣本點周圍的密度，容易將簇內區域錯誤識別為簇間分隔區域.密度區間range中的最小密度值最接近于臨界點密度，其對應的拐點半徑ri及樣本點數ni作為DBSCAN聚類算法的MinPts 和 Eps 參數.

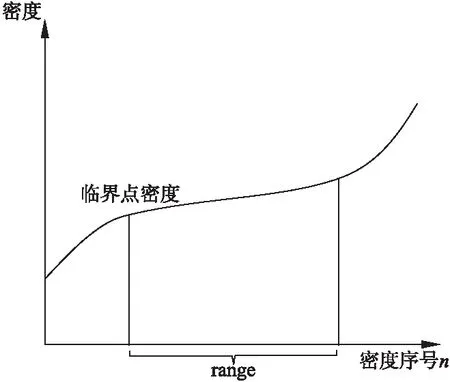
圖2 密度曲線的穩定區間range

3.3 具體聚類步驟

Step 1.計算樣本點xi與其他樣本點xj的歐氏距離，距離集{j=1,…,n(j≠i)|dij}從大到小排序,得到新的距離集{1≤m≤(n-1)|dm}；

Step 2.用新的距離集{1≤m≤(n-1)|dm}基于最小二乘法曲線擬合，產生三次方程，通過對此三次方程二階求導計算樣本點xi的拐點半徑ri及樣本點數ni，然后計算樣本點對應的密度ρ；

Step 3.循環Step 1-Step 2，遍歷數據集的每一個樣本點，計算出每個樣本點對應的密度ρ，形成密度集densitydata；

Step 4.密度集densitydata有每個樣本點的密度ρ，將其按大小順序排列，基于最小二乘法曲線擬合，產生三次方程，通過對此三次方程一階求導計算出曲線的凸點D；

Step 5.用凸點D對應的半徑和樣本點數作為DBSCAN聚類中的MinPts 和 Eps 參數；

Step 6.檢查數據集中尚未檢查過的樣本點xi，如果其未被處理(即被標為噪聲點或被劃分到某個簇)，則檢查其鄰域(掃描半徑Eps內的區域)，若包含的對象數大于或等于最小包含點數MinPts，則建立新的簇Ci，將其中所有的樣本點xi劃分到候選集N，否則將xi標記為噪點；

Step 7.對候選集N中所有尚未被處理的樣本點xi，檢查樣本點xi的鄰域，若至少包含MinPts個樣本點，則將這些樣本加入候選集N中；

Step 8.如果樣本點xi未歸入任何一個簇，則將樣本點xi劃分到Ci中；

Step 9.重復Step 7-Step 8，繼續檢查候選集N中未處理的對象，直到候選集N為空集；

Step 10.重復Step 6-Step 9，直到全部樣本都被劃分到某個簇中或被標為噪聲.

4 多步式網絡入侵類別檢測

4.1 基于Fisher評分確定多步檢測順序

采用多步檢測的目的是通過對網絡行為數據集的逐步劃分減少大類數據量，將非平衡數據往均衡狀態方向發展，并且既要保證大類網絡行為數據的檢測率，又要提升罕見入侵行為數據的檢測率.由于多步檢測順序要能夠整體上準確劃分好各類數據，故每一步劃分情形的特征維度劃分效果影響著整體的檢測結果.多步檢測順序的確定，應以網絡行為數據集的具體特征為基礎，評價特征維度在不同劃分順序的每一步劃分情形下的價值，并以此價值的總和為考量確定多步檢測順序.改進的Fisher評分是一種評價特征維度價值的方法，可應用于多步檢測順序的確定

不同的劃分順序，其Fisher評分的總體分數不同.由于維度的Fisher評分越大，其在劃分數據時的效果越好.因此，為了提高聚類算法的劃分效果，應該選擇總體上Fisher評分較高的劃分順序.

選用順序1和順序2[17]進行比較，順序1為實驗假設,結果如表1所示.

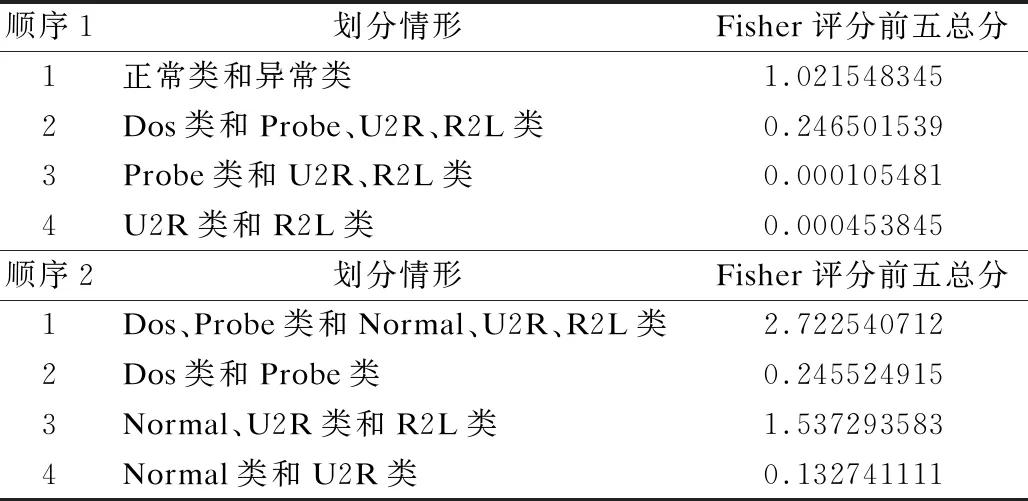
表1 不同劃分順序的Fisher評分情況

由表1可知，劃分順序2的總體Fisher評分更高，故入侵類別檢測的多步順序為：

Step 1.將NSL-KDD數據集劃分為2類，大類為Normal、U2R、R2L類，小類為Dos、Probe類；

Step 2.將Step 1中的Dos、Probe類劃分為2類，大類為Dos類，小類為Probe類；

Step 3.將Step 1中的Normal、U2R、R2L類劃分為2類，大類為Normal、U2R類，小類為R2L類；

Step 4.將Step 3中的Normal、U2R類劃分為2類，大類為Normal類，小類為U2R類.

4.2 多步式網絡入侵類別檢測流程

在確定多步檢測順序后，結合數據特征處理，基于改進DBSCAN聚類算法進行多步式網絡入侵類別檢測，具體流程見圖3.

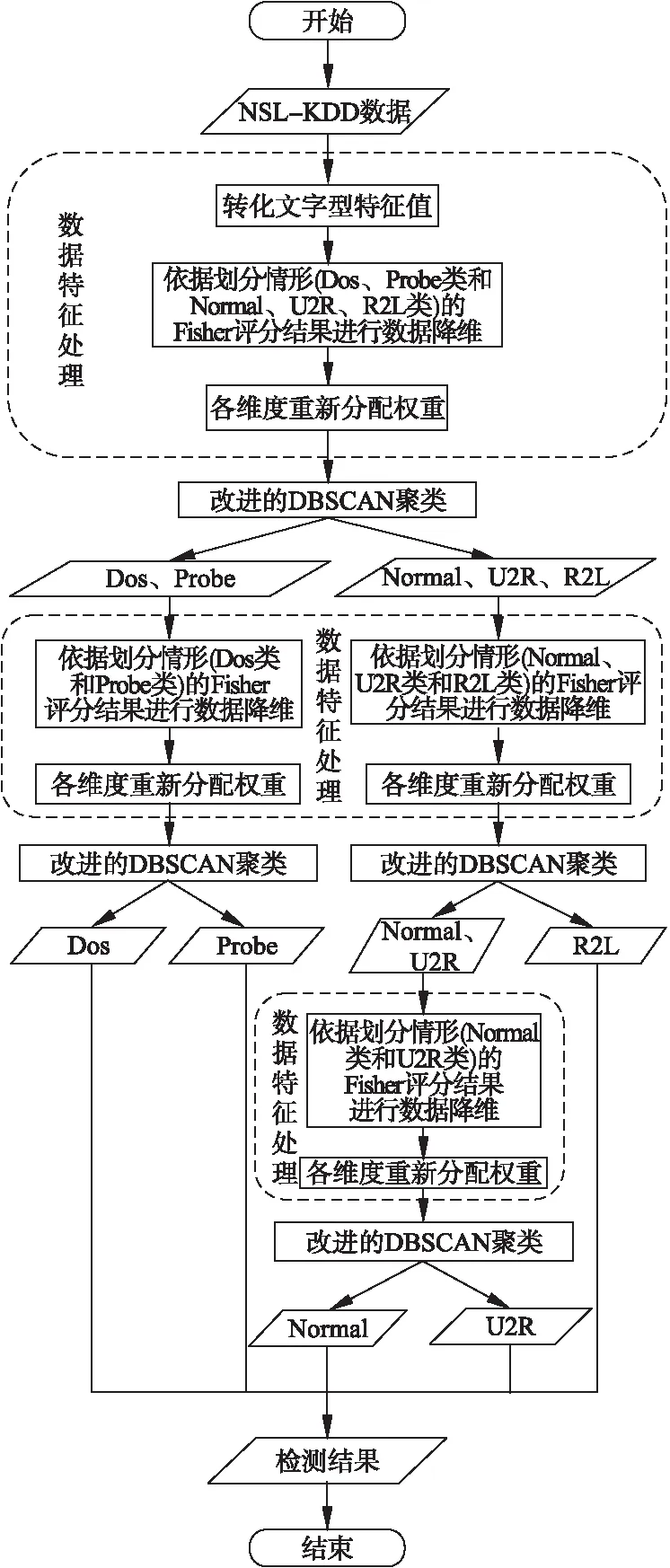
圖3 檢測流程

圖3中，1) 轉化文字型特征值：以各特征值的出現頻次替代 NSL-KDD數據的Protocol_type、Service、Flag維度的文字型特征值；2) 各維度重新分配權重：數據降維后，參與下一步聚類的維度按各自Fisher評分在總分的占比，重新被分配權重；3) Dos、Probe、Normal、U2R和R2L表示不同類別的網絡行為數據集群；4) 檢測結果：收集劃分好的各類網絡行為數據，并標識及輸出.

5 實驗結果分析

實驗平臺為64位的Windows 10系統，內存為8GB，CPU為英特爾酷睿i7-7700HQ.算法實現的過程使用編程語言Python 3.7.實驗過程見圖4.

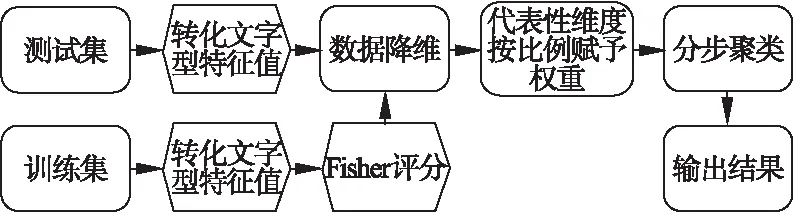
圖4 檢測的實驗過程

實驗中，訓練集的作用僅為Fisher評分，而數據降維及其后面的各階段只有測試集參與.

多步聚類按第3節確定的順序進行.在每一步聚類前，依據具體的劃分情形選取Fisher評分結果，然后對測試集進行數據降維，以及將代表性維度按比例賦予權重.更新后的測試集被輸入到聚類算法中，基于自適應設參的DBSCAN聚類算法對其進行劃分.

5.1 評估指標

將聚類的數據集按其真實類別與聚類算法預測類別的組合分為真正例(TP)、假正例(FP)、真反例(TN)、假反例(FN)，它們存在關系：TP+FP+TN+FN=數據集樣本數.

真正例(TP)：預測類別為正例，且真實類別也為正例的數據.

假正例(FP)：預測類別為正例，但真實類別為反例的數據.

真反例(TN)：預測類別為反例，且真實類別也為反例的數據.

假反例(FN)：預測類別為反例，但真實類別為正例的數據.

準確度：正確檢測出的正例和反例樣本數除以測試集的全部樣本個數的百分比RI.

(10)

查準率：測試集中正例(或反例)的樣本被檢測為正例(或反例)的樣本數TP(TN)除以檢測出的正例(或反例)樣本數的百分比P.

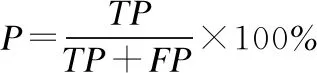
(11)

查全率:測試集中正例(或反例)的樣本被檢測為正例(或反例)的樣本數TP(TN)除以真實的正例(或反例)樣本數的百分比R.

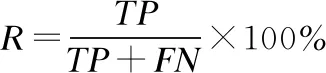
(12)

誤檢率：測試集中正例(或反例)的樣本被檢測為反例(或正例)樣本的個數FN(FP)除以測試集中所有正常樣本個數的百分比f.

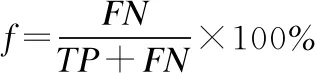
(13)

5.2 Fisher評分篩選的代表性維度

多步聚類中，每一步聚類對應一種劃分情形，并依據表2中對應劃分情形的代表性維度進行聚類.

表2 各劃分情形的代表性維度

5.3 聚類結果及分析

從表3可以看出，多步聚類過程中，自適應設參的改進DBSCAN聚類算法保持穩定的聚類簇數，達到每一步聚類的劃分目的.由于樣本數據劃分依據二分類的高Fisher評分維度，聚類中的樣本數據在空間呈現類二分態.改進的DBSCAN算法基于空間密度分布，判斷出樣本數據的類二分態分布，進而自適應設定出較準確的聚類參數，使得聚類簇數基本滿足劃分需求.雖然Step 2中的簇數為3，但大簇是Dos類，兩小簇主要是Probe類.同時，由于最小包含點數(MinPts)和掃描半徑(Eps)參數得到較準確的設置，改進的DBSCAN算法穩定保持低的噪聲率和較高的準確度，表現出良好的聚類性能.

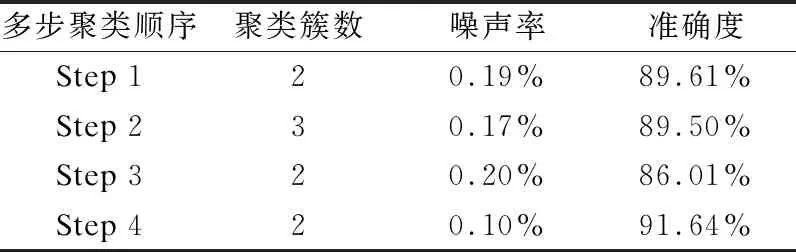
表3 聚類算法的性能

表4是統計混淆矩陣，顯示測試集在分布聚類后的詳細檢測結果.表中樣本數總和為22435，不計入噪點數109，故與測試集樣本總數22544不同.由表4可知，U2R被誤檢為Normal的情況較多，且在劃分后的U2R中，非U2R樣本的Normal占比高.由于U2R與Normal類樣本的特征值較相似，導致在空間分布中較接近，提高了準確檢測的難度.

表4 聚類的劃分結果

由表5數據可知，聚類結果中各類數據的查準率和查全率較均衡地處于90%左右，劃分效果較為均衡，保證檢測各類數據的較好性能，這是多步聚類相較于單步聚類(或分類)的優點.同時，劃分5個類別數據的誤檢率較低，其中的Normal類最低，說明算法能較好地避免正常網絡行為被誤判.

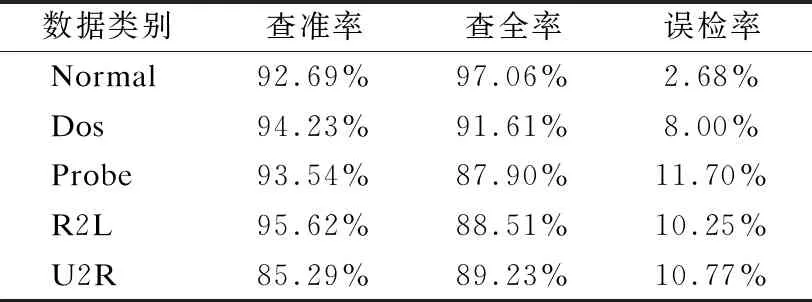
表5 聚類結果整體度量

從表6可知，對于檢測罕見攻擊U2R類，多步檢測方法的查準率和查全率均比單步檢測方法高，檢測結果的更準確.而單步檢測方法的檢測效果較一般，這是單步檢測的普遍現象.由于訓練集和測試集中U2R的樣本量少，且U2R樣本和Normal樣本在空間分布上較接近，單步檢測很難做到既檢測好Normal、Dos、PROB、R2L類，又檢測好U2R類.而在多步檢測中，可以通過先檢測出其他類的數據樣本，進而提高U2R類在待檢數據中的比例；還能在個別步驟中僅選取能夠良好劃分U2R類和Normal類的維度，使兩者在聚類空間中盡量分離.因此，多步檢測的檢測效果更好.

表6 檢測NSL-KDD數據集中U2R類的效果比較

6 結 語

在不同的網絡行為數據集中，多步檢測順序的確定，以整體檢測效果好壞作為判斷標準.其中，整體檢測效果的評價需要可量化的計算方法.改進Fisher評分是一種可量化的計算方法，其對維度評分的大小等于維度劃分能力的大小，而維度劃分能力的大小與檢測效果成正比.通過計算并統計不同劃分順序的維度劃分能力總分，即可以總分高的劃分順序作為多步檢測順序.因此，基于改進Fisher評分確定多步檢測順序的方法，在不同的網絡行為數據集中都能被應用.

在改進Fisher評分自動確定代表性特征和確定多步聚類檢測順序的基礎上，將基于最小二乘法擬合原理和曲線擬合的拐點半徑計算，應用于DBSCAN聚類中感知判斷網絡行為數據的空間分布態，以判斷結果實現自適應設置聚類參數，實現網絡行為數據的自動合理地聚類，提高入侵類別檢測算法的自動化程度和智能性.同時，該檢測算法較有效地解決非平衡網絡行為數據中全類別檢驗難的問題.該檢測算法能在保證良好檢測效果的情況下，適應復雜的網絡行為數據變化，減少算法使用難度，具有較高的應用價值.

在維度的Fisher評分實驗中，僅對兩種劃分順序進行比較，未能夠明確得出最合理的劃分順序.同時，在改進DBSCAN聚類算法的自適應設參階段中，數據量越大，曲線擬合的時間越長，影響檢測速度.因此，如何判斷最合理的劃分順序以及提升曲線擬合效率是下一步研究的重點方向.