具有吸毒年齡和治療年齡的海洛因模型的全局穩(wěn)定性

劉俊利

(西安工程大學(xué)理學(xué)院，西安 710048)

1 Introduction

Illicit opioid use can cause significant public health problems, which have been identified in many countries across the globe[1]. Dependent heroin or other opioid users continue to use opioids despite the significant social and health problems. Research in Europe and the United States indicates that dependent heroin users, who seek treatment, may continue to use heroin for decades[2-4]. After completing a given episode of drug treatment, the majority of drug users will relapse to heroin use[5]. Heroin had long been the primary drug of abuse in China since the reemergence of the drug problem in the country in early 1980s[6]. In addition to their deleterious somatic and psychological effects, heroin abuse and dependence may result in the transmission of human immunodeficiency virus (HIV) and hepatitis C virus (HCV)[7,8]. Treatment of heroin/morphine users and users of other drugs such as cocaine is a costly procedure and is a major burden on the health system of any country. Mathematical models are important tools for studying the spread and control of infectious disease, and as such, could hopefully becomes a useful technique to aid specialists in devising treatment strategies. Although much have been done in terms of modeling and analysis of disease transmission, little has been done to apply these techniques to the emerging heroin epidemics.

In fact, the spread of heroin habituation and addiction can be well modeled by epidemic-type models as “transmission” occurs in the form of peer pressure where established users recruit susceptible individuals into trying and using the drug. Recently,White and Comiskey[9]proposed a standard model, comprised of three state variables corresponding to susceptibles, heroin users, and heroin users in treatment. The basic reproduction number R0is proposed, sensitivity analysis is performed on R0, the stability of the system is investigated in terms of R0. Mulone and Straughan[10]further discussed the stability of the positive equilibrium of the White and Comiskey[9]model for heroin epidemics. Motivated by the works of White and Comiskey[9]and Mulone and Straughan[10], several heroin models have been developed based on the principles of mathematical epidemiology. Wang et al[11]proposed a system of ordinary differential equations(ODEs)to model the spread of heroin,and studied the global stability of the disease-free equilibrium and the positive equilibrium by using the second compound matrix. Liu and Zhang[12]considered the delay effect in those returning to untreated drug taking from a treatment programme,they assumed that the time needed to return to untreated drug varies according to drug users’ different temporal, social, and physical contexts, they proposed a delay differential equation, where distributed delay was introduced in the relapse term. The global dynamics of [12] was also investigated in[13]by constructing appropriate Lyapunov functional. Fang et al[14]presented a heroin epidemic model with two distributed delays, one is the progression-to-use time delay to describe the time needed for a susceptible individual to become an infectious heroin user. The other is the relapse delay to describe the time needed for a treated drug user to return to untreated drug user. The global asymptotic stability of the heroin epidemic model was obtained by the method of Lyapunov functional. To investigate seasonal variations in heroin epidemic,Samanta[15]considered a nonautonomous heroin epidemic model, using the method of Lyapunov functional, some sufficient conditions are derived for the global asymptotic stability of the system.

Age structure is also an important characteristic in the modeling of some infectious diseases. In general, there are two different age structures in disease models: biological age and infection age[16]. Two types of age-related models exist in the literature; that is, age-structured models[17,18]and age-of-infection models[19-21].

Age-related models are normally has the form of partial differential equations(PDEs) or integro-differential equations, therefore, their dynamical analyses are more difficult than those of the ordinary differential equations models. To investigate the influence of the age on the spread of the heroin epidemic, Fang et al[22]presented a heroin epidemic model with age-dependent susceptibility, the global dynamics was obtained by using a suitable Volterra type Lyapunov function. Fang et al[23]studied the influence of the treat-age for the heroin users during the treatment, the global dynamics was investigated by constructing a class of global Lyapunov functional. Infectivity experiments have suggest that the importance of variable infectivity in the spread of infectious diseases[24], hence it is important in modeling heroin to track the infection age of drug users.

In this paper, we will develop a heroin model with both the infection age of drug users not in treatment and the treat age of drug users in treatment. Our model is different from the one proposed in[22], which incorporates the biological age of susceptile individuals in modeling heroin. For our heroin model, the basic reproduction number R0is defined. R0was proved to be a threshold determining whether or not the disease dies out. Specifically, if R0< 1, there exists only the disease-free steady state which is globally asymptotically stable by applying the fluctuation lemma; and if R0> 1,then there is a unique endemic steady state that is globally asymptotically stable by constructing suitable Lyapunov functional and the disease persists at the endemic level.The Lyapunov functional we used is of the same type as those in [16,20,25–28].

This paper is organized as follows. In the next section, we give the underlying assumptions and formulate the PDE heroin model. In section 3,we study the existence of steady states,calculate the basic reproduction number,and analyze the local stability of steady states. In the following section, we establish the threshold dynamics of the model in terms of the basic reproduction number. We conclude in section 5 with a discussion.

2 Model formulation

Let S(t) denote the number of susceptible individuals at time t ≥0, we call the time from becoming drug users to present the infection age and denote it by a, then U1(t,a) denote the number of drug users not in treatment at time t with infection age a, and U2(t,c) denote the number of drug users in treatment at time t, c ≥0 denotes the treat age of the heroin drug users undergoing treatment at time t. Consider a PDE heroin model as follows

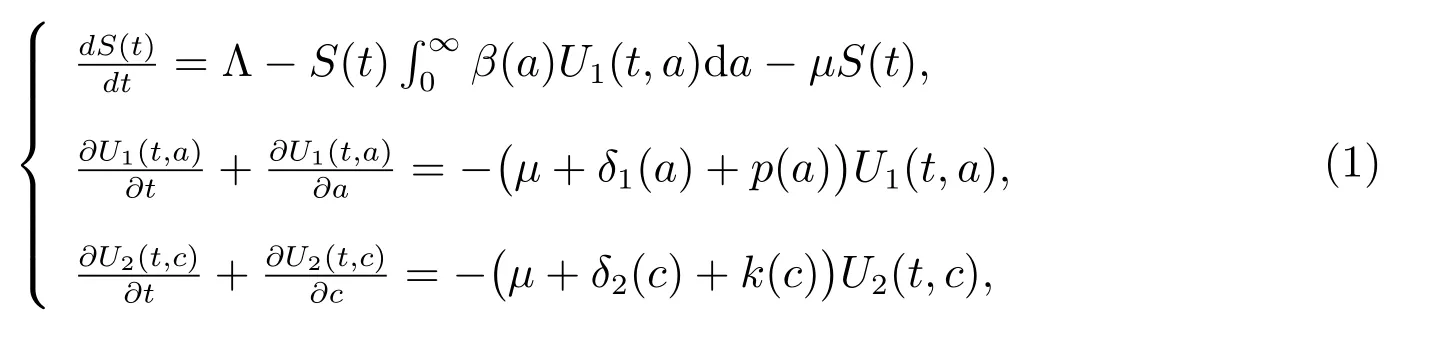
with boundary conditions

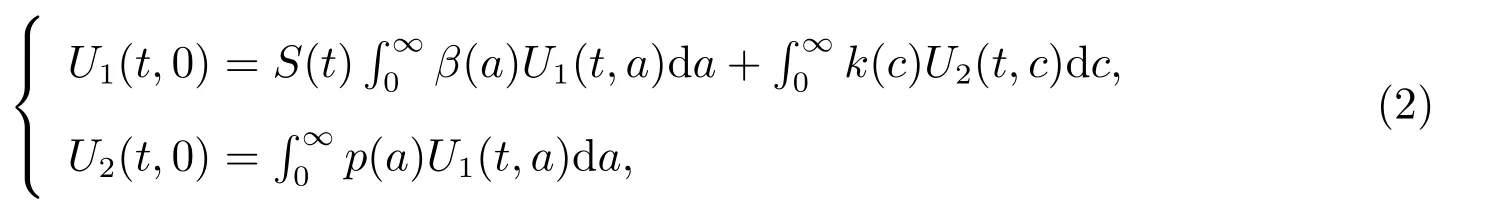
and initial conditions

The meanings of all parameters in (1) are as follows:

Λ: The constant recruitment entering the susceptible population;

μ: The natural death rate of the general population;

δ1(a): A removal rate with infection age a that includes drug-related deaths of users not in treatment and a spontaneous recovery rate; individuals not in treatment who stop using drugs but are no longer susceptible;

δ2(c): A removal rate with treat age c that includes drug-related deaths of users in treatment and a rate of successful“care”that corresponds to recovery to a drug free life and immunity to drug addiction for the duration of the modeling time period;

β(a): The probability of becoming a drug user at infection age a;

p(a): The probability of drug users with infection age a who enter treatment;

k(c): The probability of a drug user in treatment with treat age c relapsing to untreated use.

For system (1), we make the following hypotheses about the parameters.

(H1): Λ, μ>0.

(H2): k, p, β ∈CBU(R+,R+), where CBU(R+,R+) is the set of all bounded and uniformly continuous functions from R+to R+.

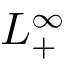
(H4): For any a > 0, there exists aβ, ap> a such that β is positive in a neighbourhood of aβand p is positive in a neighbourhood of ap.

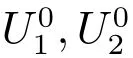
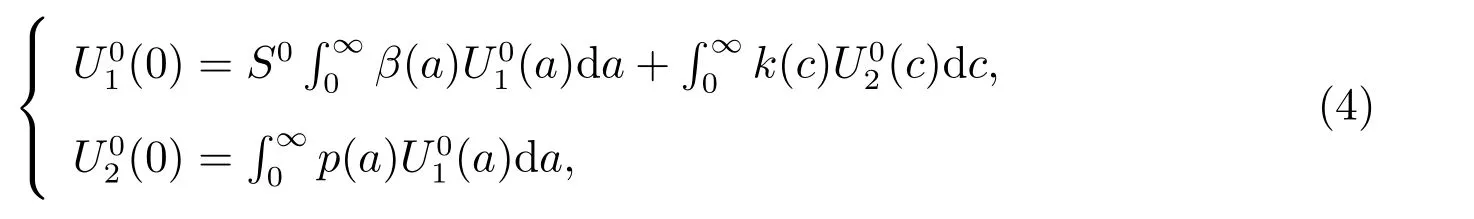
then (1) is well-posed.

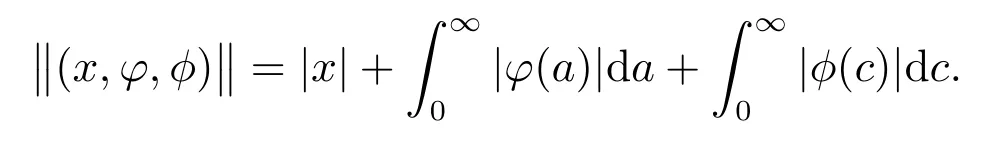
The norm has the biological interpretation of giving the total population size.

For a, c ≥0, let

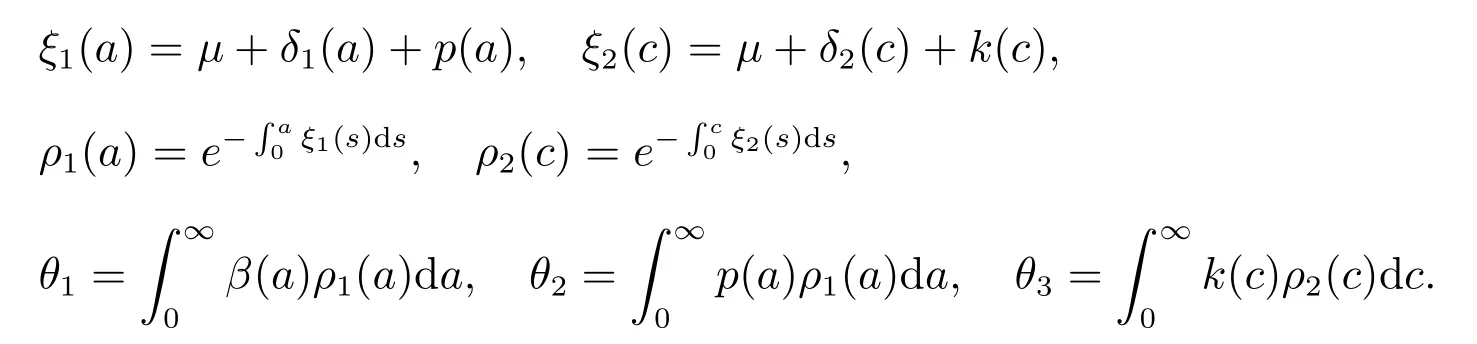
It follows from (H1), (H3) and (H4) that θ1>0 and is finite, 0<θ2<1, 0 ≤θ3<1.

We follow [17] and integrate the equations for U1and U2in (1) along the characteristic line t ?a=constant and t ?c=constant, respectively, we obtain

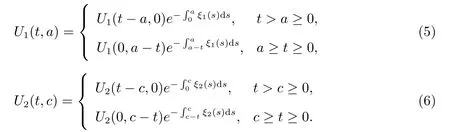
Using standard methods we can verify the existence, uniqueness, non-negativity of solutions to model (1) with the boundary conditions (2) and initial conditions (3) (see[17,29]). Furthermore, system(1)defines a continuous solution semiflow Φ:R+×X →X by

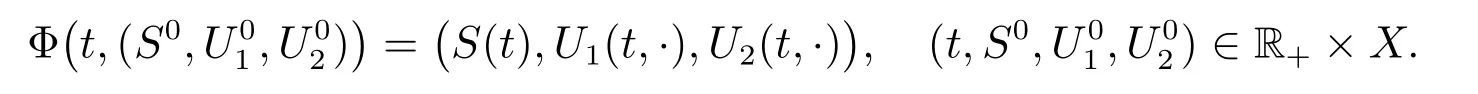
Let

Then by (1), (2), (5) and (6), we have

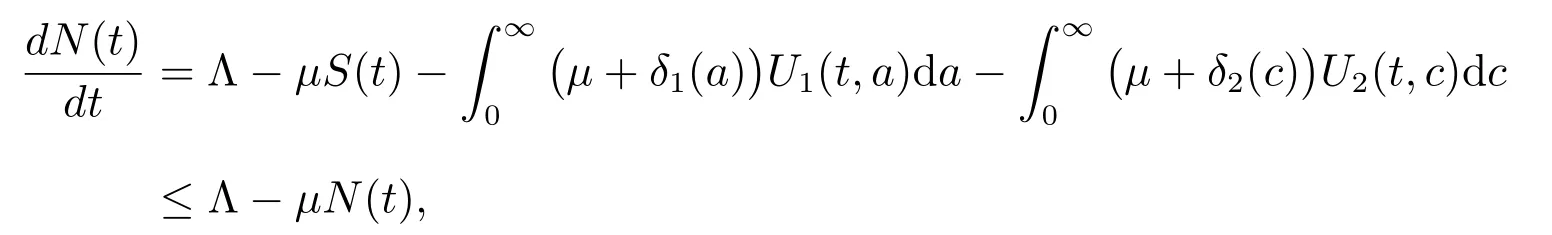
Denote

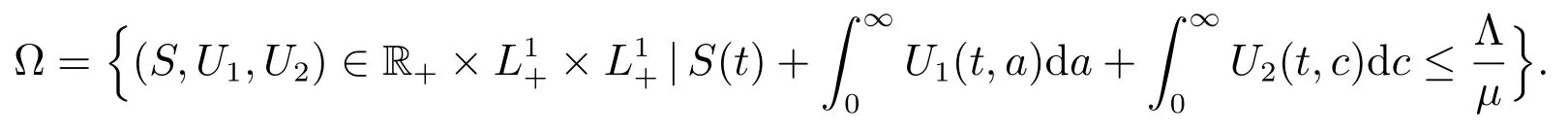
We know ? is a positively invariant and attractive set for system (1).

Then if we consider the limit behaviour of (1), we only need to consider solutions of (1) with initial conditions in ?.

3 Steady states and their local stability

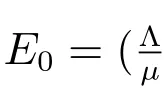
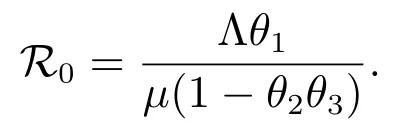
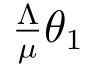
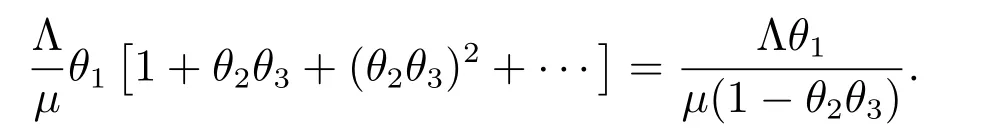
Thus, R0is the basic reproduction number[31,32], and acts as a threshold as is shown in section 5.

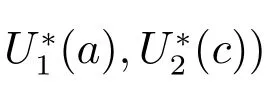
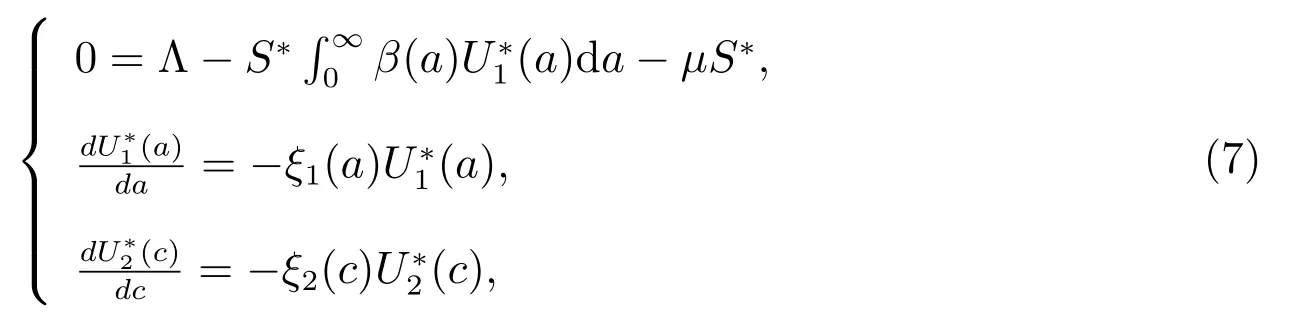
with boundary conditions

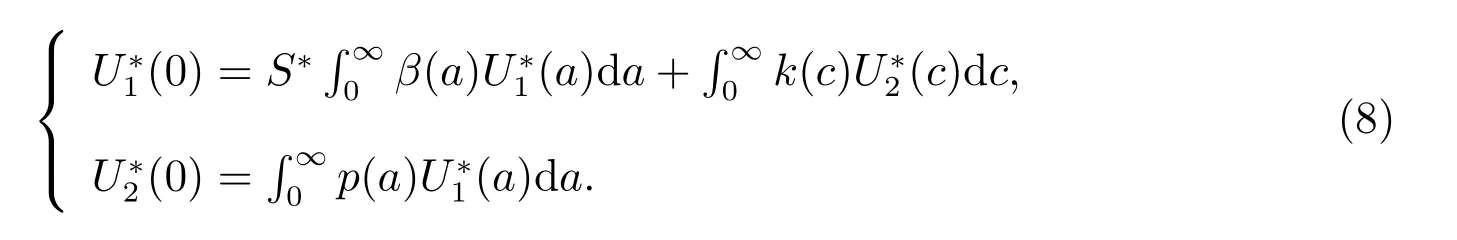
Then from the second equation of (7), we have

By using the third equation of (7), the second equation of (8) and (9), we get

Substituting (9) into the first equation of (7), we obtain

Substituting (9)–(11) into the first equation of (8) gives

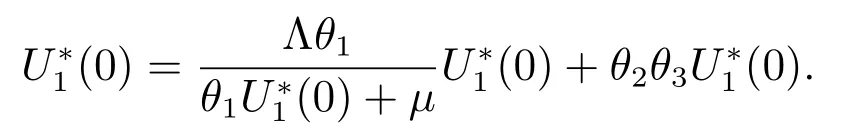
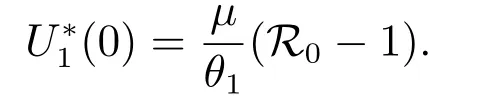
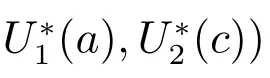
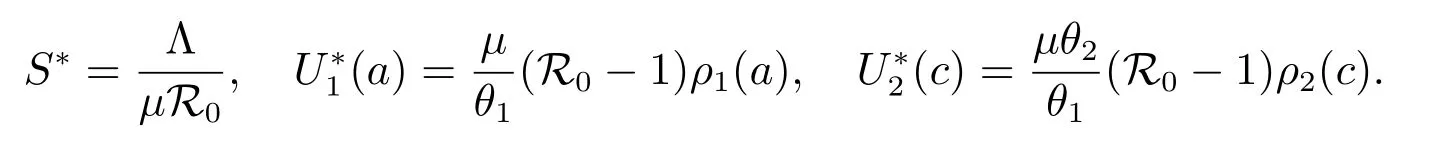
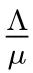
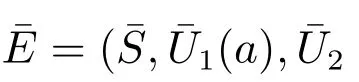
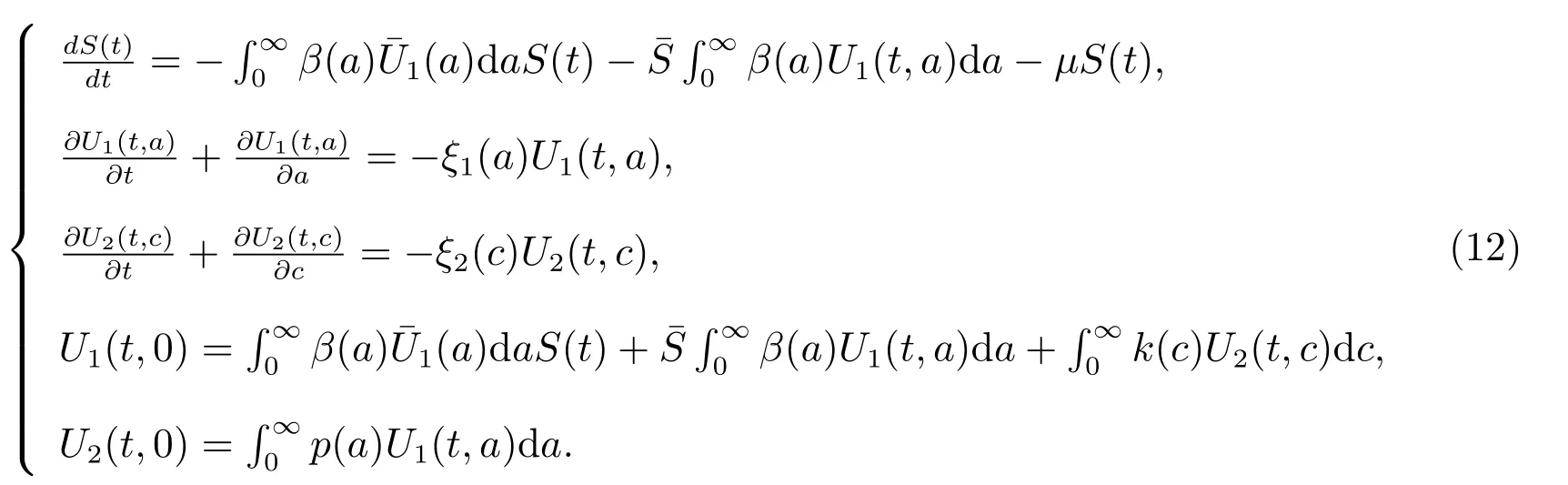
S(t)=x0eλt, U1(t,a)=y0(a)eλt, U2(t,c)=z0(c)eλt,

then substituting them into (12), we get

Then the solution of (13) satisfies the characteristic equation

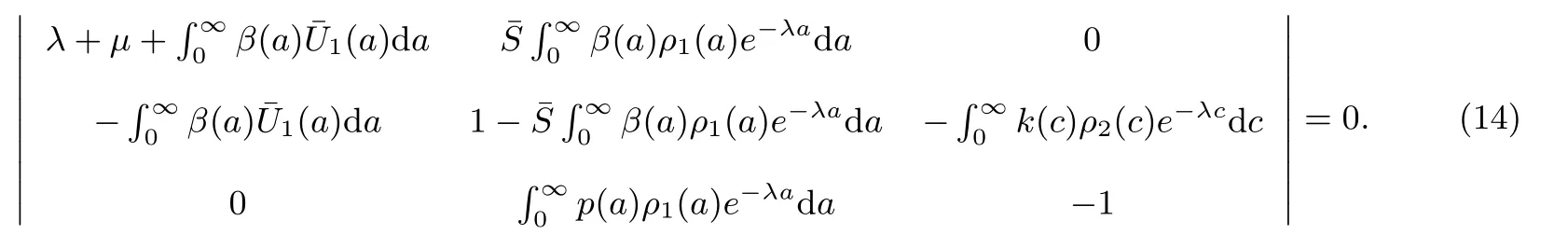
Theorem 2The following statements are valid:

Proof1) By (14), the characteristic equation at E0is

where

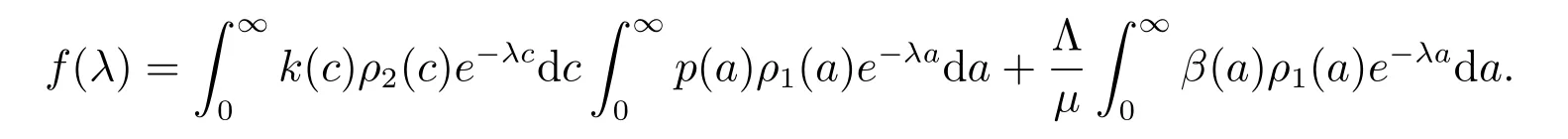
Clearly, ?μ is a root of (15), and the other roots of (15) is determined by f(λ) = 1.Note that f(λ) is a continuously differential function and

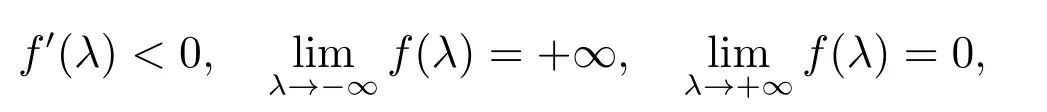
then f(λ)=1 has a unique real root λ?. Since

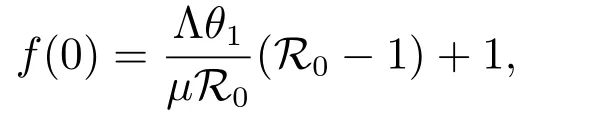
then λ?<0 if R0<1, and λ?>0 if R0>1. Hence the disease-free steady state E0is unstable if R0>1.

If R0<1, let λ=x+iy with x,y ∈R be a root of f(λ)=1. Then we have

1=|f(λ)|=|f(x+iy)|≤f(x),

which means that λ?≥x, thus all roots of f(λ) = 1 must have negative real parts.Therefore, E0is locally asymptotically stable if R0<1.

2) By (14), the characteristic equation at E?is

where

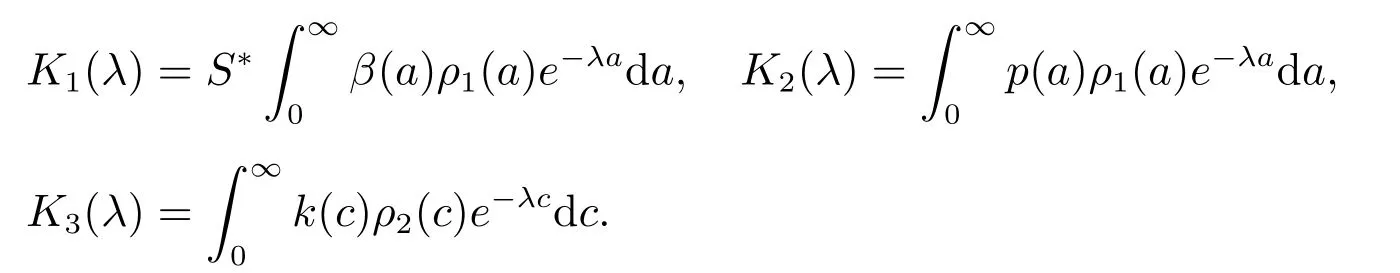
The modulus of the right-hand side of (17) satisfies

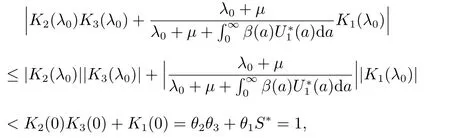
the last inequality follows from the fact that

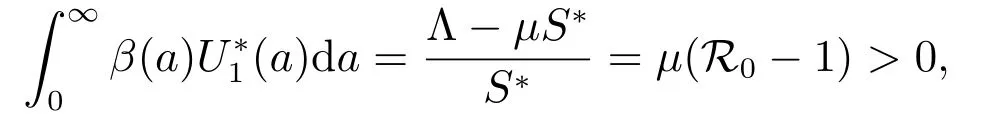
which is a contradiction to (17). This means that all roots of (16) have negative real parts. Therefore, E?is locally asymptotically stable if R0>1.

4 Global asymptotic stability of the steady states

In this section, we study the global stability of the steady states. First we prove the global stability of the disease-free steady state by applying the fluctuation lemma.

Lemma 1[33]Let h:R+→R be a bounded and continuously differential function.Then there exists sequences {sn} and {tn} such that sn→∞, tn→∞, h(sn) →h∞, h(tn)→h∞, h′(sn)→0 and h′(tn)→0 as n →∞.

The following theorem states that the disease dies out eventually if the basic reproduction number is less than unity.

ProofBy Theorem 2,we only need to show that E0is globally attractive. Recall that

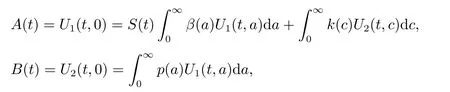
we then get

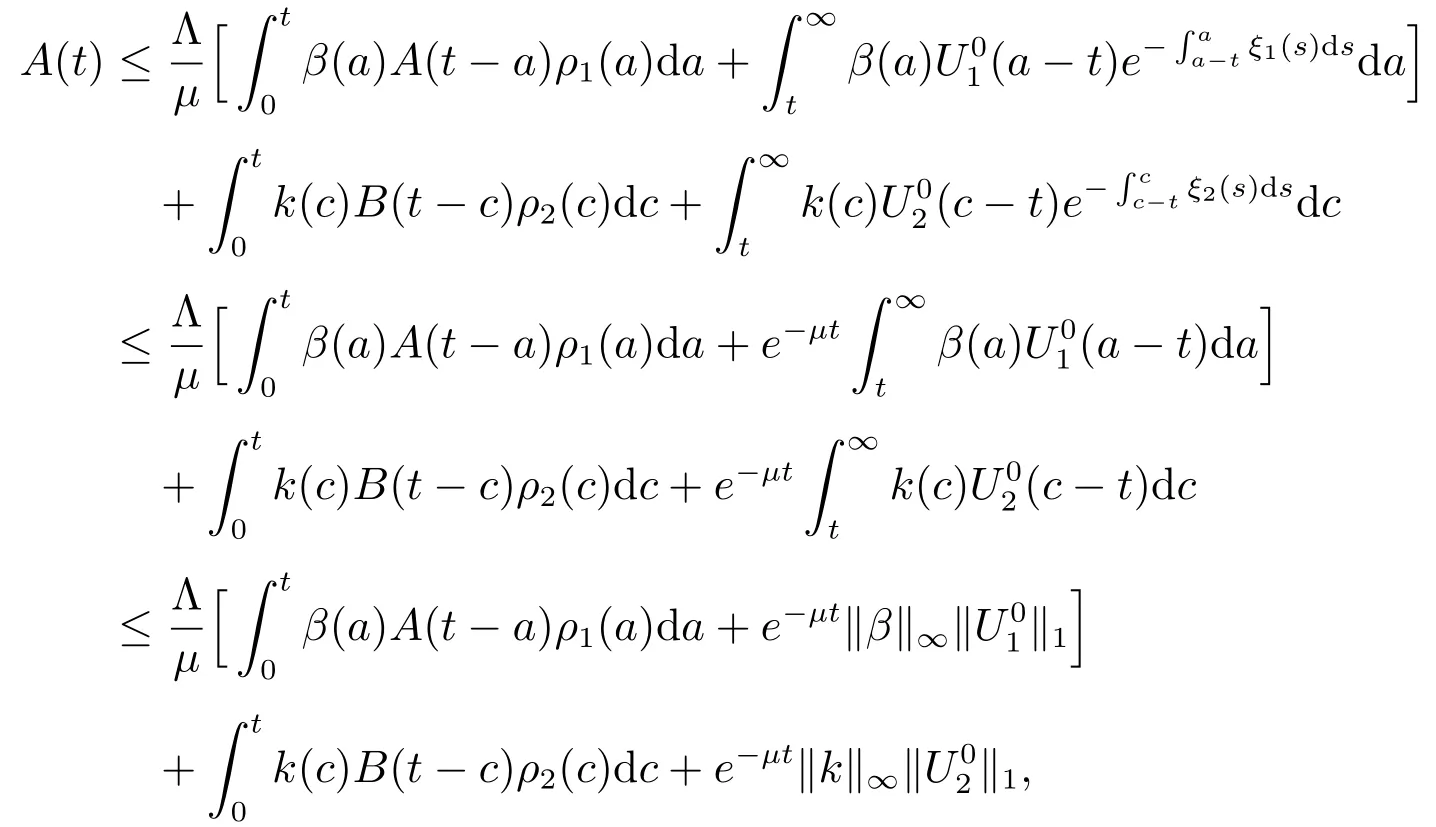
and

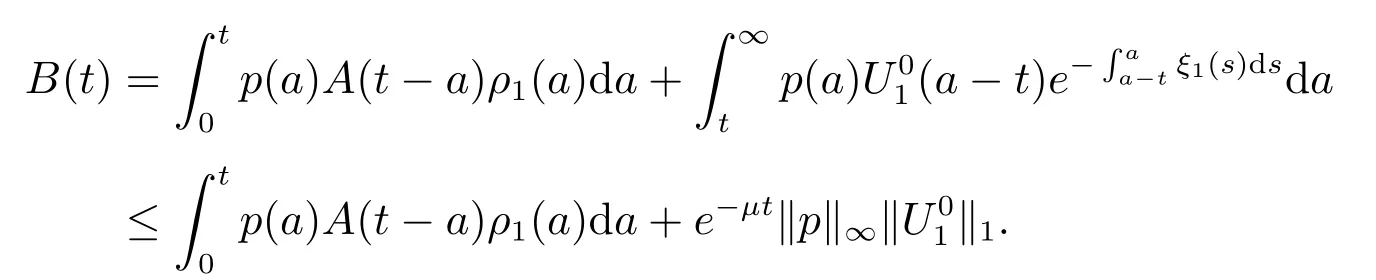
It follows that

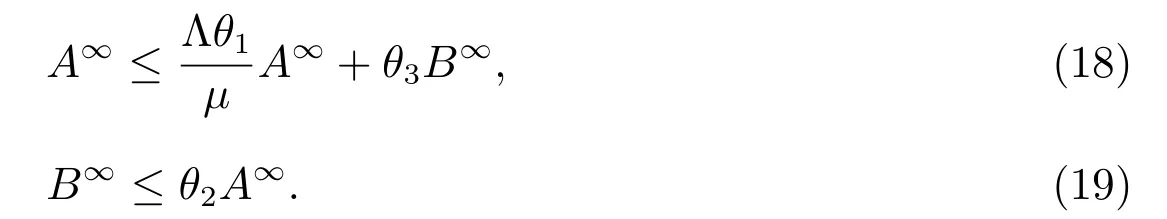
Hence, (18) and (19) together yields

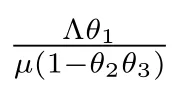
By (5), we get

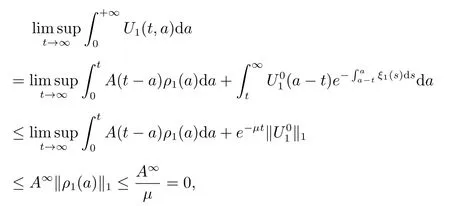
which implies that

similarly, we have

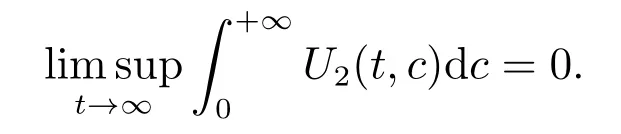
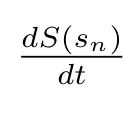
We now prove the global stability of the endemic steady state by constructing suitable Lyapunov functional. The following result shows that if R0> 1, the disease persists at the unique endemic steady state level.

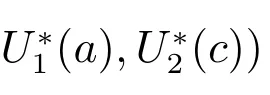
ProofAgain by Theorem 2, it suffices to show that E?is globally attractive.Define

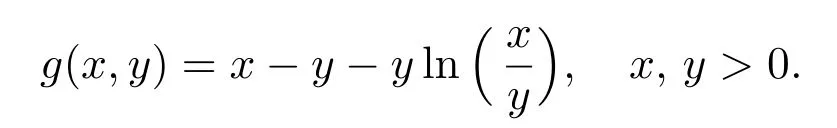
Construct a Lyapunov functional V =V1+V2+V3with

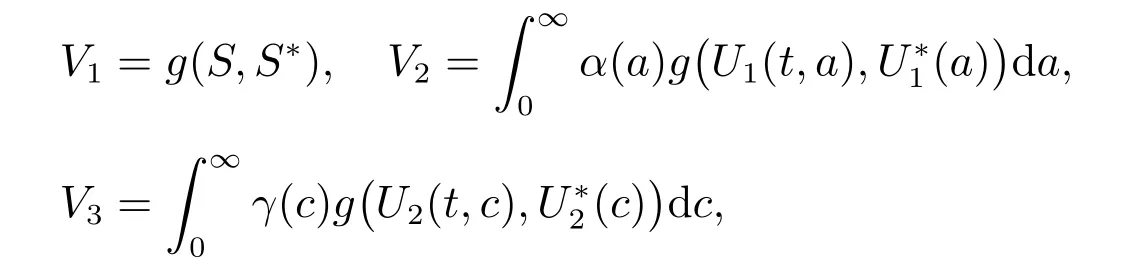
where nonnegative functions α(a) and γ(c) are given by

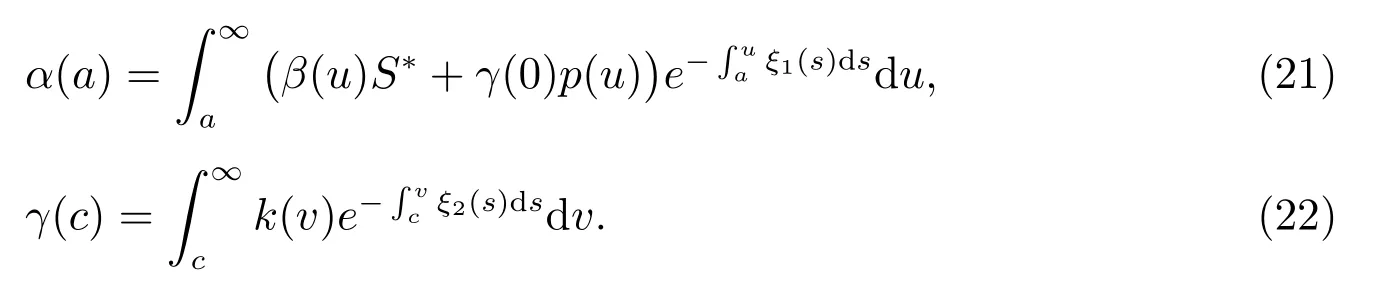
Using the steady state equations (7), differentiating V1along the solutions of (1)gives

Similar proof as those in [16], we have the following results

It follows from (21) and (22) that

α′(a)=ξ1(a)α(a)?(β(a)S?+γ(0)p(a)), γ′(c)=ξ2(c)γ(c)?k(c).

Also notice that γ(0)=θ3and α(0)=θ1S?+θ2θ3=1, hence, we have

Hence, adding (23)–(25) together yields

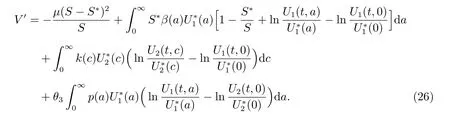
Here, we have used the equality

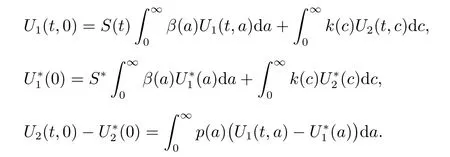
Notice that

and

Adding (26)–(28) together yields

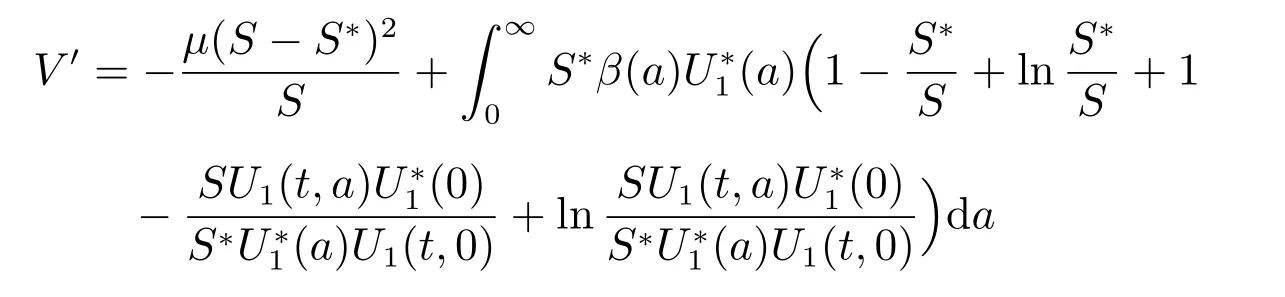
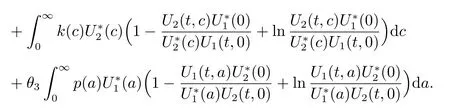
Since 1 ?x+ln x ≤0 for x > 0 with equality holding if and only if x = 1. Hence,V′≤0, and V′=0 implies that S =S?and

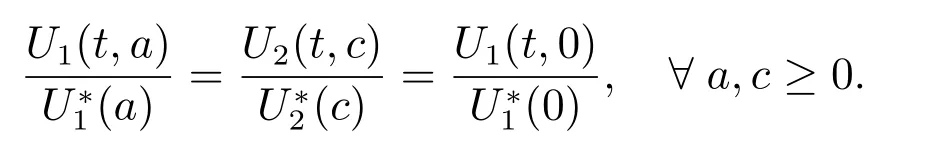
It can be verified that the largest invariant set where V′= 0 is the singleton {E?}.Therefore,the endemic steady state E?is globally asymptotically stable in ?0if R0>1.This completes the proof.

5 Discussions

In this article,a PDE heroin model(1)is proposed here to incorporate the infectionage of drug users not in treatment and the treat-age of drug users in treatment. We have shown that the global dynamics of (1) is determined completely by the basic reproduction number R0. The disease dies out if R0< 1 and the disease persists if R0> 1. Fluctuation lemma is used to show the global stability of the disease-free steady state. Following the construction of Lyapunov functionals used in [16], one Lyapunov functional is constructed to show the global stability of the endemic steady state.

For a given set of parameters, a sensitivity analysis of R0could be used to guide disease control strategies. The aim of our model is to identify parameters of interest for study in the drug-using career, our results can be used to inform and assist policymakers in targeting prevention and treatment resources for maximum effectiveness.

Suppose β(a) = β, δ1(a) = δ1, δ2(a) = δ2and p(a) = p for some β, δ1, δ2, p > 0.Let

represents the total number of drug users not in treatment at time t, then system (1)becomes

with boundary condition

for t ≥0. This model is a special case of our model (1), it was proposed in [23], the global behaviour of system (29) was resolved in [23]. Our global stability results also provide the global dynamics for (29).