朗伯-比爾定律的適用條件與限制

辛伍紅

(山東理工大學 分析測試中心，山東 淄博 255000)

物質對光吸收的定量關系很早就引起了科學家的注意。皮埃爾·布格和約翰·海因里希·朗伯分別于1729年和1760年闡明了物質對光的吸收程度和吸收介質厚度之間的關系。1852年奧古斯特·比爾進一步提出了光的吸收程度和吸光物質濃度也具有類似關系。兩者結合起來就得到了有關光吸收的基本定律——布格-朗伯-比爾定律，簡稱朗伯-比爾定律(Lambert-Beer law)，這一定律是分光光度法的基本定律和定量基礎[1-3]。

然而，朗伯-比爾定律是一個有限定律，入射光單色性差、溶質和溶劑的性質等均會導致偏離。例如，比爾定律只適用于稀溶液，因為濃度高時，吸光物質粒子平均距離減小，相互作用增強，受粒子間電荷分布相互作用的影響，摩爾吸收系數ε發生改變，導致偏離。因此，分光光度法的實驗是基于關鍵定律適用的情形進行設置的[4-8]。在實驗教學的過程中，研究者發現多數學生存在對適用條件不甚理解的情況。因此，本論文以紫外分光光度法測量布洛芬含量為例，分析定律適用條件對實驗設置的影響，提高學生理論聯系實際的能力[9, 10]。

1 朗伯-比爾定律的適用條件

朗伯-比爾定律描述了物質對光的吸收程度和吸收介質厚度、吸光物質濃度間的正比關系，其數學表達式如下[9]：

A=εbc=lg(1/T)

(1-1)

A為吸光度；ε為吸光系數，為常數；b為吸收層厚度；c為物質的濃度；T為透光率，T=It/I0，其中It為透射光強度，I0為入射光強度。

其物理意義是當一束平行單色光垂直通過某一均勻非散射的吸光物質時，其吸光度A與吸光物質的濃度c及吸收層厚度b成正比。具體適用條件如下：

(1) 入射光為平行單色光且垂直照射；

(2) 吸光物質為均勻非散射體系；

(3) 吸光質點之間無相互作用；

(4) 輻射與物質之間的作用僅限于光吸收，無熒光和光化學現象發生；

(5) 吸光度在0.2～0.8之間。

根據適用條件(3)和(4)，當被測物與溶質無相互作用、與輻射間僅存在吸收作用時，以下公式成立：

I0=Ia+It+Ir

(1-2)

Ia為吸收光強度；Ir為反射光強度。

適用條件(2)中非散射體系的限制使Ir=0，公式(1-2)可以簡化為：

I0=Ia+It

(1-3)

此時公式(1-1)中對T的定義成立。

通過上述討論可以看出，朗伯-比爾定律適用條件(2)～(4)是針對實驗體系做出的限制。本論文以布洛芬的氫氧化鈉溶液為待測物，在該體系中，吸光物質為均勻非散射體系、吸光質點間無相互作用、輻射(紫外光)與物質間僅存在光吸收，滿足適用條件(2)～(4)。以下討論適用條件(1)和(5)成立的情形。

2 適用條件(1)的成立

紫外可見分光光度計主要由光源、單色器、樣品池和檢測器四個部分組成。其中單色器是指將光源發出的光分離成所需要的單色光的器件，由入射狹縫、準直鏡、色散元件和出射狹縫構成。入射狹縫用于限制雜散光進入單色器；準直鏡將光源發出的發散光變成平行光；色散元件是單色器的關鍵部件，作用是將復合光分解成單色光；出射狹縫用于限制通帶寬度。可以看出，光源發出的混合光經單色器作用后滿足適用條件(1)的“平行”和“單色光”描述。值得注意的是，“垂直照射”這一條有非常重要的限定作用。如圖1所示，當光垂直照射在樣品池表面時，可以通過樣品池的厚度描述吸收層厚度b。而非垂直照射時，不但在樣品池表面會發生反射Ir≠0，導致朗伯-比爾定律不成立，入射角度的差異也會影響吸收層的厚度。可見，在保證儀器穩定性的前提下，當樣品池表面與色光通路垂直時，適用條件(1)成立。

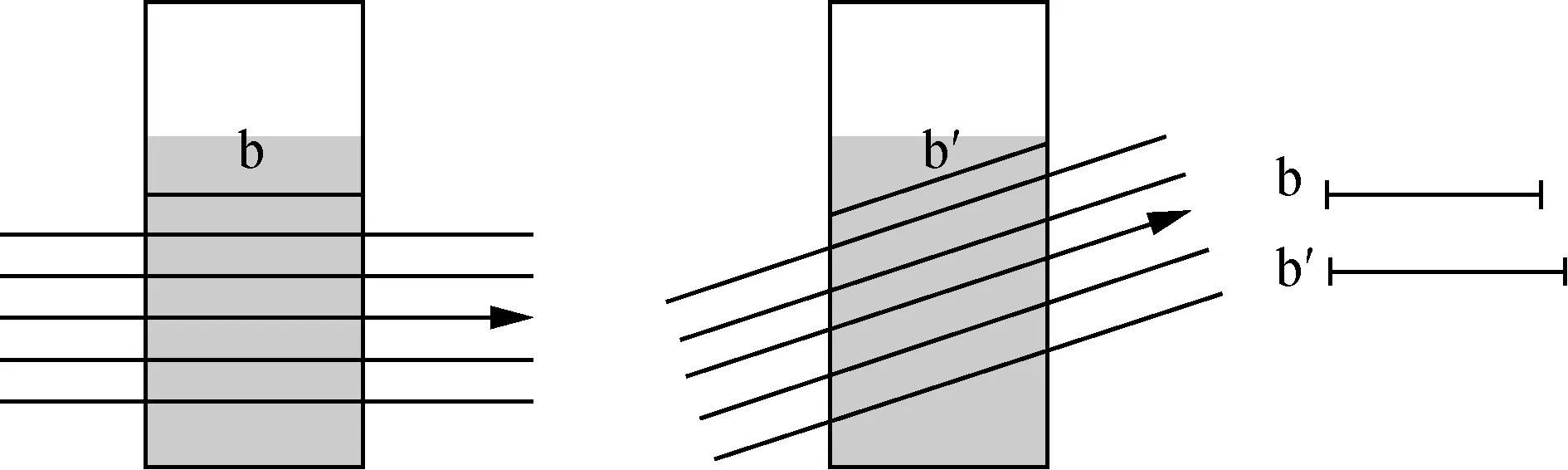
圖1 入射光垂直照射和非垂直照射時吸收層的厚度示意圖

3 適用條件(5)的成立

為了進一步理解適用條件(5)中對吸光度值限定的意義，分別配制標準溶液和參照溶液組。

3.1 標準溶液和參照溶液的配制

準確稱取250 mg布洛芬標準品，溶于0.4%氫氧化鈉溶液中，定容至50 mL，得到濃度為5 mg/mL的標準儲備液。用移液管分別移取5、10、15、20和25 mL的標準儲備液，用250 mL容量瓶定容，稀釋溶劑為0.4%氫氧化鈉溶液，制成0.10、0.20、0.30、0.40和0.50 mg/mL的標準溶液。

用移液管分別移取30、35、40、45和50 mL的布洛芬標準儲備液，用250 mL容量瓶定容，稀釋溶劑為0.4%氫氧化鈉溶液，制成0.60、0.70、0.80、0.90和1.00 mg/mL的參照溶液。

3.2 測試及結果討論

首先將標準溶液加入樣品池中進行全波長掃描，獲得吸收曲線并讀取吸收峰對應的波長。圖2所示為布洛芬標準溶液的吸收曲線，從圖中可以觀察到三個明顯的吸收峰，分別位于226、264和272 nm。在分光光度法中，光吸收程度最大處叫做最大吸收波長，用λmax表示。根據定律，溶液濃度不同時，光吸收曲線的形狀相同，λmax不變，只是吸光度與濃度成正比關系變化。依據此定義判斷布洛芬氫氧化鈉溶液的λmax。

首先研究不同波長處標準溶液和參照溶液組中物質濃度與吸光度間的關系，實驗結果如圖3所示。圖3a為不同濃度布洛芬溶液在226 nm處的吸光度值，此時物質的吸光度與濃度不成線性關系，說明在226 nm處朗伯-比爾定律不成立，不符合λmax的定義。進一步研究264和272 nm波長處的情況，結果如圖3b和3c所示。對標準溶液組(濃度0.10～0.50 mg/mL)而言，在264和272 nm處吸光度與濃度呈現良好的線型關系。根據定義，可以判斷264 nm為布洛芬氫氧化鈉溶液的λmax。

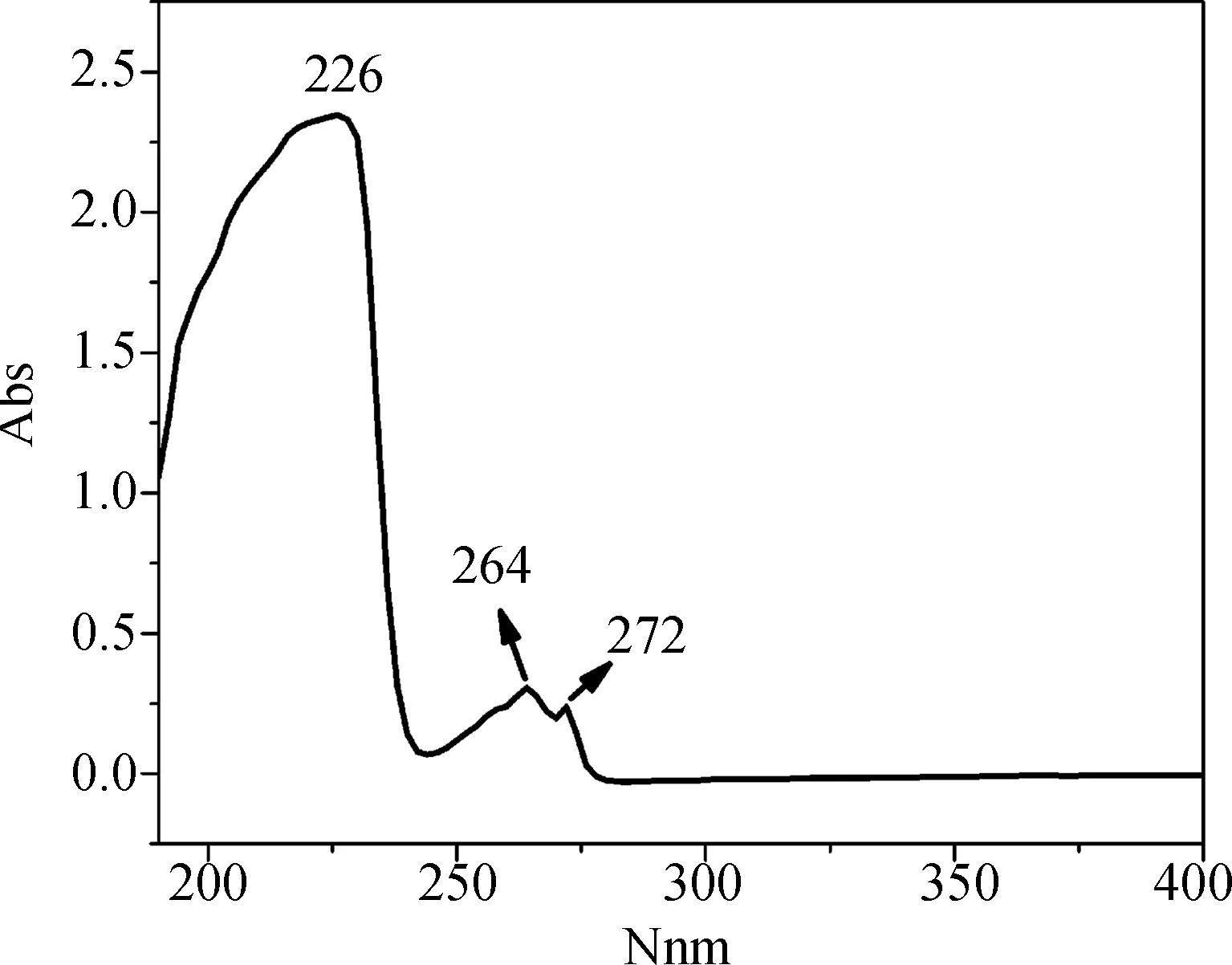
圖2 布洛芬標準溶液的吸收曲線

進一步對比264和272 nm處標準溶液和參照溶液組間吸光度與濃度的關系，可以看出當溶液濃度增大后，兩條吸收曲線均發生了負偏離。這主要是由于隨著濃度的增大，布洛芬溶液的ε減小，導致實際曲線向濃度軸偏離。圖3b和3c顯示了隨溶液濃度增大方差值(R2)的變化情況，可以用來指示實際曲線的負偏離程度。從R2的計算結果來看，在264和272 nm 處標準溶液組的吸光度-濃度曲線具有良好的線性(R2=0.999 9)。當溶液濃度進一步增大時，R2值逐步增大，負偏離程度不斷加劇。在實際應用中，正偏離或負偏離都對分光光度法分析的準確性有重大影響。通過適用條件(5)的限定，可以幫助實驗人員根據吸光度快速判斷ε穩定的濃度區間，評估分光光度法分析對體系的適用情況。進一步觀察圖3c中的曲線可以發現，當溶液濃度升高至0.60 mg/mL時，盡管吸光度值低于適用條件(5)定義的最大值0.8，但數據點間的線性程度下降，R2降低。說明適用條件(5)中對吸光度的限定主要針對的是λmax處，合理的選擇λmax很重要。

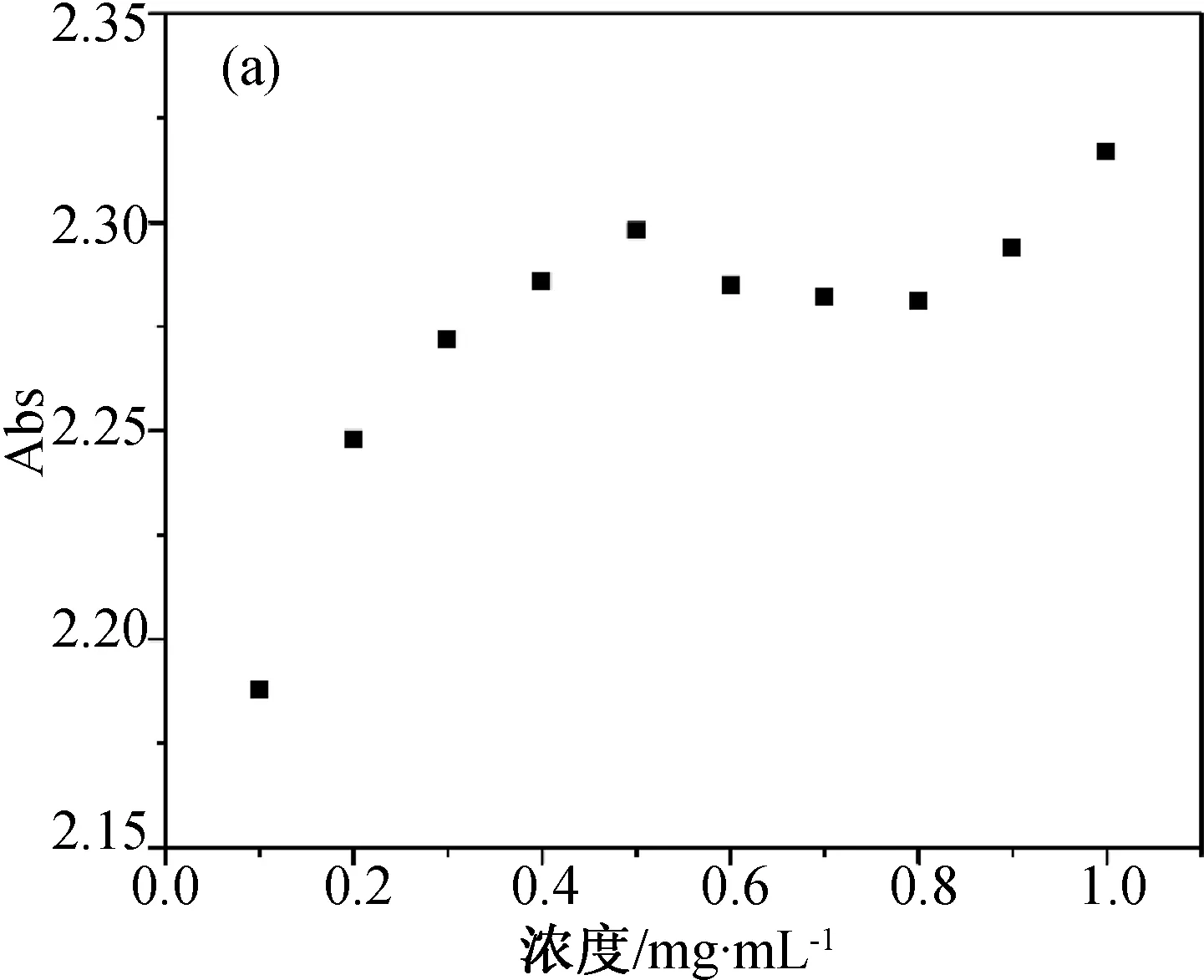
(a) 226 nm

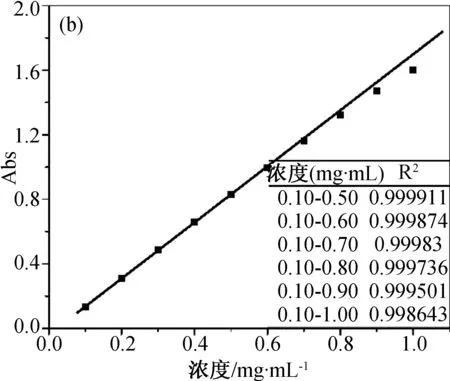
(b) 264 nm

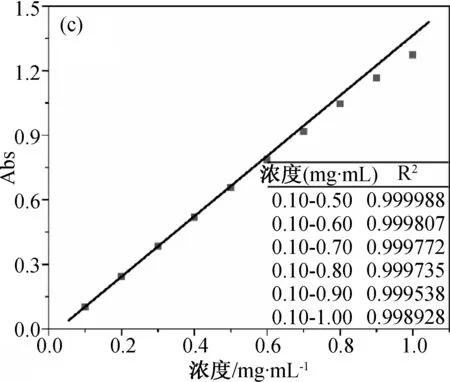
(c) 272 nm

根據本節的討論，在實際測試中，需要首先根據朗伯-比爾定律的定義選擇λmax，并進一步根據適用條件(5)選擇合適的標準溶液濃度區間，確保分光光度法分析的準確性。

4 結語

實驗教學的目的不僅在于培養學生的動手能力，更應側重培養學生理論聯系實際的能力。本論文從朗伯-比爾定律的定義和適用條件出發，以紫外分光光度法測量布洛芬含量為例，逐一研究適用條件限定的意義，明確分光光度法分析對體系的適用情況。通過這種逆向思考和講解的方式，將課本上平面的定律變為立體的定律，培養了學生對實驗方案的設計能力，體現了理論對實踐的指導作用。這種教學方式有利于提升學生對基礎理論的掌握，進一步激發學習熱情，有極佳的課程效果。