基于阻抗特性多項式擬合的直驅風電機組次同步振蕩穩定判據

于永軍，王利超，張明遠，肖仕武*，張馨元

基于阻抗特性多項式擬合的直驅風電機組次同步振蕩穩定判據

于永軍1，王利超1，張明遠2，肖仕武2*，張馨元2

（1．國網新疆電力科學研究院，新疆維吾爾自治區 烏魯木齊市 830011；2．華北電力大學電氣與電子工程學院，北京市 昌平區 102206）

近年來，阻抗分析法已成為分析新能源發電并網系統穩定性問題的一種主要研究方法。以直驅風電機組并網系統為例，分析了現有的奈奎斯特(Nyquist)穩定判據的特點和適用范圍。為了彌補現有阻抗穩定判據的不足，提出了一種基于阻抗特性分式多項式函數擬合的量化穩定判據，采用分式多項式函數等效擬合理論推導或實測的風電機組端口阻抗特性，在擬合頻段內分式多項式與原阻抗特性等價。通過求取擬合多項式零點獲得了系統振蕩頻率和阻尼水平，量化分析了系統穩定特性，拓展了阻抗穩定判據的適用范圍。最后，通過理論分析和時域仿真驗證了分式多項式擬合判據的正確性和有效性。

直驅風電機組(D-PMSG)；序阻抗特性；多項式擬合；次/超同步振蕩；穩定判據

0 引言

隨著風電、光伏等新能源的大量并網，送受端常規機組被大量替代，電網形態及運行特性發生顯著變化，系統電力電子化特征凸顯，易引發次/超同步振蕩(sub/super-synchronous oscillation，SSO)問題[1-5]。2011年以來，我國河北沽源地區發生了多起因雙饋風電機組與串補電網相互作用而引發的次同步振蕩，造成變壓器異常振動和大量風機脫網[6-7]。2015年7月1日，我國新疆某地區大規模直驅風電機組(direct drive permanent magnet synchronous generator，D-PMSG)在接入弱交流電網情況下發生了次同步頻率功率振蕩，甚至導致了臨近汽輪發電機組扭振保護動作停機，引發了國內外廣泛關注[8]。

阻抗分析法由于物理概念清晰，采用分區分析方法降低了維數，易于擴展到多臺風電機組系統，因而成為當前分析風電機組并網系統SSO穩定性的一種主要研究方法[9]。采用阻抗分析法首先要獲得風電機組和電網阻抗模型。當前，對系統進行阻抗建模的方式主要有同步旋轉坐標系()建模[10-13]和三相靜止坐標系()建模[14-15]。

采用坐標系建模的結果是一個二維阻抗矩陣模型，由于阻抗矩陣往往不能解耦，使得基于該方法的穩定性分析較為復雜[16]。為了克服建模的局限性和缺點，文獻[15]提出在坐標系下采用諧波線性化的建模方法，通過測量某一頻率下由電壓擾動而產生的同頻率電流響應來建立序阻抗模型。由于序阻抗模型在建立過程中不需要確定特定參考坐標系，因而它更適用于多機復雜系統的阻抗建模。

穩定判據主要包括基于阻抗特性的奈奎斯特 (Nyquist)判據[17]、范數判據[18]和聚合RLC電路法[19-20]。Nyquist判據因在實際工程應用中簡單、直觀而獲得了廣泛的應用，其根據電網和風電機組阻抗比值的奈氏曲線是否包含(-1，0)判斷系統穩定性，通過奈氏曲線與單位圓在復平面上的交點來獲得系統振蕩頻率和相位裕量。這種方法能夠很好地定性判斷系統絕對穩定性(穩定/不穩定)，但在獲取系統實際振蕩頻率和比較不同系統間相對穩定程度(哪個更穩定/不穩定)上稍顯不足。文獻[21]采用基于阻抗特性的Nyquist判據對雙饋風電機組的序阻抗模型進行分析，并獲得了系統的振蕩頻率和相位裕量，但沒有比較不同系統間相對穩定程度。范數判據僅能給出定性的穩定分析結果，無法量化分析系統穩定性，且使用起來較為復雜。聚合RLC電路法通過計算RLC等效二階電路中R、L、C的具體數值來獲得系統阻尼和振蕩頻率，從而量化分析系統穩定特性，其具有物理概念清晰、易于理解的優點；但它僅適用于振蕩頻率的鄰域內且阻尼很小的工況，一定程度上限制了其適用范圍。文獻[19]采用聚合RLC電路法量化分析了直驅風電機組并網系統的SSO特性，獲得了系統振蕩頻率和阻尼。文獻[22]比較分析了采用Nyquist判據和聚合RLC電路法對雙饋風電場并網系統量化穩定分析的結果，同時指出采用Nyquist判據分析所得系統振蕩頻率與實際頻率存在一定的偏差，并且無法提供系統的阻尼水平。

在實際應用中往往需要定量對比2種工況下系統振蕩頻率和穩定裕度的變化，以便進行系統參數的修改及控制策略的調整。鑒于此，本文提出了基于阻抗特性分式多項式函數擬合的量化穩定判據，采用分式多項式對理論推導或實測的阻抗特性進行擬合，在擬合頻段內分式多項式與原阻抗特性等價。討論了分式多項式擬合實現方法，根據分式多項式的零點給出系統的振蕩頻率及阻尼水平。最后通過對比算例分析結果和時域仿真結果來驗證穩定判據的正確性和有效性。

1 直驅風電機組并網系統序阻抗特性

1.1 風電機組序阻抗特性

直驅風電機組并網系統電路結構及內部控制如圖1所示，由于風電機組并網次同步振蕩主要受PWM逆變電路的影響，因此重點對并網逆變器進行分析。

圖1中：ia、ib、ic是風電機組逆變器出口電壓；a、b、c和a、b、c分別為風電機組并網點電壓和電流；dc是直流側輸入電壓；是直流側電容；電感f與電容f組成LC濾波電路；電網等值阻抗由電阻g與電感g串聯組成；是鎖相環(phase locked loop，PLL)輸出角度；H()是電流調節器傳遞函數；K是軸交叉解耦系數，K=w1f。由于直流電壓環與功率外環控制帶寬遠低于所研究的振蕩頻率范圍，因此可以忽略直流電壓與功率控制回路對阻抗模型的影響，直流電壓dc簡化為固定值，忽略電壓前饋對風電機組輸出阻抗模型的影響。

已有較多研究者采用諧波線性化的方法建立風電機組輸出正負序阻抗模型和電網等值序阻抗模型[17]，在實際工程應用中往往無法掌握風電機組內部詳細的控制策略和控制參數，只能通過頻率掃描的方法實測機端阻抗特性，本文針對圖1所示風電機組的PSCAD/EMTDC模型掃頻實測得到風電機組正負序阻抗特性，如圖2所示。

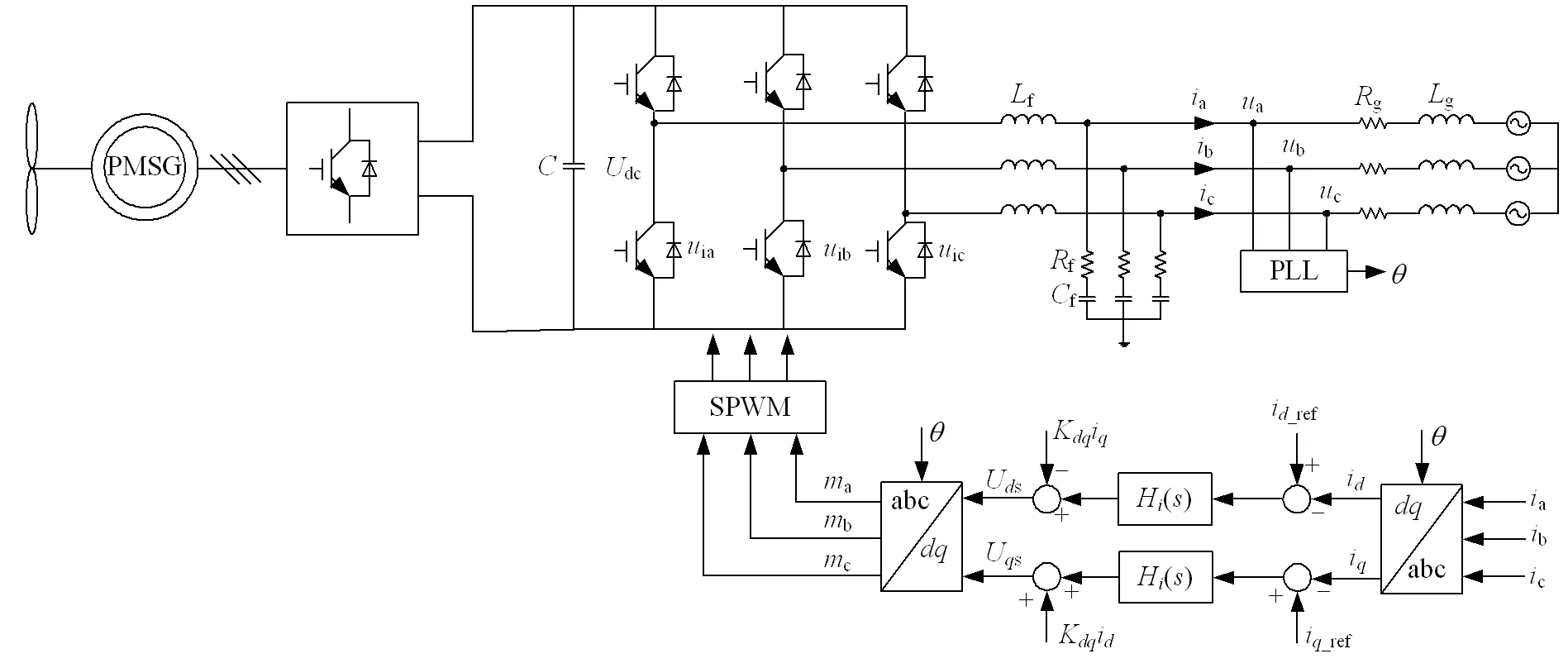
圖1 直驅風電機組并網系統電路結構及控制示意圖

圖2 風電機組輸出正負序阻抗?頻率曲線

1.2 電網序阻抗建模

電網阻抗常用電阻和電感串聯的形式進行等值，其序阻抗模型如下：

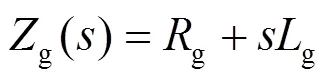
直驅風電機組運行控制參數設置為直驅風電機組典型控制參數[14]。

2 現有基于序阻抗模型的穩定判據分析

2.1 基于阻抗特性的Nyquist判據

利用諾頓等效原則，可以將直驅風電機組并網系統等效為由理想電流源、風電機組輸出阻抗s和電網輸入阻抗g組成的小信號電路模型[17]，如圖3所示。圖3中各電氣量之間的等式關系為

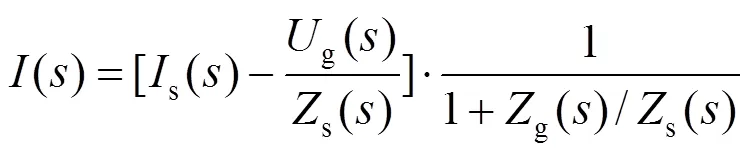
式中：I為風電機組并網點電流；Is為風電機組等效電流源電流；Ug為電網等效電壓源電壓。

為了便于分析直驅風電機組與電網間的交互穩定問題，假定風電機組與電網在互聯之前是各自穩定的，因此()是否穩定取決于式(3)所示函數是否穩定。

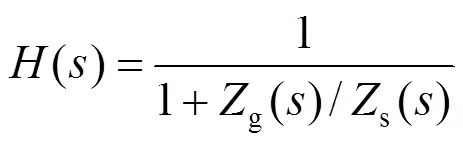
顯然，()是一個閉環傳遞函數，依據線性控制理論，()穩定的前提是g()/s()滿足Nyquist穩定判據。

Nyquist穩定判據能夠很好地判定系統的絕對穩定性(穩定或不穩定)，并通過增益裕量g和相位裕量來衡量系統的相對穩定性，因此在工程中獲得了廣泛應用。但基于阻抗特性的Nyquist穩定判據在確定系統振蕩頻率和評價系統穩定程度方面仍有不足之處。

可通過開環傳遞函數g()/s()的奈氏曲線與單位圓在復平面的交點來確定系統振蕩頻率。這種計算系統振蕩頻率的方法在系統處于臨界穩定狀態時是完全準確的，此時g()/s()的奈氏曲線恰好經過點(-1，0)，奈氏曲線與單位圓的交點即為(-1，0)，此時，該點所對應的頻率即為系統臨界振蕩頻率。

然而，實際系統在大多數情況下往往處于穩定/不穩定狀態，此時g()/s()的奈氏曲線與單位圓在復平面的交點所對應的頻率就不再是系統的實際振蕩頻率，所以此方式僅適用于系統臨界穩定狀態。

Nyquist穩定判據通過增益裕量g和相位裕量可以衡量系統的相對穩定性，但二者之間并不是簡單的比例關系，根據Nyquist曲線的增益裕量和相位裕量不足以對比判斷系統在不同工況下的相對穩定程度。

但是Nyquist判據在實際工程應用中仍具有一定的優勢。實際工程中風電機組控制策略及參數往往是未知的，而采用實驗測得風電機組阻抗s()與電網阻抗g()，通過g()/s()的奈氏曲線在復平面上與單位圓的交點便可以近似地判斷系統振蕩頻率。由于風電機組和電網的實測阻抗與實際阻抗往往存在著一定的誤差，并且實際工程應用對系統振蕩頻率精確度的要求較低，所以基于阻抗特性的Nyquist判據在處理風電機組實測阻抗上具有一定的優勢。

2.2 基于阻抗?頻率特性曲線的波特圖判據

基于風電機組阻抗和電網阻抗頻率特性曲線的波特圖判據與Nyquist判據的基本原理相似。通過解析法或者實測法獲得風電機組和電網的阻抗-頻率波特圖，通過分析風電機組阻抗幅頻曲線與電網阻抗幅頻曲線交點頻率對應的二者相位差D判斷系統穩定性，若D<180°，則系統穩定；反之，則系統不穩定。

波特圖判據不僅能夠定性地判斷系統穩定性，還能通過阻抗?相頻曲線找出系統可能發生的振蕩區域，如圖4所示，這也是波特圖判據相較于Nyquist判據的優勢所在。然而，在定量判斷系統振蕩頻率和比較不同系統穩定程度上，波特圖判據仍存在不足之處。

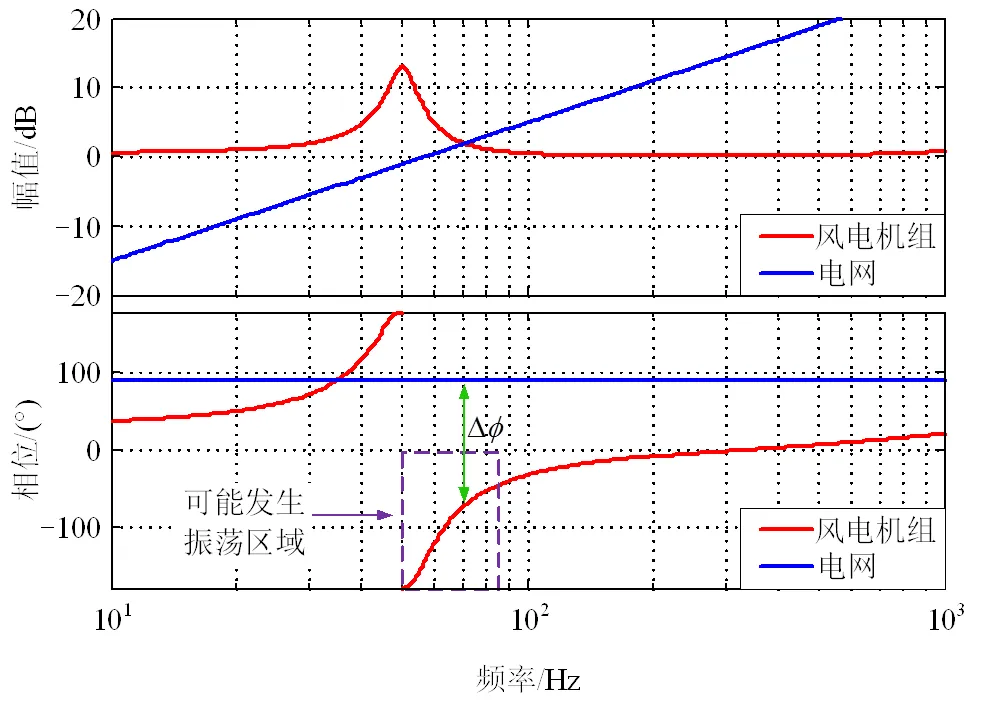
圖4 風電機組并網系統阻抗-頻率波特圖

3 基于擬合分式多項式函數的量化穩定判據

3.1 基于分式多項式函數擬合阻抗特性基本 原理

直驅風電機組并網系統的穩定性取決于式(3)所示的閉環傳遞函數的穩定性，除了Nyquist穩定判據之外，通過求解系統總阻抗total()=s()+g()的零點也可以判斷系統的穩定性[19]。系統總阻抗total()的零點反映了系統阻尼水平和振蕩頻率，定量反映了系統的穩定特性，零點實部決定了系統的阻尼水平，虛部決定了系統的振蕩頻率。相比于Nyquist穩定判據，該方式通過比較不同工況下系統阻尼的大小來定量判斷風電機組并網的相對穩定程度，正/負阻尼越大，系統越穩定/不穩定，并且所求零點的虛部直接決定了系統的振蕩頻率。

通過對直驅風電機組并網系統的阻抗建模，獲得了直驅風電機組輸出阻抗s()和電網輸入阻抗g()的頻域解析表達式，代入total()求解零點，可以計算得到系統振蕩模式的頻率和阻尼。然而，實際系統往往包含多個動態元件，系統的階數非常高，得到的total()解析表達式很復雜，直接求解total()零點非常困難；或者在實際工程中因無法得到風電機組內部準確的控制策略和控制參數，而無法理論推導得出阻抗特性解析表達式，只能通過掃頻的辦法實測出端口阻抗特性曲線。針對以上2種情況都需要研究如何利用total()來量化分析系統穩定性。

函數擬合是對已獲得實驗數據曲線進行分析的重要數學方法。根據函數擬合的基本原理，可以采用形如式(4)的分式多項式對直驅風電機組并網系統阻抗曲線在一頻段內進行擬合。

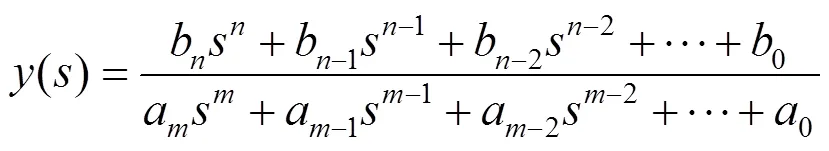
式中b，b?1，…，0，a，a?1，…，0，，均為實常數。

在一段頻帶范圍內利用式(4)對total()進行擬合，在獲得較高擬合精度的前提下，擬合區間內應有()=total()成立。如果total()在擬合區間內存在零點，則該零點也存在于擬合多項式()中，反之亦成立。因此，在擬合精度很高(即擬合誤差很小)時，擬合分式多項式能夠準確反映擬合區間內total()的所有零點。在得到擬合分式多項式函數的基礎上，就可以對系統穩定特性進行量化分析。

3.2 擬合分式多項式函數的選擇原則

對于任一形如式(4)的分式多項式函數，并非均能滿足擬合的要求。

1）=1，取任意值。

此時，分子多項式可以表示為1()=0+1，對擬合后的分式多項式求解零點，即求解1()=0的根，由于表達式中系數均為實數，1()不存在復數零點，如此便不能反映出原函數total()存在復數共軛根的情形，所以此類多項式不能滿足擬合的要求。

2）=2，=0。

此時由于=0，原分式多項式就可以轉化為普通多項式表示，即

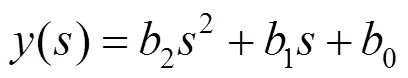
將=j代入式(5)中，可得

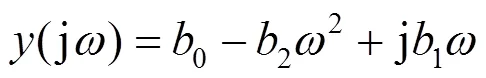
式中=2p，其中是頻率。

不難看出，式(6)中擬合多項式的實部是關于頻率的非線性函數；虛部是關于頻率的線性函數。由于阻抗實部-頻率、虛部-頻率曲線往往是非線性曲線，采用此類多項式在實際擬合中很難保證在擬合區間內有很小的擬合誤差，因此，此類多項式不能滿足擬合的要求。

3）=2，=1。

此時擬合多項式形式為

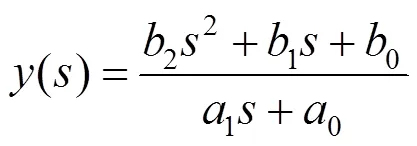
將j代入式(7)中，可得

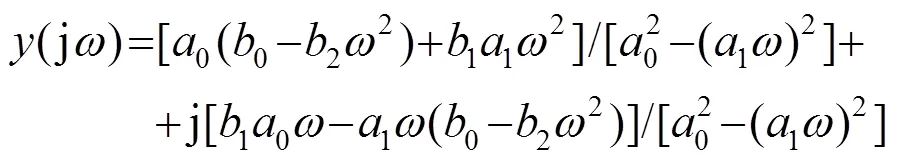
顯然，此類多項式的實部與虛部均為頻率的非線性函數，因此，此類多項式可以在一個區間內對total()進行擬合。

特別地，若令0=0，式(8)可轉化為如下形式：

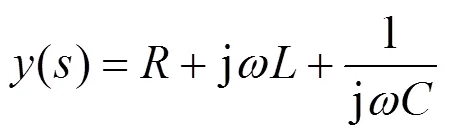
式中：=1/1；=2/1；=1/0。

式(9)中擬合多項式的實部是一常數，虛部是關于頻率的非線性函數。由于阻抗實部-頻率曲線往往是非線性曲線，所以此類多項式不能滿足擬合的要求。

因此，為了獲得更高的擬合精度，形如式(4)的多項式應當滿足分子多項式階數32，分母多項式階數31。

3.3 擬合分式多項式函數的精度分析及穩定判據實現

擬合分式多項式函數曲線擬合的精度可以利用擬合優度2來衡量：

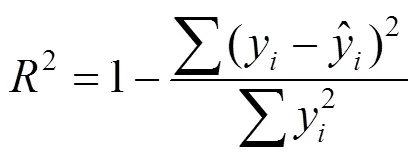
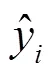
定義擬合誤差與擬合優度2有如下關系：

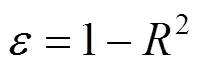
為了簡化分析過程，采用形如式(4)的多項式對系統總阻抗特性曲線total()進行擬合。以網側連接電阻值g=0W，電感值g=2.8mH工況為例，擬合頻率區間選擇(60，80)Hz，擬合分式多項式分子階數、分母階數取值較小會產生較大的擬合誤差，隨著、取值的增大，擬合誤差減小，擬合的精度提高。

擬合頻率區間選擇(60，80)Hz，不同的擬合分式多項式階數對擬合結果的影響如表1所示。結果表明，在擬合誤差很小時，擬合多項式階數對系統穩定性量化分析的結果影響很小。

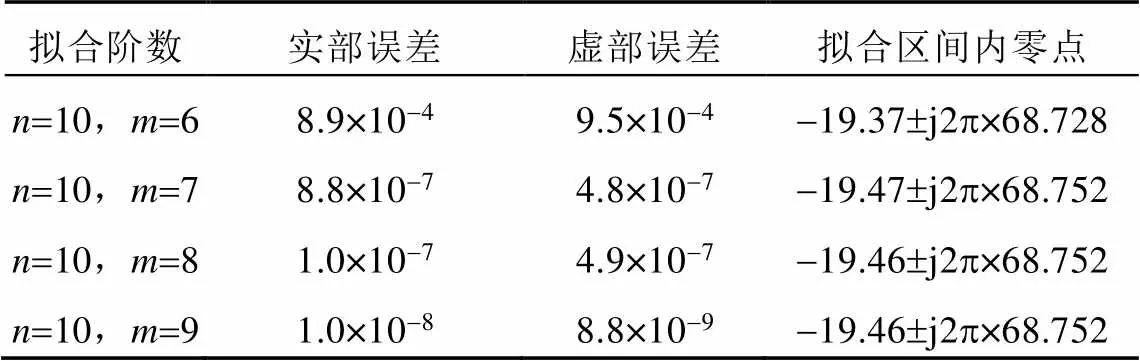
表1 擬合多項式階數對擬合結果的影響

通過對比分析表1數據不難看出，在保證較高擬合精度的前提下，擬合階數、的選取對系統穩定性量化分析結果影響很小。

以網側電阻值g=0W，電感值g=2.8mH工況為例，擬合頻率區間選擇(60，80)Hz，不妨取=10，=8。通過式(10)、(11)可計算得到阻抗實部擬合誤差為1.0×10-7，阻抗虛部擬合誤差為4.9×10-7，擬合分式多項式在(60，80)Hz范圍內的零點為?19.46±j2p×68.752。因此，根據穩定 判據原理可知系統在該工況下的振蕩頻率為68.752Hz，阻尼為?19.46s-1，系統SSO穩定。

4 算例驗證與分析

直驅風電機組接入電網的強弱常用連接的電抗值來表征，連接電抗值越小，電網強度越高。表2為電網連接電感值變化時，通過擬合分式多項式、Nyquist穩定判據2種方式求得的系統振蕩頻率和阻尼。衡量穩定性指標為阻尼值，即零點的實部，正阻尼為穩定，負阻尼為不穩定，絕對值越大，程度越深。分析結果表明，隨著電網連接電感值的增大，系統振蕩頻率降低，阻尼減弱，系統發生不穩定SSO風險升高。

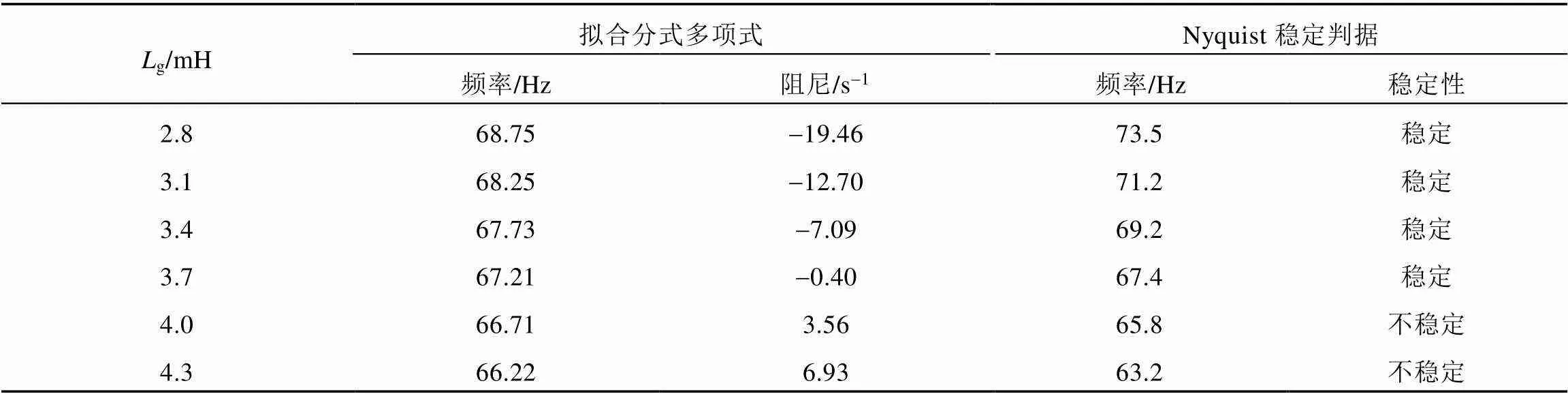
表2 擬合分式多項式、Nyquist穩定判據計算結果對比

在PSCAD/EMTDC仿真平臺中搭建直驅風電機組接入交流電網的時域仿真模型。在仿真中設置1s時系統中加入一個擾動，改變電網側的連接電抗值，得到風電機組輸出的有功功率波形如圖5所示。對風電機組并網點電流進行傅里葉分析，得到系統振蕩頻率如表3所示。

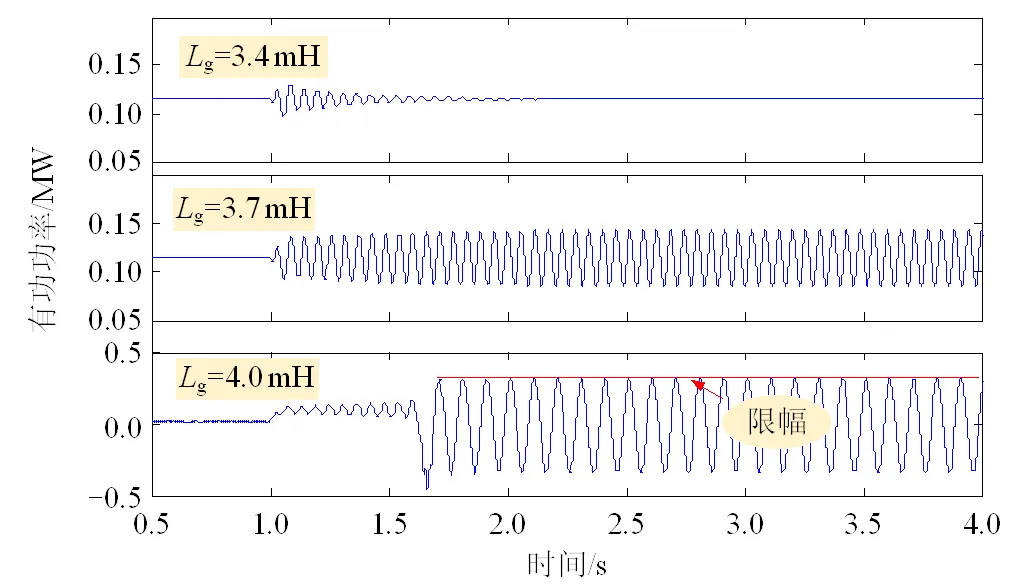
圖5 直驅風電機組有功功率輸出波形

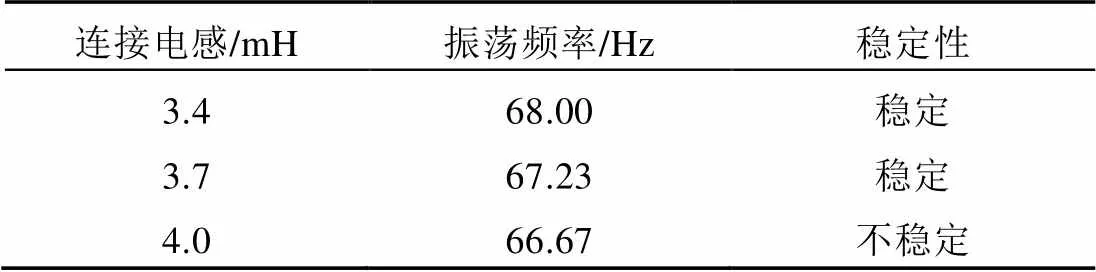
表3 連接電抗對系統SSO特性的影響

仿真結果表明：隨著網側連接電感值的增大，系統的振蕩頻率降低，系統發生不穩定SSO的風險升高。由此可見，通過多項式擬合穩定判據獲得的量化指標能很好地反映系統的穩定性特征。

5 結論

提出了一種采用分式多項式函數擬合風電機組機并網系統總阻抗的方法，通過求取擬合多項式零點獲得系統振蕩頻率及阻尼，從而實現了風電機組并網穩定性的量化分析。所得結論如下：

1）基于阻抗特性的Nyquist穩定判據中，通過奈氏曲線在復平面上與單位圓的交點來判斷系統振蕩頻率的方式僅適用于系統臨界穩定狀態；通過相位裕量和增益裕量來衡量不同系統間相對穩定程度時仍存在不足之處。

2）采用分式多項式函數擬合理論推導或實測的系統阻抗?頻率曲線，在擬合頻段內分式多項式與原阻抗特性等價。基于分式多項式的零點定量判斷系統的振蕩頻率和阻尼水平，彌補了以往阻抗穩定判據的不足。通過比較系統阻尼大小實現不同系統間相對穩定程度的對比，拓展了量化穩定判據的適用范圍，系統正/負阻尼很大時，分式多項式擬合判據仍具有較高的精度。

3）為了獲得較好的擬合精度，擬合的分式多項式應當滿足分子多項式階數32，分母多項式階數31。擬合區間相同時，擬合多項式階數越高，擬合誤差越小。滿足一定擬合階數后，若再增加階數，對所求零點的誤差影響很小。

[1] 田軍，張聞一，王玉鵬，等．風電并網系統次同步振蕩建模與分析[J]．分布式能源，2018，3(5)：22-27．

Tian J，Zhang W Y，Wang Y P，et al．Modeling and analysis of sub-synchronous oscillation in wind power grid connection system[J]．Distributed Energy，2018，3(5)：22-27．

[2] 方力，潘學萍，鞠平．SVC對雙饋風電場次同步振蕩影響及抑制策略[J]．廣東電力，2019，32(3)：52-58．

Fang L，Pan X P，Ju P．Impact of SVC on sub-synchronous oscillation of DFIG-based wind farms and suppression strategy[J]．Guangdong Electric Power，2019，32(3)：52-58．

[3] 袁華，陳景召．聯合模糊聚類和多樣本SSO優化SVR的配電通信網絡流量預測[J]．電網與清潔能源，2018，34(5)：36-43．

Yuan H，Chen J Z．Prediction method based on FCM and multi-sample social spider optimization SVR for distribution communication network traffic[J]．Power System and Clean Energy，2018，34(5)：36-43．

[4] 王一珺，杜文娟，陳晨，等．基于復轉矩系數法研究并網雙饋風電場引發電力系統次同步振蕩問題綜述[J]．發電技術，2018，39(3)：195-203．

Wang Y J，Du W J，Chen C，et al．A review of investigations on sub-synchronous oscillations in power systems caused by DFIG wind farms based on the complex torque coefficients method[J]．Power Generation Technology，2018，39(3)：195-203．

[5] 于笑，陳武暉．風力發電并網系統次同步振蕩研究[J]．發電技術，2018，39(4)：304-312．

Yu X，Chen W H．Review of subsynchronous oscillation induced by wind power generation integrated system[J]．Power Generation Technology，2018，39(4)：304-312．

[6] 邱衍江，張新燕，張超，等．新能源匯集地區廣域次同步振蕩監測系統研究與構建[J]．電力系統保護與控制，2019，47(1)：88-94．

Qiu Y J，Zhang X Y，Zhao C，et al．Research and construction of wide-area subsynchronous oscillation monitoring system in new energy influx area[J]．Power System Protection and Control，2019，47(1)：88-94．

[7] 董曉亮，謝小榮，楊煜，等．雙饋風機串補輸電系統次同步諧振影響因素及穩定區域分析[J]．電網技術，2015，39(1)：189-193．

Dong X L，Xie X R，Yang Y，et al．Impacting factors and stable area analysis of subsynchronous resonance in DFIG based wind farms connected to series- compensated power system[J]．Power System Technology，2015，39(1)：189-193．

[8] 畢天姝，李景一．基于聚合短路比的大型風場次同步振蕩風險初篩[J]．電力系統保護與控制，2019，47(5)：52-59．

Bi T S，Li J Y．Risk screening of SSO induced in large-scale wind farms based on aggregated short circuit ratio[J]．Power System Protection and Control，2019，47(5)：52-59．

[9] Sun J．Small-signal methods for AC distributed power systems：a review[J]．IEEE Transaction on Power Electronics，2009，24(11)：2545-2554．

[10] Wen B，Boroyevich D，Burgos R，et al．Small-signal stability analysis of three-phase AC systems in the presence of constant power loads based on measured-frame impedances[J]．IEEE Transactions on Power Electronics，2015，30(10)：5952-5963．

[11] Wen B，Dong D，Boroyevich D，et al．Impedance-based analysis of grid-synchronization stability for three- phase paralleled converters[J]．IEEE Transactions on Power Electronics，2015，31(1)：26-38．

[12] 桑順，高寧，蔡旭，等．功率?電壓控制型并網逆變器及其弱電網適應性研究[J]．中國電機工程學報，2017，37(8)：2339-2350．

Sang S，Gao N，Cai X，et al．A power-voltage controlled grid-connected inverter and its adaptability research under weak grid conditions[J]．Proceedings of the CSEE，2017，37(8)：2339-2350．

[13] 劉青，王金星．大電網新能源系統的數學建模和功率控制策略[J]．電力科學與工程，2017，33(7)：1-8．

Liu Q，Wang J X．The mathematical modeling and power control strategy of large power grid new energy system[J]．Electric Power Science and Engineering，2017，33(7)：1-8．

[14] 張明遠，肖仕武，田恬，等．基于阻抗靈敏度的直驅風電場并網次同步振蕩影響因素及參數調整分析[J]．電網技術，2018，42(9)：2768-2777．

Zhang M Y，Xiao S W，Tian T，et al．Analysis of SSO influencing factors and parameter adjustment for grid-connected full-converter wind farm based on impedance sensitivity[J]．Power System Technology，2018，42(9)：2768-2777．

[15] Cespedes M，Sun J．Impedance modeling and analysis of grid-connected voltage-source converters[J]．IEEE Transactions on Power Electronics，2013，29(3)：1254-1261．

[16] 辛煥海，李子恒，董煒，等．三相變流器并網系統的廣義阻抗及穩定判據[J]．中國電機工程學報，2017，37(5)：1277-1292．

Xin H H，Li Z H，Dong W，et al．Generalized- impedance and stability criterion for grid-connected converters[J]．Proceedings of the CSEE，2017，37(5)：1277-1292．

[17] Sun J．Impedance-based stability criterion for grid- connected inverters[J]．IEEE Transactions on Power Electronics，2011，26(11)：3075-3078．

[18] 劉方誠，劉進軍，張昊東，等．基于G-范數和sum-范數的三相交流級聯系統穩定性判據[J]．中國電機工程學報，2014，34(24)：4092-4100．

Liu F C，Liu J J，Zhang H D，et al．G-norm and sum-norm based stability criterion for three-phase AC cascade systems[J]．Proceedings of the CSEE，2014，34(24)：4092-4100．

[19] 劉華坤，謝小榮，何國慶，等．新能源發電并網系統的同步參考坐標系阻抗模型及其穩定性判別方法[J]．中國電機工程學報，2017，37(14)：4002-4007．

Liu H K，Xie X R，He G Q，et al．Synchronous reference frame based impedance model and stability criterion for grid-connected renewable energy generation systems[J]．Proceedings of the CSEE，2017，37(14)：4002-4007．

[20] Liu H，Xie X，Zhang C，et al．Quantitative SSR analysis of series-compensated DFIG-based wind farms using aggregated RLC circuit model[J]．IEEE Transactions on Power Systems，2016，32(1)：474-483．

[21] Miao Z．Impedance-model-based SSR analysis for type 3 wind generator and series-compensated network [J]．IEEE Transactions on Energy Conversion，2012，27(4)：984-991．

[22] Liu H，Xie X，Yu L，et al．A small-signal impedance method for analyzing the SSR of series-compensated DFIG-based wind farms[C]//Power & Energy Society General Meeting．Denver，CO，USA：IEEE，2015：1-5．

Stability Criterion of Subsynchronous Oscillation of Direct Drive Permanent Magnet Synchronous Generator Based on Impedance Polynomial Fitting

YU Yongjun1, WANG Lichao1, ZHANG Mingyuan2, XIAO Shiwu2*, ZHANG Xinyuan2

(1.State Grid Xinjiang Electric Power Research Institute, Urumqi 830011, Xinjiang Uygur Autonomous Region, China; 2. School of Electrical & Electronic Engineering, North China Electric Power University, Changping District，Beijing 102206, China)

Impedance analysis is the leading method of solving the stability issues of grid-connected renewable energy generation systems. Taking the grid-connected system of direct drive permanent magnet synchronous generator (D-PMSG) as an example, the characteristics and application scope of the existing Nyquist stability criterion were analyzed. In order to make up for the deficiency of the existing impedance stability criterion, a quantitative stability criterion based on the fitting of fractional polynomial function of impedance characteristic was proposed, which applied port impedance characteristics of wind turbine derived or measured by equivalent fitting theory of fractional polynomial function. Within the fitting frequency band, the fractional polynomial was equivalent to original impedance characteristic. The oscillation frequency and the damping level of the given system were calculated by finding the zero point of fitting polynomial, which could analyze quantitatively the stability characteristics of the system. Finally, the correctness and effectiveness of the fractional polynomial fitting criterion were verified by theoretical analysis and time domain simulation.

direct drive permanent magnet synchronous generator (D-PMSG); sequence impedance characteristic; polynomial fitting; sub/super-synchronous oscillation; stability criterion

10.12096/j.2096-4528.pgt.19140

TM315；TM712

國家重點研發計劃項目(2018YFB0904003)；國網新疆電力公司科技項目(SGXJDK00DJJS 1800169)。

Project Supported by National Key Research and Development Program of China (2018YFB0904003); Science and Technology Project of State Grid Xinjiang Electric Power Company (SGXJDK00DJJS 1800169).

2019-09-23。

(責任編輯 尚彩娟)