梯形加減速算法在MCU控制步進電機中的應用研究

摘要：為了實現單片機對步進電機的精準控制，通過研究梯形加減速運動數學模型分析電機機械運動特性，建立了速度與脈沖、加減速度的數學關系，在STM32單片機中實現了梯形加減速算法的轉換。經調試，步進電機在MCU控制下運行平滑穩定，響應靈敏，不存在失步、過沖現象。

關鍵詞：梯形算法;數學模型;步進電機;MCU

0? ? 引言

隨著企業的轉型升級，智能化設備備受企業青睞，由于步進電機無需反饋就能對位置和速度進行精準控制，故其在工業自動化設備中應用極為廣泛。但在一些速度變化較大、加減速頻繁的設備中，步進電機時常發生失步、過沖等現象，導致控制失靈、精度不高等問題。本文對上述問題進行研究，發現通過梯形加減速算法控制步進電機，具有運行穩定、響應靈敏的優點，不存在失步、過沖等現象。

1? ? MCU控制步進電機硬件系統

如圖1所示，MCU控制步進電機硬件系統以STM32F103單片機為核心，硬件系統包含了四大部分：一是串口觸摸屏，主要用于用戶輸入步進電機運行步數、加速度、減速度、最高運行速度等數據，并提供控制步進電機前進、后退和急停的按鈕;二是步進電機驅動部分，該部分主要由四線制57H2P7842A4步進電機和DM542驅動器組成，用于驅動負載的滾珠絲桿滑臺在直線導軌上按規定的速度穩定、平滑地往返運動;三是復位檢測傳感器，系統啟動時根據傳感器位置信號使滾珠絲桿滑臺復位;四是電源部分，該電源主要為負載提供3.3 V、5 V、24 V直流電壓。

2? ? 梯形加減速運動數學模型

步進電機梯形加減速運動數學模型如圖2所示，模型曲線以角速度ω、時間t分別為縱軸和橫軸，曲線有恒加速、勻速和恒減速三個階段，涉及最高速度SPD、電機運行步數L、加速度A和減速度D四個參數。通過研究模型曲線分析電機角速度ω、加減速度？覣、脈沖信號周期δt、脈沖數n等參數的數學關系，使步進電機在MCU控制下按照梯形曲線做平滑穩定的機械運動，避免發生失步和過沖現象。

2.1? ? MCU定時器值與電機加減速度數學關系

通常，步進電機運轉速度的大小取決于其輸入數字脈沖信號頻率的高低，脈沖頻率越高速度越快，與周期長短的關系則反之。

因此，MCU根據Cn與加減速度、步進電機步距角、脈沖數n以及定時計數器的計數頻率的數學關系自動生成定時計數器的計數值，從而輸出第n步步進電機所需相應頻率的脈沖。

2.2? ? 電機加減速度？覣與脈沖數

從圖2（a）可知，步進電機運動梯形曲線有4個變化階段：一是從零開始加速;二是恒加速到勻速;三是勻速到恒減速;四是減速至停止，如使步進電機按照曲線軌跡運動，除控制好脈沖頻率之外，還要掌握其加減速度變化時刻的規律。

3? ? 算法在MCU中的實現

根據梯形曲線數學模型（圖2），步進電機運動狀態可分為停止、加速、勻速和減速4種狀態，其中開始和停止時刻可統稱為停止狀態。

4? ? 安裝與調試

4.1? ? 硬件安裝

硬件安裝主要包括三大部分，一是串口觸摸屏模塊，二是電機驅動器模塊，三是位置傳感器模塊。

串口觸摸屏通過串行方式與STM32單片機通信，具有編程簡單、操作方便等優點，安裝時只需要接通DC5 V電源和兩機通信線TX、RX即可。步進電機控制系統觸摸屏主控界面主要有步進電機運行總步數、最高速度、加速度、減速度4個輸入參數窗口，其中速度單位為rad/sec，加減速度單位為rad/sec2;界面中還有電機前進、后退和急停3個控制按鈕。

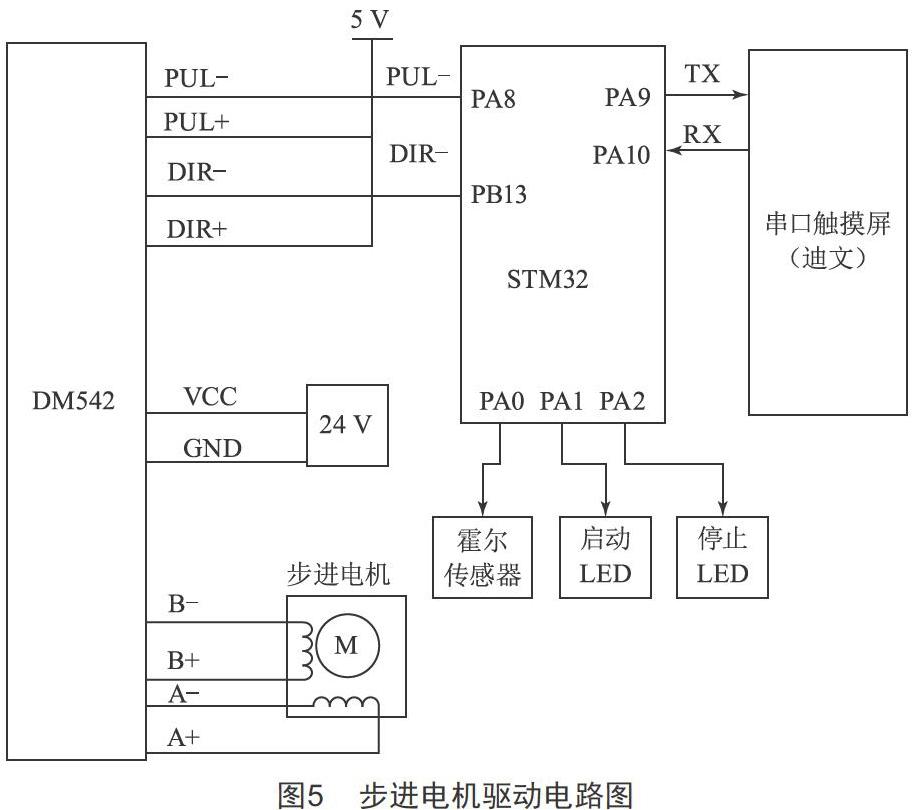
步進電機驅動電路如圖5所示，電機驅動器采用共陽極接法，工作電源為DC24 V，信號端電源為DC5 V，脈沖信號輸入端PUL-和方向控制端DIR-分別接至STM32F103單片機的定時計數器脈沖輸出端PA8和PB13端口。

步進電機復位檢測采用了霍爾傳感器，當MCU系統開機時自動檢測滾珠絲桿滑臺是否在原點，如不在原點則自動復位。調試過程中使滾珠絲桿滑臺偏離原點，開機觀察能否自動復位。

4.2? ? 調試與分析

調試前把電機驅動器的細分數設為32，即6 400步/轉，步進電機電流設置對應為2.8 A，然后在步進電機控制系統主控界面輸入不同的運行步數、最高運行速度、加速度和減速度值，在調試過程中，可借助電機啟動或停止同步狀態指示燈觀察步進電機有無失步、過沖等現象，如依序輸入12 800（6 400×2）、1 200、600、600，點擊“前進”按鈕，同時會觀察到啟動指示燈快速閃爍1次，這時電機將按照設定參數做加減速運動，電機轉動2圈后停止，停止同步狀態指示燈快速閃爍2次。經輸入不同值進行調試，發現步進電機運行過程平滑穩定，沒有發生失步和過沖等現象，梯形加減速算法在MCU控制步進電機中起到了關鍵作用。

5? ? 結語

用戶給定運行步數、最高運行速度和加減速度的前提下，在MCU控制步進電機中植入梯形加減速算法后，經測試，步進電機運行平滑穩定、響應靈敏，避免了在啟動或停止時發生失步或過沖等現象。

[參考文獻]

[1] 湯建文，王仁波，王海濤.基于FPGA的數字多道梯形成形算法研究[J].測試技術學報，2018（5）：405-410.

[2] 肖利哲，王學娟.基于變步長梯形算法GM（1，1）模型背景值的優化[J].統計與決策，2016（23）：8-11.

[3] MADNI A M，VUONG J B，YANG D C H，etal.A Differential Capacitive Torque Sensor With Optimal Kinematic Linearity[J].IEEE Sensors Journal，2007，7（5）：800-807.

[4] 宋玉宏，周定藝，詹金遠，等.基于STM32單片機的電機驅動設計[J].順德職業技術學院學報，2018（2）：6-9.

收稿日期：2020-04-29

作者簡介：劉俊侃（1971—），男，廣東東源人，講師，研究方向：機電一體化。