拋體運動的位移平行四邊形及其應用
葉鈁舟
(樂清市知臨中學 浙江 溫州 325600)
拋體運動及類拋體運動,一般應用運動的分解法來求解比較常見.以重力場中的拋體運動為例,常分解為沿水平方向(勻速直線運動)和豎直方向(勻變速直線運動)兩個分運動;對在斜面上的拋體運動,也有沿斜面方向與垂直于斜面方向平方向進行運動的分解,得到兩個勻變速直線運動,然后建立運動方程,進行求解;在一些特定的問題中,還可將其看成沿初速度方向的勻速直線運動與一個自由落體運動的合成.
對第三種分解方式,在一些特定的問題中,可以形成一種“拋體運動的位移平行四邊形”,使問題的求解變得相對簡潔.
1 一般拋體運動運動的位移平行四邊形


圖1 拋體的位移平行四邊形

2 應用拋體運動的位移平行四邊形解決問題
【例1】(第35屆全國中學生物理競賽預賽第6題)田徑場上某同學將一鉛球以初速度v0拋出,該鉛球拋出點的高度為h,重力加速度大小為g.求:
(1)鉛球在田徑場上的落點與鉛球拋出點的最大水平距離;
(2)對應的拋射角α.


圖2 鉛球運動的位移平行四邊形
過O點作OP⊥B1B,交B1B于P,由圖2可知x=2·OP,則△OBB1的面積為
(1)
而
代入式(1)兩邊,化簡可得
顯然,當α+β=90°時,最大水平距離為
(2)因∠BOB1=90°,故∠OBB1=α,則
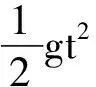
(2)如果在足夠長的斜面上A點以一定大小的初速度拋出一個小球,設落點最遠在斜面上B點,過B作一水平線(看成一個水平地面),則當從A拋出小球落至該水平地面上,水平距離最遠的必在B點.這就說明“斜面上拋射落點最遠”與“鉛球落點最遠”兩個問題,都有初、末速度方向垂直的條件.
【例2】如圖3所示,一斜面體ABC兩斜面傾角分別為θ和φ,底邊AC水平,一質點從傾角為θ的斜面底角處做斜上拋運動.求為使質點從斜面體的頂角處切過,并恰好落在傾角為φ的斜面底角處,則質點的拋射角α與傾角θ,φ應滿足什么關系?(用簡單形式寫出)

圖3 質點斜拋經過A,B,C
解析:如圖4所示,同時作出質點從拋出點A到頂角處B的位移平行四邊形及由B到另一底角處C的位移平行四邊形,過B點作水平線交AE于H,交CF的延長線于K,設B到底邊AC的高度為h,AM=x1,CM=x2.

圖4 兩個相關聯的位移平行四邊形
由圖可知,從A運動到B,有
(1)
(2)
由式(1)和式(2)化簡可得
2tanθ=tanα-tanβ
(3)
從B到C,由拋物線對稱性,易知過C處的速度方向也與水平方向成α角,且∠KBF=β,類似的有

(4)
(5)
由式(4)、(5)得
2tanφ=tanα+tanβ
(6)
由式(3)、(6)可得
tanθ+tanφ=tanα
這就是α,θ,φ應滿足的關系的一種簡單形式表示。
【例3】(全國中學生物理競賽賽題)炮從掩蔽所下向外射擊,掩蔽所與水平面傾斜成角α,如圖5所示,炮位于離掩蔽所的地基(B點)相距l的A點處,炮彈的初速度v0,炮彈飛行的軌道位于圖面上,求炮彈飛行的最遠射程Lm.

圖5 原賽題附圖
解析:設以傾角θ發射炮彈時,軌跡恰好與掩蔽所相切,切點為P,位移平行四邊形如圖6所示.

圖6 A運動到P的位移平行四邊
設A到P運動時間為t,則
A到P與P到A對應的水平分速度相等,即
vx=v0cosθ=v1cosα
(7)
AP對應的水平分位移為
(8)
分析豎直速度變化可求得
(9)
則水平分位移也可表示為
(10)
將式(7)中的兩式分別代入式(10),可得
(11)
由式(8)、(11)可得
(12)
得
討論:當θ=45°時(對應的α記為α0),式(12)可化為
兩邊平方化簡得
也就是說:
(1)當α≥α0時,必能以傾角θ=45°方式發射炮彈,最遠射程為
(2)當α<α0時
3 結論與思考
拋體運動問題在涉及速度方向(如對應于拋射角問題)的討論中,應用位移平行四邊形輔助進行分析,提供了拋體運動的一種全新的幾何視角,并可將問題適當簡化,比如將“鉛球最遠射程”和“斜面上拋體的最遠射程”兩種問題,統一到“初、末速度相互垂直”的相同條件上,甚至對于某些“拋體的最小速度”問題,也可統一到這個條件上來.
拋體運動的位移平行四邊形在數學上與“拋物線的阿基米德三角形”有一定的聯系,比如“拋物線的焦點弦兩端點切線相互垂直”就與“斜面上拋體的最遠射程對應初末速度相互垂直條件”相對應,因此,拋體的位移平行四邊形對數學中拋物線性質的研究,也會有一定的輔助作用,這充分體現了數學與物理之間相互融合的關系.

