深基坑開挖變形監(jiān)測及數(shù)值計(jì)算分析
柴海博
(中鐵十七局集團(tuán)有限公司 山西太原 030006)
1 引言
欒長青[3]以上海軌道交通9號(hào)線宜山路車站降水施工為依托,在現(xiàn)場降水試驗(yàn)的基礎(chǔ)上,結(jié)合高壓固結(jié)試驗(yàn)和Plaxis 3D Foundation軟件研究了基坑降水開挖對(duì)周邊土體工程性狀的影響。程子龍[4]以太原地鐵2號(hào)線中心街站為研究對(duì)象,通過野外抽水試驗(yàn)及室內(nèi)土工試驗(yàn)獲取了各地層參數(shù)及滲透性,并運(yùn)用FLAC3D分析了不同工況下地層的水平位移與地表的沉降。游洋[5]等將基坑分區(qū)進(jìn)行降水設(shè)計(jì)來研究對(duì)周邊環(huán)境的影響,制定不同的方案并采用數(shù)值計(jì)算方法驗(yàn)證了方案的可行性。吳薪柳[6]采用數(shù)值計(jì)算評(píng)估了復(fù)雜基坑開挖對(duì)既有地鐵結(jié)構(gòu)安全性的影響。結(jié)果顯示,隨著基坑降水開挖的進(jìn)行,坑底土體會(huì)出現(xiàn)回彈,在坑外地表出現(xiàn)沉降。邱玉[7]等在比較現(xiàn)場實(shí)測值和分析計(jì)算結(jié)果的基礎(chǔ)上,提出了坑周土體沉降是由基坑降水后土體應(yīng)力重分布所導(dǎo)致。黃顯貴[8]等通過數(shù)值計(jì)算和現(xiàn)場實(shí)測數(shù)據(jù)驗(yàn)證了地表沉降的理論計(jì)算方法。方浩[9]等通過研究指出了圍護(hù)墻最大側(cè)向位移發(fā)生位置和地表沉降影響范圍。唐洪亮[10]等通過模型試驗(yàn)和數(shù)值模擬,探討了膨脹土地層開挖過程中基坑變形規(guī)律。吳昌將[11]等以現(xiàn)場實(shí)測數(shù)據(jù)研究了軟土地區(qū)基坑變形性狀及對(duì)周邊建筑的影響。楊果林[12]等借助現(xiàn)場監(jiān)測和數(shù)值模擬,研究了滲流-應(yīng)力耦合條件下泥炭土深基坑的開挖變形規(guī)律。靳國柱[13]通過現(xiàn)場監(jiān)測總結(jié)分析了軟土地區(qū)地鐵車站深基坑開挖一般受力變形規(guī)律。孫超[14]等通過理論計(jì)算與實(shí)際監(jiān)測結(jié)果的對(duì)比,探究了基坑圍護(hù)結(jié)構(gòu)和周邊建筑物等的變形規(guī)律。
本文根據(jù)某地鐵車站深基坑工程開挖時(shí)的現(xiàn)場監(jiān)測數(shù)據(jù),并結(jié)合數(shù)值計(jì)算,對(duì)深基坑變形問題進(jìn)行深入研究,總結(jié)了各監(jiān)測項(xiàng)目的變形發(fā)展規(guī)律。
2 工程概況及地質(zhì)條件
(1)工程概況
擬建車站開挖基坑長239 m,寬20.6~34.8 m,深度16.85~18.4 m,采用800 mm厚、39 m深的地下連續(xù)墻作為主體圍護(hù)結(jié)構(gòu),共設(shè)5道內(nèi)支撐,基坑中部設(shè)置φ1 000立柱樁11根。基坑支護(hù)結(jié)構(gòu)具體形式如圖1所示。

圖1 基坑支護(hù)結(jié)構(gòu)橫剖面(單位:mm)
(2)工程地質(zhì)條件
根據(jù)勘察資料,開挖范圍內(nèi)主要為含水量高、滲透性好的粉土和砂性土。
各主要土層分布及物理力學(xué)特性指標(biāo)見表1。

表1 土的物理力學(xué)性能指標(biāo)
3 基坑監(jiān)測
3.1 監(jiān)測內(nèi)容及測點(diǎn)布置
本工程所涉及的監(jiān)測項(xiàng)目眾多,本文僅選取立柱樁沉降、圍護(hù)墻體深層水平位移和周邊地表沉降作為研究對(duì)象,其監(jiān)測點(diǎn)布置具體情況見表2。
2)要素描述修改的有29個(gè) :大地原點(diǎn)、三角點(diǎn)、衛(wèi)星定位等級(jí)點(diǎn)、地面河流、運(yùn)河、倒虹吸、海島、制水壩、單幢房屋、普通房屋—建筑中房屋、架空房、廊房、管道井(油、氣)、北回歸線標(biāo)志塔、清真寺、衛(wèi)星地面站、柵欄、籬笆、地鐵、輕軌、引道、路標(biāo)、里程碑、火車渡、汽車渡、人渡、泥石流、熔巖流、岸壟、鹽堿地。

表2 監(jiān)測工作布置
3.2 監(jiān)測項(xiàng)目控制值
監(jiān)控項(xiàng)目控制指標(biāo)一般由累計(jì)變化值和變化速率兩個(gè)量控制。根據(jù)圍護(hù)設(shè)計(jì)說明,本工程監(jiān)測控制值見表3。

表3 監(jiān)測項(xiàng)目控制值
3.3 監(jiān)測數(shù)據(jù)分析
(1)立柱樁沉降
隨著基坑開挖卸荷,坑下土體會(huì)產(chǎn)生一定回彈量,土體變形較難監(jiān)測,故通過監(jiān)測基坑內(nèi)立柱樁的隆沉情況來實(shí)現(xiàn)。由圖2可知,隨著基坑開挖,立柱樁沉降會(huì)逐漸增大,且在第四道支撐施工前其增速較快,保持較陡的直線型,累計(jì)變形量達(dá)到設(shè)計(jì)控制值的50% ~60%;此后,變化幅度趨緩,在底板澆筑時(shí)立柱樁沉降值基本達(dá)到峰值,為17~19 mm,均未超過其設(shè)計(jì)控制值25 mm的80%,說明底板澆筑很好地抑制了基底隆起的發(fā)展趨勢。另外,通過圖2中3根立柱樁Lz9、Lz10、Lz11沉降量可以看出,基坑內(nèi)各立柱樁的沉降量差異不大,說明基坑開挖過程各段均為對(duì)稱均勻卸載,滿足設(shè)計(jì)及施工要求。
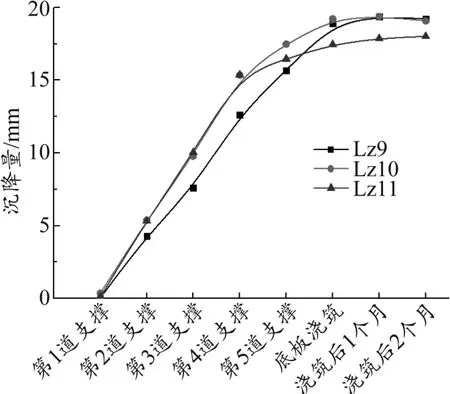
圖2 立柱樁沉降-開挖時(shí)間關(guān)系曲線
(2)墻體深層水平位移
由圖3可知,坑內(nèi)卸載會(huì)導(dǎo)致地連墻在基坑外側(cè)土壓力作用下發(fā)生朝向臨空面的水平位移。由于坑內(nèi)第一道內(nèi)支撐為剛度大、變形小的鋼筋混凝土支撐,其強(qiáng)度的安全、可靠性強(qiáng),能有效限制墻體上部的變形;而墻體下部的入土深度較大,坑下土體產(chǎn)生的側(cè)向土壓力可以減弱墻后主動(dòng)土壓力作用,故墻體的深層水平位移會(huì)沿其深度方向呈先增大后減小的“弓”型曲線,且其最大值總是出現(xiàn)在開挖面附近。另外,隨著基坑開挖,墻體各部位的水平位移會(huì)逐漸增大,直至底板施工后達(dá)到穩(wěn)定,最大值接近50 mm,超過其控制值。位移增長最快的階段為第三層土開挖期間,水平位移最大值增長了約20 mm。主要原因?yàn)樵诨娱_挖過程中,鋼支撐架設(shè)不及時(shí),導(dǎo)致不能形成有效的內(nèi)部支護(hù)結(jié)構(gòu),且存在一定的超挖現(xiàn)象。所以在后續(xù)施工中應(yīng)對(duì)基坑分層、分塊施工,防止超挖,及時(shí)施加內(nèi)支撐。此外,當(dāng)位移變化較大時(shí)應(yīng)加強(qiáng)監(jiān)測。
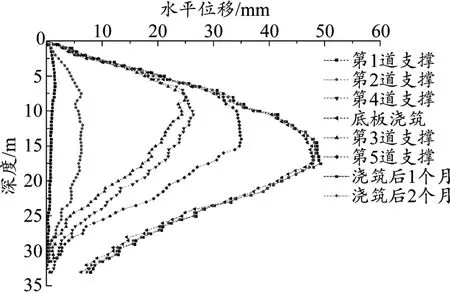
圖3 墻體深層水平位移變化曲線
(3)地表沉降
由圖4可知,基坑卸荷開挖使地連墻發(fā)生朝向坑內(nèi)的水平位移,從而引起周邊地表沉降。隨著開挖的進(jìn)行,沉降量也逐漸增大,直至底板澆筑后趨于穩(wěn)定。最大值8.31 mm為設(shè)計(jì)控制值16.5 mm的50%,說明該基坑支護(hù)形式能有效降低開挖對(duì)周邊環(huán)境的影響。另外,對(duì)比位于同一斷面上的地表沉降監(jiān)測點(diǎn) D11-1、D11-2、D11-3、D11-4,可以看出,隨著監(jiān)測點(diǎn)與基坑距離的增大,其沉降量值在逐漸減小,這也與基坑開挖影響分區(qū)的理論相對(duì)應(yīng);對(duì)比D11-1、D12-1、D13-1,當(dāng)各斷面上的監(jiān)測點(diǎn)與基坑之間距離相同時(shí),其相應(yīng)階段的沉降量值基本一致。
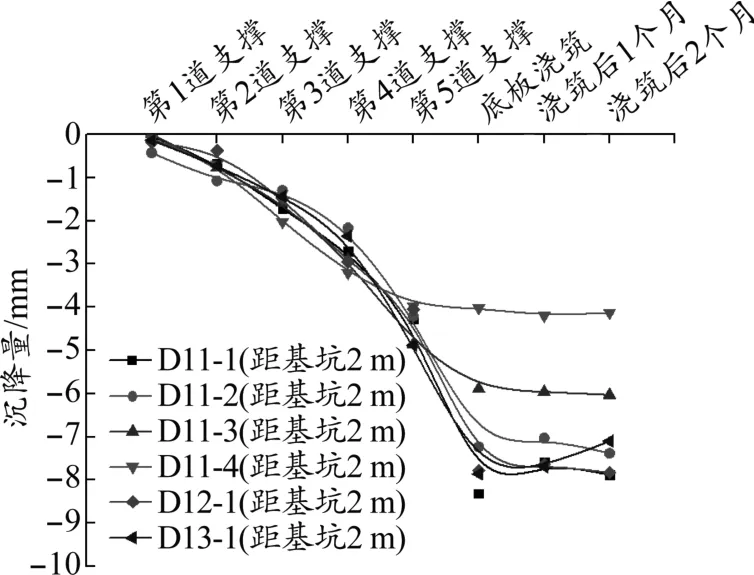
圖4 地表沉降與開挖時(shí)間關(guān)系曲線
4 基坑開挖過程數(shù)值模擬分析
4.1 模型簡介
根據(jù)基坑實(shí)際情況,采用MIDAS建立三維基坑模型,綜合模型的計(jì)算效率及其邊界效應(yīng),尺寸設(shè)置為400 m×184 m×80 m,采用了更加符合實(shí)際的混合網(wǎng)格生成器,并通過析取功能在地連墻外圍設(shè)置了一圈截水帷幕,使模型更貼近于施工實(shí)際。所建立的計(jì)算模型見圖5。
4.2 本構(gòu)模型選取
綜合考慮巖土體材料的非線彈性和塑性,選用修正的摩爾-庫倫彈塑性本構(gòu)。該本構(gòu)模型尤其適用于本工程中砂土類等具有摩擦特性的材料。

圖5 有限元模型
4.3 基坑開挖工況設(shè)置
按照施工順序,可將基坑開挖分為以下7個(gè)階段:
工況一:施工地連墻和立柱樁;
工況二:開挖基坑表層土,施工冠梁和砼支撐;
工況三:降水至第二層土下1 m,挖第二層土,加第二道鋼支撐;
工況四:降水至第三層土下1 m,挖第三層土,加第三道鋼支撐;
工況五:降水至第四層土下1 m,挖第四層土,加第四道鋼支撐;
工況六:降水至第五層土下1 m,挖第五層土,加第五道鋼支撐;
工況七:降水至基坑設(shè)計(jì)開挖深度下1 m,開挖至基坑底部。
4.4 數(shù)值計(jì)算與實(shí)測結(jié)果對(duì)比
(1)立柱樁沉降
如圖6所示,立柱樁沉降的數(shù)值計(jì)算值和現(xiàn)場監(jiān)測值在各施工階段的變化趨勢基本一致,均為前期增長較快,在工況四之后增速減緩,在開挖完成后趨于穩(wěn)定,兩者的終值也較接近。計(jì)算值在施工前期略小于實(shí)測值,主要原因?yàn)樵谀M過程中位于基坑內(nèi)的支撐施加及時(shí),能有效控制基坑變形。數(shù)值計(jì)算的穩(wěn)定終值在19~22 mm,同樣小于設(shè)計(jì)控制值25 mm,表明數(shù)值模擬計(jì)算滿足坑底變形要求。

圖6 立柱樁沉降實(shí)測值與計(jì)算值對(duì)比
(2)墻體深層水平位移
由圖7可知,基坑開挖后,地連墻兩側(cè)呈現(xiàn)對(duì)稱的朝向基坑方向的水平位移,水平位移從上向下表現(xiàn)為先增大后減小的變化趨勢。模擬計(jì)算中墻體深層水平位移在各工況下的發(fā)展趨勢與實(shí)際監(jiān)測值類似,均為隨開挖的進(jìn)行而增大,位移最大值出現(xiàn)的位置也保持在開挖面附近,具體位置見表4。
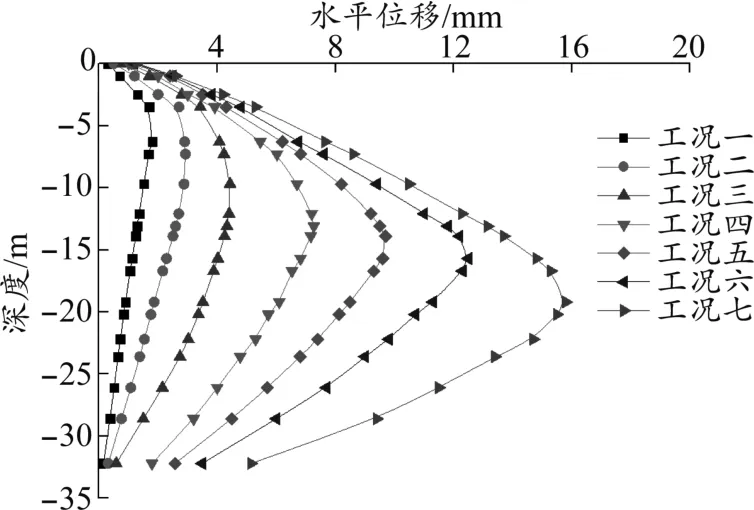
圖7 墻體深層水平位移計(jì)算值
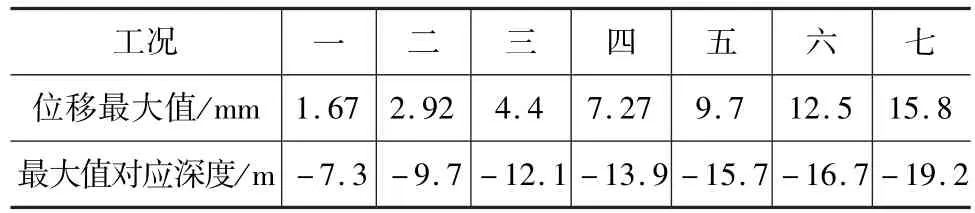
表4 各工況下最大值統(tǒng)計(jì)
對(duì)比圖7和圖3,在各開挖階段,墻體深層水平位移的計(jì)算值均明顯小于實(shí)際監(jiān)測值,且開挖完成后的最大值15.8 mm,明顯小于設(shè)計(jì)控制值23 mm,基坑開挖變形處于可控狀態(tài)。這是因?yàn)樵跀?shù)值模擬中,內(nèi)支撐是在對(duì)應(yīng)土層開挖完成的瞬時(shí)施加上去的,忽略了實(shí)際施工中內(nèi)支撐的施工時(shí)間,減小了基坑處于無支護(hù)狀態(tài)的時(shí)間,是較為理想的施工狀態(tài),故所計(jì)算得到的變形值較小,這也說明在施工中及時(shí)施加內(nèi)支撐可以有效控制地連墻的水平變形。
(3)地表沉降
如圖8所示,地表沉降曲線呈現(xiàn)有規(guī)律的“凹”槽型。隨著基坑開挖,沉降“凹”槽向下發(fā)展,且位移最大值出現(xiàn)的位置會(huì)逐漸遠(yuǎn)離基坑。工況一中,最大沉降為-2.59 mm,距基坑距離為7.2 m;工況七中,最大沉降為-15.28 mm,距基坑邊24 m。基坑開挖完成時(shí),最大沉降值出現(xiàn)的位置小于基坑開挖深度的兩倍,這也符合基坑開挖影響分區(qū)理論。另外,地表沉降最大值-15.28 mm小于設(shè)計(jì)控制值±16.9 mm,表明基坑開挖對(duì)周邊環(huán)境的影響較小。

圖8 地表沉降曲線
5 結(jié)論
通過對(duì)比分析基坑變形的監(jiān)測值和數(shù)值計(jì)算結(jié)果,可以得出以下結(jié)論:
(1)通過坑內(nèi)立柱樁隆起來監(jiān)測坑底土體變形,其監(jiān)測值和計(jì)算值都表現(xiàn)為在工況四之前增長較快,之后增速減緩,在基坑開挖完成時(shí)基本達(dá)到峰值。在各個(gè)階段中,兩者差值不大,且都小于設(shè)計(jì)控制值。
(2)沿墻體深度方向,墻體深層水平位移表現(xiàn)為先增后減的“弓”型曲線。隨著基坑開挖,“弓”型向坑內(nèi)發(fā)展,其最大水平位移出現(xiàn)的位置隨開挖面下移。計(jì)算值較實(shí)際監(jiān)測值更滿足設(shè)計(jì)要求,主要原因?yàn)槟M計(jì)算中內(nèi)支撐施加及時(shí)。
(3)隨著基坑開挖,地表沉降“凹”槽向下發(fā)展,且最大沉降值向遠(yuǎn)離基坑的方向移動(dòng),最終保持在兩倍的基坑開挖深度范圍內(nèi)。

