淺海環境中基于模態衰減規律加權的子空間檢測方法*
孔德智 孫超? 李明楊
1) (西北工業大學航海學院, 西安 710072)
2) (西北工業大學, 海洋聲學信息感知工業和信息化部重點實驗室, 西安 710072)
3) (浙江大學信息與電子工程學院, 杭州 310058)
1 引 言
水下聲源檢測是水聲信號處理所要解決的重要問題之一, 它通過對接收數據進行一定的處理來判斷聲源是否存在. 對于被動聲源檢測, 最優檢測器為匹配模型檢測器(matched model detector,MMD)[1,2]. 在求解MMD 的檢測統計量時, 要求環境參數和聲源位置已知. 然而實際的淺海水聲環境存在不確定性, 聲源位置又是未知的, 因此MMD 并不能實現, 而是作為一般檢測器的性能上限參考.
針對淺海波導環境中的聲源檢測問題, 相關研究人員提出了諸多解決方法. 一類是根據海洋環境和聲源位置的不確定信息建模, 提出MMD 的改進的方法, 如貝葉斯檢測器[2,3](Bayes detector, BD)、基于主成分分析(principle component analysis,PCA)的檢測器[4]和基于蒙特卡羅優化的廣義似然比(Monte Carlo generalized likelihood ratio test,MC-GLRT)檢測器[5]等. BD 利用貝葉斯原理通過對不確定的環境參數和未知的聲源位置進行積分, 最終得到一種平均意義上的最優檢測器, 但它需要復雜的指數和積分運算. 為減小運算復雜度,劉宗偉等相繼提出了PCA 檢測器和MC-GLRT檢測器, 以較低的運算代價實現了性能幾乎接近于BD 的穩健檢測. 這兩種檢測器都需要利用不確定海洋環境中的信號波前采樣與接收數據做匹配相關處理. 當聲源位置可能的區域范圍增大時, 為得到充分的聲場信息, 需要大量信號波前采樣及相應的相關運算, 這將帶來較大的運算負擔. 另一類方法是利用子空間檢測[6]的思想來解決聲源位置未知的問題. 子空間檢測器通過將接收數據能量正交投影到信號子空間來獲得檢測統計量, 應用到水下波導環境時, 不同文獻[7?13]中的命名有所差異,但實際上它們都是同一種檢測器. 由于信號子空間通常由陣列采樣模態信息[14]所張成, 本文中將其稱 為 模 態 空 間 檢 測 器[12](modal space detector,MSD). 受限于陣列孔徑尺寸和環境不確定性,MSD 常會遭遇模態信息非完備采樣和不確定采樣的問題. 對于前者, 文獻[11]通過對模態相關矩陣特征分解給出了一種有效譜檢測器; 而對于后者,文獻[12]利用模態采樣矩陣之間的近似“包含關系”提出了一種穩健檢測方法.
子空間檢測不需要信號波前采樣, 運算量較小且具有較好的穩健性. 對于相同的輸入信噪比(下簡稱信噪比), MSD 的檢測性與模態空間(即信號子空間)維度成負相關, 而波導中的傳播模態數增多將引起模態空間維度增大. 當頻率升高、波導環境深度變大等無可避免的因素造成傳播模態數增多時, 相應MSD 的檢測性能也隨之下降. 這對于水下聲源檢測, 尤其是遠距離傳播的低信噪比聲源檢測十分不利. 為改善MSD 的檢測性能, 文獻[9,10]提出截斷子空間檢測器(truncated subspace detector, TSD), 通過截斷部分傳播模態構造更低維度的信號子空間以提高其檢測性能, 截斷子空間的求取依賴于信噪比; 然而實際中信噪比是未知的, 導致TSD 難以實現. 另外, PCA 檢測器實際上是一種加權子空間檢測器, 其各階主成分分量張成了信號子空間, 但其加權系數與各子空間的信號分量并不匹配, 尤其是當傳播模態數增多時反而會造成檢測器性能的下降.
根據簡正波理論[15], 聲信號以若干階簡正波模態的形式在水下傳播, 傳播過程中伴隨海水吸收、海底反射等過程, 各階簡正波模態系數在傳播過程中會發生不同程度的衰減, 衰減程度與各階模態衰減系數和傳播距離成正相關. 對于遠距離傳播的聲信號, 衰減系數一定程度上反映了各階簡正波模態對聲源信號的貢獻. 因此可考慮利用各階簡正波模態的衰減規律對MSD 進行改進. 本文研究發現, 使 用垂直線列陣(vertical linear array,VLA)時, 利用各階模態函數采樣的近似正交性,可將MSD 分解為若干階獨立的模態子空間檢測器(modal subspace detector, MSSD), 各階MSSD的處理增益與模態系數成正比. 根據模態系數與衰減系數之間的關系設計加權系數, 提出一種加權的模 態 子 空 間 檢 測 器(weighted modal subspace detector, WMSSD). 相同信噪比下, 檢測器的處理增益越大, 其最終的輸出信噪比也越大, 進而其檢測性能也越好. 利用模態衰減規律設計的加權系數反映了各階MSSD 對最終得到檢測器的貢獻, 使WMSSD可獲得高于MSD 的處理增益, 從而WMSSD 可實現更優的檢測性能.
本文所采取的加權方式反映了模態衰減對各階MSSD 處理增益的影響, 而各階MSSD 的處理增益還與聲源位置處模態深度函數[16,17](下簡稱模態函數)的值有關. 聲源位置處模態函數值由聲源位置和模態函數共同決定. 模態函數形狀與相應模態反轉點[17,18]密切相關, 模態反轉點一般位于若干低階模態函數, 其深度由波導中的聲速決定. 因此, 聲源位置和聲速剖面將影響WMSSD 的檢測性能.
本文其他部分安排如下. 第二節推導了淺海環境中的MSD, 給出了其處理增益的計算公式, 并分析了波導環境中傳播模態數對MSD 檢測性能的影響; 第三節給出了本文所提出WMSSD 的推導過程, 并從理論上分析了影響其檢測性能的因素;第四節通過仿真實驗給出了WMSSD 的檢測性能及其相較于MSD 的性能提高效果, 深入探究了聲源位置和聲速剖面對WMSSD 檢測性能的影響,以及導致這種影響的物理機理, 并歸納了WMSSD的適用場景; 第五節給出了本文得出的相關結論.
2 模態空間檢測器
2.1 淺海環境中的聲場模型
考慮淺海波導環境中遠距離窄帶聲源, 假設聲源位置未知、中心頻率f 已知. 根據簡正波理論, 聲源輻射到接收點 (r,z) 處的聲壓傳遞函數可表示為各階簡正波之和的形式
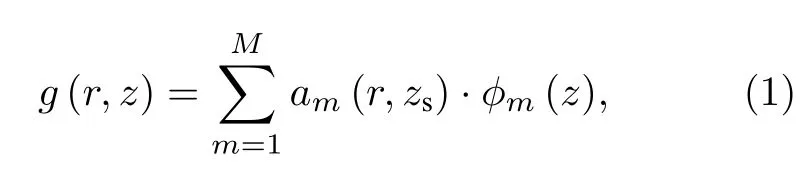
式中,M為波導環境中傳播的簡正波階數,r,zs和z分別為接收點與聲源的水平距離、聲源深度和接收點的深度,?m(·) 為第m階模態深度函數(下簡稱模態函數),am(r,zs) 為第m階模態系數. 模態系數是聲源位置的函數, 其表達式為
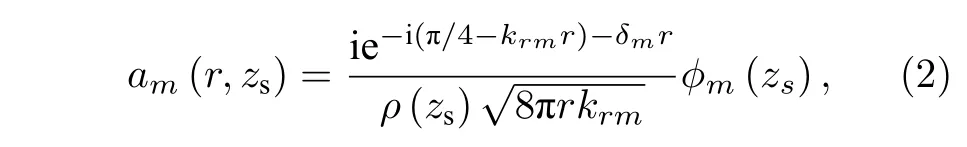
模態系數下文簡寫為am. 模態函數是深度的函數,且滿足正交性
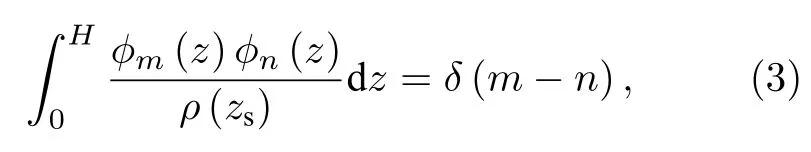
式中,H為波導深度.
利用(1)式, 聲信號傳播到垂直線列陣(vertical linear array, VLA)的傳遞函數可表示為模態矩陣和模態系數向量乘積的形式

式中,N為陣元個數,z1,··· ,zN為各陣元深度,Φ為N ×M維的實矩陣, 記作Φ ∈RN×M, 由各陣元采樣的各階模態函數構成, 下文簡稱模態矩陣;a ∈RM為M維列向量, 由各階簡正波的模態系數構成.
2.2 模態空間檢測器
假設VLA 覆蓋全水深, 且陣元數足夠采集完備的模態信息. 將陣列接收數據變換到頻域進行處理, 可得如下頻域信號檢測模型,
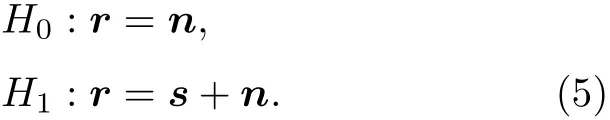

式中,μ為表示聲源幅度和相位的未知復變量. 假設背景噪聲為空間白噪聲, 服從均值為零、協方差矩陣為(IN ∈RN×N為單位矩陣)的多維復高斯分布. (5)式描述了一個二元假設檢驗問題, 零假設H0表示聲源信號不存在, 備選假設H1表示聲源信號存在.
將(4)式和(6)式代入(5)式中, 并記θ=μ·a,則兩種假設下接收數據的概率密度函數分別為[19],
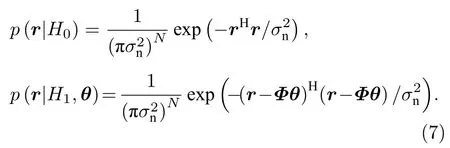
式中, 上標‘H’表示共軛轉置運算. 由于聲源位置未知,θ為未知變量, 進而p(r|H1,θ) 為條件概率密度函數. 令?p(r|H1,θ)/?θ=0, 可得θ的最大似然估計為
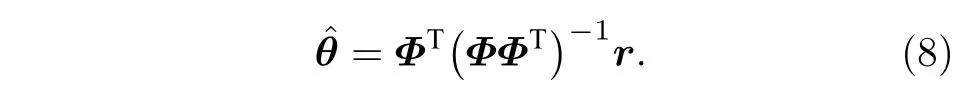
式中, 上標‘T’表示轉置運算. 利用(7)式和(8)式,可得兩種假設下的條件似然比為
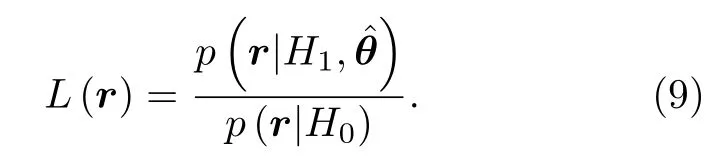
對(9)式做化簡運算并取自然對數, 可得相應的檢測統計量為,
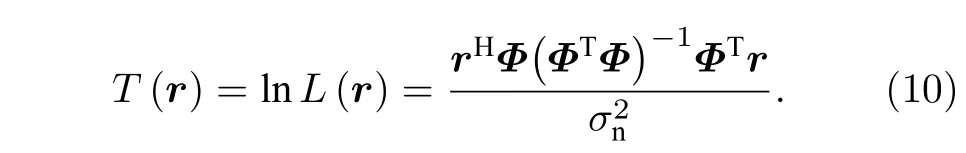
由(10)式可知, 該檢測統計量T(r) (以下簡寫為T)為接收數據在模態矩陣張成空間(以下簡稱模態空間)上的正交投影能量與噪聲功率之比, 因此將該檢測器稱為模態空間檢測器(modal space detector, MSD).
由其檢測統計量可知, MSD 是一種二次型檢測器, 根據統計信號處理的知識[19]可得其服從的統計分布為,
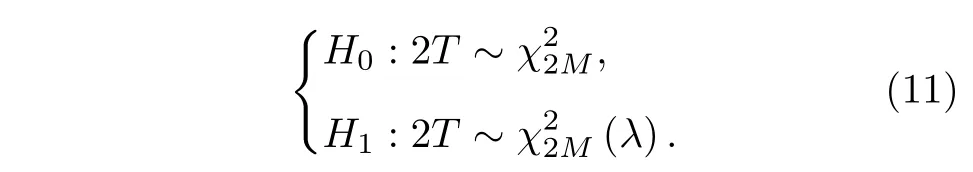

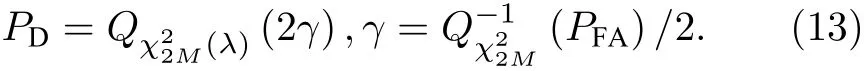
2.3 MSD 的處理增益
使用處理增益來定量地描述檢測器的檢測性能, 其定義為輸出信噪比與輸入信噪比之比,

式中,G為處理增益,OSNR和SNR分別表示輸入信噪比和輸出信噪比. 定義輸入信噪比(下簡稱信噪比)為各陣元接收信號平均能量與陣元噪聲功率的比值,
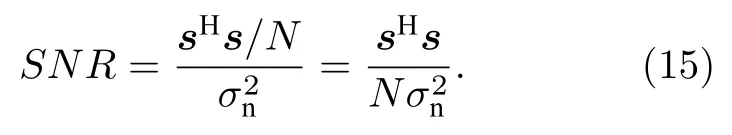
由(12)式和(15)式可知, 非中心參量與信噪比存在關系λ=2N ·SNR. 輸出信噪比可使用檢測器的偏移系數來近似計算[20], 其定義為
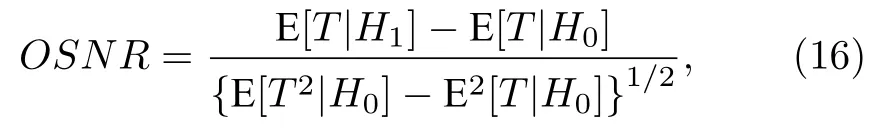
式中, E[·] 表示求期望運算. 利用(15)式和(16)式可得MSD 的處理增益(推導過程見附錄)為

由(17)式可知, MSD 的處理增益與傳播模態階數的平方根成反比, 與陣元個數成正比, 這與2.2 節根據統計分布規律得出的結論一致.
檢測器的處理增益衡量的是檢測器本身對噪聲的抑制能力, 由其表達式也可看出, 它與輸入信噪比無關. 容易理解, MSD 對噪聲的抑制能力隨陣元個數的增多而增強. 而對于相同的信噪比, 當傳播模態數增多時, MSD 將接收數據投影到更高維度的模態空間以獲取所有聲源輻射信號的能量, 但同時也引入了更多維的噪聲分量, 最終導致輸出信噪比減小, 處理增益降低. 因此當聲源頻率增加或波導深度增大而使得波導中傳播的模態數增多時,MSD 的處理增益降低造成檢測性能變差, 這對水下聲源信號檢測尤其是低信噪比的情況極為不利.
3 基于模態衰減系數加權的子空間檢測器
為提高MSD 的處理增益進而改善其檢測性能, 本節先對MSD 做子空間分解, 然后分析各子空間檢測器的處理增益, 并提出一種加權子空間檢測器.
3.1 MSD 的子空間分解
考慮模態深度函數采樣完備的情況, 各階采樣模態向量之間近似滿足正交性, 即為單位矩陣), 將其代入(10)式中可得簡化的檢測統計量,
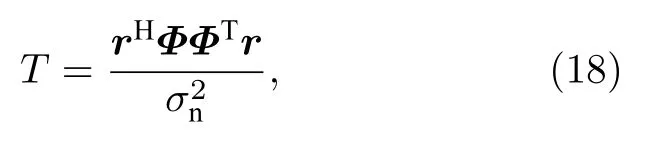
分別記
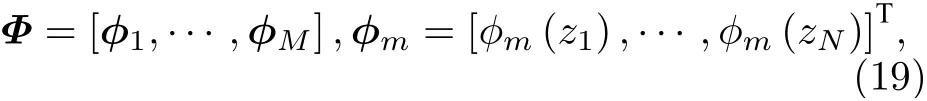
式中,?m為第m階采樣模態函數構成的列向量,則MSD 可寫為M個模態子空間檢測器(mode subspace detector, MSSD)之和的形式,
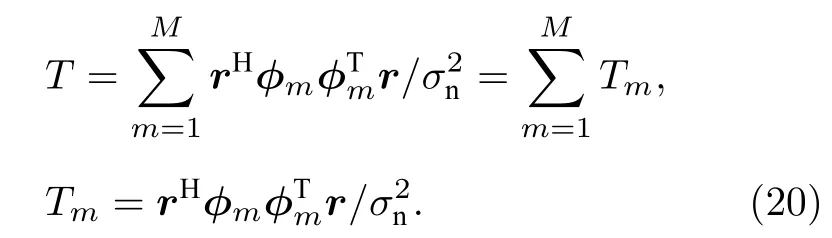
式中,Tm為第m階MSSD 的檢測統計量. 容易得到,Tm服從如下分布

式中,λm為非中心參量
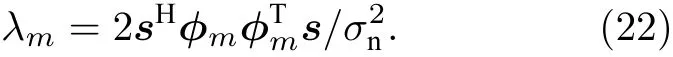
由(21)式可知, 各階MSSD 的自由度都為2,因此其檢測性能僅由對應的非中心參量(λm)唯一決定. 而各階非中心參量的大小迥異, 因而相應的各階MSSD 具有不同的檢測性能.
為更直觀地考量各階MSSD 的檢測性能, 推導了第m階MSSD 的處理增益為(推導過程見附錄)
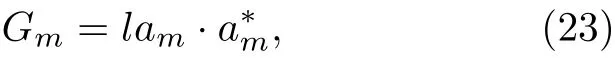
式 中,上 標‘*’表 示 復 數 共 軛運 算,l為 常 系 數.(23)表式明第m階MSSD 的處理增益與相應的模態系數成正比. 將(2)式代入(23)式中可得,
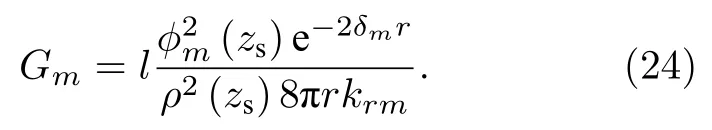
由(24)式可知, 由于各階相異的模態衰減系數δm、聲源深度上的模態函數值?m(zs) 以及水平波數krm, 導致各階MSSD 具有不同的處理增益, 進而表現出不同的檢測性能. 淺海波導中的各階水平波數在數值上相差較小, 因此造成各階MSSD 不同檢測性能的主要因素是聲源深度上的模態函數值和模態衰減系數.
3.2 基于模態衰減加權的子空間檢測器
MSD 為 各MSSD 非 相 干 疊 加之 和, 由 于各MSSD 的處理增益實際上大不相同, 因此對MSD 最終檢測性能的貢獻也各不相同. 處理增益較大的MSSD 為MSD 貢獻更多的信號能量, 處理增益較小的MSSD 則為MSD 主要引入噪聲分量.如果根據各階處理增益的變化規律設計權值對各階MSSD 進行加權求和, 使得到的檢測器具有更大的輸出信噪比, 則最終獲得的檢測器將獲得更好的檢測性能. 基于此, 我們提出一種加權的模態子空間檢測器(weighted modal subspace detector,WMSSD). 結合(20)式, 構造WMSSD 的檢測統計量為
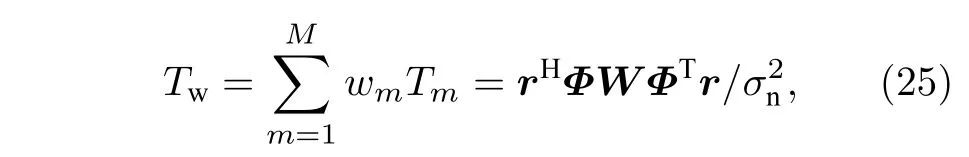
式中,W=diag(w1,··· ,wM) ,wm為第m階MSSD 的加權系數. 將(25)式代入(16)式和(14)式中,可得WMSSD 的處理增益為
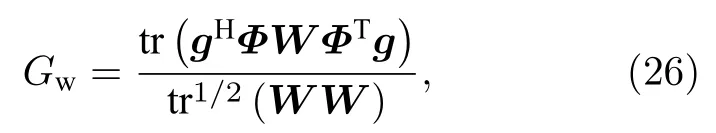
式中, tr(·) 表示矩陣求跡運算. 顯然, 當加權系數等于各階MSSD 的處理增益時, 即權值wm=Gm,WMSSD 可以獲得最優的處理增益, 將相應的檢測器稱為最優加權的模態子空間檢測器(optimal weighted modal subspace detector, OWMSSD).然而由于實際上聲源位置未知, 無法直接計算得到各階處理增益作為加權系數, OWMSSD 并不能實現. 為此, 需要尋求其他次優的加權系數.
根據3.1 節分析可知, 各階MSSD 的處理增益與聲源深度處的模態函數值和模態衰減系數成正比. 簡正波的各階模態函數隨波導深度變化. 在等聲速波導中, 各階模態函數隨深度振蕩變化, 振蕩頻率隨階數的增大而增大. 在非等聲速波導中, 模態函數存在反轉點. 由文獻[16]可知, 各階模態函數在反轉點之間是振蕩變化的, 在反轉點之外呈指數規律迅速衰減. 因此, 不同聲源深度上的各階模態函數值的變化較為復雜. 而各階模態衰減系數的變化規律較為簡單, 隨模態階數的增大而增大. 雖然模態衰減系數在數值上相對于水平波數較小,但對于遠距離傳播的聲信號, 在指數衰減規律( e?2δmr)的作用下, 各階MSSD 的處理增益呈現明顯的衰減, 且衰減程度隨階次增大而增大.
基于上述分析, 可以考慮利用模態衰減系數來設計加權系數. 假設目標聲源位于觀測區域, 觀測區域在距離上的范圍為R ?R1(單位為km), 利用衰減指數設計各階MSSD 的加權系數為
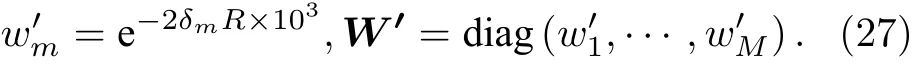
將(27)式代入(26)式中計算可得WMSSD的處理增益. 對于本文考慮的遠距離傳播的聲信號, 模態衰減系數對處理增益的作用較為強烈, 該加權方式能反映各階處理增益的變化趨勢, 因此得到的WMSSD 預期可獲得更大的處理增益, 并實現一定的檢測性能提升.
各階MSSD 的最優加權為其相應的處理增益,各階處理增益由聲源的深度和距離共同決定, 由于本文在設計加權系數時僅考慮了模態衰減系數的影響, 因此得到的WMSSD 的處理增益與聲源深度和距離有關. 聲源深度主要影響的是模態函數值?m(zs) , 模態函數在波導深度上的分布規律主要與聲速剖面有關, 因此WMSSD 的處理增益在聲源深度上的分布規律將受到聲速剖面的影響.
4 仿真實驗與分析
本節將通過仿真實驗驗證WMSSD 的檢測性能相較于MSD 的提升效果, 同時探究WMSSD 的檢測性能隨相關參數的變化規律及造成這種變化的物理機理, 并通過與MSD 的處理增益對比歸納WMSSD 的適用場景. 仿真使用的波導環境模型和VLA 如圖1 所示, 圖中標注了相關的海洋環境參數. VLA 覆蓋整個水深, 陣元個數N=120 , 起始陣元深度為1 m, 陣元間距為1 m. 假設目標位于觀測區域范圍15— 30 km. 仿真中的信噪比為對數信噪比(即 10 lg SNR ), 單位為dB. 聲場與模態深度函數由Kraken 程序計算.
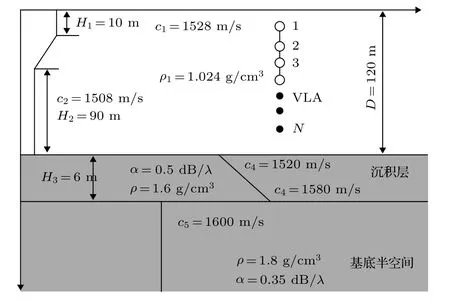
圖1 淺海波導環境及其相關參數Fig. 1. The shallow water waveguide and its environmental parameters.
4.1 MSD 與WMSSD 的檢測性能
假設聲源位于距離為18 km、深度為50 m 處,仿真中通過提高聲源頻率來增大波導中的傳播模態數. 圖2 給出了MSD 的檢測概率隨信噪比和虛警概率變化的曲線, 即檢測性能曲線, 其中窄帶聲源中心頻率f 分別為50, 100, 300, 500 和700 Hz時在波導中激發的傳播模態數分別為3, 5, 16,27 和37. 從圖2 可以看出, 相同信噪比條件下, 隨著傳播模態數的增多, 對應MSD 的檢測概率隨之下降, 下降幅度逐漸減緩.
為進一步探究MSD 檢測性能變化的原因, 圖3給出了不同模態數下MSD 的處理增益, 對圖中處理增益取對數表示, 即10lgG, 單位為分貝(dB).由圖3 可知, 隨著模態個數增多, MSD 的處理增益逐漸減小. 這是由于隨著傳播模態數的增多, 引入了更多的噪聲分量, 而信號能量保持不變, 從而導致MSD 的處理增益下降. 同時也注意到隨模態數的增加處理增益下降的速度在減緩, 這與檢測性能曲線呈現的結果相一致.
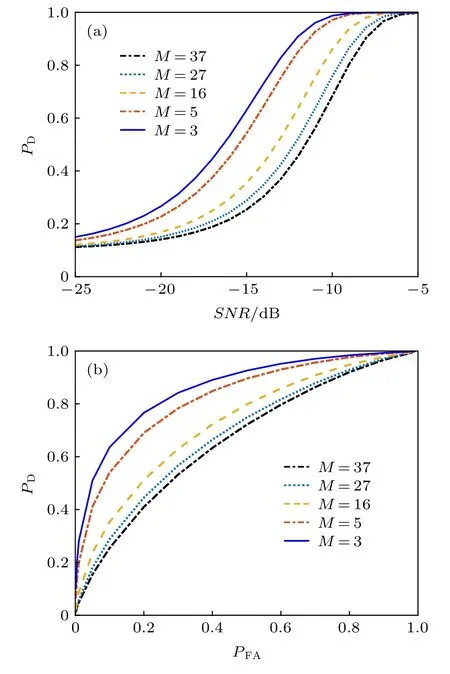
圖2 不同傳播模態數下MSD 的檢測性能曲線 (a) 檢測概率隨輸入信噪比的變化, PFA =0.1 ; (b) 檢測概率隨虛警概率的變化, SNR =?15 dBFig. 2. Detection performance curves of the MSD under various numbers of normal modes: (a) Probabilities of detection versus SNRs, PFA =0.1 ; (b) probabilities of detection versus probabilities of false alarm, SNR =?15 dB .
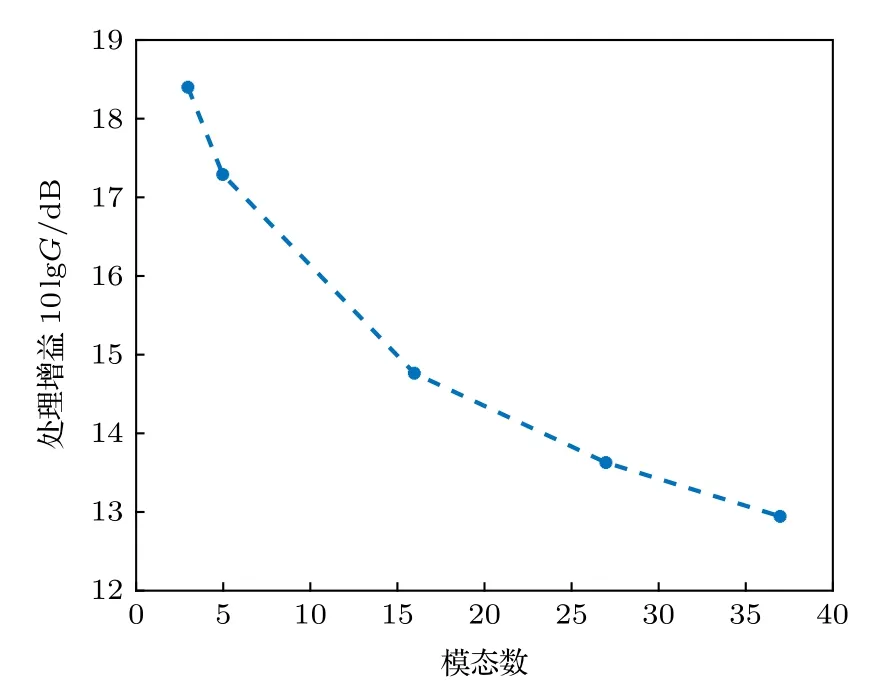
圖3 MSD 的處理增益隨模態數的變化曲線Fig. 3. The processing gains of the MSD versus the numbers of normal modes.
聲源位置同上, 圖4 給出了不同傳播模態數下歸一化的各階MSSD 處理增益(這里為便于展示Gm的變化趨勢未對其取對數)的分布, 其中階數大于8 的處理增益都近似為零, 圖中未予展示. 由圖4 可知, 盡管模態數增多, 處理增益仍主要集中在少數幾階MSSD, 且各階MSSD 的分布呈現隨階數的增大逐漸減小的趨勢; 此外, 還觀察到當傳播模態數較多時, 各階MSSD 的處理增益分布存在起伏. 由文中(24)式可知, 第m 階MSSD 的處理增益不僅與模態衰減系數有關, 它使得MSSD的處理增益隨階數呈下降趨勢; 此外, 第m 階MSSD 的處理增益還與聲源深度上的模態函數幅值 ?m(zs)有關, 由于 ?m(zs) 隨階數振蕩變化, 尤其是當傳播模態數較多時, ?m(zs) 隨階數振蕩變化的更劇烈, 進而使得各階MSSD 的處理增益存在起伏; 例如當M = 37 時, 此時 ?1(zs)
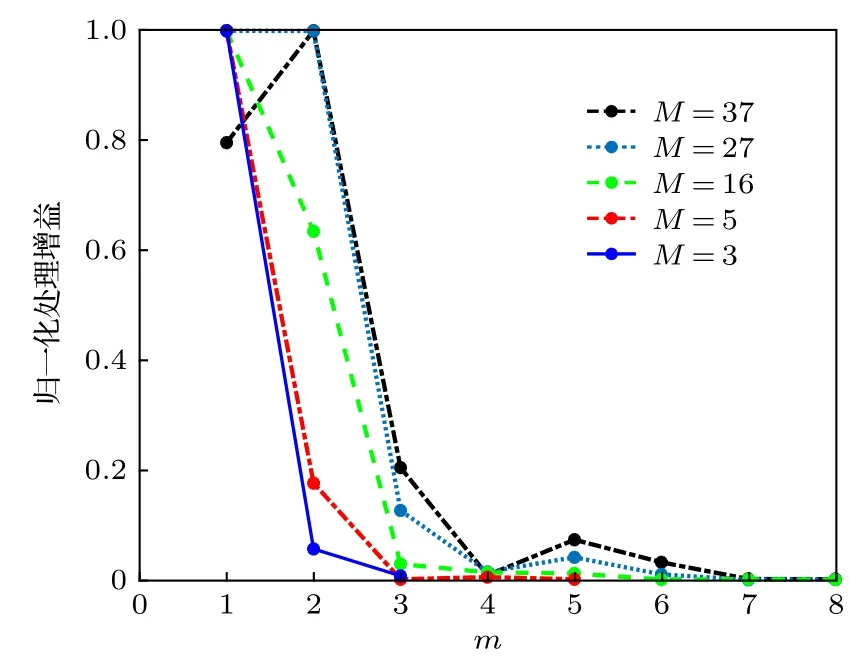
圖4 各階MSSD 處理增益隨階數的變化Fig. 4. The processing gains of MSSD versus the orders of normal modes.
聲源位置同上. 利用(17)式和(26)式分別計算了該聲源位置處MSD, WMSSD 和OWMSSD的處理增益, f = 100 Hz 時對應的處理增益分別為17.41 dB, 20.10 dB 和20.11 dB, f = 300 Hz 時對 應 的 處 理 增 益 分 別14.90 dB, 19.18 dB 和19.25 dB. 可以看出, WMSSD 的處理增益相較于MSD 有很大幅度的提升, 并且接近于OWMSSD.圖5 和圖6 分別給出了這兩種頻率(100 和300 Hz)下相應的MSD, WMSSD 和OWMSSD 的檢測性能曲線. 由圖5 和圖6 可知, 對于該位置的聲源,WMSSD 與OWMSSD 的檢測性能曲線幾乎重合,即WMSSD 實現了理論上所能達到的最優檢測性能, 相較于MSD 有了顯著的提升; 取檢測概率為0.5 時所需的信噪比門限為比較對象(下同), 對于100 和300 Hz 的聲源, WMSSD 的信噪比門限分別下降了1.5 和3 dB. 對比圖5 和圖6 也可看出,雖然WMSSD 對較高頻率聲源的性能提升幅度較大, 但當頻率增大時其檢測性能仍有所下降, 這由傳播模態數增多導致.
4.2 聲源位置對WMSSD 檢測性能的影響
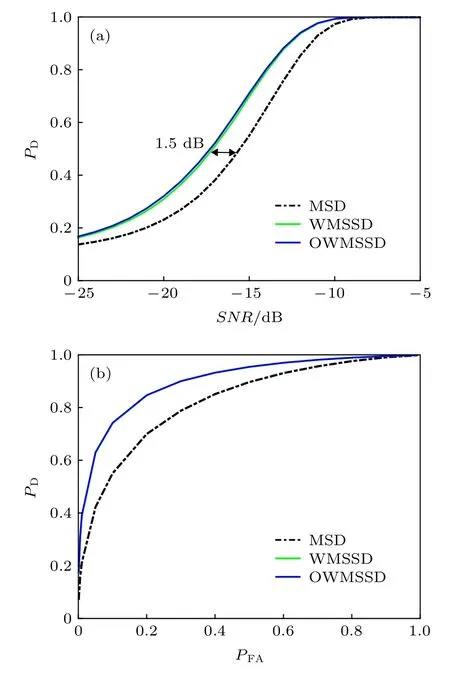
圖5 MSD,WMSSD,OWMSSD的檢測性能曲線,f=100 Hz (a)檢測概率隨輸入信噪比的變化, PFA =0.1 ;(b) 檢測概率隨虛警概率的變化, SNR =?15 dBFig. 5. Detection performance curves of the MSD, WMSSD and OWMSSD with f = 100 Hz: (a) Probabilities of detection versus SNR, PFA =0.1 ; (b) probabilities of detection versus probabilities of false alarm, SNR =?15 dB .
對于相同的信噪比, 處理增益越大, 檢測器的輸出信噪比就越大, 進而檢測器將獲得更優的檢測性能, 因而檢測器處理增益的大小直接反映了其檢測性能的優劣. 各階MSSD 的處理增益與聲源位置(深度和水平距離)直接相關, 而加權系數與聲源位置無關, 因此加權系數并不與各階MSSD 的處理增益完全一致, 這就使得WMSSD的處理增益會受到聲源位置的影響.

圖6 MSD, WMSSD,OWMSSD的檢測性能曲線,f=300 Hz (a)檢測概率隨輸入信噪比的變化, PFA =0.1 ;(b) 檢測概率隨虛警概率的變化, SNR =?15 dBFig. 6. Detection performance curves of the MSD, WMSSD and OWMSSD with f = 300 Hz: (a) Probabilities of detection versus SNR, PFA =0.1 ; (b) probabilities of detection versus probabilities of false alarm, SNR =?15 dB .
為充分了解WMSSD 的檢測性能, 我們給出了當聲源(頻率為300 Hz)位于不同深度和距離時WMSSD 的處理增益(單位為dB), 同時作為對比也給出了MSD 和OWMSSD 的處理增益隨聲源位置的變化, 如圖7 所示. 由圖7(a)和圖7(b)可知, MSD 的處理增益基本穩定在14.85 dB 左右, 隨聲源位置波動很小, WMSSD 的處理增益變化范圍較大, 在5—20 dB 之間波動. 但同時也注意到, 事實上只有一小塊區域WMSSD 的處理增益較小(小于MSD), 而大部分區域上的處理增益都在較大數值范圍內波動. 圖7(b)中標示出了處理增益小于MSD 的區域, 將該區域稱為WMSSD的弱探測區域, 即黑色實線左上角部分, 在其他區域WMSSD 的處理增益均大于MSD. 記WMSSD與MSD 處理增益相同的深度為臨界深度, 可以看出臨界深度隨距離增大而減小, 到24 km 處時減小為零, 即當聲源距離大于24 km 時, WMSSD 的弱探測區域消失. 同時注意到在深度為60—80 m范圍內, WMSSD 的處理增益達到最大, 都在18 dB 以上, 且隨距離的波動較小. 由圖7(c)可知,OWMSSD 的處理增益總是大于MSD 和WMSSD,且它在不同位置的變化規律與WMSSD 類似.
圖7 中的數值結果表明, 在大部分情況下,WMSSD 的檢測性能明顯優于MSD, 但當聲源深度位于臨界深度以淺時, 其檢測性能要差于MSD,同時臨界深度隨距離的增大而減小. 這是由WMSSD 的加權方式造成的. 在設計加權系數時只考慮了模態衰減的影響, 而各階MSSD 的處理增益不僅與模態衰減系數有關, 還與聲源深度上的模態函數值 ?m(zs) 有關, 聲源深度上的各階模態函數值使得WMSSD 的處理增益隨聲源位置的改變而改變.
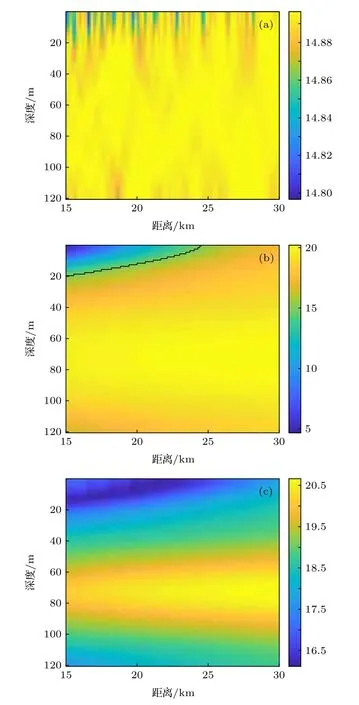
圖7 MSD, WMSSD, OWMSSD 的處理增益隨聲源位置的變化, f = 300 Hz (a) MSD; (b) WMSSD; (c) OWMSSDFig. 7. The processing gains of the MSD, WMSSD and OWMSSD versus acoustic source locations with f = 300 Hz:(a) MSD; (b) WMSSD; (c) OWMSSD.
4.3 WMSSD 處理增益變化機理分析
波導環境中的模態函數主要取決于聲速剖面.在非等聲速波導中, 各階模態函數以反轉點深度為臨界, 在波導垂直尺度上呈現不同的分布規律, 而反轉點的位置主要與波導中的聲速有關, 因此WMSSD 的處理增益還受到聲速剖面的影響. 反轉點深度處的聲速滿足如下關系式[16]
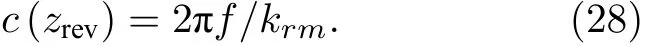
式中,zrev為反轉點處深度. 由(28)式可知, 由于各階水平波數不同, 各階模態深度函數具有迥異的反轉點深度. 由于各階水平波數隨階數增大而逐漸減小, 高階模態函數的反轉點處聲速更大. 因此對于負梯度聲速剖面, 各階模態函數的反轉點深度將隨階數增大而變小. 以圖1 中的負梯度聲速波導為例, 各階模態函數及其反轉點深度如圖8 所示. 由圖8(b)可知, 反轉點深度隨階數增大而逐漸變小.結合圖8(a)可知, 在反轉點以淺, 模態函數呈指數迅速衰減, 相應的模態函數值很小; 在反轉點以深,模態函數呈周期性的振蕩變化. 對于較高階模態函數, 若c(z)<2πf/krm對所有深度都成立, 此時不存在反轉點或者說反轉深度為零, 如圖8(b)中第8 階及以后的模態函數不再存在反轉點.

圖8 各階模態函數及其反轉點深度, f = 300 Hz (a) 波導環境中的各階模態函數分布; (b) 各階模態函數的反轉點深度Fig. 8. The modal depth functions and their turning-depths with f = 300 Hz: (a) Each modal depth function in the waveguide; (b) the turning-depth of each modal depth function.
當聲源位于若干階模態函數的反轉深度以淺時, 相應的聲源模態幅值?m(zs) 很小, 這種情況下由于聲源模態幅值的作用, 各階MSSD 處理增益的變化趨勢為低階和高階較小, 中階較大, 這與加權系數的變化趨勢不一致, 如圖9(a)所示, 導致WMSSD 的處理增益較差并小于MSD. 當聲源位于各階反轉深度以深時, 加權系數較大程度地刻畫了各階MSSD 處理增益的變化趨勢, 如圖9(b)所示, 進而WMSSD 的處理增益較大并大于MSD.當聲源位于某一深度上時, WMSSD 的處理增益與MSD 相等, 該深度即為圖7(b)中的臨界深度.
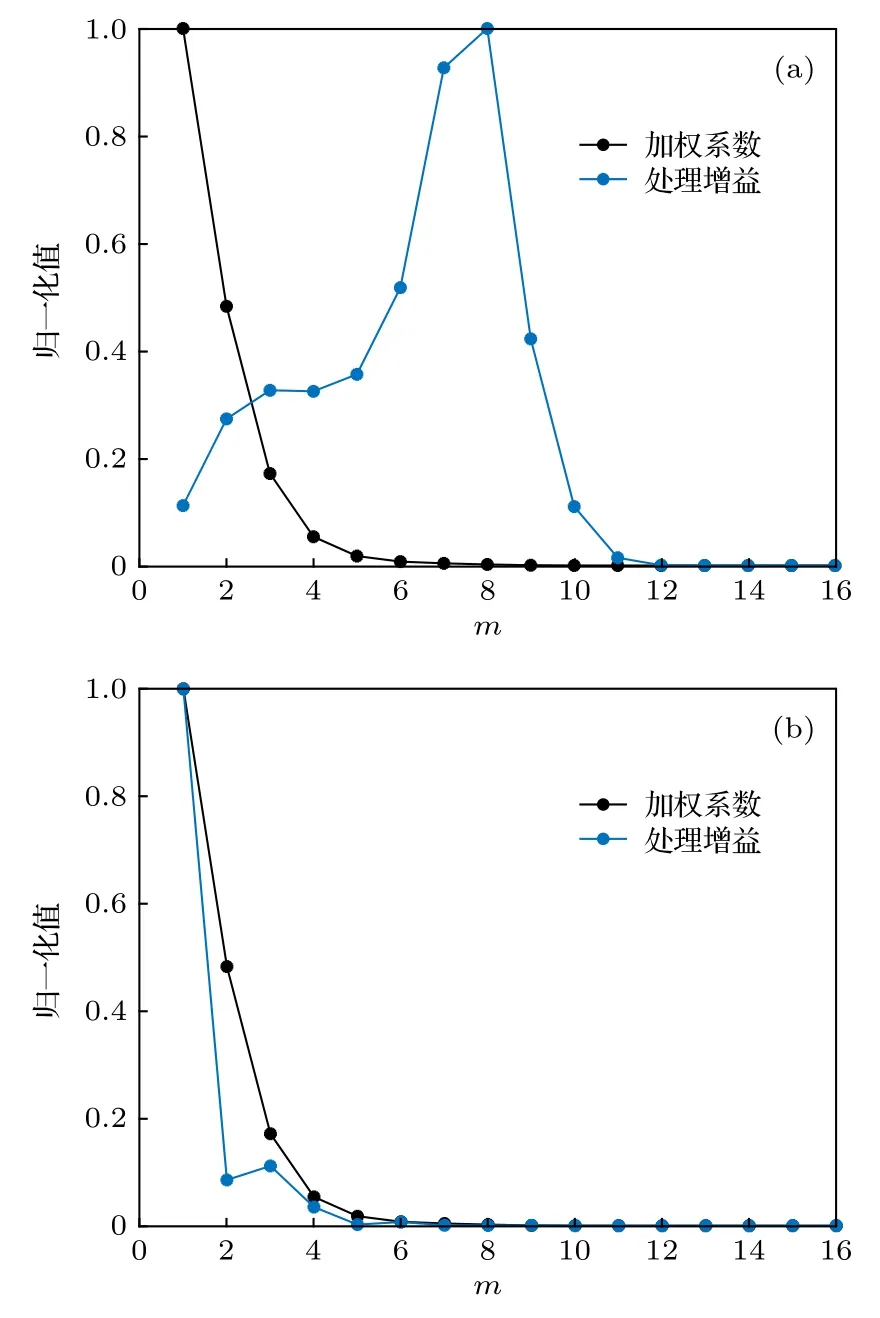
圖9 各階MSSD 的加權系數與處理增益, f = 300 Hz, 聲源距離15 km (a)聲源深度10 m; (b) 聲源深度80 mFig. 9. The weighting coefficients and the processing gains of the MSSD with f = 300 Hz and source range of 15 km:(a) Source depth of 10 m; (b) source depth of 80 m.
對于不同頻率的聲源, 臨界深度隨聲源距離的變化如圖10 所示. 由圖10 可知, 臨界深度隨聲源距離的增大而減小. 這是由于當聲源距離增大時,衰減指數的作用更加劇烈, 信號能量更多的集中在低階MSSD, 相較于圖9(a), 圖11 所示的各階MSSD 歸一化的加權系數與處理增益的變化趨勢更加一致, 進而WMSSD 的處理增益提高, 臨界深度變淺. 同時由圖10 可以看出, 隨聲源距離增大低頻聲源臨界深度更快減小為零. 這是由于當聲源頻率增大時, 模態個數增加, 存在反轉點的模態數也增多, 因而聲源模態幅值的影響增大, 最終導致臨界深度隨聲源距離的變化速率減緩.
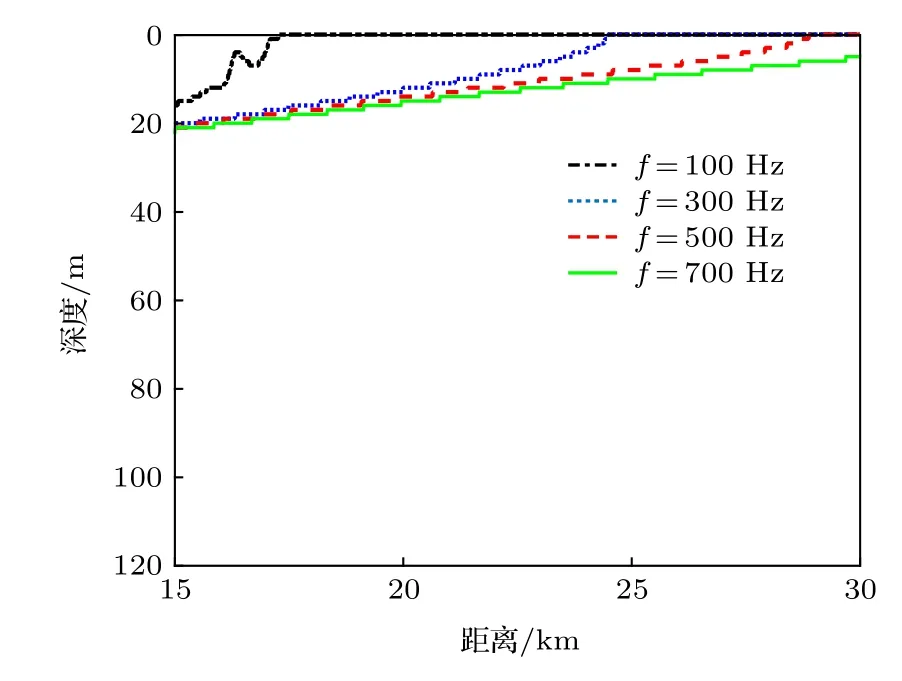
圖10 不同頻率時臨界深度隨距離的變化圖Fig. 10. The critical depths versus ranges under various frequencies.
4.4 聲速剖面對WMSSD 處理增益的影響分析
上文討論了負梯度聲速波導中WMSSD 處理增益的變化規律, 結果表明, 模態函數存在反轉點使得WMSSD 不可避免地出現弱探測區域, 并產生了臨界深度. 模態函數的反轉點深度由波導環境中的聲速剖面決定, 在等聲速波導中模態函數不存在反轉點, 在正梯度聲速波導中反轉點深度將隨模態階數的增大而變大.
考慮等聲速和正梯度聲速的情況, 這兩種聲速剖面如圖12 所示, 其他環境參數同圖1,f=300 Hz. 根據環境參數和(28)式計算可得, 這兩種聲速剖面下聲源在波導中都激發了15 階模態, 各階模態的反轉深度如圖13 所示. 由圖13 可知, 等聲速波導中各階模態不存在反轉深度, 正梯度聲速波導中各階模態的反轉深度隨階數增大而變深. 相應的各階模態函數如圖14 所示, 在正梯度聲速中,第1—5 階模態函數存在反轉點, 在反轉點深度以深, 模態函數呈指數衰減, 幅值接近于零, 在反轉點深度以淺及高階模態, 模態函數以一定周期振蕩變化, 這與負梯度聲速下的變化規律相反.
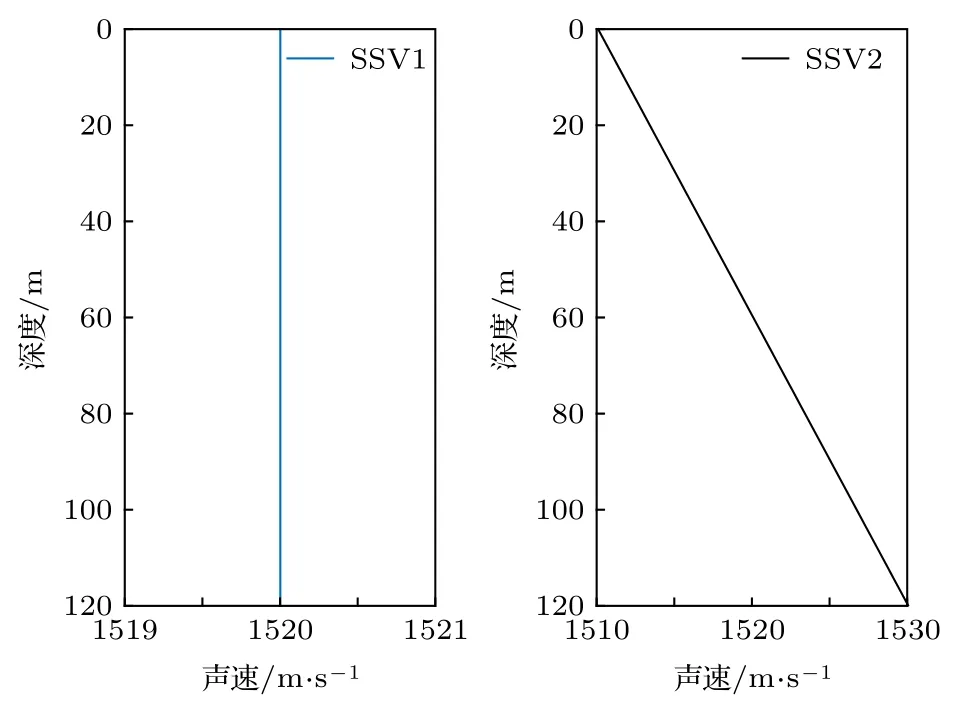
圖12 等聲速剖面與正梯度聲速剖面圖Fig. 12. Constant sound velocity profile (SVP) and positive gradient SVP.
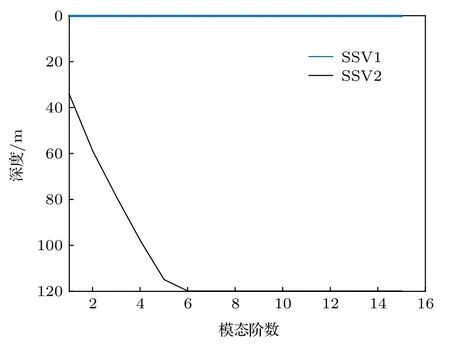
圖13 各階模態函數的反轉深度, f = 300 HzFig. 13. The turning-depth of each modal depth function with f = 300 Hz.
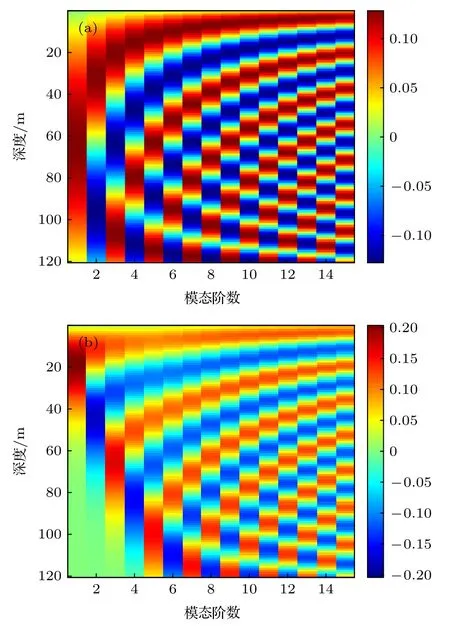
圖14 兩種聲速剖面波導中的各階模態函數, f = 300 Hz (a) 等聲速剖面; (b) 正梯度聲速剖面Fig. 14. Each modal depth function in the two kinds of waveguides with f = 300 Hz: (a) Constant SVP; (b) positive gradient SVP.
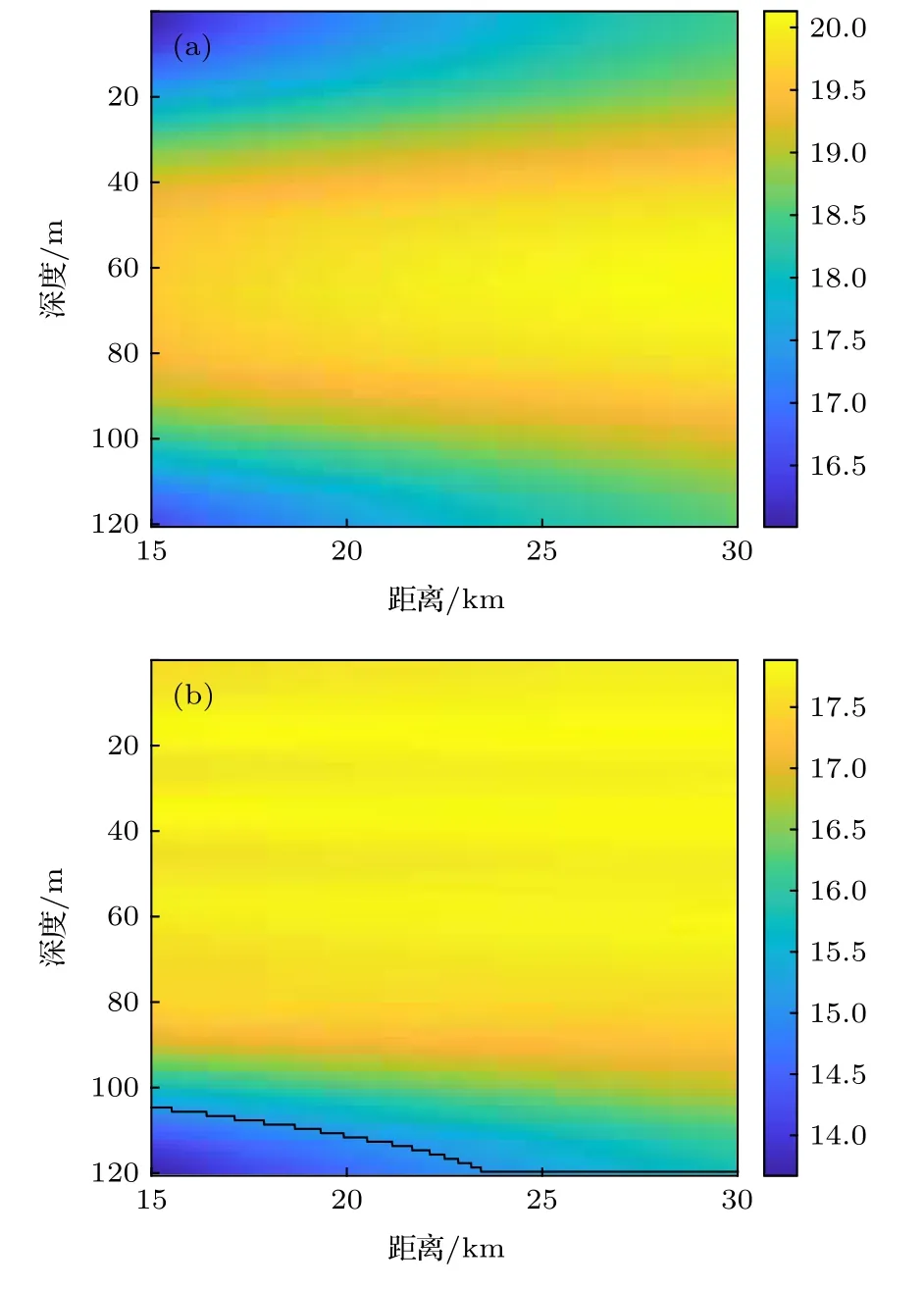
圖15 兩種聲速剖面下, 不同聲源位置處的WMSSD 處理增益, f = 300 Hz (a)等聲速剖面; (b) 正梯度聲速剖面Fig. 15. The processing gains of the WMSSD versus acoustic source locations with f = 300 Hz: (a) Constant SVP;(b) positive gradient SVP.
圖15給出了兩種聲速剖面波導下WMSSD的處理增益(單位為dB), 圖中黑線標出了不同距離上的臨界深度. 在等聲速波導中, 各階模態函數不存在反轉點且呈周期振蕩變化, 聲源深度上模態函數幅值對各階MSSD 處理增益的影響較小, 因此當聲源位于不同深度上時, 各階MSSD 處理增益的變化趨勢總是與各階衰減指數相一致, 使得WMSSD 的處理增益在所有深度上都大于MSD,因此不存在臨界深度, 如圖15(a)所示. 在正梯度聲速波導中, 各階模態函數的反轉深度隨階數增大而增大(與負梯度聲速的情況相反), 在反轉點以深, 模態函數呈指數衰減, 并很快接近于零. 當聲源位于若干階模態的反轉深度以深時, 聲源模態幅值對各階MSSD 的非中心參量產生顯著影響, 且隨著深度增加, 產生的影響也增大. 因此, WMSSD的處理增益下降, 進而出現臨界深度, 在臨界深度以深WMSSD 的處理增益小于MSD, 如圖15(b)所示. 而在臨界深度以淺的大部分區域, WMSSD的處理增益大于MSD. 臨界深度隨距離變化的原因與負梯度聲速波導相同. 對比圖15(a)和圖15(b)也可知, 等聲速波導中WMSSD 的處理增益大于正梯度聲速波導.
綜合上述分析可得, WMSSD 在等聲速波導中的穩健性最好, 即對位于所有位置區域的聲源, 都具有大于MSD 的處理增益. 在負梯度聲速波導和正梯度聲速波導中, 雖然WMSSD 的性能穩健性有所下降, 即存在部分的弱探測區域, 但對位于其他大部分區域的聲源, WMSSD 的處理增益都大于MSD.
5 結 論
本文研究了淺海波導中的子空間檢測——模態空間檢測方法, 根據各階簡正波模態在傳播過程中的衰減規律, 提出了一種基于模態衰減系數加權的子空間檢測器——WMSSD. 通過理論分析和仿真實驗探究了WMSSD 的檢測性能及其對聲源位置的穩健性, 結果表明: 1) MSD 的處理增益與聲源在波導環境中激發的模態階數成負相關, 因此當聲源和環境參數變化(如聲源頻率升高、波導深度增大等)使波導中的模態個數增多時, MSD 的處理增益下降導致其檢測性能降低, 這對遠距離傳播的低信噪比目標檢測尤為不利; 2) WMSSD 的檢測性能與聲源位置和聲速剖面有關, 在等聲速波導中WMSSD 的性能穩健性最好, 其處理增益總是好于MSD; 3) 對于負梯度聲速波導和正梯度聲速波導, 由于若干低階模態函數存在反轉點, 造成WMSSD 存在部分弱探測區域, 即當聲源分別在靠近海面和海底的部分區域, 其處理增益相較于MSD 有所下降, 而在其他大部分區域, WMSSD的處理增益相較于MSD 都有顯著的提升.
附錄A
由文獻[20]可知, 對于二次型檢測器,

式中,x表示待檢測數據,A表示加權矩陣, 其輸出信噪比可由下式計算:
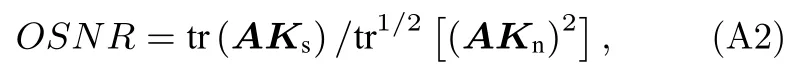
式中,Ks表示信號協方差矩陣,Kn表示噪聲協方差矩陣,tr(·) 表示求矩陣的跡運算.
對于本文中的MSD,
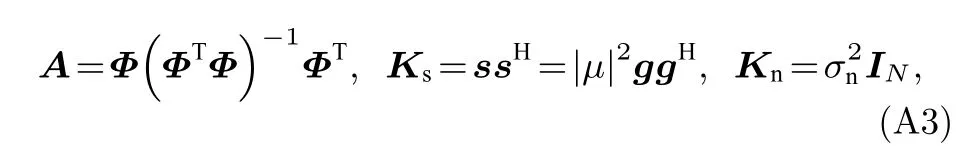
進而可得,
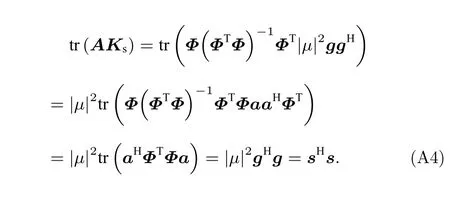
由正交投影矩陣為冪等矩陣且它的跡等于其秩可得,
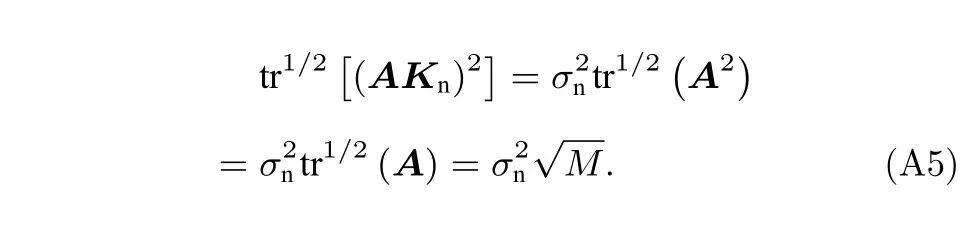
將(32)式和(33)式代入(30)式中可得
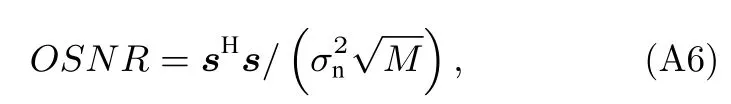
進而可得MSD 的處理增益為
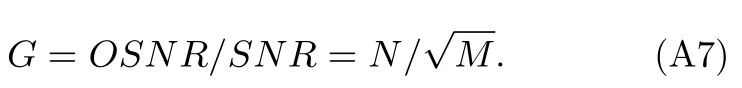
對于第m階MSSD,
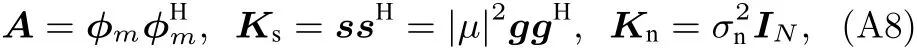
進而有
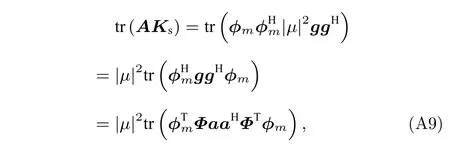
由?1,··· ,?m之間的近似正交性可得
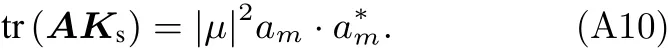
將(38)式和(33)式代入(30)式中可得MSSD 的輸出信噪比為
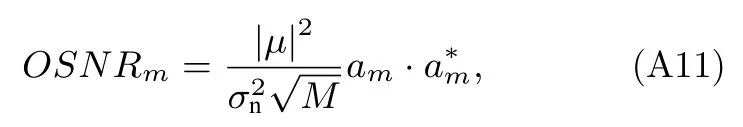
進而可得其處理增益為


