舵系直接計算法設計

田 野， 張文斌， 王 平， 于 博， 楊 營， 張光濤

(1.渤海船舶重工有限責任公司， 遼寧 葫蘆島 125004；2.渤海船舶職業學院， 遼寧 葫蘆島 125004)

0 引 言

在舵裝置的設計過程中，確定舵葉尺寸及布置后需通過計算確定舵系中各部件的尺寸。

在整個舵裝置中，舵桿為重要組成部件之一，可將舵機發出的扭矩傳遞給舵葉。舵干主要受彎曲、扭曲和剪切應力，并且其為運動部件，因此對其受力情況進行準確計算對最終的尺寸選取尤為重要。

目前大型船舶通常采用半平衡懸掛舵，這種型式的舵可以兼顧各部件的強度和設計，易于操作和建造。

現以“渤船”第五代蘇伊士油船舵裝置設計為基礎，對直舵桿型式的半平衡懸掛舵進行計算。

1 直接計算法的使用

目前整個舵系計算的主要依據為規范推薦的經驗公式。經過對幾個船級社規范推薦的經驗公式[1-4]進行研究和對比發現，經驗公式的計算過程基本一致，僅在細節要求上有所差別。舵系計算過程如下：

第一步，根據船舶主尺度、最大吃水和航速等信息計算舵葉受力；

第二步，根據舵葉受力計算需要的舵機扭矩，選取舵機容量；

第三步，通過具體的受力分析計算舵銷、舵承等部位的受力和彎矩；

第四步，根據第三步的計算結果，計算舵葉板厚度、舵桿/銷直徑等。

各船級社計算公式在第一、第二和第四步基本一致，只有在第三步有所區別，得到的結果也不盡相同。下舵承處的彎矩MB對最終確定舵桿直徑有直接關系，而MB并無準確計算公式。

在查閱較多資料后發現，國內各大設計院在舵系設計時使用專用軟件進行受力計算，如DNV的3D-Beam軟件等。然而，這些計算軟件均為付費軟件，且使用這些專業軟件需要一定的設計基礎。在無此設計條件時，只能按照教材[5]和工程手冊中的傳統力學分析方法和公式對舵系模型進行分析，推導出實用的簡化公式進行直接計算。另外可按照簡化公式編寫自動計算表格程序，用來快速準確地計算各參數。

2 力學模型簡化

按照結構及布置，整個半平衡懸掛舵系可視為帶彈性支座的簡支梁，掛舵臂對舵系起彈性支撐作用。半平衡懸掛舵受力分析簡化模型如圖1所示。圖1中：h為舵葉形心至下舵承的距離，m;P1為舵葉缺口下部計算均布載荷,N/m；P2為舵葉缺口上部計算均布載荷,N/m；l1為均布載荷P1長度,m；l2為均布載荷P2長度,m；l3為舵葉頂部至下舵承長度，m；l4為下舵承至上舵承長度，m。

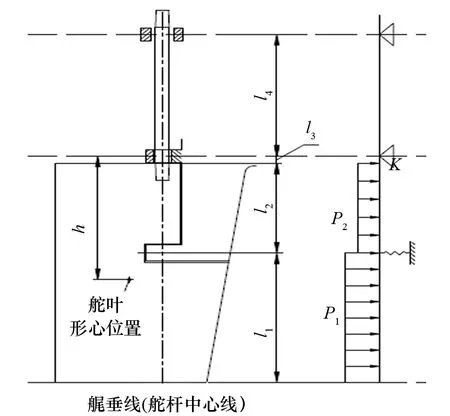
圖1 半平衡懸掛舵受力分析簡化模型

進一步將整個舵系視為3個單獨力分別作用在簡支梁跨外段上，3個力作用下的C點總位移Y等于3個單獨力作用下的位移之和。舵桿的計算模型如圖2所示。

圖2 舵桿計算模型

3 直接計算法公式

查閱各種設計手冊和資料未見可直接用于圖2(b)和圖2(c)模型的撓曲線方程及轉角公式。因此，需進一步將此模型分解，并找到對應的撓曲線方程及轉角公式。

分解后的模型與文獻[6]中一端固定，B點鉸接，在B點外均布載荷的基礎模型相近，而該模型有準確的撓曲線方程及轉角公式。因此，從該基礎模型出發，進行合理的變換，可得到適用于舵系計算的直接計算公式。

一端固定，B點鉸接，在B點外均布載荷的基礎模型如圖3所示。

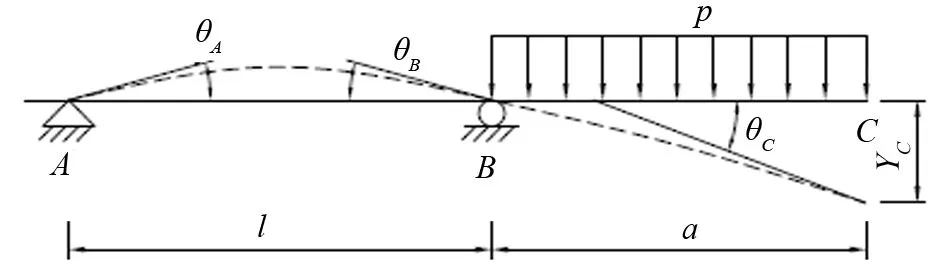
圖3 基礎模型

(1) 端截面轉角

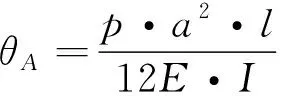
(1)

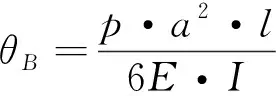
(2)

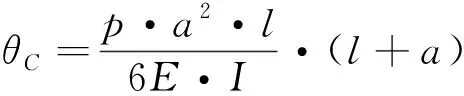
(3)

式(1)～式(3)中：p為模型計算載荷，N/m；a為計算載荷p的長度，m；E為材料彈性模量；I為慣性矩。

(2) 最大撓度

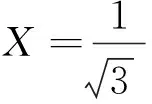
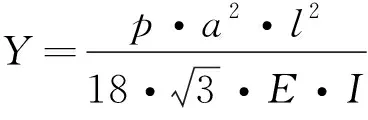
(4)

在X=1+a時：

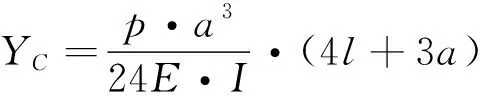
(5)

可將舵系簡化后的模型用2個一端固定、B點鉸接、在B點外跨均布載荷梁的基礎模型組合得到，如圖4所示。

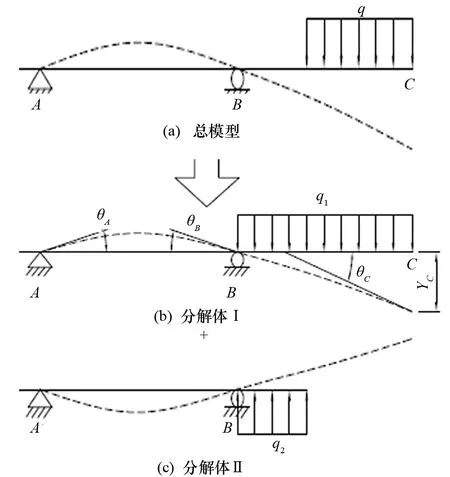
圖4 計算模型分解

圖2(b)和圖2(c)均可進行模型分解，結合舵系布置，可推導出均布載荷q1和q2，以及集中力對舵系C點產生的位移Y為

Y=Y1+Y2+Y3

(6)

(1) 均布載荷q1引起C點的位移Y1計算公式為

(l2+l3+l4)+l1[3(l2+l3)+2l4]}

(7)

(2) 均布載荷q2引起C點的位移Y2計算公式為

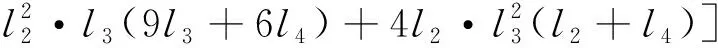
(8)

(3) 集中力引起C點的位移Y3計算公式為

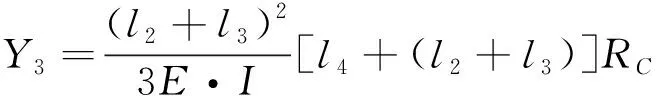
(9)

式中：RC為舵桿在C點的支反力。

“渤船”第五代蘇伊士油船舵裝置計算用數據：P1為均布載荷，取318 640 N/m；P2為均布載荷，取272 820 N/m；E取2.1×1011N/m2；I取(π·D2)/64 mm2；D為計算用舵桿直徑，取585 mm；l1取7.2 m；l2取5.0 m；l3取0.4 m；l4取6.775 m。

將對應的計算數據代入式(7)～式(9)，可得到：Y1= 0.408 05 m；Y2= 0.603 96 m；Y3= 9.802 2×10-8RC。

C點受力產生的位移Y為

Y=Y1+Y2+Y3=0.408 05 m+

0.603 96 m+9.802 2×10-8RC

(10)

根據模型可得，在C點位置由掛舵臂給予舵葉一個彈性支撐，因此C點支座反力公式為

RC=Y·Kh

(11)

式中：Kh為掛舵臂支撐彈性系數，僅與掛舵臂結構有關，Kh取6.9×108N/m。

聯合求解式(10)和式(11)可得RC= 4 745 261 N，Y= 0.006 88 m。

下舵承處舵桿彎矩MB為3個分力對下舵承(B點)計算彎矩之和：MB=P1·l1(l3+l2+l1/2)+P2·l2(l3+l2/2)-RC(l3+l2)= -1 020 650 N·m。

4 復核下舵承處舵桿直徑

在計算過程中需先期輸入舵桿慣性矩等數據，這就需要在計算時假定舵桿直徑，在計算完成后再根據規范要求的公式對假定的舵桿直徑進行校核。

下文從應力和規范要求兩方面進行校核計算。

4.1 應力校核

文獻[3]規定，當使用直接計算法校核舵桿強度時，舵桿的等效應力σe不超過許用應力 [σe]，等效應力計算式為

正應力

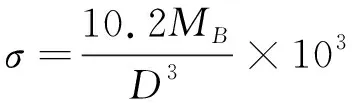
(12)

計算得σ=-52.0 N/mm2。

切應力

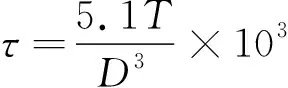
(13)

式中：T為舵葉計算扭矩，取2 405 835 N·m。

計算得τ=61.3 N/mm2。

等效應力

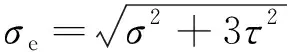
(14)

式中：τ為舵桿切應力。通過計算得σe=118.2 N/mm2。

許用應力

[σe]=118KS

(15)

式中：KS為舵桿材料系數。

計算得[σe]=113 N/mm2。

計算結果顯示σe> [σe]，因此假定的舵桿直徑不滿足規范要求。

4.2 規范校核舵桿直徑

根據CCS規范復核下舵承處舵桿直徑[3]：

(16)

式中：Dt為舵柄處傳遞舵扭矩的舵桿直徑。

計算得D=580.4 mm < 585.0 mm (直接計算法假定直徑)，因此假定的舵桿直徑滿足規范要求。

4.3 重新迭代計算

根據第4.1節和第4.2節的校核結果，若假定的舵桿直徑不滿足要求，則需增大計算中假定的舵桿直徑重新進行計算，直到滿足要求為止。第4.1節計算結果顯示，下舵承處舵桿直徑選擇585.0 mm不滿足應力校核要求，因此增大舵桿直徑進行重復計算。舵承處舵桿彎矩MB校核等計算結果如表1所示。

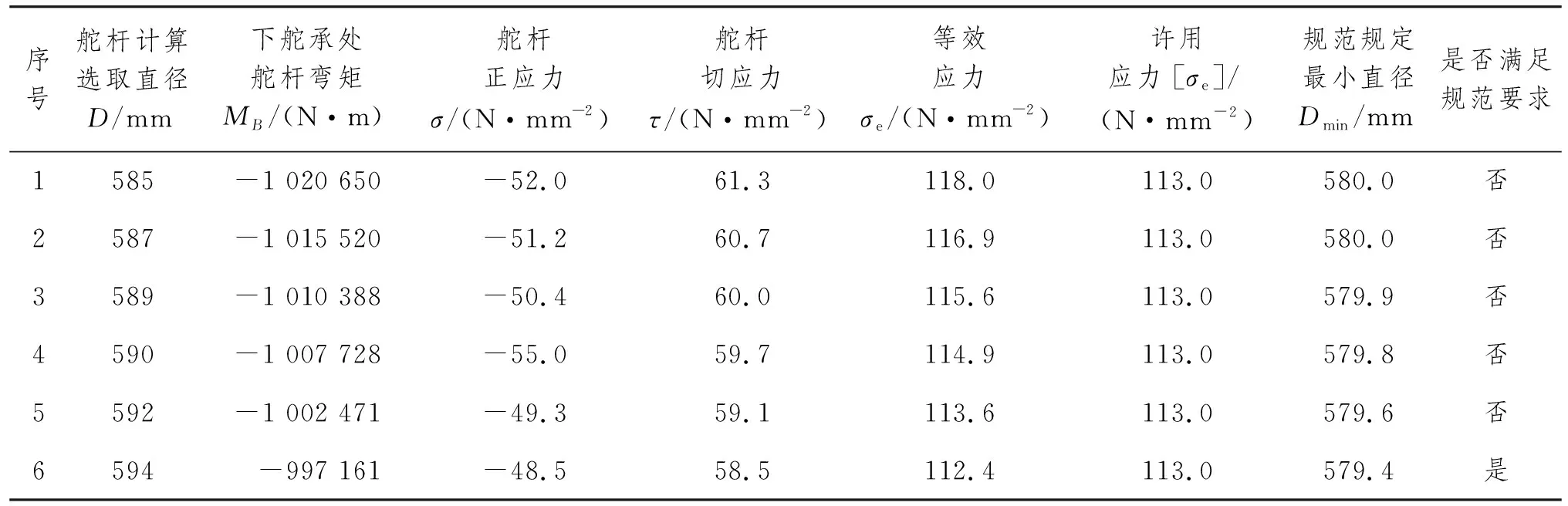
表1 校核計算及迭代計算結果匯總

5 結 論

各船級社推薦公式與直接計算法所得結果匯總如表2所示。由表2可知，船級社推薦的公式均非常保守，在實際使用過程中有大量冗余。采用直接計算法可使下舵承處舵桿直徑減少10%左右，大幅降低設計成本。

表2 各船級社推薦MB計算公式及直接計算法對比

因此，采用直接計算法進行舵系計算并確定舵桿直徑等參數，對新項目的設計和開發具有重要意義，可提高設計效率、降低建造成本，提高船舶的經濟性和市場競爭力。