一種基于序列到序列時空注意力學習的交通流預測模型

杜圣東 李天瑞 楊 燕 王 浩 謝 鵬 洪西進

1(西南交通大學信息科學與技術學院 成都 610031)2(臺灣科技大學計算機科學與信息工程系 臺北 10607)(sddu@swjtu.edu.cn)

隨著城市化進程的加速發展，交通擁堵、尾氣排放等問題導致城市交通管理面臨挑戰，如何有效預測未來的交通流趨勢以提前干預疏導，被認為是智能交通管理決策需解決的關鍵問題之一[1].一般來講，觀測點采集到的交通流量表示每個時間間隔通過的車輛數量，采集到的流量數據還包括交通速度、通行時間和道路情況等多個屬性.由于復雜的交通路網和越來越龐大的車輛數量，通常采集到的與交通流相關的時空序列數據具有數據規模大、高維度、動態性和突變性等特征，因此傳統的時間序列分析方法越來越難以對其進行有效建模和預測[2].而且，很多傳統的交通流預測模型通常僅限于單步預測，但在實際應用中，需要能提前預測多個時間步長后的交通流量變化情況，這對智能化的交通管理和擁堵分析預警來講至關重要.

在過去幾十年中，許多研究者提出了各種城市交通流量預測方法，并取得了一系列理論和應用研究成果[3].這些研究中的大多數方法主要基于統計模型或淺層機器學習方法來描述交通網絡流量的演變，例如ARIMA[4]，ANN[5]和SVR[6]等.但是交通流量變化通常會受到出行、天氣、事故等因素的影響，而且呈動態變化趨勢，因此傳統方法面臨較大的瓶頸.另外，隨著交通大數據的發展，基于物聯網技術采集到的真實交通數據通常是多變量時空序列，往往包括多個變量屬性，例如交通流量、交通速度、交通密度、交通路程時間(通過時間)等.由于交通狀況的快速變化，在非一般性交通流動的情況下(例如高峰時段、事故發生時段等)，交通流量預測面臨很大的挑戰，因為交通流受上述多個變量屬性的影響，交通相關時間序列數據通常具有非線性或突變性特點，而且相互影響依賴.如圖1所示，僅僅交通流量與通行速度兩者就有著非線性相關聯系.如何讓模型學習到交通時序數據中的多個變量之間的非線性相關特征，對于有效的交通流預測建模來講十分重要.

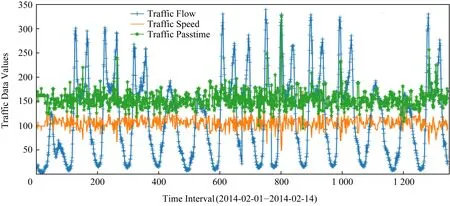
Fig. 1 Nonlinear correlation diagram of multivariate traffic flow related time series data圖1 多變量交通流相關時序數據的非線性相關示意圖

另外，眾所周知，相鄰交通網絡節點之間的交通狀況是相互影響和依賴的，如何分析和利用這種相互依賴性,如圖2所示，不同位置采集點的交通流數據存在時空關聯性，包括不同采集站點的空間依賴性，和同一采集點在不同時間步下的交通流長時依賴性，這對于提高交通流預測模型的性能也很重要.如何針對上述2個關鍵點：一個是學習到多變量時空序列之間的非線性相關性特征，另一個是學習到多站點交通流序列之間的時空關聯性特征，是所提出的序列到序列時空注意力學習模型要解決的核心問題.

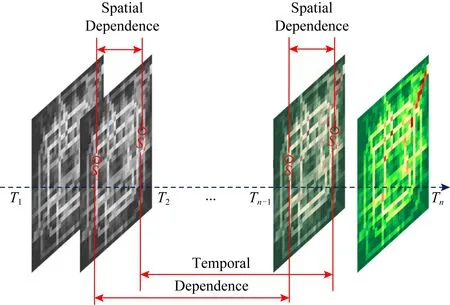
Fig. 2 Spatiotemporal correlation diagram of traffic flow data collected at different locations圖2 不同位置采集點的交通流數據時空相關性示意圖

深度學習由于其多層非線性映射原理的深度特征抽取學習能力，如在圖像處理、語音識別和自然語言處理等多個領域取得突破性進展[7-9].由于不同交通時序數據之間通常存在復雜的非線性時空相關關系，傳統方法模型難以挖掘與交通流量相關的各類城市時空序列數據之間的深層關系，而深度學習方法對于交通流預測任務來講是一個很好的選擇，因此也越來越受到研究者們的關注[10-11].這也是為什么提出新型的深度學習模型來進行交通流量預測研究.針對上述2個關鍵問題，提出了一種基于序列到序列學習結構并結合時空注意力學習機制的深度學習模型.該模型采用序列到序列學習框架，基于卷積LSTM并擴展編碼器解碼器的時空注意力學習模塊，以自動學習多變量交通時空序列數據中的隱含時空表示和長時空依賴相關性深度特征.研究貢獻主要包括3個方面：

1) 提出了一種新的基于時空注意力機制的序列到序列端到端深度學習模型，并將其應用于多變量交通時空序列建模任務.通過基于卷積 LSTM和擴展時空注意力模塊的編碼器，將交通時空序列數據中的深度時空特征編碼為時空上下文向量，另一個LSTM用于解碼時空向量以進行預測.

2) 引入了編碼器網絡與解碼器網絡之間的時空注意力學習機制，可以在所有時間步中選擇與預測目標更相關的編碼器隱藏狀態，從而提高模型對多變量交通時空序列數據的深度表示能力，使得該模型可以學習到多變量交通時空序列數據中的長時空依賴特征和非線性相關等特征.

3) 基于3個真實的交通數據集實驗，實驗結果表明，該模型具有良好的預測性能和多步交通流預測能力，而且所提出模型的預測性能要優于其他基準模型.

1 相關工作

一直以來，為了提高智能交通的擁堵分析與管理決策能力，研究人員提出了大量的交通流量預測模型[1]，其中大部分研究基于經典統計方法或淺層機器學習方法.例如Williams等用ARIMA對交通流進行建模，該方法為將單變量交通流序列數據建模為自回歸移動平均過程，從而進行交通流預測[4].Chan等人[5]提出了一種使用混合指數平滑策略和Levenberg-Marquardt優化的ANN模型，以支持短時交通流量預測.Zhao等人[12]采用高斯過程模型對交通流進行建模，并提出了基于四階高斯過程的動態交通流預測模型，該模型使用神經網絡來訓練模型參數.Sun等人[13]通過分析相鄰路段的交通流量影響關系，提出了基于貝葉斯網絡的交通流量預測方法.Lippi等人[3]在概率圖模型的通用視圖下，回顧了現有的短時交通流量預測方法，并進一步進行了實驗比較和性能分析.

最近幾年，隨著智慧城市的高速發展[14]，交通時空大數據呈爆炸式增長，數據建模面臨的高維度、動態性和非線性相關性等問題越來越突出.一些研究人員嘗試使用數據驅動的深度學習方法進行時間序列預測分析和建模[15-16]，深度學習自然也成為了交通流預測研究的熱點[2].深度學習由于其捕獲非線性深度特征的能力而受到廣泛關注，當然也可用于自動提取和學習城市時空序列數據中的深層次表示.由于交通擁堵過程和交通流演化本質上是動態變化、多因素非線性相關和序列突變的[17]，因此深度學習模型無需先驗知識即可學習交通時空數據的深層特征，這也非常適合處理交通流建模問題.因此，越來越多的研究者提出了基于深度學習的交通流量預測模型[10-11,18].例如Lv等人[10]提出了一種基于深度學習的交通流量預測方法，該方法采用堆疊式自動編碼器模型來學習交通流量數據中的深層次特征和時空相關性.Huang等人[11]在交通流研究中也應用了深度學習方法，該方法將多任務學習納入了深度學習架構，通過實驗驗證了其預測性能要優于傳統模型.

當前，序列到序列深度學習已廣泛應用于序列數據處理問題，在許多情況下具有出色的性能，尤其是自然語言處理任務[19].序列到序列深度學習模型使用編碼器將輸入序列編碼為固定維數的向量，然后基于該編碼向量進行目標序列解碼作為預測輸出，該方法可以理解為一種通用的序列數據處理端到端框架，備受研究人員的關注.例如Sutskever等人[20]提出了一種通用的端到端序列學習方法，該方法提出了一種觀點，即簡單直接的模型也可以實現有效的機器語言翻譯；Venugopalan等人[21]提出了一種序列到序列模型來生成視頻字幕，該模型相比傳統模型，在圖像字幕生成任務中具有更佳的性能；Kuznetsov等人[22]對基于序列到序列深度學習的時間序列預測框架進行了深入的理論分析，并將序列到序列學習與經典時間序列方法進行了實驗性能比較；Li等人[23]提出了一種基于編碼器解碼器的擴散卷積循環神經網絡(diffusion convolutional recurrent neural network, DCRNN)，該交通流預測深度學習框架能夠學習到深層的時空依賴性特征.

盡管如此，基于序列到序列學習結構的交通流預測模型，還鮮有系統深入的研究.現有的研究方法也很少從時空注意力機制的角度來擴展長時空序列的建模能力，此外，時空序列的多步預測要比單步預測更加困難，而結合注意力機制的序列到序列學習結構有望提升預測性能.與經典的統計分析和機器學習方法不同，本文通過基于時空注意力擴展的序列到序列學習構建模型并應用于交通流的多步預測.實驗結果表明，該模型可以進行有效的多步交通流預測.

2 序列到序列學習

首先對序列到序列學習這種新的深度學習結構進行分析和論述，經典的序列到序列學習模型將可變長時序數據編碼為固定長度的向量表示，然后將學習到的固定長度向量表示進行解碼作為預測輸出.從概率的角度來看，序列到序列模型是一種通用的學習框架，采用其進行城市交通序列建模的本質是學習以一個可變長度序列為條件的另一個序列的條件分布，所以序列到序列學習模型的計算過程可以描述為

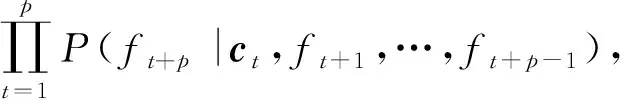
(1)

其中,(Xt-l,Xt-l+1,…,Xt)是作為模型輸入的歷史交通流相關時序數據，(ft+1,ft+2,…,ft+p)是模型的多步預測輸出序列，其長度p(prediction size)為多步預測數，模型輸入時序數據窗口大小為l(lookup size).該模型的編碼器首先對輸入序列(Xt-l,Xt-l+1,…,Xt)進行編碼，生成并構建其隱含的特征表示，即上下文向量ct.模型解碼器在獲取最后一個隱藏狀態輸出之后，可對上下文向量ct進行解碼，然后預測輸出(ft+1,ft+2,…,ft+p).

在實際應用中，編碼器和解碼器可以有多種深度神經網絡供選擇，如編碼器和解碼器都是RNN，接下來分析整個序列到序列學習模型的計算過程.對于可變長輸入序列，在每個時間步t，RNN的隱藏狀態輸出計算為

ht=RNN(ht-1,xt).

(2)

編碼器RNN網絡，順序讀取輸入序列的每個值，同時RNN的隱藏狀態根據式(2)進行改變.讀取到序列結束位置后，RNN的隱藏狀態即為時間步t的編碼器隱藏狀態，其計算為

ht=RNNenc(ht-1,ft-1,ct).

(3)

解碼器RNN網絡，可以通過預測給定隱藏狀態條件下的下一個時間步數值來作為模型的預測輸出，這里需要同時結合上一步預測輸出和編碼后的上下文向量作為輸入.所以解碼器時間步t的隱藏狀態計算為

P(ft|ft-1,ft-2,…,f1,ct)=
RNNdec(ht,ft-1,ct).

(4)

整個序列到序列學習模型的2個組件(編碼器網絡與解碼器網絡)經過聯合訓練，最小化損失函數：

(5)

其中,θ是代表整個時空注意力模型的參數空間，n代表訓練樣本數，λ代表訓練損失函數的正則項參數.

3 序列到序列時空注意力學習模型

3.1 模型總體框架設計

基于經典的序列到序列學習結構進行交通流預測過程，如式(6)所示，模型需學習以可變長度輸入序列為條件的預測序列條件分布，而對交通序列進行編碼和解碼組件之間的唯一聯系是上下文矢量.換句話說，編碼器需要將整個輸入交通序列編碼壓縮表示為固定長度的向量.

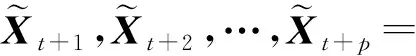
(6)

但是上述直接編碼解碼過程面臨2個問題：1)上下文矢量不能完全表示整個輸入交通序列的深層特征;2)前面輸入序列數據編碼獲取的深度特征有可能被后續的輸入序列編碼特征所覆蓋或沖淡，當輸入序列越長，這個問題就越嚴重.這2個問題使得基于經典序列到序列學習結構的交通流多步預測面臨挑戰，隨著與輸入交通流有關的序列數據長度的增加，多步交通流預測性能會迅速下降.

為了解決上述2個問題，所提出的模型引入了時空注意力機制來處理多步交通流預測任務(如圖3所示)，另外經典的RNN或LSTM只能獲取時間依賴特征，難以獲取多站點序列的空間依賴特征[24]，所以模型設計進一步引入了卷積LSTM作為編碼器組件，來對時空序列數據中的空間依賴特征和時間依賴特征同時進行深度表示和編碼學習.

基于時空注意力編碼器-解碼器結構的交通流預測模型包括3個部分：卷積LSTM編碼網絡、LSTM解碼網絡和時空注意力層,如圖3所示.編碼器從輸入交通流相關的時空序列學習其隱藏特征(包括長時依賴性特征和時空關聯性特征)，并通過上下文生成向量結合時空注意力向量構建歷史交通序列數據的深度潛在時空表示，即注意力上下文向量.LSTM解碼器基于編碼的時空注意力向量進行解碼，以重建交通流序列作為目標預測值.圖3展示了該模型框架的詳細設計圖.

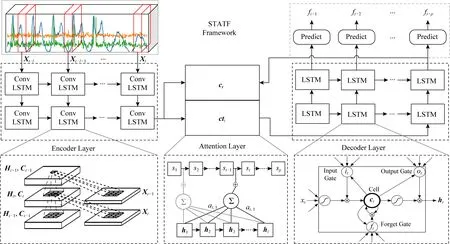
Fig. 3 The diagram of the spatial-temporal attention model for traffic flow prediction (STATF)圖3 基于序列到序列時空注意力的交通流預測模型(STATF)框架圖.

雖然與標準RNN相比，LSTM已被證明是學習時序數據長時依賴特征的最有效模型.但是，與交通流相關的時空序列數據不僅包含時間特征，而且還包含空間分布特征，由于經典的LSTM只能學習到時間依賴特征，難以有效地抽取空間相關性特征，卷積LSTM通過卷積運算代替傳統的乘法計算，可以在一定程度上克服這一問題.所以為了對交通流相關的時序數據中的時空相關特征進行抽取和學習，首先提出卷積LSTM作為序列到序列注意力模型的編碼器組件.卷積LSTM是對經典LSTM的擴展，該模型在LSTM的基礎上用卷積運算代替原來的矩陣乘法運算,如圖4所示.卷積LSTM不僅保留了LSTM可以學習不同時間步的長時依賴性特征的優勢，同時還可以捕獲多序列數據中的空間時空關聯特征.因此，STATF模型使用卷積LSTM作為Encoder組件.

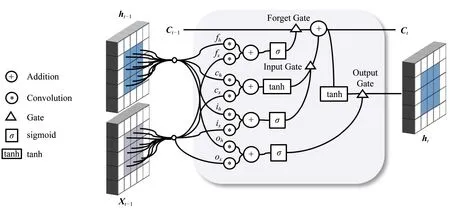
Fig. 4 Diagram of ConvLSTM Cell Block[25]圖4 卷積LSTM單元內部結構示意圖[25]

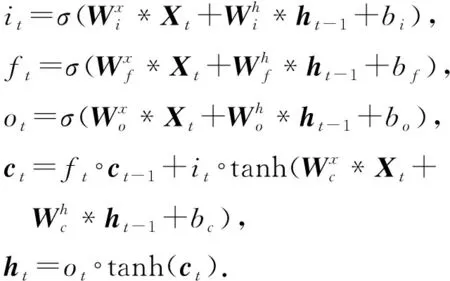
(7)

式(7)定義了卷積LSTM的詳細計算過程，其中*表示卷積運算(卷積LSTM與LSTM的矩陣乘法運算不同，關鍵區別就在于*表示卷積運算而不是矩陣乘法運算)，°表示逐元素乘法，σ表示S型函數.it，ft，ot分別表示t時間步的輸入門，忘記門和輸出門，ct是t時間步的單元輸出，ht是t時間步的單元隱藏狀態輸出，與經典LSTM不同，上述符號表示的都是3D張量.

3.2 時空注意力學習機制

本節介紹基于序列到序列結構的時空注意力機制計算原理及過程，設輸入的交通流序列和預測目標序列分布表示為X={x1,x2,…,xT}和f={f1,f2,…,fp}.卷積LSTM編碼器接受每個時間窗口的時序數據輸入以及上一個時間步的隱藏狀態，輸出ht和ct分別是第t個時間步的隱藏狀態和編碼的上下文潛在向量：

ht,ct=ConvLSTMenc(xt,ht-1,ct-1),

(8)

(9)

如式(9)所示，cti是模型構建的時空注意力向量，由卷積LSTM編碼器輸出的隱藏狀態求加權平均值獲得，其中每個編碼器的隱藏狀態相對應的權重計算如下：

(10)

其中,eij是一個得分函數，通過使用LSTM解碼器的隱藏輸出狀態和卷積LSTM編碼器的隱藏狀態來計算得分：

(11)

模型中的LSTM解碼器基于編碼的上下文潛在向量，結合上一個時間步接受的目標序列輸出和隱藏狀態輸出進行解碼計算：

st=LSTMdec(ft-1,st-1,ct-1).

(12)

最后，對時空注意向量cti與LSTM解碼器的隱藏狀態輸出st進行連接計算，通過一個全連接網絡層計算作為預測輸出：

(13)

通過上述計算過程，結合梯度下降策略來訓練所提出的模型，可以最大程度地減少預測交通流量值和真實交通流量值之間的誤差，逐步降低模型的損失函數值，從而得到更優的預測結果，損失函數計算如式(5).整個模型訓練過程的偽代碼描述如算法1.

算法1.STATF模型訓練過程.

輸入:交通流相關的多變量時空序列數據集{xi,j|i=1,2…,n;j=t-l,…,t-1}、輸入窗口l、前向預測步p;

輸出:訓練好的STATF模型.

①Dtrain←?;

② 根據輸入數據構建訓練集Dtrain=(X,Y);

/*訓練模型*/

③ 初始化STATF模型的參數空間θ;

④ repeat

⑤ 從訓練集Dtrain中選擇批處理樣本Db;

/*基于深度注意力編碼的交通流序列表示學習*/

⑥ht,ct=ConvLSTMenc(xt,ht-1,ct-1);

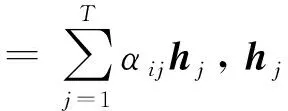
⑧st=LSTMdec(ft-1,st-1,ct-1);

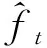
⑩ 最小化目標函數(式(5))獲得最優參數空間θ;

算法1描述了STATF模型的訓練過程，首先從輸入的交通序列數據中構建訓練實例樣本，然后通過反向傳播和Adam優化器對模型進行逐批次迭代訓練.通過上述序列到序列的時空注意力計算過程可以獲取并學習歷史交通流時空序列數據中的深層時空關聯特征，從而提升模型的多步交通流預測性能.接下來進一步對該模型進行實驗評估和分析.

4 實驗設置與結果分析

為了測試所提出模型的性能，基于3個真實的城市交通數據集進行實驗.通過與經典的淺層學習模型和基準深度學習模型(包括最新提出的交通預測模型)對比，驗證了該模型的交通流預測性能和有效性.

4.1 數據集

第1個數據集來源于英國政府開發數據平臺，簡稱為Highway England Dataset[26]，該平臺發布有關英格蘭的2類主要公路網的交通流數據信息，所有主干戰略高速公路網絡和本地化的公路網.Highway England交通流數據集是一個典型的多變量時空序列，該數據集采集了每間隔15 min的平均通行時間，通行速度和交通流量等信息，實驗所用的數據集時間跨度為2013-01-01—2014-02-31.第2個實驗數據集簡稱為PEMS-BAY[27]，該交通數據集來源于美國加利福尼亞州運輸部門的PeMS系統，實驗選擇了在灣區的325個傳感器采集點數據，一共收集了5個月的數據，時間范圍跨度為2017-01-01—2017-05-31，圖5顯示了該數據集的采集點位置分布.第3個實驗數據集簡稱為METR-LA[23]，該數據集來源于洛杉磯高速公路網的交通流采集設備，實驗選擇了其中207個傳感器采集的數據，時間跨度范圍為2012-03-01—2012-06-30的4個月數據.

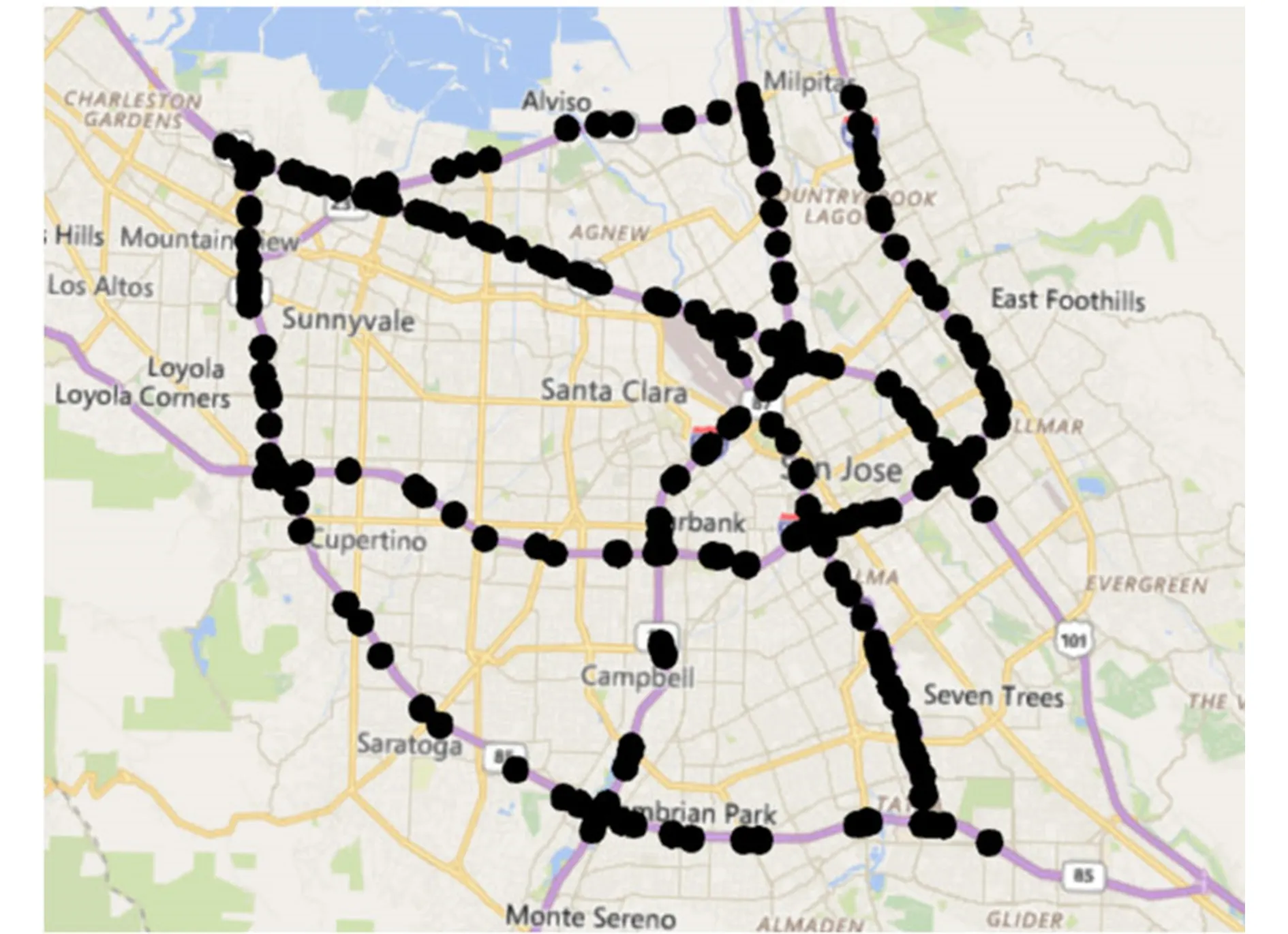
Fig. 5 Sensor distribution of the PEMS-BAY dataset[23]圖5 PEMS-BAY數據集的采集點位置分布圖[23]

4.2 基準對比模型與超參數設置

本節描述實驗的硬件和軟件環境以及相關模型參數的配置情況，首先基于Tensorflow為Backend的開源深度學習庫Keras，來構建各類深度學習實驗模型，包括提出的STATF模型，采用Scikit-learn機器學習庫用于構建基準對比淺層學習模型.所有實驗均在PC服務器上進行，該服務器配置為Intel?Xeon?CPU E5-2623 3.00GHz，4個GPU每個配置為12 G NVIDIA Tesla K80C，內存為128 GB.另外，為了驗證模型的預測效果，將STATF模型與以下8個基準模型進行比較：

1) VAR.向量自回歸模型可以對多變量時間序列數據之間的隱含關系進行建模，可以把VAR模型看做是集合多元線性回歸的優點(可以加入多個因子)以及時間序列模型的優點(可以分析滯后項的影響)的綜合模型.

2) ARIMA.自回歸綜合移動平均值法是一種廣泛用于時間序列分析的模型，它結合了移動平均值和自回歸方法.

3) SVR.支持向量回歸是支持向量機模型的一種變體方法，經常用于時間序列預測，一般使用3種不同核函數(RBF，POLY和LINEAR)的SVR模型.

4) RNN.這是用于處理序列任務的最為傳統的深度學習方法，LSTM和GRU(門控循環單位)是2種最流行的基于RNN變體的深度學習模型.

5) ConvLSTM[16].經典的卷積LSTM網絡，采用其作為城市交通流量預測實驗的基準模型.

6) SEQ2SEQ[20].經典的序列到序列深度學習網絡，編碼器解碼器都為LSTM，不包含注意力網絡層，SEQ2SEQ可以視為STATF模型的一種簡單變體.

7) SAE[10].Lv等人提出的一種基于深度堆疊自編碼器(Stacked Auto-encoder)框架的交通流預測模型.

8) DCRNN[23].Li等人提出了一種基于編碼器解碼器的擴散卷積循環神經網絡(DCRNN)，該深度學習框架能夠學習到交通流數據中的時空依賴性特征.

STATF模型訓練過程中的參數設置情況如下，首先選擇均方誤差(MSE)作為模型訓練的損失函數，交通流建模的訓練集和測試集分割策略為：數據集的前70%作為模型訓練集，剩余30%作為測試集.此外，采用了min-max函數將交通流相關序列數據都標準化到[0,1]區間.基準深度學習模型和STATF模型的基礎超參數配置一樣，具體配置為：訓練迭代次數為100，批處理大小為96，每層的神經元丟棄率為0.3，學習率參數為0.01，基準深度學習模型的默認神經網絡層數設置為1，每個隱藏層神經元數量為100，所有深度學習模型均采用Adam函數用作模型訓練優化器.卷積LSTM的filters和kernels參數大小分別設置為64和(1,5)，解碼器的LSTM網絡每層神經元數量也設置為100.模型輸出層的激活函數采用linear線性函數，用于最終預測.最后，將RMSE和MAE作為模型誤差分析指標，用于評估各個模型的預測性能，誤差指標計算公式為：

(14)

(15)

4.3 實驗結果分析

基于3個真實的交通流數據集進行實驗分析和評估，在實驗過程中對STATF模型與其他對比模型的總體預測性能進行比較.實驗對比結果如表1所示，其中給出了STATF模型與對比模型從t+1到t+12的未來12個時間步內的多步交通流預測平均誤差RMSE和MAE結果，包括經典的淺層學習模型VAR，ARIMA，SVR和基準深度學習模型RNN，LSTM，GRU等，以及針對交通流預測任務而設計的如SAE[10]和DCRNN[23]深度學習模型.從表1可知STATF模型在多步交通流量預測性能方面要優于其他對比模型.與經典淺層學習和基準深度學習模型相比，STATF模型在未來12個時間步從t+1到t+12的預測都能保持最低的RMSE和MAE平均預測誤差，在一定程度上提升了多步交通流預測的準確性.此外，實驗結果還表明，基準深度學習模型，例如LSTM，GRU的預測性能要明顯優于傳統的淺層學習方法.這是因為與淺層學習模型相比，深度神經網絡結構可以學習到時空序列數據中更為復雜的模式和特征.而相比簡單的變體模型，如SEQ2SEQ與ConvLSTM和針對交通流預測而設計的新型深度學習模型，如SAE與DCRNN，STATF模型更進一步降低了模型的預測誤差.

在多個數據集總體平均預測誤差對比基礎上，繼續對單個數據集的多步預測性能進行比較分析.首先基于Highway England交通流數據集進行實驗分析和評估，實驗對比結果如表2所示，其中給出了STATF模型與基準模型的多個特定時間步t+1，t+3，t+6，t+12的交通流預測誤差RMSE和MAE結果.從表2可知，STATF模型在多步交通流量預測性能方面要優于其他基準對比模型.與基準淺層學習和深度學習模型相比，STATF模型不管是在預測時間步大小為3(t+3)還是預測時間步大小為12(t+12)時，都能保持最低的RMSE和MAE預測誤差.此外，實驗結果還表明，基準深度學習模型，例如LSTM，GRU的預測性能要明顯優于傳統的淺層學習方法，尤其是在長時間步預測的情況下.而相比基準方法和針對交通流預測而設計的深度學習對比模型，如SAE與DCRNN，以及相比如SEQ2SEQ不含注意力機制的簡單變體模型，STATF模型能夠從多個深度網絡的分層結構中提取不同級別的時空表示特征，提升了模型的多步預測性能.

通過實驗結果分析，進一步發現預測時間步長的選擇對模型的預測性能有很大影響.如表2所示，長時間步條件下模型的預測性能，要明顯低于短時間步長預測的性能.產生這種現象的原因是，模型每個時間步的預測都需要考慮前一個時間步長的預測結果，這種情況下隨著預測時間步長的增加，前面時間步的模型預測誤差會逐步累積，從而使得整個模型的預測誤差越來越大.這也符合人們的直觀認知.所以，隨著預測時間步長的增加，每個實驗對比模型的預測性能都在逐漸下降.但從實驗結果中可以看到，與基準的深度模型和淺層模型相比，在不同的預測時間步長條件下，STATF模型都能保持最低的預測誤差.

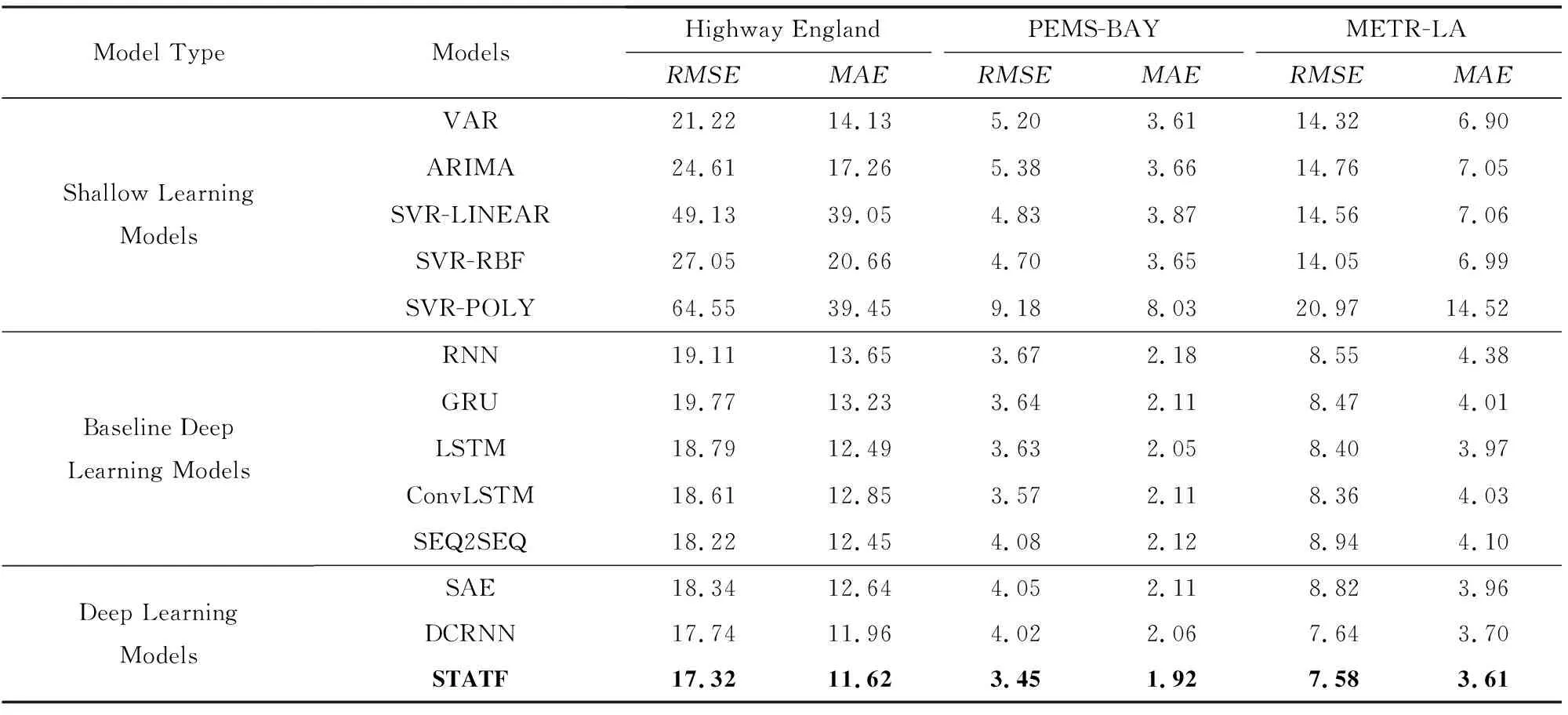
Table 1 Comparison of the Average Prediction Error of Different Models表1 不同模型的平均預測誤差對比

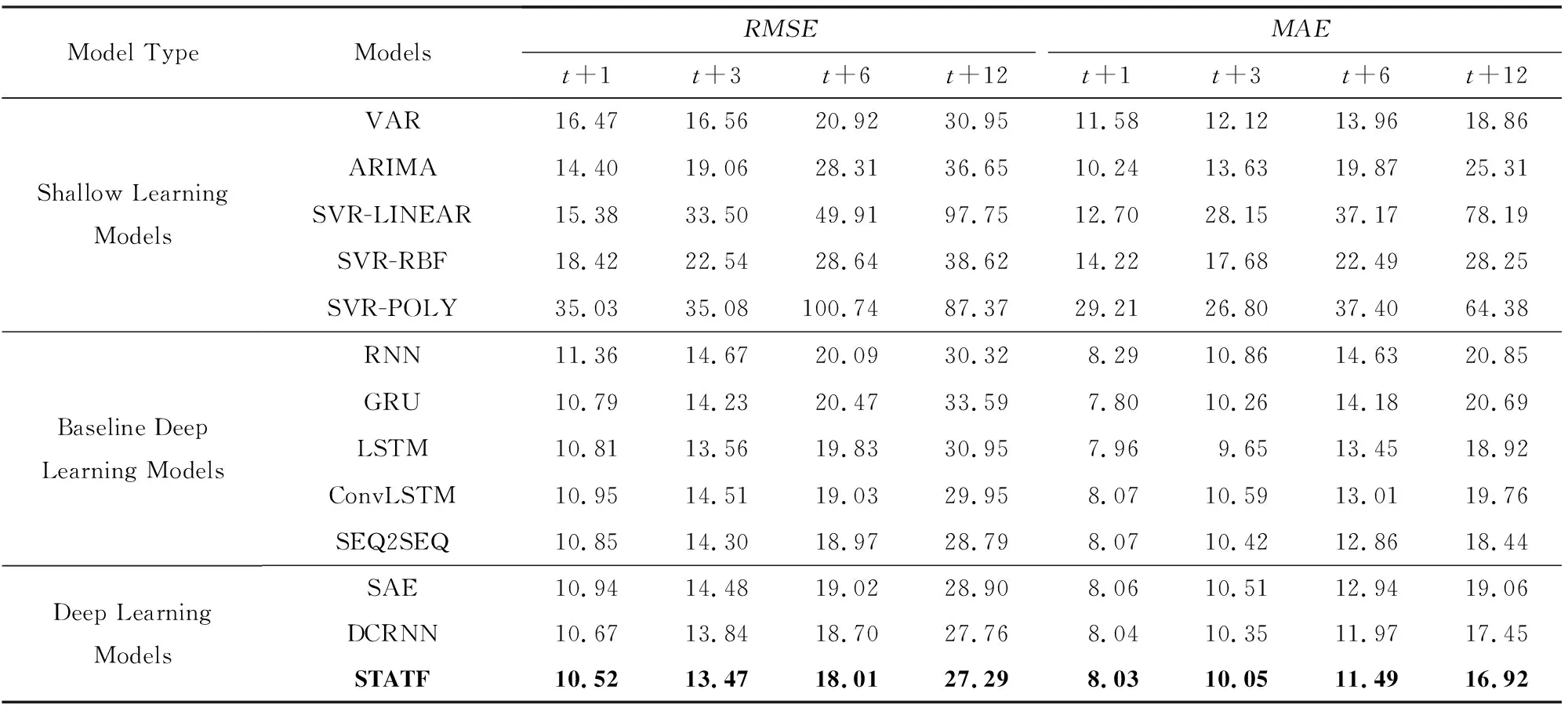
Table 2 Comparison of the Prediction Error of Different Models表2 不同模型的預測誤差對比

為了進一步比較STATF模型和其他基準模型在不同時間步長條件下的預測性能，分析并顯示了不同模型在一個工作日內(包括96個時間步，每個時間步間隔15 min)、在不同預測時間步長大小條件下的交通流量預測性能，以及一周內(包括672個時間步、每個時間步間隔同樣是15 min)的比較情況.如圖6和圖7所示，分別為一個工作日(2013-11-18)和一周(2013-11-18—2013-11-24)的預測情況，比較SVR-RBF，RNN和本文提出的STATF模型的實際觀察到的交通流量值和預測交通流量值對比曲線，其中x坐標表示觀測時間步長，y坐標表示該時間步的交通流量值.從2個曲線對比圖可以看到，不管是一個工作日內還是拉長到一周時間范圍內，STATF模型的預測性能都要優于以SVR-RBF為代表的淺層模型和以RNN為代表的深度學習模型.還有就是不管是在工作日情況下，還是在周末情況下，如圖7最后2個波峰，特別是在交通流波峰和波谷時間范圍內的預測情況，STATF模型預測性能都能保持最優.另外，2個圖示分析都表明：RNN模型的預測性能要優于SVR-RBF模型，隨著預測時間步長的增加，淺層學習模型的預測性能會顯著下降，而STATF模型和基準深度學習模型可以保持良好穩定的性能.上述實驗結果分析表明，在不同的時間步長預測條件下，STATF模型在Highway England數據集上的多步預測性能要優于基準淺層學習模型和深度學習模型.

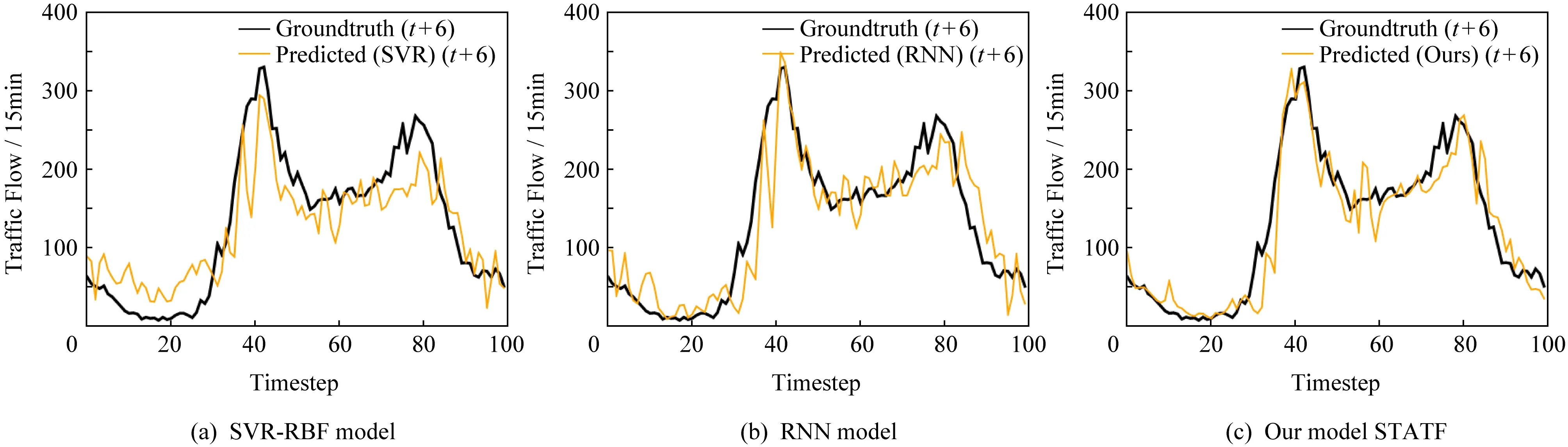
Fig. 6 Comparison of ground truth value and predicted traffic value of different models during one day圖6 不同模型在一個工作日內的交通流預測值與真實值對比

Fig. 7 Comparison of ground truth value and predicted traffic value of different models during one week圖7 不同模型在一周內的交通流預測值與真實值對比

繼續對PEMS-BAY數據集進行各模型的多步預測性能比較.在實驗過程中對STATF模型與其他基準模型、當前最優模型等的預測性能進行比較，實驗對比結果如表3所示，其中給出了STATF模型與基準模型的多個時間步下的交通流預測誤差結果.從表3可知，在PEMS-BAY數據集實驗中，無論預測時間步長是多少，STATF模型的預測性能同樣都比其他基準模型要好，即使對于未來12個小時后的長時間步預測，STATF模型預測性能也是所有對比模型中最好的.具體到RMSE與MAE誤差指標值，與基準淺層學習模型和深度學習模型相比，當預測時間步大小為3時，STATF模型的RMSE和MAE值分別為3.04和1.72，預測誤差值最小；當預測時間步長為12時，STATF模型的RMSE和MAE值分別為4.81和2.52，預測誤差值同樣能保持最低.

另外，基準深度學習模型(例如LSTM，GRU和ConvLSTM)的預測性能同樣明顯優于傳統的淺層學習方法，特別是在長時間步預測的情況下.傳統的時間序列預測方法(例如VAR和SVR)在交通流預測任務上難以獲得與深度學習模型一樣的性能，是因為它們僅僅依賴于交通流歷史記錄本身來預測未來值，而與交通流相關的其他城市時空序列數據難以一起建模，所以傳統模型方法無法捕獲與交通流相關的城市時空序列數據中的隱藏長時依賴特征和非線性時空關聯關系.STATF模型可以在一定程度上降低上述問題的影響，因此在與其他基準深度學習模型、及當前最優深度學習模型等(如SAE模型[10]與DCRNN模型[23])的實驗對比中能具有最佳的預測性能.

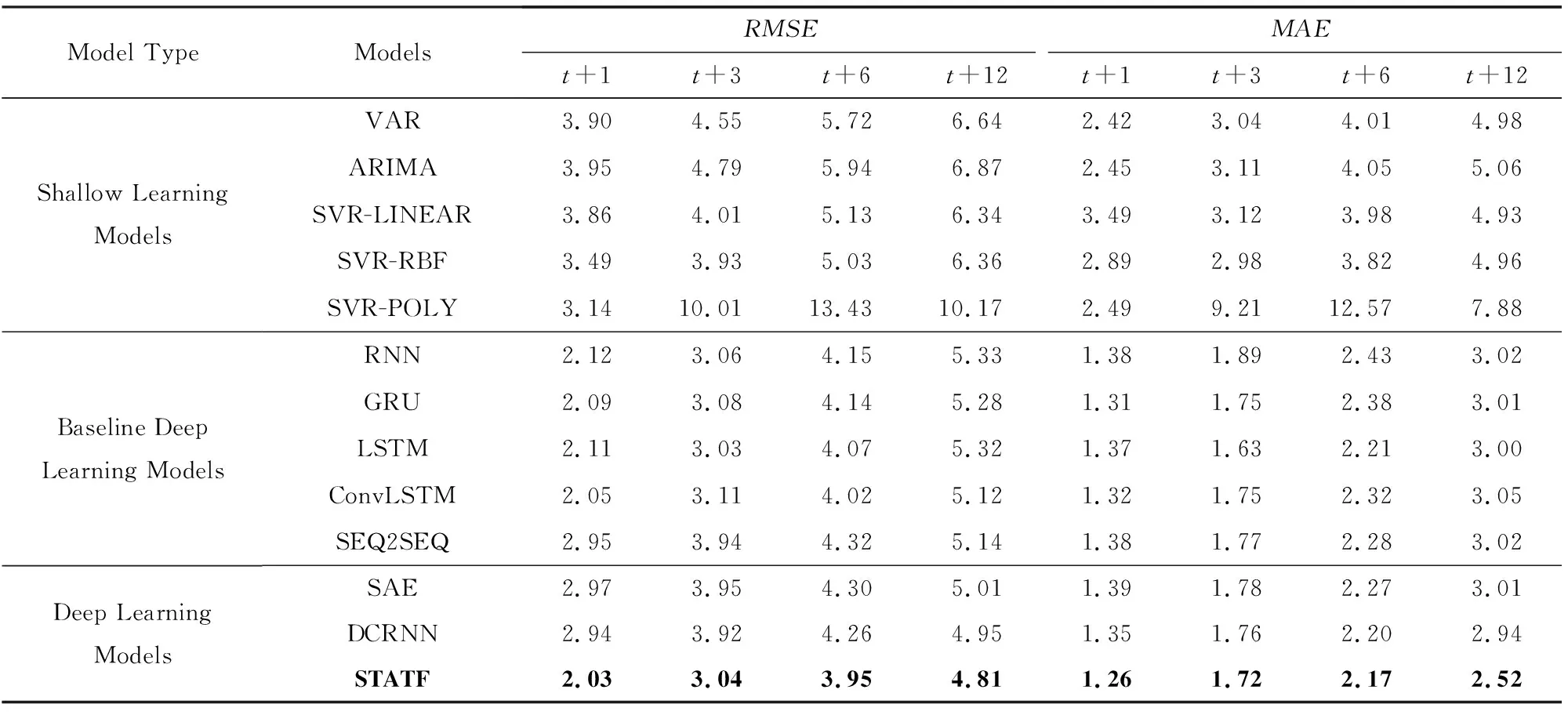
Table 3 Comparison of Traffic Flow Prediction Error Indexes of Different Models表3 不同模型的交通流多步預測誤差指標對比

為了進一步分析和比較STATF模型與基準方法在PEMS-BAY數據集上的預測表現，如圖8所示，其中水平軸表示觀測的時間步長，垂直軸代表交通序列值，該圖展示了SVR-RBF，RNN，STATF模型在單步預測t+1和多步預測t+6條件下的交通流預測誤差情況.從圖8中可以看到，STATF模型在不同時間步預測情況下都能保持最優的預測性能，圖8中預測值曲線與真實值曲線能夠很好的匹配.STATF模型的預測性能，不管是在波峰還是波谷時段，都要優于以SVR-RBF為代表的淺層模型和RNN為代表的基準深度學習模型.另外，隨著預測時間步長的增加，SVR-RBF模型和RNN模型的預測性能在急劇下降，但STATF模型的預測性能下降趨勢要比SVR和RNN模型更為緩慢，可以相對較好地保持更優的交通流預測準確性.不同深度學習模型在單步預測條件下性能差異較小，而在長時間步預測情況下，STATF模型的性能優勢更為明顯.

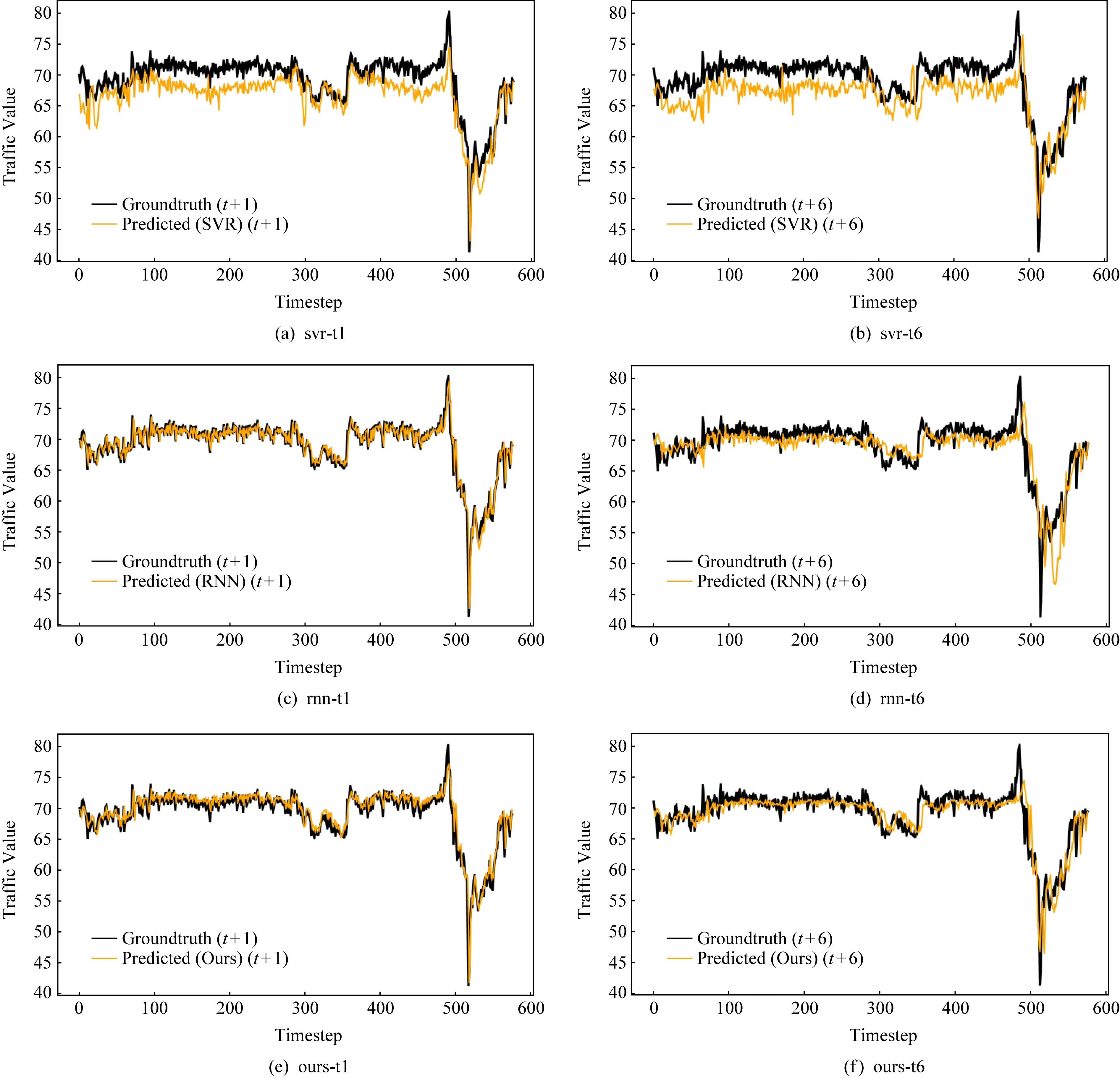
Fig. 8 Comparison of ground truth value and different time-step (t+1 and t+6) predicted traffic value of different models圖8 不同模型在t+1和t+6時間步下的交通流預測值與真實值對比

最后，為了分析多個時序特征相比單序列特征對交通流建模的影響，對STATF模型在不同數據集上的單變量預測和多變量預測性能進行了對比.表4的結果給出了STATF模型在3個交通流數據集下的對比實驗結果，包括在單變量時序輸入條件(unvariate)和多變量時間序列輸入條件(multivariate)下的預測誤差值RMSE與MAE.以Highway England數據集為例，在單變量輸入條件下，僅將traffic flow單變量序列輸入模型；而在多變量時間序列輸入條件下，則將traffic flow變量本身和其他變量一起輸入模型,例如通行速度speed、通行時長pass time等.如表4所示，與單變量輸入條件下的預測誤差相比，多變量時間序列輸入條件下的模型預測誤差有一定程度降低，這表明STATF模型可以有效學習多元交通流序列數據中非線性相關性特征.

綜上所述，通過在3個真實交通流數據集上進行的實驗結果分析，所提出的基于序列到序列時空注意力深度學習的交通流量預測模型STATF，相比基準模型和當前最新提出的模型，具有更好的預測性能.不管是在單步預測還是在長時多步預測條件下，STATF模型的交通流預測值都可以與真實值保持較好的匹配.同時，在各種時間步長預測條件下，該模型的預測誤差也比基準模型更低.這驗證了STATF交通流預測模型的性能，可以有效地學習多變量交通流相關時空序列數據中的深層非線性相關特征和時空依賴特征.

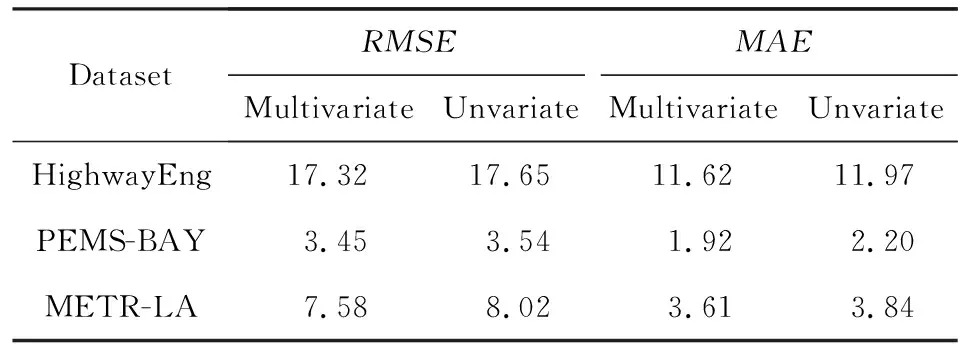
Table 4 Comparison of Unvariate and Multivariate Prediction Error of Different Models on Three Datasets表4 STATF模型在3個數據集上的單變量預測與多變量預測誤差指標對比

5 總 結

針對交通流預測面臨的兩大關鍵挑戰性問題，提出了一種新的交通時空序列端到端深度學習框架，該模型將序列到序列深度學習結構、卷積LSTM網絡和時空注意力機制進行模型集成，并對模型的核心框架設計與時空注意力機制原理過程等進行了詳細分析和論述.所提出的STATF模型不僅考慮了交通流相關數據中的時空相關性特征，而且還能捕獲與交通流有關的多變量城市時空序列中的非線性相關性特征.在3個真實交通流數據集上進行的實驗結果表明，STATF模型相比經典淺層學習模型、基準深度學習模型、以及當前新提出的2種交通流深度學習模型，具有更優的預測性能，驗證了該模型可以探索和學習到多變量交通序列數據中的隱含時空依賴性特征和非線性相關特征.

未來的主要工作是收集有關交通事故或極端天氣事件的數據，進一步對該模型進行深入研究和改進，實現對未來的長時多步城市交通流量，尤其是在交通事故或極端天氣等突發情況下的有效預測，以及適應其他更復雜的交通流預測情況.