一種三參數(shù)統(tǒng)一化動量方法及其最優(yōu)收斂速率

丁成誠 陶 蔚 陶 卿

1(中國人民解放軍陸軍炮兵防空兵學(xué)院信息工程系 合肥 230031)2(中國人民解放軍陸軍工程大學(xué)指揮控制工程學(xué)院 南京 210007)(dcc18851507462@163.com)

無論是經(jīng)典的正則化損失函數(shù)框架,如稀疏學(xué)習(xí)和支持向量機,還是當(dāng)前的研究熱點深度學(xué)習(xí),如卷積和遞歸神經(jīng)網(wǎng)絡(luò),都可以視為給定模型空間的參數(shù)尋優(yōu)問題,隨機梯度下降法(stochastic gradient descent, SGD)是解決這類參數(shù)尋優(yōu)問題簡單而又有效的方法.為了獲得更好的收斂性能,人們開始在SGD的基礎(chǔ)上使用動量方法.

動量實際上是物理學(xué)中的一個概念,動量原理告訴我們運動的物體會因為慣性繼續(xù)保持運動,除非受到外力作用而停下來.在優(yōu)化算法中,動量方法可以在梯度很小的情形下仍然保持更新,從而可以加速SGD在求解凸優(yōu)化問題時的收斂速率[1-3],幫助SGD在求解非凸優(yōu)化問題時擺脫局部最優(yōu)點[4-5].對于隨機優(yōu)化問題,由于動量可以分解成過往梯度加權(quán)平均的方式,因此比SGD具有更小的方差,據(jù)此使算法獲得了更好的收斂性和穩(wěn)定性[6].

我們通常討論的動量方法有2種標準形式：一種是由Polyak于1964年提出HB(heavy ball)方法[7]；另一種是Nesterov于1983年提出的NAG(Nesterov’s accelerated gradient)方法[8].HB的加速性主要體現(xiàn)在目標函數(shù)強凸且二次可微時,盡管與梯度下降法、NAG具有相同的線性收斂速率,但HB具有最小的收斂因子.NAG的加速性主要體現(xiàn)在求解凸光滑目標函數(shù)時,可以將梯度下降法的收斂速率加速至最優(yōu)O(1t2),其中t是迭代步數(shù).對于非光滑凸優(yōu)化問題,SGD，HB和NAG具有相同的最優(yōu)平均收斂速率,但對于個體收斂性,HB和NAG也具有加速效果,可將SGD的個體收斂速率從O(log加速至最優(yōu)的[1-2].

在深度神經(jīng)網(wǎng)絡(luò)訓(xùn)練中,使用動量優(yōu)化方法替代無法選取合適步長的SGD,已經(jīng)在計算機視覺等方面取得了很好的效果[9].Ochs等人通過實驗驗證了批處理形式的HB方法能夠逃離局部最小值點[4].2019年Sun等人從理論上證明了HB方法比GD方法有更大的步長從而可以逃避鞍點[5].而NAG也表現(xiàn)不凡,可以提高RNN在許多任務(wù)中的性能[10].

目前,人們已經(jīng)將典型的動量優(yōu)化方法寫進了深度學(xué)習(xí)的優(yōu)化器中.隨著優(yōu)化方法進一步發(fā)展,出現(xiàn)了眾多形式的動量方法.典型的有2016年Lessard等人提出的SNV(synthesized Nesterov variants)[11]、2018年Kidambi等人的AccSGD(accelerated SGD)[12]、Bryan等人的Triple動量方法[13]以及Cyrus等人提出的Robust動量方法[14]等等.

綜上,無論是從理論分析還是從理解動量在優(yōu)化算法中作用的角度來看,建立一個統(tǒng)一的動量方法的一般框架都是十分必要的.實際上,早在2013年,Sutskever等人就發(fā)現(xiàn)HB方法和NAG方法的區(qū)別僅僅在于計算梯度的點選取不同[15]；通過引入中間變量,Yang等人于2016年提出了一種隨機統(tǒng)一化動量方法(stochastic unified momentum, SUM),統(tǒng)一了SGD，HB和NAG[16];2019年Ma等人提出了QHM(quasi-hyperbolic momentum)方法,其迭代步驟可以表示成SGD與動量緩沖項的一種加權(quán)平均方式.QHM通過使用動量緩沖和加權(quán)SGD的2個折中參數(shù)將AccSGD，Triple，Robust等形式的動量方法進行統(tǒng)一[6].顯然,SUM和QHM在統(tǒng)一化動量方法上的思路是不同的.

動量方法在有效提高SGD收斂性能的同時,也存在一些令人質(zhì)疑的地方,即由于動量改變了SGD中梯度下降的操作,是否還能保持SGD原有的收斂性能?具體來說,對于非光滑凸問題,我們首先應(yīng)該證明動量方法具有和SGD一樣的最優(yōu)平均收斂速率.但遺憾的是目前的研究還存在一些欠缺.特別地,對于非光滑凸目標函數(shù),盡管SUM得到了最優(yōu)的O(1t)平均收斂速率[16],但其使用的步長嚴重依賴預(yù)先設(shè)定的迭代步數(shù),這種固定總迭代步數(shù)的方法在處理大規(guī)模數(shù)據(jù)時由于不能增量地執(zhí)行算法而缺少實用性.另一方面,QHM雖然在實驗中的性能超越了HB和NAG,但只討論了光滑情況下的收斂性,也沒有給出具體的收斂速率[6,17].除此以外,這些方法均只適用于無約束情況,不能用于解決機器學(xué)習(xí)中如稀疏學(xué)習(xí)導(dǎo)致的有約束問題.據(jù)我們所知,目前還沒有文獻涉及詳細分析動量方法在有約束非光滑情況下的平均收斂性問題.

本文的貢獻主要體現(xiàn)在3個方面:

1) 提出了一種含三參數(shù)的統(tǒng)一化動量方法TPUM(triple-parameters unified momentum),通過取不同的參數(shù),能夠同時包含SUM和QHM,是目前最一般的動量算法的統(tǒng)一框架.

2) 即使是對特例QHM,本文也給出約束非光滑情形的最優(yōu)平均速率,而QHM目前只有光滑情形下的收斂性結(jié)論.即使是對特例SUM,本文也去掉了SUM原有收斂性中需要固定迭代步數(shù)和無約束等不合理限制.

3) 證明了所提出的TPUM方法在求解有約束非光滑凸優(yōu)化問題時具有最優(yōu)的平均收斂速率,并將其推廣到隨機情況,從而保證了添加動量不會影響標準梯度下降法的收斂性能以及動量方法對機器學(xué)習(xí)問題的可應(yīng)用性.

1 TPUM方法

考慮優(yōu)化問題:

minf(x), s.t.x∈Q,

(1)

批處理形式的投影次梯度方法的迭代步驟為

(2)

f(xt)-f(x*),

其中，t是總迭代次數(shù),x*是最優(yōu)解.平均輸出收斂速率的數(shù)學(xué)表達式為

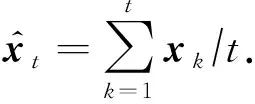
HB更新為

(3)

其中，αk≥0為步長,β∈[0,1)為動量xk-xk-1的系數(shù).

NAG更新為

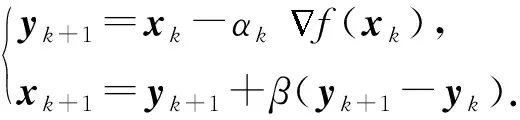
NAG等價于:

(5)

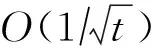
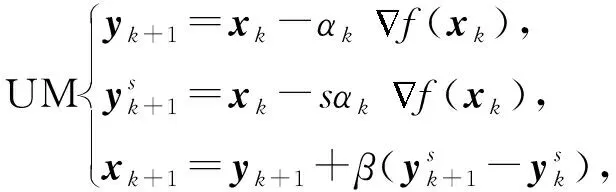
其中，s≥0為一常數(shù),不同的s對應(yīng)不同動量方法.

QHM更新如下:

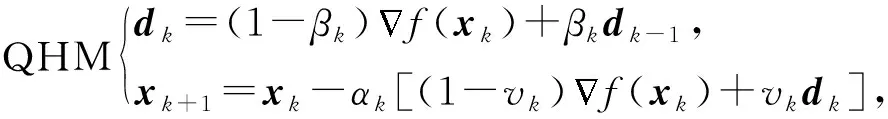
其中，dk稱為動量緩沖器.顯然,QHM也是使用當(dāng)前梯度與過去梯度的凸組合,但由于折中參數(shù)vk，βk的存在,破壞了更容易理解的動量項形式β(xk-xk-1),與SUM統(tǒng)一動量的出發(fā)點是不同的.

然而,通過對文獻[17]的研究發(fā)現(xiàn),動量緩沖器與動量項β(xk-xk-1)具有密切聯(lián)系,可以推出-αβkdk-1=β(xk-xk-1).正是基于這種聯(lián)系,受SUM統(tǒng)一思路的啟發(fā),本文增加2個折中參數(shù)δ1，δ2,將QHM和SUM進行統(tǒng)一,提出TPUM方法:

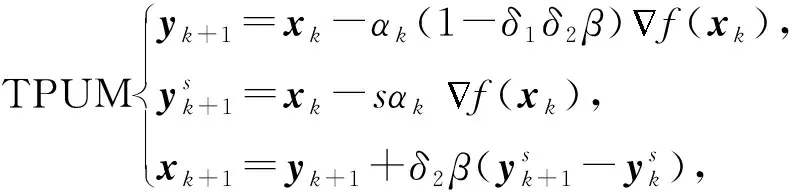
其中,步長αk>0,β∈[0,1)為動量系數(shù),δ1,δ2∈[0,1]為折中參數(shù).顯然:

當(dāng)δ1=0，s=0，δ2=1時,TPUM為HB;

當(dāng)δ1=0，s=1，δ2=1時,TPUM為NAG;

當(dāng)δ1=0，δ2=0時,TPUM為梯度下降法;

當(dāng)δ1=1，s=0，δ2≠0，δ2≠1時,TPUM為QHM.

由此可見,TPUM是目前最一般的動量算法的統(tǒng)一框架.

2 TPUM方法平均收斂性分析

對于有約束問題(1),TPUM更新式(8)可以等價寫成:

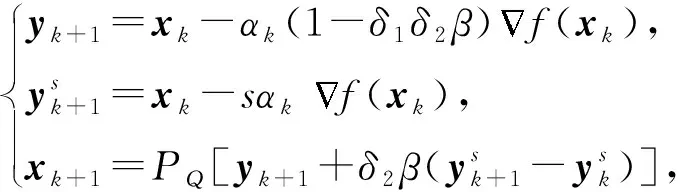
其中,P是Q上的投影算子.式(9)等價于:

(10)

在無約束情況下,文獻[16]中定義:

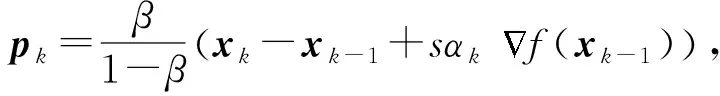
一個直接的優(yōu)勢就是利用式(11)得到:

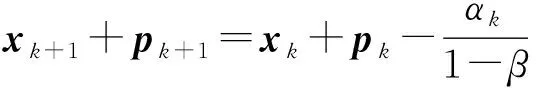
(12)

與已知的梯度優(yōu)化方法十分相像[18],由式(12)出發(fā)很容易得到收斂性結(jié)論,也這正是SUM的主要證明思路.然而,這種方法僅對無約束有效,且使用的是固定步長,對于有約束情況的證明將十分困難.

為此,區(qū)別于式(11),修改動量項，得到:

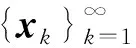
pk=b(xk-xk-1),

其中，b為一個正常數(shù),則

xk+pk=xk+b(xk-xk-1)，
xk+1+pk+1=xk+1+b(xk+1-xk)，
x-(xk+1+pk+1)=x-(b+1)xk+1+bxk，
x-(xk+pk)=x-(b+1)xk+bxk-1.

引理2[19].對于任意x∈RN,x0∈Q:

x-x0,y-x0≤0

當(dāng)且僅當(dāng)x0=P(x)時,對所有的y∈Q恒成立.

實際上,利用約束與投影的關(guān)系,與文獻[18]類似，式(10)中的投影運算可以重新定義為一個優(yōu)化問題:

引理3.式(10)等價于:

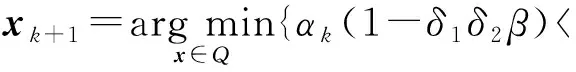
(13)

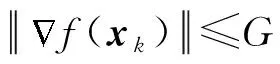
基于上述3條引理及假設(shè)1,可以得到:

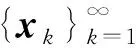
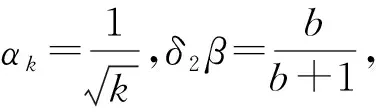
對任意的x∈Q,s≥0,δ1≥0,則

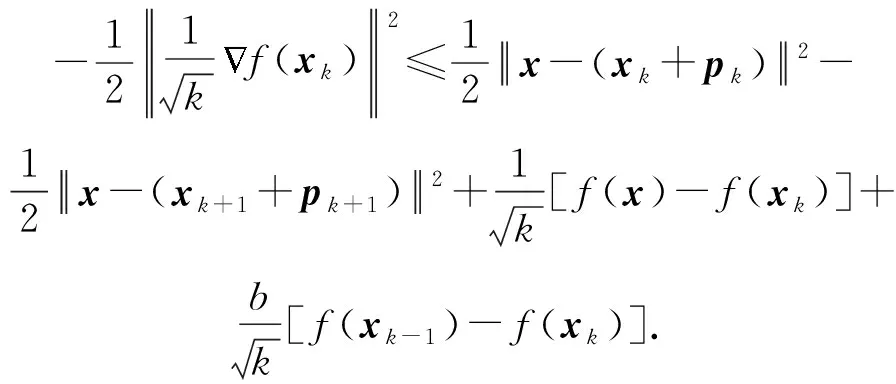
具體證明見附錄A.

通過重新定義的動量項和上述引理,利用凸函數(shù)的性質(zhì),Fenchel-Young不等式,可以得到:

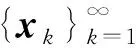
且對任意t>0,

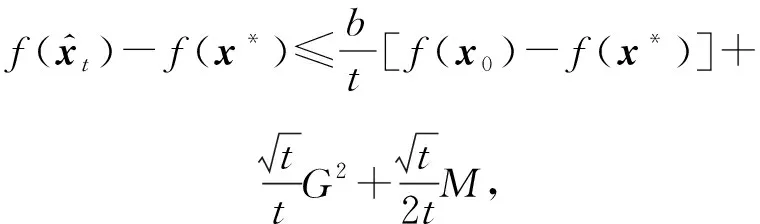
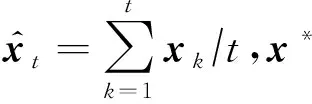
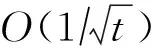
從定理1中可以看出：

1) TPUM是更為一般的統(tǒng)一化動量方法,在非光滑約束情況下可以得到最優(yōu)的平均收斂速率,相比特殊情形的SUM與QHM,TPUM克服了固定步長及無約束的缺陷.

2) 如果使用固定的步長,TPUM將與SUM的證明一樣簡潔,并且同樣可以得到最優(yōu)收斂速率.

3) 文獻[1]證明了在非光滑情形下HB型動量對SGD的個體收斂性具有加速作用,但其證明主要是針對無約束情形,且要求動量系數(shù)是時變的.本文雖然只是得到較弱的平均收斂性,但針對的是有約束問題且考慮的是更一般的統(tǒng)一化動量方法.

優(yōu)化目標函數(shù)為

(16)

其中i為迭代到第t步時隨機抽取的樣本序號.

對于式(10),TPUM的隨機形式迭代步驟為

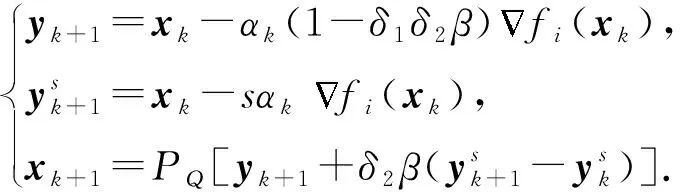
(18)

算法1.隨機TPUM算法.

輸入:循環(huán)次數(shù)t;

輸出:xt.

① 初始化x1=0,設(shè)定α1,δ1,δ2,s,b;

② Fork=1 tot;

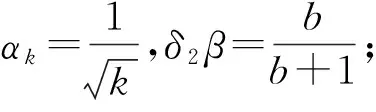
④ 隨機選取i∈{1,2,…,m};

⑥ 由式(17)計算xk+1;

⑦ End For

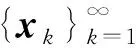
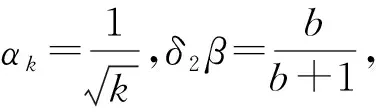
s≥0,δ1≥0,則存在一個正數(shù)M,使得

且對任意t>0,

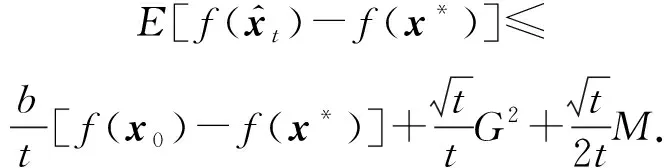
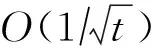
3 實 驗

3.1 實驗?zāi)康?/h3>

本節(jié)通過求解優(yōu)化問題式(16),對隨機TPUM式(17)平均收斂速率的理論分析結(jié)果進行實驗驗證.

主要實驗?zāi)康挠?方面:

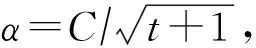
2) 為了驗證所提出的TPUM具有最優(yōu)平均收斂速率,引入DA(dual averaging)算法[22]與TPUM框架下的SHB，SNAG和QHM進行對比,同時在6個數(shù)據(jù)集中各任取了一組超參數(shù)作為TPUM.DA是一種求解非光滑約束問題的經(jīng)典一階優(yōu)化方法[22],具有最優(yōu)的平均收斂速率,因此實驗選取DA作為基準方法，其參數(shù)選擇參照文獻[22]的定理3.

3.2 實驗數(shù)據(jù)集與方法

實驗采用的是6個常用的標準數(shù)據(jù)集,這些數(shù)據(jù)集可以在LIBSVM(1)http://www.csie.ntu.edu.tw/～cjlin/libsvm/網(wǎng)站中找到,詳細描述如表1所示:

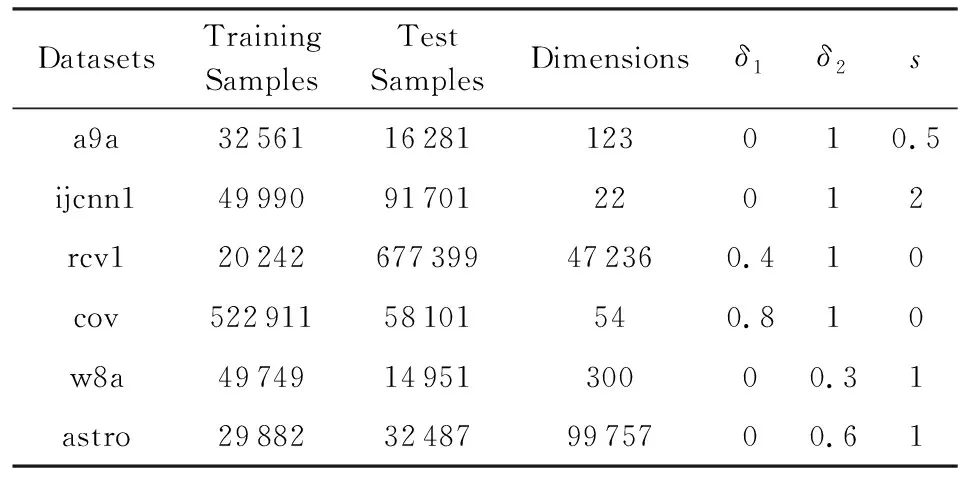
Table 1 Description of Standard Datasets表1 標準數(shù)據(jù)庫描述

為了進行公平地比較,所有的實驗都在隨機示例序列上重復(fù)計算了10次,取平均值作為最后結(jié)果,最大迭代次數(shù)均設(shè)定為10 000次.在實驗中固定β=0.9,取δ1=0,δ2=1,s=0,s=1分別表示TPUM框架下的SHB與SNAG;δ1=1,δ2=0.5,s=0時為QHM.6個數(shù)據(jù)庫中的TPUM參數(shù)選取如表1所示,分別標記為TPUM1至TPUM6,可以粗略地幫助我們看出3個參數(shù)的敏感性.

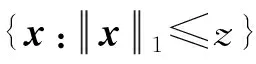
3.3 實驗結(jié)論

圖1為時變步長與固定步長對于收斂性影響的比較圖,其中帶有time-varying的曲線表示使用的是時變步長.實驗驗證,盡管固定步長在計算上為常數(shù)更為簡單,但時變步長可以達到和固定步長幾乎一致的最優(yōu)收斂速率.而在實際的機器學(xué)習(xí)問題中,如果數(shù)據(jù)集樣本發(fā)生變化,或者處理大規(guī)模數(shù)據(jù)時,使用時變步長的方法無疑更具有實用性.

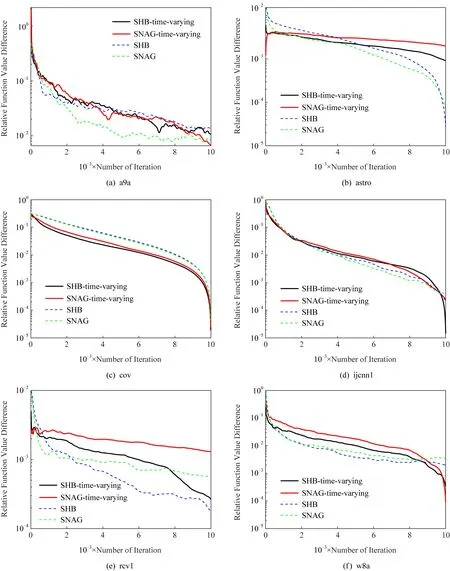
Fig. 1 Comparison of convergence rates with time-varying and constant step sizes圖1 時變步長與固定步長收斂速率比較圖

圖2為所提TPUM收斂性比較圖.如圖所示,在有約束情況下,從添加不同超參數(shù)的TPUM曲線可以看出，整體的收斂趨勢沒有改變.與現(xiàn)有的DA方法相比,TPUM方法的幾種變體,即SHB，SNAG和QHM與TPUM均有一致的收斂趨勢,在迭代8 000步后，5種算法基本都能達到10-2的精度,這與本文的理論分析結(jié)果是吻合的,說明了TPUM具有最優(yōu)平均收斂速率.

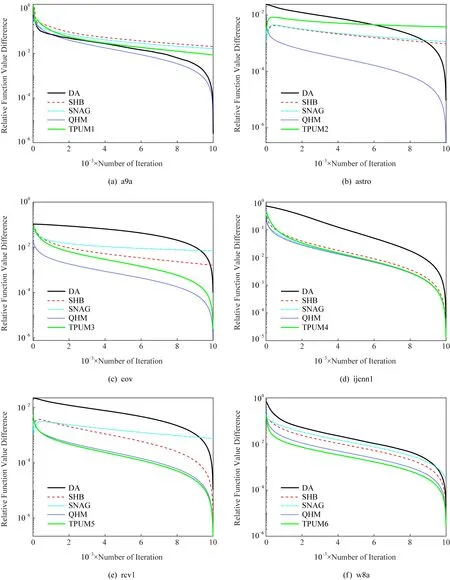
Fig. 2 Comparison of convergence rates圖2 收斂速率比較圖

4 結(jié) 論

本文提出了一種更一般的統(tǒng)一化動量方法TPUM,包括了目前典型的統(tǒng)一框架SUM和QHM.其次,證明了所提出的TPUM方法在約束情況下具有最優(yōu)的平均收斂速率,從而保證了添加動量不會影響標準梯度下降法的收斂性能以及動量方法對機器學(xué)習(xí)問題的可應(yīng)用性.

眾所周知,相比于平均輸出,個體輸出具有更好的稀疏性,但個體收斂性較難獲得.目前對于HB，NAG的個體收斂性已經(jīng)有所突破[1-3].能否得到TPUM的個體收斂性結(jié)論顯然值得考慮.另一方面,2015年Kingma等人提出一種Adam(adaptive moment estimation)方法,實際上是在HB基礎(chǔ)上對步長的設(shè)置加以改進,以得到更好的收斂性能,目前在深度學(xué)習(xí)中被廣泛使用[24],而QHM與Adam的結(jié)合也已經(jīng)有所研究[6].將本文提出的TPUM與Adam結(jié)合,進一步提升動量方法在深度學(xué)習(xí)中的性能將是我們下一步的研究方向.