基于FP腔的大量程超聲解調系統研究

高在青,張示城,鈕月萍,龔尚慶

(華東理工大學 理學院,上海 200237)

0 引 言

超聲波傳感器在非破壞結構健康檢測、醫學檢測以及三維測量等方面具有重要應用意義[1]。近年來,基于光纖布拉格光柵(Fiber Bragg Grating,FBG)的超聲波傳感器因其具有體積小、靈敏度高、抗電磁干擾能力強和擴展性強等優勢越來越受到廣泛的關注[2-3]。

超聲波檢測的原理是測量超聲波引起的FBG光譜移動,需要具有亞微應變的分辨率和高于千赫茲的帶寬,其關鍵技術在于實現FBG光譜信號的高精度解調。文獻[4-5]利用寬帶光源和匹配FBG進行解調,但其系統噪聲較大；文獻[6-7]報道了可利用窄帶光源減小系統噪聲,但成本較高且無法多路復用,缺乏實用價值；光譜信號解調的靈敏度取決于光譜線寬,文獻[8-9]利用π相移FBG(π-phase shifted-FBG,π-FBG)有效提高了探測靈敏度,然而π-FBG的窄線寬導致解調系統量程很小；為了提高量程,文獻[10]提出了利用雙法布里珀羅(Fabry Perot,FP)濾波器解調方案,但該方案中僅將量程提高了約兩倍,且系統復雜、成本高,無法擴展。上述方案主要都是基于窄帶邊緣濾波法[1],普遍存在測量靈敏度和量程相互制約的問題。

為了解決上述問題,本文在文獻[10]的基礎上提出了一種基于FP腔和π-FBG的大量程解調方案。本文在理論上詳細分析了利用FP腔的多個縱模和可調諧濾波器進行解調的原理,該方案具有高靈敏度,同時可以利用多個縱模構建解調器陣列有效地提高量程。本文還通過耦合模理論進行了數值仿真分析,仿真結果表明,本方案還具有很好的線性度且響應帶寬可達到數百k Hz。

1 理論模型

圖1所示為本文所提解調系統的原理圖,寬帶光源出射的光經循環器進入π-FBG被反射,反射光經循環器進入由FP腔、可調諧濾波器、光電探測器和控制器組成的解調部分。π-FBG的布拉格波長為

式中:neff為光纖纖芯的有效折射率；Λ為光柵周期。超聲沖擊會引起π-FBG的布拉格波長移動,且移動量與超聲的聲壓ΔP(t)成正比[11],比例系數由光纖的材料決定。因此,通過檢測π-FBG光譜的移動就可以測量超聲信號。

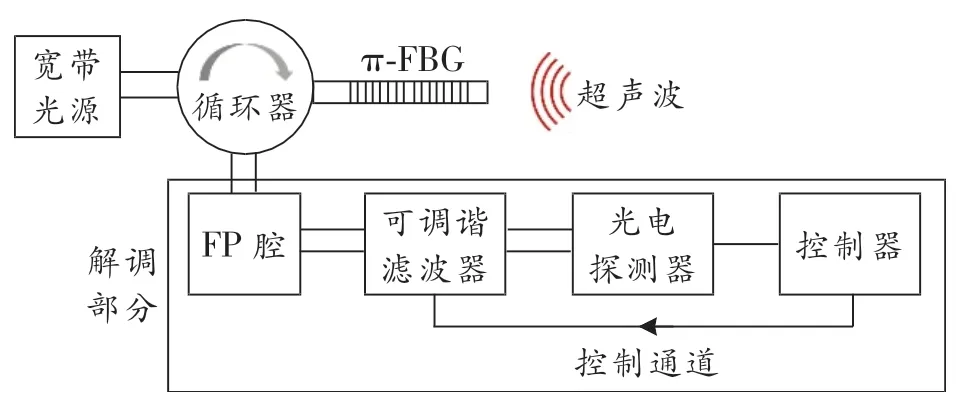
圖1 解調系統原理圖

圖2所示為典型的π-FBG反射譜,圖中b為窄峰帶寬。通常可以利用窄帶邊緣濾波法進行解調,光譜的移動量為[1]

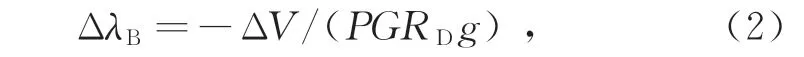
式中:ΔV為移動前后光電探測器輸出電壓的變化；P為輸入光通過窄帶濾波器后的功率；G為光柵的斜率(通常可近似為常數)；RD和g分別為光電探測器的響應因子和增益系數。邊緣濾波法的解調靈敏度取決于G的大小,解調范圍取決于b。對于窄帶邊緣濾波法,系統靈敏度越高就會導致量程越小,兩者是相互制約的[8]。

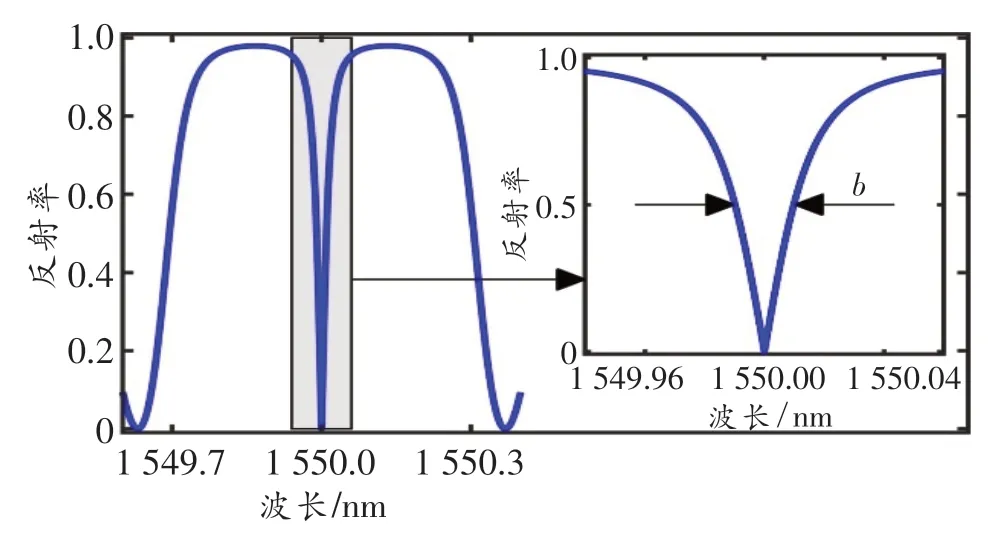
圖2 π-FBG反射譜

本文提出了利用FP腔的多個縱模構建濾波解調器陣列擴大量程的方案。FP腔的縱模可看成是一個頻率梳[λ1,λ2,…,λi,…,λN],其中λi為第i個縱模,N為用于解調的縱模數量。利用可調諧濾波器可使每一個縱模單獨作為一個濾波解調器。可調諧濾波器由壓電陶瓷(Piezoelectric Transducer,PZT)驅動,其帶寬和FP腔的自由光譜區大小λFSR相當。通過調節PZT的電壓,當可調諧濾波器中心波長與FP腔的某一個縱模波長相等時,就可測量出反射光通過該縱模后對應的光電探測器電壓。在初始時刻 可 以 標 定 每 一 個 縱 模[λ1,λ2,…,λi,…,λN]對應的PZT驅動電壓為[u1,u2,…,ui,…,uN],其中ui為第i個縱模對應的PZT驅動電壓。測量時,通過快速掃描PZT的驅動電壓就可得到每一個縱模對應的光電探測器輸出電壓[V1,V2,…,Vi,…,VN],其中Vi為第i個縱模對應的光電探測器輸出電壓。連續地周期性掃描就可以實時監測每一個縱模對應的光電探測器的輸出電壓變化。需要注意的是,這里每一個縱模對應一個可測量的波長區域。通過選擇合適的FP腔參數,可使其λFSR與π-FBG反射譜帶寬b相當。則不論π-FBG布拉格波長是多少,始終存在兩個縱模分別位于窄峰的兩側可以同時用于解調,圖3所示為π-FBG受超聲波沖擊移動前后的光譜圖。因此,對于不同的布拉格波長,可以選擇對應的兩個縱模進行解調。本方案的量程主要受限于可調諧濾波器的波長調諧范圍(通常可達數nm)。相比于文獻[10]中的量程(約為0.2 nm),本方案中量程得到了極大地提高。

圖3 π-FBG受超聲沖擊移動前后的光譜

下面我們詳細分析如何根據光電探測器的輸出電壓來解調光譜移動量。假設初始時刻t0,模式λi和λi+1都處于π-FBG窄峰的半高峰位置,對應的光電探測器電壓為=V0。在t0+Δt時刻,π-FBG反射譜移動了ΔλB,則此刻處于窄峰附近的縱模變為λj和λj+1,對應的光電探測器電壓和表示為

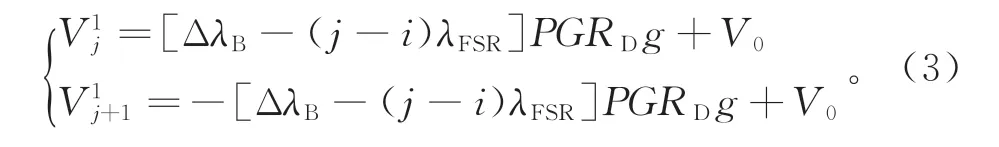
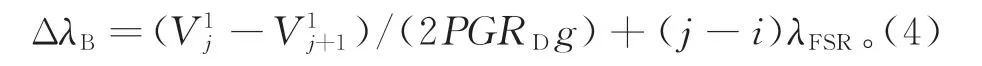
由上述分析可知,本方案可利用π-FBG窄峰附近的兩個縱模作為一組解調器同時解調,這樣不僅可以擴大量程,還可以將測量靈敏度提高兩倍,并可以避免窄帶邊緣濾波法中存在的雙值問題[2]。本方案的采樣頻率取決于PZT的響應頻率fPZT和用于解調的縱模數量N,可表示為fPZT/N。通常fPZT可達M Hz量級,而N取決于待測信號的振幅。

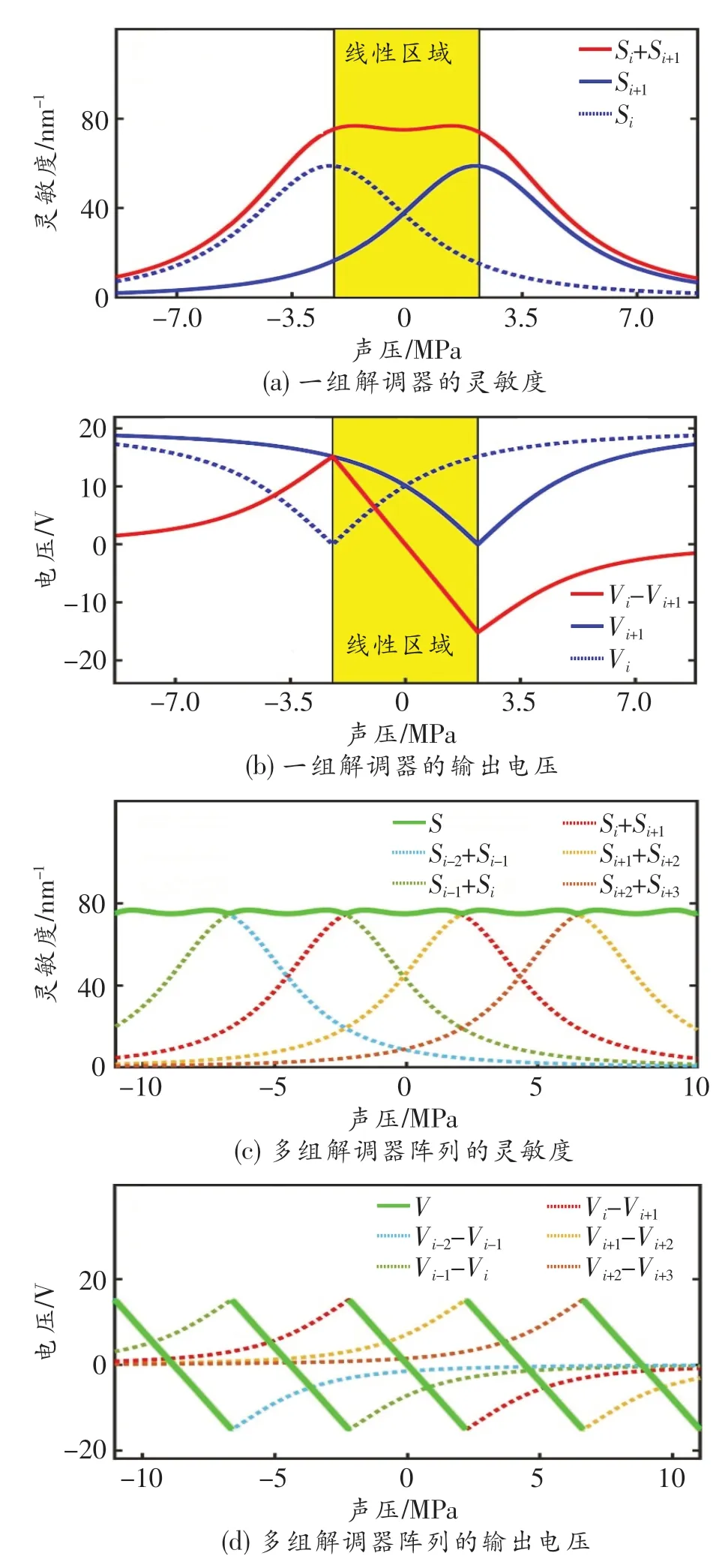
圖4 系統靈敏度和輸出電壓隨超聲波聲壓的變化

2 數值仿真與分析

數值仿真中π-FBG的光譜變化可通過耦合模理論計算[12]。取π-FBG的光柵長度為5 mm,有效折射率為1.445 3,折射率調制深度為3×10-4,布拉格波長為1 550 nm,光纖材料的其他參數參照文獻[11]。則根據所取參數可得π-FBG的帶寬約為0.02 nm,半高峰位置的斜率約為39 nm-1。取FP腔長度約為6 cm,反射率為95%,則可得到縱模線寬約為0.32 pm,自由光譜區約為0.02 nm,因此對應的可調諧濾波器帶寬可取為0.02 nm。對于光源和光電探測器,取光功率為3 d Bm,光電探測器響應因子為1 V/m W,增益系數為10,最小可分辨電壓為0.03 V/Hz1/2。

我們首先對系統靈敏度和輸出電壓隨超聲波聲壓的變化進行了數值仿真,如圖4所示。將縱模λi的靈敏度定義為(i=1,2,…,N),式中:r為反射率；λ為光波長。首先考慮一組解調器的情況,以λi和λi+1為例,如圖4(a)所示。由圖可知,單個縱模的靈敏度隨聲壓的變化起伏較大,而兩個縱模的總靈敏度Si+Si+1在較大區域內幾乎保持不變,可以將該區域稱為線性區域。因此對應的輸出電壓與聲壓呈現很好的線性關系,即系統具有很好的線性度,如圖4(b)所示。然而一組解調器的線性區域仍然較小,當考慮多組解調器構成的陣列時,系統靈敏度S就可在整個量程范圍內都幾乎保持不變,如圖4(c)所示。而由圖4(d)可知,輸出電壓V則隨著聲壓呈現周期性的線性變化。這是因為FP腔的縱模是等間距分布的,這也與式(3)和(4)相吻合。因此數值模擬結果進一步驗證了理論模型的正確性,此外該方案還可以很好地解決窄帶邊緣濾波法測量線性度不好的問題。

下面討論解調系統對于不同振幅和頻率超聲波信號的解調能力。假設PZT的響應頻率為2 MHz,超聲信號是一個包含10個周期的脈沖信號,如圖5中紅色實線所示,數值仿真采集的超聲信號如圖5中藍色虛線所示。圖5(a)從上到下分別對應聲壓為2、10和22 MPa的超聲信號,其頻率fs均為100 k Hz。由圖可知,隨著超聲波聲壓振幅增大,每個周期內的采樣點會減少,進而導致采樣圖形的失真。這是因為超聲振幅的增大會導致用于解調的縱模數量增加,進而導致采樣頻率的減小。圖5(b)所示為當fs分別為100、300和600 k Hz時聲壓為2 MPa的超聲信號的采樣結果。由圖可知,對于振幅一定的超聲信號,隨著其頻率的提高,同樣的采樣頻率條件下,每個周期內的采樣點也會減少,進而導致采樣圖形的失真。因此,最終采樣圖形的保真度取決于超聲信號的頻率和用于采樣的縱模數量。根據數值仿真計算可知,當fsN≤fPZT/2時,采集的圖形具有很好的保真度。此外,根據光電探測器的最小可分辨電壓可以計算得到該方案的最小可分辨壓強為4.4 kPa/Hz1/2,對應的最小可分辨應變為62 nε/Hz1/2,并且測量帶寬可達百k Hz。文獻[10]中使用的是切趾FBG,其靈敏度較低(με/Hz1/2量級),而本方案使用的π-FBG在靈敏度上也有一定提升。

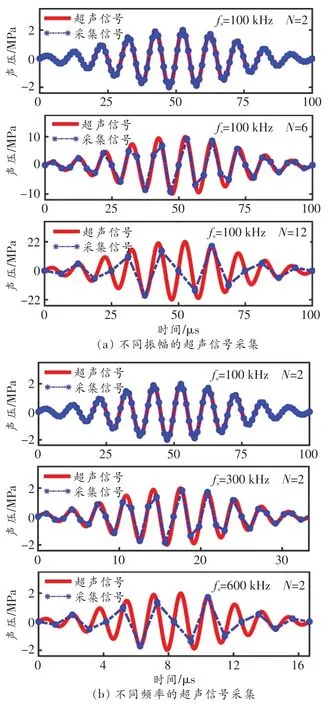
圖5 不同振幅和頻率的超聲信號采集

3 結束語

本文提出了一種基于FP腔和π-FBG的大量程解調方案。本方案利用FP腔的兩個縱模作為一組解調器可以將探測靈敏度提高兩倍,并且具有很好的線性度。擴展到多個縱模構建的解調器陣列,可以極大地提高量程,理論上量程可達數nm。數值仿真結果表明,該方案還具有較高的測量靈敏度,最小可分辨應變為62 nε/Hz1/2,并且具有數百k Hz的測量帶寬。本方案可以有效地解決超聲測量中測量靈敏度和量程相互制約的問題。