一種新的繞組變形測試儀校準數據處理方法

吳 華,米思蓓,李 剛,陳習文,郭子娟,余宏明

(1.國網重慶市電力公司電力科學研究院，重慶 404100；2.中國電力科學研究院有限公司，湖北 武漢 430070；3.中國地質大學(武漢)工程學院,湖北 武漢 430074)

電力變壓器是電力系統的重要設備之一，對電力運行安全起著至關重要的作用。變壓器繞組發生局部變形后，必然會引起其內部參數的變化，通過對這些參數的測量和分析，就可以判斷繞組是否存在變形，但傳統方法通常難以對其內部參數進行全面檢驗。對于繞組變形測試儀的掃描頻率精確度、檢測精確度、選頻濾波特性、阻抗匹配方式等關鍵技術指標，必須借助專用的衰減器來實現校準檢測。但采用該衰減器對繞組變形測試儀進行實際檢測中受很多不確定性因素的影響，其校準結果存在不確定度。針對校準結果存在的不確定度，實際操作中需要通過多次試驗來減弱這種誤差帶來的影響。但在現有的試驗條件下，通過多次試驗需要花費大量的時間和精力[1]。本文基于二維非均勻插值算法甄別出校準結果中的不合理數據，并通過多次試驗驗證數據挑選的準確性和插值結果的合理性。

克里金插值是一種基于統計學變差模型的空間插值方法。該方法利用區域變量的原始數據和變異函數的結構特征估計未知點的屬性值，是一種最優、線性、無偏估計方法。對于具有空間和時間相關性的插值數據，時空克里金插值算法可以用來較好地考慮時空數據的時空特征，從而獲得更準確的插值結果。目前時空克里金插值算法已廣泛運用于地質、氣象、礦產資源、工程應用等多個領域[2]。如Pucci等[3]、Rouhani等[4]、Jaquet[5]、Bardossy等[6]、Nobre等[7]、Tarboton等[8]、Piotrowski等[9]研究了時空克里金算法在水文地質方面的應用；Bogaert[10]、H?st[11]、Lin等[12]將時空克里金算法應用于模擬數據；Kerwin等[13]將時空克里金算法應用于醫學圖像中估計心臟運動；Jost等[14]將物理確定性蒸發模型與時空地質統計插值相結合，用來預測土壤儲水量；魏玉珍等[15]運用時空克里金插值算法對水庫富營養化空間格局進行分析，并提出了防治對策；Gething等[16]將局部時空克里金算法應用于國家門診瘧疾數據集的插值；Liang等[17]將時空克里金插值算法應用于空氣污染數據的非平穩時空結構中。時空克里金插值算法在普通克里金插值算法的基礎上考慮了數據的時間特性，得到了更好的插值效果。

本文提出一種適用于變壓器繞組變形測試儀校準裝置校準數據的二維非均勻克里金插值算法。該方法首先基于校準數據的試驗點在不同頻率上的非均勻性，對每個頻率上設置一個頻率權重[ai]，其中i代表不同頻率的試驗點，并針對校準數據的試驗點在不同衰減量上的非均勻性，對不同衰減量設置一個衰減量權重[bj]，其中j代表不同衰減量的試驗點;然后針對繞組變形測試儀在不同頻率下測得的衰減量顯示值與標準值之間的差值作為插值對象構建二維變差函數模型，即每一個測試儀的校準數據，構建一個變差函數模型；最后通過優化算法尋得的權重值組合{[ai],[bj]}用來建立二維非均勻克里金差值算法，重構繞組變形校準數據的頻率與衰減量的非均勻關系，以減弱校準裝置校準誤差對二維變差函數模型的影響。

1 基本算法

1.1 克里金插值算法

克里金插值的主要作用是估算空間未采樣點的屬性值[18]。假設存在某一研究區域D，區域化研究變量Y(x)為區域內X處的測量值，若區域內存在某一未采樣點x，其估計值為Y*(x)，則Y*(x)可以通過一個線性關系來估算：

(1)

式中:Y*(x)為x處的估計值；n為實際測量數量；Y(xi)為第i個位置處(xi)的實際測量值；αi為第i個位置處實際測量值的位置權重。

αi是一套使插值誤差最小的最優系數，其需要滿足如下無偏估計和估計方差最小兩個條件：

(2)

根據拉格朗日乘數法對公式(2)進行簡化，可得到：

(3)

式中:c(xi,xj)為Y(xi)和Y(xj)的協方差函數;c(x0,xj)為待插值點與已知樣點之間的協方差；μ為拉格朗日乘子。

克里金插值算法的變差函數計算公式如下：

[i=1,2,…,n(h)]

(4)

式中:γ(h)為滯后距離h時對應的變差函數值；xi為第i個采樣點;h為滯后距離;n(h)為滯后距離h時的樣本點總數。

根據變差函數γ(h)與協方差函數之間的關系，通過變換上述方程組，可得到克里金方程矩陣如下：

(5)

通過克里金插值算法求取未采樣點屬性值時，需要先對已知采樣點數據進行分析，求取試驗變差函數值，再通過理論變差函數模型擬合離散的試驗變差函數值，獲得采樣點數據的變差函數模型。即先根據公式(5)求取克里金插值中的權值，再將求解出的權值帶入公式(1)中，求取未采樣點的屬性值。

1.2 粒子群算法

粒子群算法(Particle Swarm Optimization,PSO)是一種通過信息共享，尋求到最優解的優化算法。該算法適用于非線性、非結構化解的尋優[19-21]。粒子的質量是用適應度函數來衡量的，它反映了解的最優性。所有潛在解的集合被稱為解空間，一個潛在解被稱為一個位置，記為Pos。沒有質量、沒有大小的粒子在解空間中以速度v運動，最優解是通過不斷更新粒子的位置和速度得到的，而粒子在更新過程中朝個體最優位置Pib和群體最優位置Pgb移動。通過下式更新粒子的速度和位置：

vi+1=ω×vi+c1×Rand×(Pib-Posi)+c2×Rand×(Pgb-Posi)

(6)

Posi+1=Posi+vi+1

上式中:下標i表示PSO算法的迭代次數；Posi表示在第i次迭代中粒子當前的位置；vi表示在第i次迭代中粒子的速度；vi+1和Posi+1分別代表粒子更新后的速度和位置;Rand是一個(0,1)范圍內的隨機數；Pib表示粒子的個體最優位置；Pgb表示粒子的群體最優位置。

本文利用PSO算法首先將二維非均勻克里金插值中的衰減量權重和頻率權重組合{[ai],[bj]}的維度作為解的維度；然后將插值結果的均方誤差作為適應度函數；最后找到最優的權重組合能使得插值結果最好。

2 研究方法

本文提出的二維非均勻克里金插值方法給不同衰減量和不同頻率賦予不同的權重值，并利用PSO算法對標準二維克里金算法進行重構，尋求適合于繞組變形測試儀校準裝置校準數據特性的二維非均勻克里金插值算法,在不需要進行多次重復試驗的情況下，減少了測量不確定度對試驗結果的干擾。

2.1 二維克里金插值算法

二維克里金插值算法是一種基于樣本空間統計相關的最優、線性和無偏估計量的內插方法。在常見的時空克里金插值中，考慮了空間和時間的相關性[22]。假設Z(s,t)是時空區域化變量，(s,t)表示時空域中的樣本點位置。從空間域延展到時空域后的克里金模型如下：

(7)

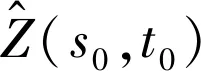
(8)

二維克里金插值算法的變差函數方程如下：

(9)

式中:γ(rs,rt)為變差函數值；hs和ht為對應的樣本之間在s和t兩個不同維度的距離；Z(si,ti)為點i處的觀測值；Z(si+hs,ti+ht)為與Z(si,ti)在第一維度上相距hs、第二維度上相距ht的點的觀測值；n(hs,ht)是二維空間距離為hs和ht的樣本點對的總數。

二維克里金插值中通過下式求解最小誤差和無偏估計條件:

(10)

式中：γst表示二維可分離型變差函數。

二維克里金插值算法通過二維空間域的變差函數將不同的空間數據結合起來，通過增加普通克里金插值的維度提高了二維數據的插值效果。在實際應用中，不同維度的空間中變量的量綱不同，二維距離不能簡單地運用各自維度的距離疊加來表示。而簡單的二維克里金插值算法無法反映繞組變形測試儀校準裝置校準數據的特性，因此本文提出了利用PSO算法構建二維非均勻克里金插值算法來解決此問題。

2.2 二維非均勻克里金插值算法

Z(x,f)是一個定義在非均勻二維空間域中的區域化變量，其中x表示樣本點的衰減量位置坐標，f表示頻率域中的位置點。如果采樣點的數量為n，則二維非均勻域中的克里金模型定義如下：

(11)

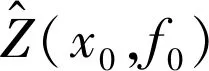
在非均勻二維域中，變差函數值的大小與兩點之間的二維空間距離密切相關，定義非均勻二維變差函數的計算公式為

(12)

式中：pf表示非均勻二維空間域中的一個樣本點；h表示兩個樣本點之間的距離；γpf(h)為變差函數值。

非均勻二維變形場模型給出的最優距離求解方法可以有效地用于測量非均勻二維空間域中的兩個樣本點之間的距離h。最優距離方案表示如下：

(13)

式中：[ai]和[bj]為POS算法尋求的最優權重系數；Sij為樣本點的二維數據(其中，i表示選取的頻率點，本文中i=1,2,3,4；j表示不同衰減量，j=1,2,3,…,9)。

在求得兩個樣本點之間的距離h和變差函數值γpf后，使用h和γpf進行理論變差函數模型的擬合。根據理論變差函數模型和待插值點與已知點之間的二維空間距離，即可求得對應的變差函數值，并將其用于克里金方程組的求解。在非均勻二維空間域中其求解的公式如下:

(14)

二維非均勻克里金插值的一組權重系數λi可以通過求解方程得到，該組權重系數是一套使插值誤差最小的最優系數，其維度與研究區域中已知點的個數相同。將λi代入二維非均勻域中的克里金模型定義中，即可得到待插值點的屬性值。

3 案例分析

3.1 模型構建

本文選取型號為RZB-1的變壓器繞組變形測試儀校準裝置，在溫濕度適宜的情況下，使用二維非均勻克里金插值算法針對多個繞組變形測試儀校準裝置的基本校準數據的誤差數據進行插值。原始的校準數據是在測試儀器設備4個頻率段(1 kHz、10 kHz、100 kHz、300 kHz)和9個衰減量(-1.21 dB、-2.02 dB、-4.30 dB、-6.12 dB、-9.90 dB、-20.03 dB、-29.82 dB、-40.30 dB、-49.85 dB)進行采集的，本文選取該校準裝置對7臺設備的校準數據值作為訓練樣本，構建二維非均勻克里金插值模型，選取4臺設備的校準數據值作為測試樣本，檢驗該模型的有效性。衰減量的數值與校準誤差不在一個數量級上，如果將原始的校準數據作為插值對象，難以反映校準誤差。因此，本文選用衰減量顯示值(dB)與標準值(dB)之間的差值作為插值對象，將差值構成的二維數據Sij作為非均勻二維域中的區域化變量。綜合考慮研究對象的二維特性，將曲線的幅值數據構建為二維變形場模型，如下式：

mod=(aibjSij) (i=1,2,3,4;j=1,2,…,9)

(15)

其中，下標i表示不同的頻率；下標j表示不同的衰減量。

選擇7個校準樣本數據作為試驗數據，運用POS算法對校準數據進行參數尋優，將二維非均勻克里金插值交叉驗證結果的均方誤差作為適應度函數。POS算法按照經驗設置初始參數學習因子c1、c2均為1.5，慣性權重w為0.729 8，初始化種群大小為20。

首先在0.95～1.05的范圍內初始化種群個體位置，粒子的維度為13，將解空間的范圍設置在[0.50,2.00]，解的精度設置為0.01，如下式：

particle1=[a1,a2,a3,a4,b1,b2,b3,b4,b5,b6,b7,b8,b9]

(16)

當適應度函數收斂或者迭代次數超出規定次數后終止。然后通過POS算法得到二維非均勻克里金插值模型的13維權重最優解為[1.10,1.07,1.06,0.94,0.90,0.67,0.52,0.85,0.95,0.95,0.90,0.94,0.90]。

最后使用上述13維權重構建插值數據，并完成二維變差函數的調整，如下式:

(17)

其中，每一列為同一衰減量不同頻率點、每一行為同一頻率不同衰減量的二維非均勻克里金插值調整后的數據。

為了驗證該處理方法的有效性，本文針對數據點a3b9S39重復做了10次試驗，其試驗結果見圖1。在圖1中，對這7個校準數據的10個試驗數值的最大值、最小值、平均值進行了對比研究，并畫出試驗中所用的數值(即試驗用值)和運用二維非均勻克里金插值計算結果的連線。

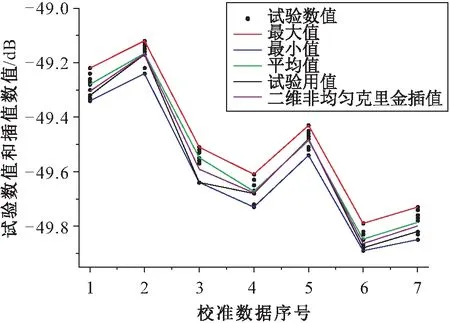
圖1 數據點a3b9S39的10次試驗結果Fig.1 10 test results of data point a3b9S39

由圖1可見，通過本文處理方法插值出來的數據更接近多次校準數據的平均值，比起試驗用值來說更少地選用靠近極值的數據。

3.2 插值結果

本文使用二維非均勻克里金插值算法對變壓器繞組變形測試儀校準裝置的基本校準數據的誤差數據進行插值。首先將{[ai],[bj]}系數值乘以對應校準數據與衰減量的差值，利用二維非均勻變差函數計算各個點的變差函數值，得到變差函數模型；然后計算待插值點和所有已知樣本點之間的距離并代入變差函數模型中得到對應的變差函數值；最后求解算法的方程組得到一組權重系數，將權重系數和已知樣本點的差值進行加權調整后，運用二維非均勻克里金插值方法對所有數據進行遍歷插值，即可得到數據的修正值，再將該數據加上衰減量，就成為調整后的最終數據了。數據點S394次校準數據與衰減量差值的插值結果見圖2,數據點S394次校準數據的多次試驗結果與二維非均勻克里金插值結果對比見圖3。

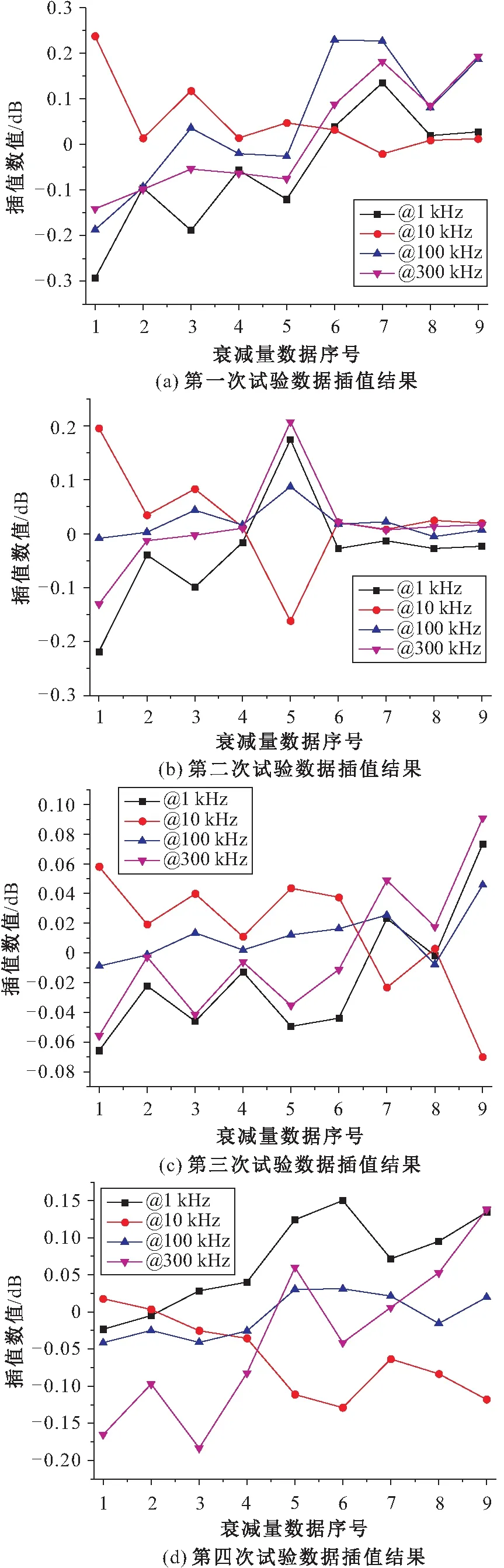
圖2 數據點S394次校準數據與衰減量差值的插值 結果Fig.2 Interpolation results of the difference between four different calibration data and attenuation magnitude of the data point S39

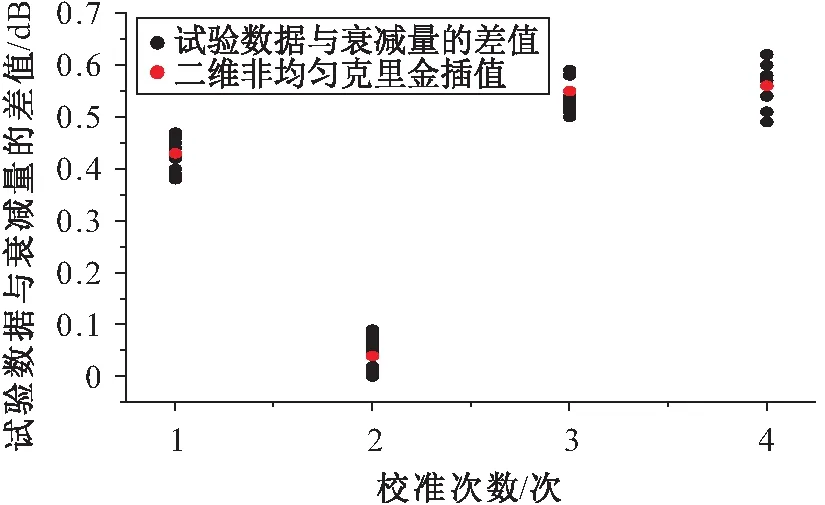
圖3 數據點S394次校準數據的多次試驗結果與二維 非均勻克里金插值結果對比圖Fig.3 Comparison diagram of four calibration data of data point S39 between multiple tests and two- dimensional non-uniform Kriging interpolation

由圖2和圖3對比可知，對數據點S39在第一臺測試設備上，多次重復試驗的試驗數據與衰減量的差值在0.38 dB～0.47 dB之間，由校準結果分散性引入的不確定度分量為0.04 dB，而經過二維非均勻克里金插值后的數據差值為0.43 dB，與多次校準數據的平均值僅僅相差0.01 dB,大大地弱化了因為校準結果分散性而造成的不確定度；后面3臺設備的結果也同樣證明了該方法的有效性。因此，二維非均勻克里金插值方法應用于變壓器繞組變形測試儀校準裝置校準數據的處理中，能有效地降低因為校準結果分散性而造成的不確定度，提高校準的精度。

4 結 論

本文提出了一種基于二維非均勻插值算法的變壓器繞組變形測試儀校準數據處理方法。對同一種計量標準，通過對不同的多臺測試儀器的校準結果進行了二維非均勻插值處理，利用該方法提取了與計量標準相關的特征，并運用該特征對后面校準結果進行了調整與校準。試驗證明：該方法有效地降低了校準結果分散性而引入的不確定度，與直接校準相比，無需花費大量時間進行多次試驗來減少誤差，提高了繞組變形測試儀校準數據質量和校準精度，對測試儀的校準評價更為準確，保障了電網的安全運行，具有很好的社會效益和經濟效益。