利用多孔抽水試驗(yàn)確定承壓-無(wú)壓流條件下承壓含水層的水文地質(zhì)參數(shù)

李 丞，王寧濤，胡 成，常 威1，，孫 偉1，，黃 琨

(1.中國(guó)地質(zhì)大學(xué)(武漢)研究生院，湖北 武漢 430074；2.中國(guó)地質(zhì)大學(xué)(武漢)環(huán)境學(xué)院，湖北 武漢 430074；3.中國(guó)地質(zhì)調(diào)查局武漢地質(zhì)調(diào)查中心(中南地質(zhì)科技創(chuàng)新中心)，湖北 武漢 430205)

確定含水層的滲透系數(shù)K、給水度μ等水文地質(zhì)參數(shù)是開(kāi)展地下水資源量評(píng)價(jià)的基礎(chǔ)[1-2]。抽水試驗(yàn)是確定松散巖類孔隙含水層水文地質(zhì)參數(shù)最常用的技術(shù)方法[3-5]。根據(jù)抽水試驗(yàn)獲取的含水層水位隨時(shí)間的變化曲線，并結(jié)合水文地質(zhì)條件選擇相應(yīng)的井流模型即可求取含水層的水文地質(zhì)參數(shù)。對(duì)于承壓含水層，常用的求參方法有基于泰斯(Theis)承壓井流模型的Jacob直線圖解法、標(biāo)準(zhǔn)曲線配線法[6-7]。對(duì)于潛水含水層，常用的井流模型包括泰斯?jié)撍髂Ｐ汀⒖紤]含水層滯后給水的博爾頓(Boulton)模型以及考慮彈性釋水的紐曼(Neuman)模型[8-10]。在承壓含水層中，當(dāng)抽水井持續(xù)抽水引起地下水水位降至隔水頂板以下時(shí)，抽水井中地下水由承壓狀態(tài)往無(wú)壓狀態(tài)轉(zhuǎn)化，出現(xiàn)承壓-無(wú)壓流并存的現(xiàn)象。而針對(duì)承壓含水層中承壓-無(wú)壓狀態(tài)并存條件下的井流模型有Moench承壓-無(wú)壓井流模型和Chen承壓-無(wú)壓井流模型[11-13]。

1 研究區(qū)概況

研究區(qū)位于江漢平原北部肖家港地區(qū)，該地區(qū)地勢(shì)平坦，整體表現(xiàn)為北高南低、東西高中間低，澴河兩側(cè)往河床微微傾斜。研究區(qū)內(nèi)地表大部分面積為第四系所覆蓋，區(qū)內(nèi)僅在北部、東北部地勢(shì)相對(duì)較高處出露少量青白口系武當(dāng)群(Qbw)變質(zhì)巖、震旦系(Z)硅質(zhì)巖以及古近系(Ey)砂巖、砂礫巖，見(jiàn)圖1。

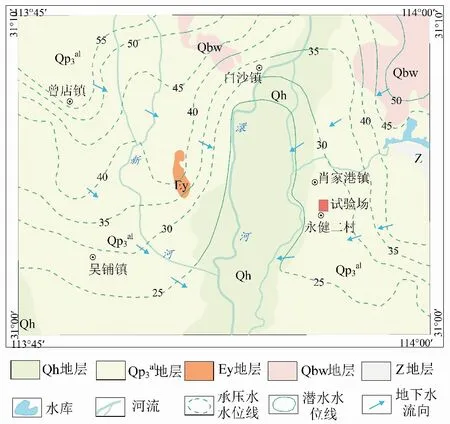
圖1 研究區(qū)水文地質(zhì)圖Fig.1 Hydrogeological map of the study area

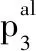
圖2 研究區(qū)地下水補(bǔ)徑排特征示意圖Fig.2 Schematic diagram of groundwater recharge and discharge in the study area

2 多孔抽水試驗(yàn)

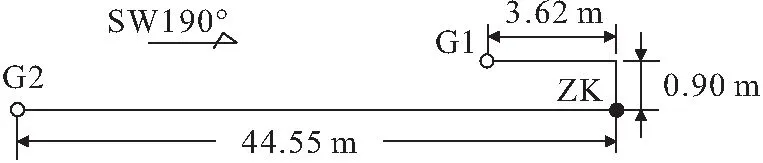
圖3 研究區(qū)水文地質(zhì)鉆孔平面位置分布Fig.3 Plan distribution of hydrogeological boreholes in the study area

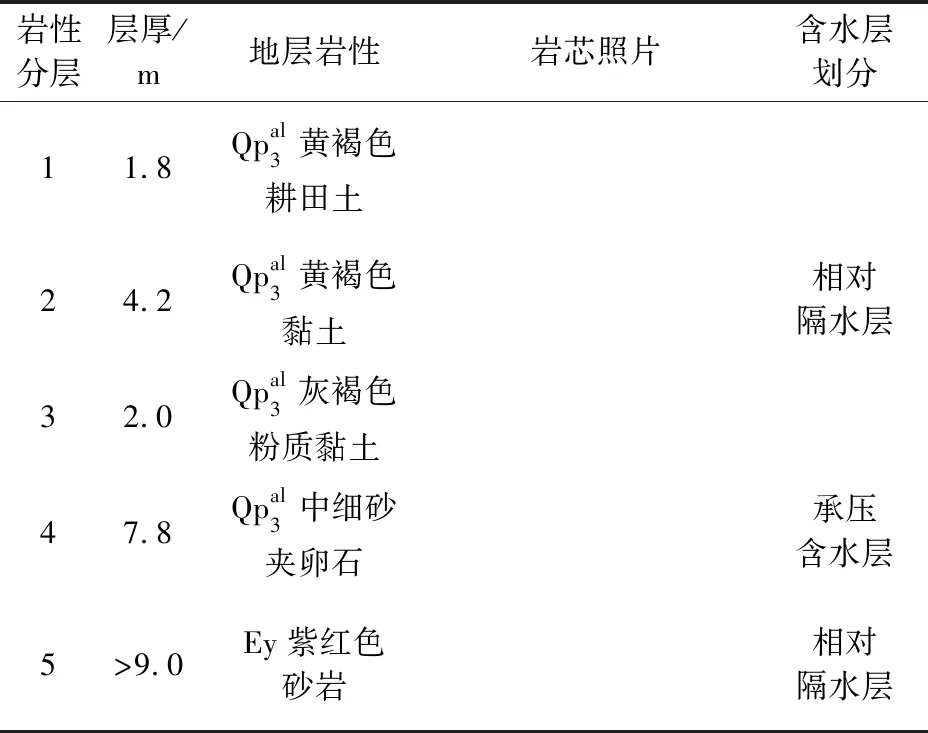
表1 研究區(qū)巖性及含水層劃分Table 1 Lithology and aquifer division of the hydrogeo-logical boreholes in the study area

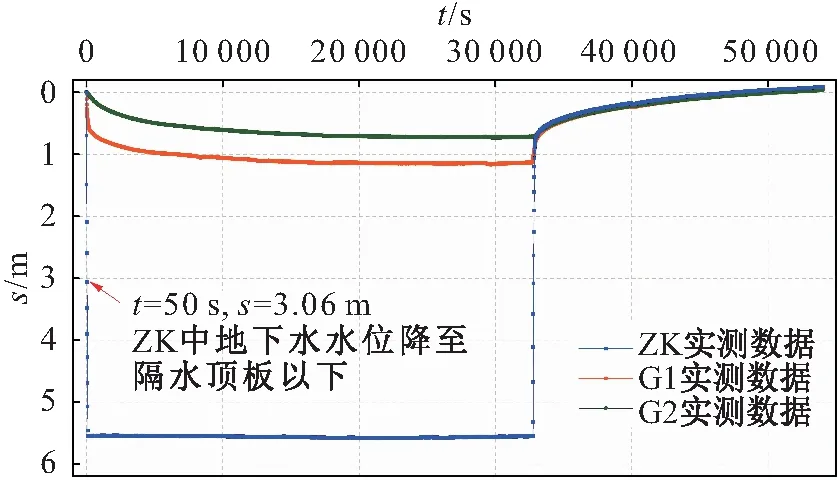
圖4 抽水井ZK和觀測(cè)井G1、G2中地下水水位降 深(s)-時(shí)間(t)曲線Fig.4 Drawdown-time curves of pumping well ZK and observation wells G1 and G2

由圖4可見(jiàn)，抽水井ZK和觀測(cè)井G1、G2中地下水水位的最大降深分別為5.57 m、1.14 m、0.72 m，其中抽水井ZK中地下水水位在抽水進(jìn)行50 s時(shí)已降低至隔水頂板以下而轉(zhuǎn)換為無(wú)壓狀態(tài)，而觀測(cè)井G1、G2中地下水水位在整個(gè)抽水過(guò)程中均高于隔水頂板，保持在承壓狀態(tài)，即本次多孔抽水試驗(yàn)過(guò)程中出現(xiàn)了無(wú)壓-承壓流并存的現(xiàn)象，并且試驗(yàn)過(guò)程中相較于承壓含水層整體降落漏斗的影響范圍很小，可以概化為無(wú)限含水層。

3 承壓含水層水文地質(zhì)參數(shù)的求解及分析

3.1 泰斯承壓井流模型的直線圖解法

對(duì)于本次多孔抽水試驗(yàn)，首先利用泰斯承壓井流模型的直線圖解法求解承壓含水層的水文地質(zhì)參數(shù)，并分析承壓含水層抽水井附近無(wú)壓區(qū)的出現(xiàn)對(duì)參數(shù)求解的影響。

在滿足泰斯假定條件下，承壓含水層空間上任意點(diǎn)的地下水水位降深為

(1)

式中：s為觀測(cè)井中地下水水位降深(L)；Q為抽水流量(L3/T)；W(u)為u的井函數(shù)，u=r2μe/4Tt[其中，T為含水層導(dǎo)水系數(shù)(L2/T)；μe為含水層彈性釋水系數(shù)；r為觀測(cè)井到抽水井的距離(L)；t為計(jì)算地下水水位降深的時(shí)刻(T)]。

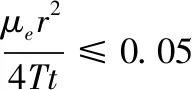
(2)

對(duì)于確定的含水層和觀測(cè)井，公式(2)中T、μe、Q、r均為常數(shù)，故s與lgt呈直線關(guān)系，此直線斜率m為

(3)

此直線與lgt軸的交點(diǎn)t0為

(4)

本文繪制了觀測(cè)井G1、G2的實(shí)測(cè)s-lgt曲線，見(jiàn)圖5。

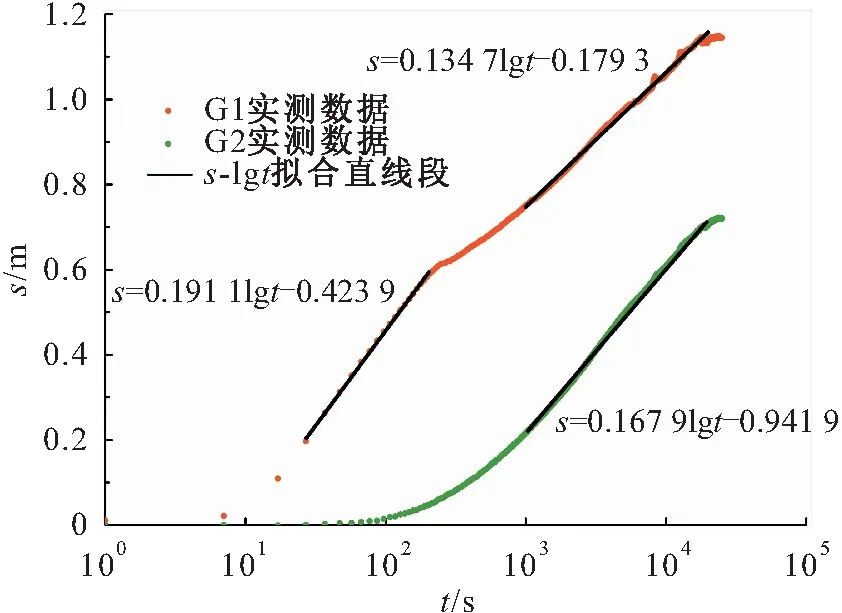
圖5 泰斯承壓井流模型的直線圖解法求解承壓 含水層水文地質(zhì)參數(shù)的示意圖Fig.5 Diagram of hydrogeological parameters estimation of the confind aquifer with Cooper-Jacob method of Theis model

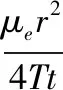
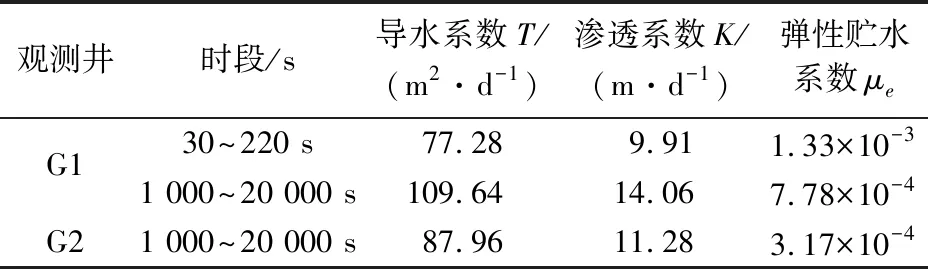
表2 泰斯承壓井流模型的直線圖解法求解承壓含水層水文地質(zhì)參數(shù)結(jié)果Table 2 Hydrogeological parameter estimation of the confind aquifer with Cooper-Jacob method of Theis model

由表2可知，利用泰斯承壓井流模型的直線圖解法處理觀測(cè)井G1、G2的地下水水位降深變化數(shù)據(jù)所求得的承壓含水層導(dǎo)水系數(shù)T值的變化幅度較小，在77.28～109.64 m2/d之間，而所求得的承壓含水層彈性釋水系數(shù)μe值的變化幅度較大，在3.17×10-4～1.33×10-3之間。其中，利用觀測(cè)井G1第二直線段與觀測(cè)井G2直線段求取的承壓含水層水文地質(zhì)參數(shù)值比較接近，而與觀測(cè)井G1第一直線段的求參結(jié)果差異較大。為了評(píng)價(jià)求參結(jié)果的準(zhǔn)確性，分別將計(jì)算得到的承壓含水層水文地質(zhì)參數(shù)代入公式(2)中反求觀測(cè)井G1、G2中地下水水位的理論降深值，并與實(shí)測(cè)降深值進(jìn)行了對(duì)比，見(jiàn)圖6。

由圖6可見(jiàn)，根據(jù)觀測(cè)井G1第一直線段所得參數(shù)計(jì)算得到的理論降深值與觀測(cè)井G1、G2的實(shí)測(cè)降深值均相差較大[圖6(a)、(d)]；根據(jù)觀測(cè)井G1第二直線段所得參數(shù)計(jì)算得到的理論降深值與觀測(cè)井G1的實(shí)測(cè)降深值較吻合[見(jiàn)圖6(b)]，但與觀測(cè)井G2的實(shí)測(cè)降深值相比則明顯偏低[見(jiàn)圖6(e)]；根據(jù)觀測(cè)井G2所得參數(shù)計(jì)算得到觀測(cè)井G2的理論降深值與其實(shí)測(cè)降深值較為一致[見(jiàn)圖6(f)]，但觀測(cè)井G1的理論降深值與其實(shí)際降深值相比則偏高[見(jiàn)圖6(c)]。根據(jù)試驗(yàn)場(chǎng)條件及抽水試驗(yàn)數(shù)據(jù)可知，含水層承壓高度為2.72 m，當(dāng)抽水持續(xù)僅50 s后抽水井的地下水水位降深已達(dá)3.06 m，利用阿勃拉莫夫公式計(jì)算此時(shí)水躍值[14]，可得此時(shí)抽水井井壁處地下水水位降深為2.98 m，即承壓含水層抽水井附近一定范圍內(nèi)地下水水力特征由承壓轉(zhuǎn)換為無(wú)壓(見(jiàn)圖7)，因此抽水初期含水層的釋水量由抽水影響范圍內(nèi)承壓含水層的彈性釋水和無(wú)壓區(qū)的重力釋水共同提供。但由于承壓含水層的重力給水度μd遠(yuǎn)大于彈性釋水系數(shù)μe，在抽水初期地下水水位降落漏斗的范圍較小，無(wú)壓區(qū)含水層的重力釋水量所占比例較大不可忽略，故此時(shí)求解的承壓含水層的給水度值是介于重力給水度與彈性釋水系數(shù)之間的綜合值；同時(shí)，由于承壓含水層的重力釋水具有滯后性，其地下水水位變化響應(yīng)速度小于純承壓含水狀態(tài)的壓力傳導(dǎo)，導(dǎo)致抽水引起的觀測(cè)井中地下水水位變動(dòng)初始響應(yīng)時(shí)間t0偏大，由公式(4)可知，這將導(dǎo)致所求承壓含水層的彈性釋水系數(shù)值偏大。隨著抽水時(shí)間的持續(xù)，地下水水位降落漏斗的整體范圍不斷擴(kuò)大，無(wú)壓區(qū)的擴(kuò)展速度逐漸變慢并趨于穩(wěn)定，承壓含水層重力釋水的影響減弱，承壓含水層的彈性釋水量逐漸占據(jù)主導(dǎo)地位，因此利用觀測(cè)井G1初期數(shù)據(jù)，即s-lgt曲線第一直線段的數(shù)據(jù)求參結(jié)果具有明顯誤差，尤其是μe的計(jì)算值明顯偏大，而利用觀測(cè)井G1中后期數(shù)據(jù)，即s-lgt曲線第二直線段的數(shù)據(jù)求參結(jié)果則比較接近實(shí)際。對(duì)于觀測(cè)井G2，由于其距離抽水井ZK的距離較遠(yuǎn)，如圖7所示，當(dāng)抽水引起的地下水水位變動(dòng)影響到觀測(cè)井G2處時(shí)，承壓含水層抽水井附近的無(wú)壓區(qū)范圍已經(jīng)基本穩(wěn)定，此時(shí)含水層無(wú)壓區(qū)重力釋水量相較于彈性釋水量幾乎可以忽略，對(duì)觀測(cè)井G2中地下水水位降深的變化幾乎沒(méi)有影響，同時(shí)對(duì)觀測(cè)井G2中地下水水位變動(dòng)初始響應(yīng)時(shí)間t0的影響也相對(duì)較小，因此利用觀測(cè)井G2的觀測(cè)數(shù)據(jù)計(jì)算承壓含水層的水文地質(zhì)參數(shù)基本滿足泰斯承壓井流模型的假定條件，其s-lgt曲線也只有一段直線段，求參結(jié)果也更符合實(shí)際水文地質(zhì)條件。

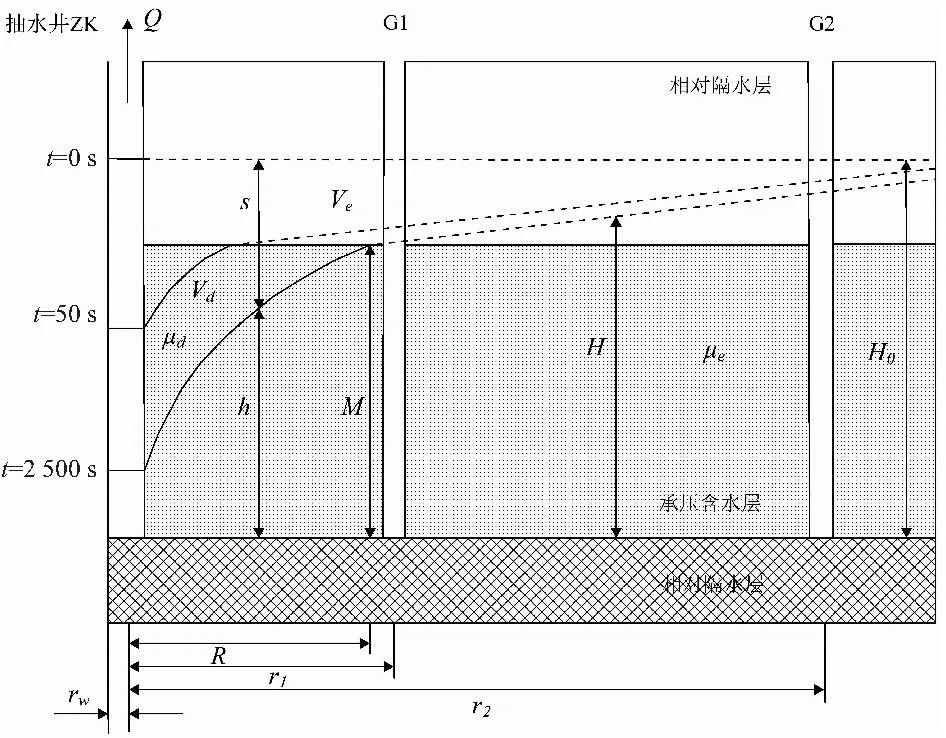
圖7 承壓含水層地下水釋水示意圖Fig.7 Schematic diagram showing the change in groundwater storage of confined aquifer

為了進(jìn)一步分析抽水井附近地下水發(fā)生承壓-無(wú)壓轉(zhuǎn)換對(duì)地下水水位降深-時(shí)間曲線的影響以及泰斯承壓井流模型在承壓-無(wú)壓?jiǎn)栴}上的適用性，繪制了觀測(cè)井G1、G2的地下水水位降深-時(shí)間特征曲線圖并與標(biāo)準(zhǔn)特征曲線進(jìn)行了對(duì)比(見(jiàn)圖8)，特征曲線表示地下水水位降深隨時(shí)間的變化速率。

由圖8可見(jiàn)，觀測(cè)井G1的地下水水位變化特征與雙重含水介質(zhì)或者非承壓含水系統(tǒng)相似[15-16]，在抽水過(guò)程中地下水水位降深隨時(shí)間的變化速率變小而呈現(xiàn)下凹形態(tài)，這表明承壓含水層重力釋水產(chǎn)生的延遲作用，即由于承壓-無(wú)壓轉(zhuǎn)換而存在一個(gè)過(guò)渡期，該時(shí)期內(nèi)承壓含水層無(wú)壓區(qū)重力釋水的增量降低了承壓區(qū)彈性釋水的速度，從而導(dǎo)致地下水水位下降速度變緩，這也對(duì)應(yīng)著圖5中觀測(cè)井G1的s-lgt曲線兩直線段中間的過(guò)渡部分；與觀測(cè)井G1不同，觀測(cè)井G2的地下水水位變化特征圖并未出現(xiàn)下凹段，整體上基本符合承壓含水系統(tǒng)的地下水水位變化特征，說(shuō)明當(dāng)觀測(cè)井距離抽水井較遠(yuǎn)時(shí)，承壓含水層抽水井附近小范圍無(wú)壓區(qū)的出現(xiàn)對(duì)地下水水位變化特征的影響較小，利用泰斯承壓井流模型進(jìn)行承壓含水層水文地質(zhì)參數(shù)求解具有一定的可靠性。

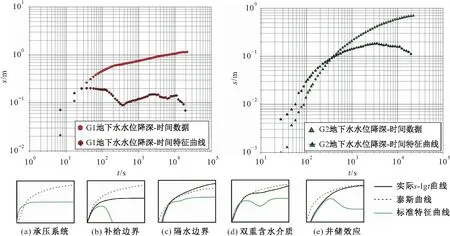
圖8 觀測(cè)井G1、G2地下水水位降深-時(shí)間特征曲線圖Fig.8 Diagnostic diagram of the time-drawdown curve of observation wells G1 and G2

3.2 Chen承壓-無(wú)壓井流模型

陳崇希教授基于吉林斯基勢(shì)函數(shù)，將含水層的導(dǎo)水系數(shù)和給水度分時(shí)段視為空間上的平均值Tm和μm，并近似地視為常量，在含水層的導(dǎo)水系數(shù)T、彈性釋水系數(shù)μe和重力給水度μd已知的情況下，建立了流量、抽水井地下水水位及對(duì)應(yīng)的降落漏斗曲線與時(shí)間之間的函數(shù)關(guān)系，即Chen承壓-無(wú)壓井流模型。Chen模型中地下水承壓-無(wú)壓井流問(wèn)題可描述如下：

(5)

(6)

式中：h、H分別為無(wú)壓區(qū)水位和承壓區(qū)的水頭(L)；H0為初始水頭(L)；R為承壓轉(zhuǎn)無(wú)壓流的徑向距離(L)，即承壓-無(wú)壓轉(zhuǎn)換半徑(L)。

將h=M和r=R代入公式(6)，可得承壓-無(wú)壓轉(zhuǎn)換半徑為

(7)

依據(jù)水均衡原理，抽水量的總體積等于承壓含水層內(nèi)部承壓區(qū)的彈性釋水量和無(wú)壓區(qū)的疏干排水量之和(見(jiàn)圖7)，據(jù)此建立承壓含水層水均衡方程如下：

Qt=μeVe+μdVd

(8)

其中,承壓含水層承壓區(qū)彈性釋水體積Ve為

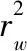
(9)

承壓含水層無(wú)壓區(qū)重力疏干排水體積Vd為

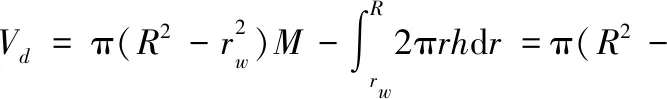
(10)

式中：rw為抽水井半徑(L)。

根據(jù)Chen模型的基本原理可知，當(dāng)已知承壓含水層的導(dǎo)水系數(shù)T和彈性釋水系數(shù)μe時(shí)，根據(jù)承壓-無(wú)壓抽水試驗(yàn)的地下水水位降深變化數(shù)據(jù)可以進(jìn)一步確定承壓含水層的重力給水度μd。具體方法如下：首先將觀測(cè)井G2的地下水水位降深-時(shí)間數(shù)據(jù)(t=1 000～20 000 s)求得的含水層導(dǎo)水系數(shù)T和彈性釋水系數(shù)μe作為含水層真實(shí)的導(dǎo)水系數(shù)和彈性釋水系數(shù)，同時(shí)以在t=20 000 s時(shí)求得的含水層導(dǎo)水系數(shù)和給水度作為空間上的平均值，即取Tm=87.96 m2/d、μm=3.17×10-4，將該組參數(shù)代入公式(7)求取t=20 000 s時(shí)的承壓-無(wú)壓轉(zhuǎn)換半徑R;然后將R代入公式(9)、(10)分別獲得承壓含水層承壓區(qū)彈性釋水體積Ve和無(wú)壓區(qū)重力疏干排水體積Vd；最后將抽水流量Q、抽水時(shí)間t、含水層彈性釋水系數(shù)μe以及Ve、Vd代入公式(8)，最終求得承壓含水層重力給水度μd值為0.197，處于《水文地質(zhì)手冊(cè)》(第2版)中細(xì)砂-砂礫石的重力給水度經(jīng)驗(yàn)值0.15～0.35范圍之間，說(shuō)明該結(jié)果比較合理[18]。

4 結(jié) 論

(2) 泰斯承壓井流模型在一定條件下仍能用于承壓-無(wú)壓井流問(wèn)題并求解承壓含水層的水文地質(zhì)參數(shù)，雖然由于承壓-無(wú)壓的轉(zhuǎn)換會(huì)引起承壓含水層釋水機(jī)理、流場(chǎng)變化特征發(fā)生改變，不滿足泰斯承壓井流模型的假定條件，導(dǎo)致其所求的承壓含水層彈性釋水系數(shù)偏大，但是可以通過(guò)選取抽水后期或者距離抽水井較遠(yuǎn)的觀測(cè)井地下水水位降深數(shù)據(jù)，以盡量降低承壓-無(wú)壓轉(zhuǎn)換的影響，并得到較為可靠的承壓含水層水文地質(zhì)參數(shù)值。