針對隱藏Web數據庫的Skyline查詢方法研究*
李征宇,李 貴,曹科研
1.東北大學 計算機科學與工程學院,沈陽 110004
2.沈陽建筑大學 信息與控制工程學院,沈陽 110168
1 引言
近年來,數據庫Skyline 查詢方法[1-4]得到了廣泛的研究。Skyline 查詢結果也被應用到多目標決策、top-k查詢[5-6]、近鄰搜索(nearest neighbor search)、凸包問題,以及基于用戶偏好查詢等眾多的領域中。例如,利用事先計算的Skyline 可以有效解決基于屬性排序的top-1查詢問題,文獻[5]利用基于Skyline擴展的K-skyband可以有效解決top-k(k≤K)查詢問題。
隨著Web 應用和Web 數據源的迅速增長,通過Web查詢接口來獲取服務端“隱藏”的數據庫Skyline已成為Web數據挖掘領域的一個研究熱點。通過獲取隱藏Web數據庫的Skyline元組可以支持眾多基于Web的第三方應用,比如在Web信息集成中,通過獲取多個隱藏Web 數據庫的Skyline 元組,可以有效地解決滿足用戶偏好的top-k查詢和推薦問題。通過top-k查詢接口來獲取服務器端“隱藏”數據庫的Skyline 面臨著諸多挑戰,其中主要包括:(1)受top-k查詢限制,每次查詢結果最多返回滿足條件的k個元組;(2)用戶選擇的查詢條件受到Web接口類型和屬性類型的限制;(3)用戶端查詢次數受到Web服務器的限制等。基于這些挑戰,如何通過最少的查詢次數獲取服務端隱藏Web數據庫的Skyline的元組成為解決問題的關鍵,目前實現方法有兩種:一是通過Web 查詢接口獲取服務端隱藏Web 數據庫的所有元組,然后在本地生成數據庫的Skyline,這種方式的查詢代價往往很高,同時受到Web 服務端查詢次數的限制;二是通過設計合理的查詢分解算法和對應的查詢條件,通過Web 查詢接口以較少的查詢次數來獲取服務端隱藏Web數據庫的Skyline。文中針對第二種實現方法進行研究,主要貢獻如下:
利用平行坐標系分析Skyline元組折線的相交性質;在定義相交元組查詢分解樹和證明查全性的基礎上提出了Web隱藏數據庫的Skyline元組的啟發式求解方法;并依據Web 接口類型提出了基于混合屬性條件范圍的隱藏Web 數據庫Skyline 元組求解算法;采用離線和在線數據集進行了算法的實驗驗證,通過理論分析和實驗結果表明文中提出的算法在查詢代價和查詢效率方面都優于目前現有的方法。
2 相關研究
Skyline 的概念最初是由Borzsony、Kossmann 等人在文獻[7]提出,隨后研究者基于不同的背景進行了大量的研究工作,其中文獻[8-10]利用索引和預排序技術提出了在線和漸進式的Skyline計算方法。文獻[1]研究以支配分數作為度量,設計了基于表掃描的RSTS(ranked Skyline with table scan)算法來獲取海量數據上有效top-kSkyline 的查詢結果。文獻[2]在交互式多用戶的場景下,研究通過用戶交互動態調節用戶權重,設定滿意度度量,以確定滿意度最大的Skyline 候選集。文獻[3]利用Voronoi 圖解決靜態和動態障礙環境中Skyline查詢的問題。文獻[4]在數據更新頻繁時,研究基于時序支配的數據過濾方法,并提出了基于滑動窗口的ρ-支配輪廓查詢算法。文獻[5]研究了基于K-skyband的top-k查詢算法,文獻[6]研究了top-krepresentative Skylines 問題。文獻[7-9]分別研究了基于流數據、偏序關系、不確定數據和成組技術的Skyline 計算方法。文獻[11]研究了P2P 網絡下不確定數據top-k的近似解法,通過引入Quad-tree 索引,分別根據局部和全局top-k間的關系,以及Skyline和top-k的關系,確定上下界實現空間剪枝,最后通過采樣驗證候選集。上述文獻與Web 數據庫Skyline有關的研究主要體現在top-k查詢方面。文獻[12]關注的是數據流上動態輪廓查詢處理,動態輪廓查詢是Skyline 查詢的一個重要變種,目標對于一個給定的查詢點q,返回在維度上最接近q的所有點。文獻[13]針對Deep Web查詢失效問題,提出了基于top-k和Skyline 的查詢結果過濾方法和基于屬性重要程度和數據源關系圖的漸進式查詢策略。文獻[14]針對Deep Web集成查詢中進行的數據抽樣必須具備先驗知識的問題,提出了ANS(adaptive neighborhood sampling)和TPS(two phase adaptive sampling)兩種免先驗知識的采樣方法,以適用Web 隱藏數據庫的集成查詢。文獻[15]研究了Deep Web數據集成的查詢松弛策略,利用全局數據源關系圖DRG(global database relationship graph)進行松弛查詢,分別用Skyline、top-k方法篩選和排序結果集。文獻[16]針對目標屬性分屬不同站點的情況,研究了漸進式分布Skyline 方法PDS(progressive distributed Skylining),以支持不同類型的Skyline查詢和允許用戶監督指導查詢。文獻[17-18]分別定義了優先和頻繁Skyline點,并分別運用Skyline優先級和Skyline頻繁度這兩個新的度量來降低Skyline 候選集的規模,達到提升k-regret算法的目的。
然而,目前針對隱藏Web 數據庫Skyline 的研究較少,文獻[19]在預知Web數據庫查詢排名函數和獲取所有排序元組的條件下,研究了從多個Web 數據庫獲取Skyline 計算方法。文獻[20]提出了一種基于Web查詢接口類型和屬性類別的混合查詢Skyline算法,但查詢代價高,有些情況會超出爬取整個Web數據庫的代價。
3 Skyline相關概念及性質
3.1 相關概念
隱藏Web 數據庫是指Web 服務器端的數據庫,用戶對其查詢只能通過Web查詢接口(top-k查詢)獲得滿足條件的部分元組記錄。
假設隱藏Web數據庫D具有n個元組,每個元組t有m個屬性,分別記為A1,A2,…,Am。屬性Ai的值域表示為Dom(Ai),屬性值表示為t[Ai]∈Dom(Ai)∪{NULL}(1 ≤i≤m)[15]。
Web 查詢接口依據隱藏Web 數據庫的屬性類型(數值型和分類型)可分為:范圍查詢、分類查詢和混合查詢。其中,范圍查詢基于數值屬性指定范圍條件的查詢,包括單端范圍查詢(如價格<300)和雙端范圍查詢(200<價格<300);分類查詢是指基于分類屬性取一個或多個具體值的條件查詢;混合查詢是指既包括數值屬性的范圍查詢又包括分類屬性的分類查詢。
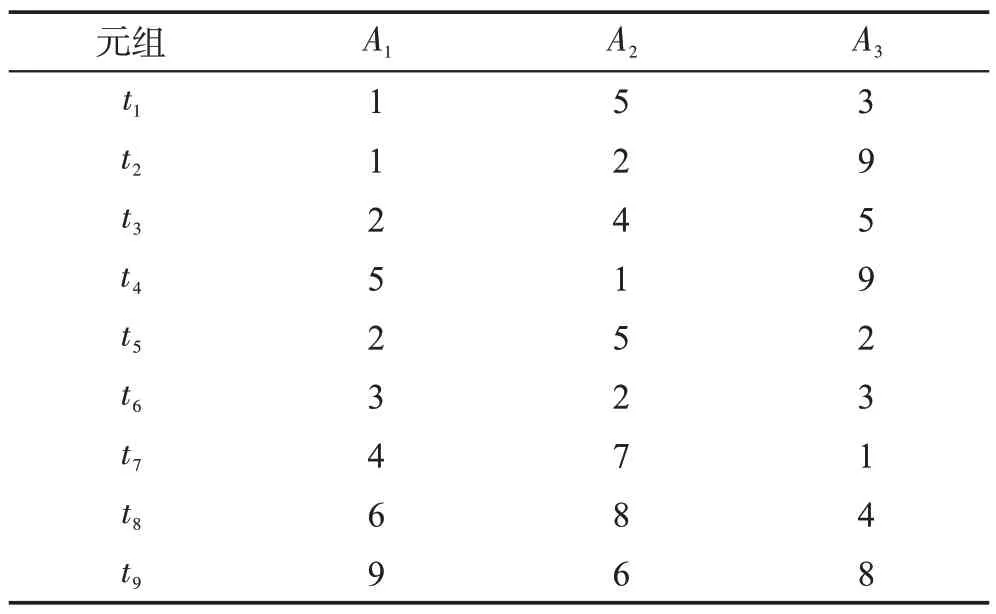
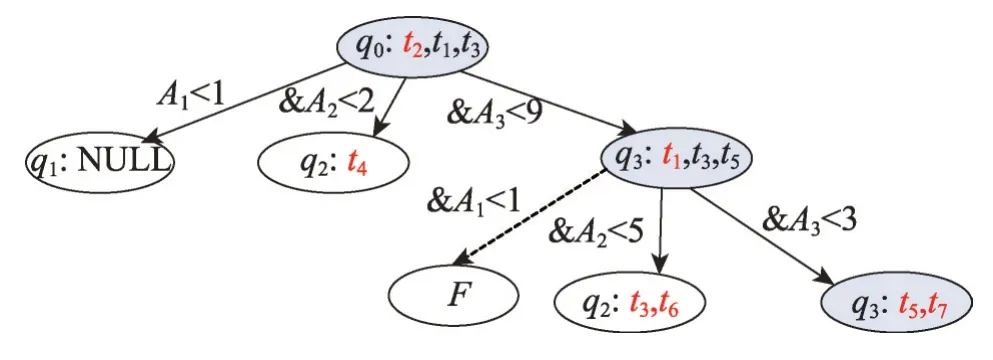
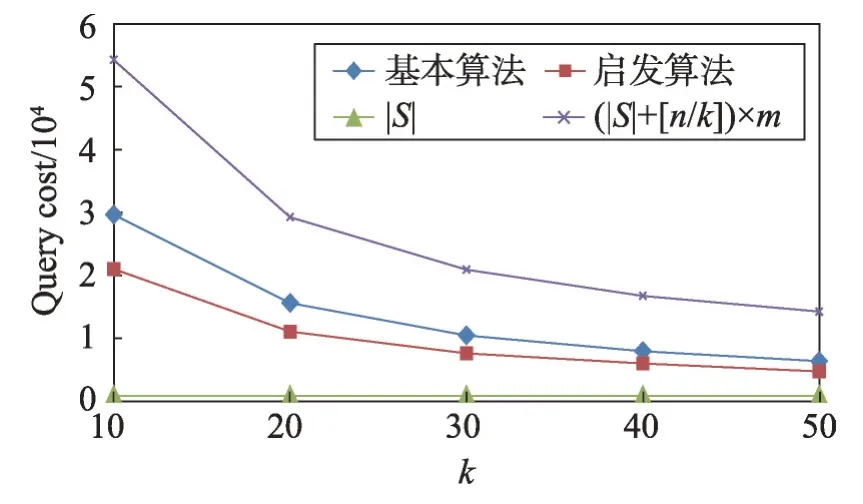
定義1(屬性優先關系)數據庫元組的屬性按其重要程度進行排序,原則是重要的屬性排在前面,次要的屬性排在后面,對于屬性序列{A1,A2,…,Ai-1,Ai,…,Am}來說,Ai-1優先Ai,記為Ai-1 定義2(元組支配關系)兩個元組ti和tj,如果對于任一屬性Ak(1 ≤k≤m),都存在ti[Ak]≤tj[Ak],則元組ti支配tj,元組ti和tj具有支配關系。否則,元組ti和tj是非支配關系。 定義3(元組優先關系)兩個元組tr和ts是非支配關系,如果存在屬性Ak(1 ≤k≤m),使得tr[Ai]≤ts[Ai](1 ≤i 定義4(隱藏Web數據庫Skyline)隱藏Web數據庫D中所有非支配關系的元組構成數據庫D的Skyline,有時也稱為Web數據庫D的輪廓。 定義5(支配一致性約束(dominate consistence constraint))Top-k查詢結果中的k個元組{t1,t2,…,tk}是Web服務器端依據Web接口查詢條件獲得結果元組中受支配最少的k個元組,并依據指定排名函數的元組優先關系“<”排序得到的結果,即ti(1 ≤i 平行坐標系的基本思想是將n維數據屬性空間通過n條等距離的平行軸映射到二維平面上,每一條軸線代表一個屬性維,軸線上的取值范圍為從對應屬性的最小值到最大值,這樣數據庫的每一個元組(或記錄)可以依據其屬性取值而用一條跨越n條平行軸的折線表示(這里要求對空值屬性和分類屬性進行適當處理和映射)。如表1的元組在平行坐標系的表示如圖1所示。 Table 1 Tuples of D表1 D的元組 定義6(相交關系和非相交關系)兩個元組ti和tj(1 ≤i,j≤n)如果存在屬性Ak和Ar(1 ≤k,r≤m,k≠r)使得ti[Ak] Fig.1 Tuple-line diagram of parallel coordinates圖1 平行坐標系的元組折線圖 定義7(完全相交關系)對于任一k個元組,如果其中任何一個元組ti(1 ≤i≤k)和其他k-1 個元組存在相交關系,則這k個元組是完全相交關系。 引理1平行坐標系中任何一個元組支配其上面所有與其非相交的元組。 證明既然任一元組t0和位于其上的元組ti(1 ≤i≤n)都是非相交關系,由定義6 知t0和ti(1 ≤i≤n)均滿足t0[Ak]≤ti[Ak](1 ≤k≤m),再由定義2 可知,t0支配ti(1 ≤i≤n)。 □ 引理2相交關系的元組是非支配關系。 證明若元組ti和tj是相交關系,由定義6 知存在屬 性Ak和Ar(1 ≤k,r≤m,k≠r) 使 得ti[Ak] 定理1一個數據庫的Skyline中所有元組都是完全相交關系。 證明(反證法)假設在數據庫的Skyline中存在兩個元組ti和tj(1 ≤i 定理2在數據庫的Skyline中新增一個元組t,該元組將Skyline劃分成兩部分,和t相交的元組S1,和t不相交元組S2,那么,若t位于S2 下面,則Skyline 由S1和t構成;否則,t必位于S2上面且Skyline保持不變。 證明因為t和S1中的元組均相交,由引理2知,t和S1是非支配關系。此時,若t位于S2下面,由引理1 知,t支配S2,由定義4 可知Skyline 必由S1 和t構成。相反地,若t并不位于S2 下面,假設t出現在S2的中間,那么S2 將被t分成互不相交的兩部分,這和S2 是Skyline 的一部分,由定理1知S2內的元組是完全相交的已知條件相矛盾,故t只可能出現在S2的上方,再由引理1知,S2的所有元組均支配t,最后由定義4知t不是Skyline的組成部分,故Skyline保持不變。□ 假設:查詢qi的top-k結果集T滿足支配一致性約束,結果集T的首條元組為t。 q0:SELECT*FROMD; 依據查詢q0返回結果T,當|T|≥K時,將T的首條元組t遞歸定義如下查詢分解q1,q2,…,qm-1;當|T| q1:WHEREA1 q2:WHEREA1≥t[A1]&A2 q3:WHEREA1≥t[A1]&A2≥t[A2]&A3 …… qi:WHEREA1≥t[A1]&A2≥t[A2]&…&Ai-1≥t[Ai-1]&Ai …… qm:WHEREA1≥t[A1]&A2≥t[A2]&…&Am-1≥t[Am-1]&Am B_Const(t):表示父節點t的分支查詢條件,由根節點到該父親節點的路徑條件的合取組成。如果父節點是根節點,則B_Const(t)=TRUE。 P_Const(qi)=B_Const(t)&A1≥t[A1]&A2≥t[A2]&…&Ai-1≥t[Ai-1]:表示查詢qi查詢的前置條件; 上述查詢可進一步簡化為: q1:WHEREP_Const(q1)&A1 q2:WHEREP_Const(q2)&A2 …… qi:WHEREP_Const(qi)&Ai …… qm:WHEREP_Const(qm-1)&Am 例1假設數據庫D的屬性集和元組集如表1 所示,圖2所示為基于top-3的相交元組查詢分解樹,該查詢樹的所有中間節點都將返回top-3結果的首條元組,相交元組查詢分解的查詢結果是S={t2,t4,t1,t3,t6,t5,t7},從圖2 中可以看出S中的所有元組在平行坐標系中的折線是完全相交關系。 Fig.2 Intersectant tuples query decomposition tree of example 1 based on top-3圖2 例1基于top-3的相交元組查詢分解樹 由上述相交元組查詢分解樹的構造可知其具有如下性質: (1)相交元組查詢分解條件在屬性A1,A2,…,Ai-1,Ai,…,Am-1范圍上是互斥和全覆蓋的。 (2)(相交關系查全性)父節點的首條元組在條件范圍P_Const(qi)下,通過q1,q2,…,qm的m個查詢分解找到的在屬性A1,A2,…,Ai-1,Ai,…,Am上與其有相交關系的最優先元組,分解到最后將找到所有與父節點具有相交關系的元組。 (3)(同一條枝條的完全相交關系)同一條分支上的所有節點元組都具有完全相交關系。 (4)(不同枝條的非完全相交關系)由于查詢條件P_Const(qi)的限制,不同分支上的節點元組可能存在支配關系,即非相交關系或非完全相交關系。 (5)(同層分解的非重復性)由于查詢條件的互斥性,任何節點的查詢分解都不會出現重復元組。 定理3(查全性)如果一個元組t∈D是數據庫D的Skyline 中的一個元組,即t∈Skyline,則在相交元組查詢分解樹中存在一個查詢節點qi,使得該節點的查詢結果T包含元組t(t∈T)。 證明由于t∈Skyline,由定理1 得知,至少存在屬性Ai,Aj(1 t[Ai]>t′[Ai]&t[Aj] 由定義8得知:在相交元組查詢分解過程中將存在一個查詢節點t″(t″∈Skyline) 和一個正整數k(1 t[A1]≥t″[A1]&t[A2]≥t″[A2]&…&t[Ak-1]≥t″[Ak-1]&t[Ak] 即,元組t被包含在節點t″的一個分支節點的查詢結果T中,|T|≥k時,作為首條元組出現。 □ 4.2.1 基本查詢分解方法 依據相交元組查詢分解樹的定義和Skyline元組的完全相交性質,提出如下基本查詢分解方法。 基本查詢分解方法的基本思路[19-20]: (1)通過深度優先或廣度優先方式建立相交元組查詢分解樹,獲得隱藏Web數據庫D中所有具有相交關系的元組集S1和S2,其中S1是查詢分解樹的中間節點的首條元組集合,S2是查詢分解樹的葉子節點的元組集合。 (2)對于S1?S2中的元組,依據Skyline元組的完全相交性質生成隱藏Web數據庫D的Skyline元組集。 4.2.2 啟發式查詢分解方法 為減少查詢代價(遠程查詢次數)提高查詢效率,提出如下啟發式查詢分解方法。 啟發式查詢分解方法的基本思路: (1)在基本查詢分解中,每次查詢分解首先在父節點的返回結果集中進行本地查詢,如果查詢結果非空,則不發出遠程查詢請求;如果查詢結果為空,則發出遠程查詢請求。 (2)如果查詢結果的首條元組t被當前查詢樹的某一節點的查詢結果中的元組t′支配,則將t置換為t′繼續分解。 定理4啟發式分解方法具有查全性。 證明對于啟發式的情況(1),若子節點對父節點的分解結果的本地查詢非空,結果集的首記錄記為t1,那么容易知道該子節點若進行遠程訪問所獲查詢結果亦非空,結果集的首記錄記為t2,由隱藏Web數據庫的支配一致性約束知,t1=t2,故可用非空的本地查詢代替遠程查詢(為確保約束成立,只需保證父節點分解結果中元組出現的先后順序在本地查詢的結果中維持不變)。 對于啟發式的情況(2),將t置換為t′,由于t被t′支配,那么由t′產生的分解樹將更為簡短,因為根據分解樹的生成條件表達式,t′產生的條件表達式中必有一子項比t的上界更低,進而可以更多更快地過濾非Skyline元組,但所剩元組(包括中間節點和葉子節點)所構成的分解樹中包含的Skyline 是不變的。由(1)、(2)知啟發式方法的查全性。 □ 在求解服務端隱藏Web數據庫的Skyline元組時查詢代價的主要因素決定于遠程查詢次數,依據相交元組查詢分解樹的定義得知,遠程查詢次數等于相交元組查詢分解樹中的遠程查詢分支數。 定理5啟發式查詢分解方法的查詢代價C(遠程查詢次數)在K≤m條件下滿足如下不等式: m+1 ≤C<(|S|+[n/k])×m(k≤n) 證明從查詢的分解過程得知:從最初通過Q0=SELECR*FROM D →T0查詢得到的T0的首條元組t1(t1∈Skyline 元組)開始,對t1的每一次分解查詢Qi,首先依據父節點的查詢結果T0執行本地查詢,查詢的結果為Ti: 當Ti≠?時取T中的首條元組繼續m次分解; 當Ti=?時執行遠程查詢; 當遠程查詢結果|Ti| 當遠程查詢結果|Ti|≥K時,再依據Ti的首條元組t1進行m次的查詢分解。 由于在查詢分解過程中,查詢Qi的首條元組有可能被當前S1?S2中的元組支配,因此在查詢分解樹中會存在Skyline 元組被重復分解的情況,但是由于查詢分解條件的屬性范圍是互斥的,因此Skyline元組重復分解的次數一定不會大于[n/k]次。 因此查詢分解樹的中間節點數不會超過|S|+[n/k],查詢樹中總的分支數(每一條分支代表一次查詢)將不會超過(|S|+[n/k])×m。 查詢分解樹中,遠程查詢的次數必然小于查詢樹中總的分支數,即遠程查詢代價C<(|S|+[n/k])×m。 又因為D中至少有一條Skyline 元組,所以遠程查詢代價C≥m+1。 □ 通過模擬實驗和在線真實實驗兩個步驟進行。在模擬實驗部分采用兩個數據庫:學生成績模擬數據庫和實際項目中真實的房地產戶型數據庫,并開發了基于top-k的查詢接口。由于數據庫已經裝載在本地,數據庫的結構特性(實體的屬性類型、數量和關系等)和數值特性(記錄元組個數等)都是已知的,因此可以通過對這些特性值的調節來檢驗算法的查全性,測試它們的查詢代價,以及觀測它們隨不同因素影響的變化趨勢等。在線實驗依據房譜網(http://www.house-book.com.cn)真實網站對算法進行測試。 學生成績數據庫包括10 門課程(包括5 門數值屬性的考試課和5 門分類屬性的考查課)且存儲有100 000條記錄。考試課的成績取值范圍為[0,100],考查課的成績取值范圍為(5-優,4-良,3-中,2-及格,1-差)。房地產戶型數據庫中設置10個屬性,包含5 300余萬條記錄。實驗中選取5個數值屬性和5個分類屬性。 首先,需要驗證基本分解算法和啟發式分解算法的查全性。在對模擬數據驗證成功后,對實際的網絡數據集進行抓取并全部存儲在本地,然后運用本地Skyline求解算法獲取正確的Skyline集,并用此對基本分解算法和啟發式分解算法獲得的結果集進行驗證。結果表明,無論在模擬數據還是實際網絡數據集上,上述兩種算法均滿足查全性,查全性驗證完畢。此處出于完整性,進行必要的說明,不過鑒于查全性不是本文研究的重點,因此相關的實驗內容就不再列出。 然后,比較基本分解算法和啟發式分解算法的查詢代價,也即遠程查詢的次數C。根據查詢代價的理論分析結果m+1 ≤C<(|S|+[n/k])×m(k≤n),考察參數集{m,|S|,n,k}的變化對上述兩種算法的查詢代價C的影響。此處,為了便于比較兩種算法,當考察一個參數影響時,固定了其他3個參數;考慮到普遍性,其他3個參數設定應當令數據集具有代表性。為此,通過分析設定了相關影響因子,以此生成各典型的數據集。主要的因子包括:Skyline 集占全數據集的比例因子,通過它可以生成稠密集、普通集、稀疏集;范圍型字段和枚舉型字段的比例因子,通過它可以生成不同構成的數據集;規模因子,通過它可生成規模不等的數據集。由于待比較的參數較多,相應組合的情形更多,鑒于篇幅,下面僅列出在各類典型設定中4個參數對兩算法影響的代表情形,即包括屬性的影響效果如圖3,Skyline元組數|S|的影響效果如圖4,數據集規模的影響效果如圖5 和top-k中k的影響效果如圖6。 Fig.3 Effect of number of attributes m on query cost圖3 屬性個數m對查詢代價的影響 Fig.4 Effect of number of Skyline tuples|S|on query cost圖4 Skyline元組數|S|對查詢代價的影響 Fig.5 Effect of data set size n on query cost圖5 數據集規模n對查詢代價的影響 Fig.6 Effect of top-k on query cost圖6 top-k對查詢代價的影響 最后,實驗結果表明無論在哪種情況下,啟發式分解算法的代價都要優于傳統的基本分解算法。 通過Web 接口來獲取服務端“隱藏”的數據庫Skyline 已成為Web 數據挖掘領域的一個研究熱點,文中通過引入平行坐標系技術分析了數據庫多維數據的Skyline 元組相交性質,在定義相交元組查詢分解樹和證明查全性的基礎上,提出了隱藏Web 數據庫的Skyline 元組的基本求解算法和啟發式求解方法,并通過理論分析和實驗驗證了方法的有效性。 盡管如此,啟發式算法的實驗中,特別針對各類典型的模擬數據集的實驗中,發現無效的查詢在不同特性數據集中差距巨大,因而在數據集采樣的基礎上分析其特性,進而針對不同類型的數據集設定不同策略,達到進一步減少遠程查詢次數的目的。 此外,在Web 信息集成中,如何通過上述方法來有效地解決基于用戶偏好的top-k查詢和推薦等問題是下一步要研究的內容。3.2 基于平行坐標系的Skyline元組性質

4 隱藏Web數據庫Skyline查詢方法
4.1 相交元組查詢樹的構造及性質
4.2 Web數據庫Skyline查詢方法
4.3 查詢方法代價分析
5 實驗分析
5.1 數據集
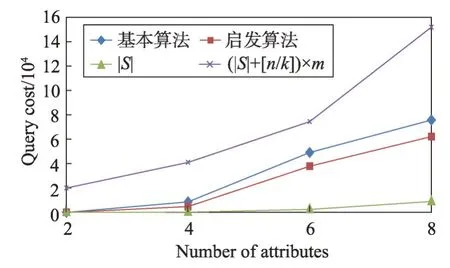
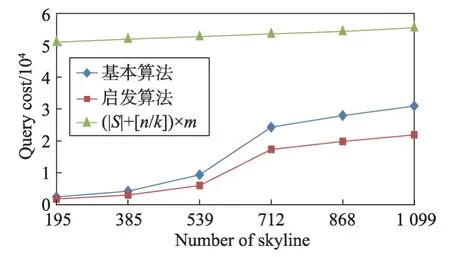
5.2 實驗結果分析

6 結束語

