火眼破偽裝 金睛顯真功

孫偉剛

“平面直角坐標系”的主要學(xué)習(xí)內(nèi)容包括確定平面上物體的位置的方法，平面直角坐標系的建立，平面直角坐標系中點的位置與點的坐標之間的相互轉(zhuǎn)化，坐標方法的簡單應(yīng)用等.本章知識既是將數(shù)軸（一維直線）內(nèi)容向平面直角坐標系（二維平面）內(nèi)容作進一步擴充和延伸，又是今后學(xué)習(xí)函數(shù)圖象、方程和不等式的基礎(chǔ)，更是用代數(shù)方法研究幾何問題的基礎(chǔ)，其地位舉足輕重，為了幫助同學(xué)們更好地鞏固與提升這部分內(nèi)容.特整理出典型問題的“偽解法”，供同學(xué)們潛心研究，深入思考，火眼破偽裝，去粗取精，去偽存真，金睛顯真功.

一、概念太模糊，理解想當(dāng)然

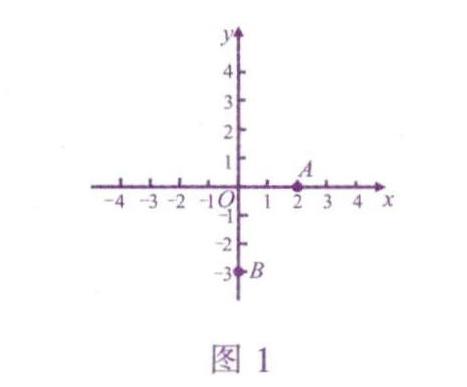
例1如圖1.寫出平面直角坐標系中點A，B的坐標，

錯解：點A的坐標為2.點B的坐標為-3.

【火眼破偽裝】本題要求點的坐標，何謂“點的坐標”？其概念表述為：在平面直角坐標系中，任何一點的位置可以用一對有序?qū)崝?shù)來表示，這樣的有序?qū)崝?shù)對叫作點的坐標.緊抓“點的坐標”的定義，點A、點B釣坐標應(yīng)該都是用一對有序?qū)崝?shù)來表示的，因此錯解中的解答之所以錯誤，原因就不言而喻了.

正解：點A的坐標為（2，0），點B的坐標為（0，-3）.

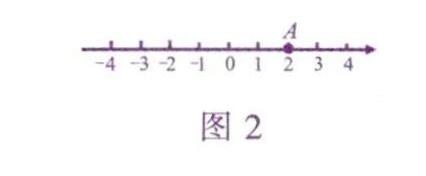
【金睛顯真功】初中數(shù)學(xué)中有大量的概念，它們是數(shù)學(xué)知識的重要組成部分，也是導(dǎo)出數(shù)學(xué)定理和法則的邏輯基礎(chǔ).因此深刻領(lǐng)會數(shù)學(xué)概念特有的內(nèi)涵及外延至關(guān)重要.理解坐標平面內(nèi)“點的坐標”這一概念時，要突出“用一對有序?qū)崝?shù)來表示”這個本質(zhì)特征，并有意與“如圖2.求數(shù)軸上……