基于增量矩陣分解的協同過濾推薦模型研究

樊艷清，李明智，紀佳琪

（1.河北民族師范學院信息中心，承德 067000；2.河北民族師范學院數學與計算機科學學院，承德 067000）

0 引言

大數據時代，推薦系統可以幫助用戶從海量信息中選擇自身感興趣的物品。在眾多推薦模型中，協同過濾以其簡單性及有效性得到了廣泛的應用[1]。協同過濾模型通過對代表用戶喜好程度的“用戶-物品”評分矩陣進行建模，然后計算填充該矩陣中的缺失數據，最后對這些數據進行排行并取出前N條作為推薦結果。在建模中使用的“用戶-評分”矩陣可以分為2類：顯示數據和隱式數據。推薦系統的任務也可以分為2類[2]：評分預測和Top-N推薦。在評分預測任務中，一般使用顯示數據，對用戶評分矩陣中的未知數據進行評分的預測，因此該任務可以轉換為回歸任務。然而收集用戶的評分數據是十分困難的并且是稀疏的，因此很多場景會使用隱式數據。相對于顯示數據隱式數據更好獲取，如用戶的點擊、收藏、購買等都可以看成隱式數據。在這種情況下，“用戶-物品”評分矩陣中存儲的并不是用戶對物品的評分，而是1或0值，分別表示用戶對物品有行為和無行為，此時推薦任務可以轉換成一個二分類任務。

本文主要使用隱式數據解決Top-N推薦問題。在之前的研究中，一般都是獲取到全部訓練數據，然后設計推薦模型[3]。這樣的模型對于用戶興趣改變不大或物品變化不大的場景下比較適用，然而對于一些場景并不適用：如音樂或電影，用戶會隨著時間遷移，其喜好的類型會變化；再如新聞，其更新速度較快，用戶關注點變化也會較快。因此本文不再使用固定數據訓練模型，而是把數據看成數據流，是隨著時間的流逝不斷進入到模型中的，模型要能實時處理這些進入的數據并對其進行訓練，同時實時地更新模型。這類模型稱為增量模型，在數據進入時使用矩陣分解方法，因此本文提出的模型稱為增量矩陣分解的協同過濾推薦模型。

1 相關工作

在推薦系統初期，由于Netflix[4]競賽的盛行，研究者提出了眾多基于矩陣分解的推薦算法，這類算法無論在推薦性能上還是時間復雜度上都優于其他類型的推薦算法。矩陣分解思想最初來源于信息檢索領域的隱語義索引（Latent Semantic Indexing，LSI）[5]方法，LSI使用了奇異值分解（Singular Value Decomposition，SVD）[6]算法對“文檔-詞”矩陣進行分解。在推薦系統領域，矩陣分解（Matrix Factorization，MF）[7]算法借鑒了上述思想，通過對“用戶-物品”評分矩陣進行分解，使得可以用一個隱空間來表示用戶和物品。假設用R表示評分矩陣，P和Q表示分解后的隱空間，即P表示用戶隱空間，Q表示物品隱空間。Pu表示P矩陣中的一行即用戶隱向量，Qi表示Q矩陣中的一列即物品隱向量，表示對矩陣R中u行和i列即用戶u對物品i的預測評分。此時推薦問題可以轉化為公式的優化問題。

其中T表示訓練數據，即用戶對物品的評分數據，λ是正則化參數，||Pu||2+||Qi||2是正則化項用來避免過擬合問題。接下來可以使用梯度下降法（Stochastic Gradient Descent，SGD）對該模型進行優化。對于給定的訓練元組，可以計算預測值與真實值的誤差errui=Rui-，然后可以使用公式進行模型優化求解。

對于矩陣分解模型的算法描述如算法1所示。

算法1：矩陣分解模型算法

輸入：T=，k，iters，λ，η

輸出：P，Q

1. for u Users(T):

2.Pu←Vector∈Rk

3. 取值范圍為（0,1）

4. for i∈Items(T):

5.Qi←Vector∈Rk

6. 取值范圍為（0,1）

7. for count in 1 to iters:

8. forin T:

上述算法是矩陣模型的基本算法，其中T為輸入的訓練數據，k為隱空間的維度，iters為算法的迭代次數，λ為正則化參數，η為學習率。

2 基于增量矩陣分解的協同過濾推薦模型

在上一節描述的矩陣分解模型中，訓練數據是固定，當有新增數據時必須從新啟動模型的訓練，無法適應流式數據，即無法完成在線訓練和實時更新。為了解決這個問題，本文提出了一種增量矩陣分解的協同過濾算法，該模型可以適應流式數據。即當有新數據到來時，不必從新訓練整個模型，而是基于當前數據在已有模型基礎上訓練并實時更新模型。其算法如算法2所示。

算法2：基于增量矩陣分解的協同過濾

輸入：流式數據 T=，k，iters，λ，η

輸出：P，Q

1.forin T:

2.if u?Rows(P):

3.Pu←Vector∈Rk

4.Pu取值范圍為（0,1）

5.if i?Rows(QT):

6.Qi←Vector∈Rk

7.Qi取值范圍為（0,1）

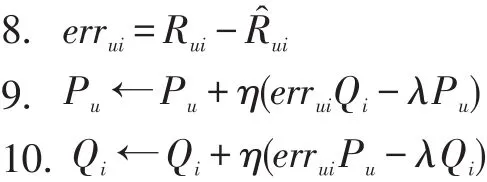
從算法2可見，該模型是一種增量更新方式，當有新的觀測數據到來時就對P和Q進行實時更新。盡管形式上與矩陣分解模型相似，但是其區別也很明顯。首先，當有新數據到來時只對當前數據迭代一次，然后就更新參數P和Q。當然當有新數據到來時對當前數據迭代n次也是可以的，這樣可以獲得相對更好的精度，但是考慮到迭代次數越多消耗的時間越長，而本模型要適應實時在線更新，因此權衡時間和精度等因素后本文還是采用迭代一次的方案，舍棄一點精度的損失來換取時間上的減少。其次，該模型可以是已經經過預訓練的，即利用之前已有的訓練數據做一次全量訓練（利用算法1），然后再做增量訓練（利用算法2）。

算法2中使用的數據為隱式數據，即評分矩陣中的數據要么為1表示正例，要么為0表示負例。此時為0的負例可能有2層含義：用戶不喜歡該物品和用戶對該物品還未有過行為。本文假設為0的負例都是用戶對該物品還未有過行為。這種假設的原因是：可以抽取部分負例參與訓練而不是全部參與訓練。由于數據中只含有0和1，因此誤差的計算可以使用表示。

當迭代完成后，R矩陣中的所有位未知項都已計算完成，此時分別對每個用戶對物品的預測評分值進行降序排序，然后取出前N個物品作為該用戶的推薦物品。

3 實驗

推薦系統常用的評價方法是，把數據集隨機的分成訓練集和測試集，用訓練集對模型進行訓練，用測試集對模型進行評價[8]。然而本文提出的算法并不能使用上述評價方法。主要原因如下：

●數據的順序：由于本文提出的模型要適應流式數據，即數據的到來是有先后順序的，這種順序不能打亂。因此在拆分訓練集和測試集時，要保證其按時間的順序性。

●實時性：本文提出的模型是一種增量更新的模型，當有新的數據到來時，會立即使用這個新數據對已有模型進行再訓練然后更新模型。

因此，本文使用一種能夠適應流式數據的評價推薦系統的方法。首先，我們先使用部分數據對模型進行一個預訓練，形成一個基本可用的模型。然后按照數據生成的時間順序，分別把數據輸入到模型中，然后按照以下步驟進行：

（1）如果user是一個已知用戶（即已經在初始訓練數據集中出現過的用戶），則使用當前模型推薦N個物品給用戶user，否則進入第3步。

（2）對當前的推薦進行評價的計算。

（3）用當前數據重新訓練模型并進行模型更新。

（4）等待下一個（批）數據的到來，然后轉向1。

3.1 數據集

本文使用3個數據集進行模型的評價，其詳細描述見表1。所有的數據集都會處理成按時間順序排列的形式。其中MovieLens①https://movielens.org/是一個經常用于評價推薦系統性能的數據集，其評分范圍從1-5并且含有時間戳信息。Lastfm②https://grouplens.org/datasets/hetrec-2011/是關于用戶聽歌序列的數據集，它有兩個文件，聽歌記錄與用戶信息。MovieT-weetings 10k③http://research.yahoo.com/Academic_Relations來自于Twitter的電影分級數據集，評分值從1-10。

表1 數據集詳情

3.2 結果分析

本文與 ItemKNN（Item-based Collaborative Filtering）[9-10]和 BPRMF（Bayesian Personlized Ranking Matrix Factorization）[11]2個基線算法進行了對比。ItemKNN是推薦系統中較早的模型，目前已廣泛用于工業實踐，因此與之對比有一定的實踐意義。BPRMF是使用矩陣分解方法并取得較好效果的推薦模型，本文也是在其基礎上進行了增量更新的改進。

本文使用召回率（Recall）和模型更新時間（Update Time）作為評價指標。其中Recall@N表示推薦N個物品時的召回率。實驗結果見表2。

表2 實驗結果

從實驗結果可以看出，本文提出的模型在更新時間上明顯快于其他2個模型，在三個數據集上比排在第二的模型分別快10.8倍、25.4倍和7.1倍。召回率上，本文模型在Lastfm和MovieTweetings 10k數據集上明顯高于另外兩個模型。雖然在MovieLens 1M數據集上Recall低于其他兩個模型，但是差異并非很大，與之相對，在更新時間上分別快于其他兩個模型1639倍和10.8倍。因此綜合看來，本文提出的模型在增量更新的性能上明顯優于其他2個模型。

4 結語

目前眾多的推薦模型都是離線完成模型訓練然后上線使用，在積累了一定的新數據后在離線從新進行訓練，為了能夠實時更新推薦模型以適應在線更新，本文提出了一種基于增量矩陣分解的協同過濾模型用于完成Top-N推薦任務。當每次有新數據到來時就進行模型的訓練和更新，使得模型能夠實時應用。在下一步的工作中，我們將比較更多的數據集和更多的基線算法，同時進一步優化已有模型。