高速列車轉向架區(qū)氣動噪聲分離研究*

朱雷威， 郭建強， 趙艷菊， 宋雷鳴

(1.中車青島四方機車車輛股份有限公司 青島，266111) (2.北京交通大學機械與電子控制工程學院 北京，100044)

引 言

轉向架是高速列車最為重要的部件之一，轉向架的各項參數(shù)直接影響著高速列車運行的安全性、穩(wěn)定性和舒適性。列車高速運行時由于空氣氣體壓力變化引起氣體擾動進而產(chǎn)生氣動噪聲，研究表明，高速列車的氣動噪聲與列車運行速度的六次方成正比，當高速列車以超過一定的速度運行時，氣動噪聲將超過輪軌噪聲成為主要噪聲源。氣動噪聲主要來源于轉向架、受電弓、車廂連接處等列車形狀復雜部位[1-4]，從這些部位入手分析研究高速列車的氣動噪聲。

張亞東等[5]建立了高速列車轉向架空氣動力學模型，結合采用定常RNG k-ε湍流模型、非定常 LES 大渦模擬方法、寬頻帶噪聲源模型和 Lighthill 聲學比擬理論來研究轉向架區(qū)域氣動噪聲的相關特性，研究結果得到了轉向架各部件的貢獻量大小以及轉向架遠場氣動噪聲的頻率特性、衰減特性和幅值特性等。李輝等[6]建立了高速列車車廂連接處的簡化模型，通過聲類比理論并結合FLUENT 分析軟件對車廂連接處的氣動噪聲進行了相關分析研究，結果表明車廂連接處端部的圓滑程度直接影響氣動噪聲的大小，端部越圓滑即圓角半徑越大氣動噪聲的數(shù)值就越小。朱劍月等[7]分析了高速列車各主要部位氣動噪聲的形成機理，闡述了氣動噪聲研究的數(shù)值仿真方法和測試技術，并提出了能有效控制高速列車氣動噪聲的措施。高陽等[8]主要研究了高速列車受電弓氣動噪聲的影響，闡述了其產(chǎn)生的機理和降噪措施，對CRH3型車的兩種受電弓結構的縮比模型進行了風洞試驗，并分析對比了受電弓升弓狀態(tài)和降弓狀態(tài)下的氣動噪聲特性。Sassa 等[9]通過試驗方法和數(shù)值計算方法對高速列車車門處產(chǎn)生的氣動噪聲進行了相關研究。Zhang[10]對不同運行速度下列車的輪軌噪聲和氣動噪聲方向性做了相關研究，提出了一個垂直偶極子對模型來解釋輪軌輻射的相關特性。安翼等[11]應用非線性聲學求解器和FW-H聲學比擬法的混合算法，分析研究了高速列車頭型細長比對氣動噪聲的影響，對在不同運行速度下幾種不同頭型細長比的CRH380A高速列車頭型模型進行了試驗分析，得到了不同的流場特征、氣動阻力和氣動噪聲。

以上對高速列車氣動噪聲的研究多數(shù)是采用數(shù)值仿真的方法，建立高速列車縮簡模型作相關的分析以得到氣動噪聲的相關特性。筆者提出一種將高速列車轉向架區(qū)域輪軌、結構噪聲與氣動噪聲分離的方法，將從高速列車在低速運行試驗數(shù)據(jù)求得的傳遞函數(shù)代入到高速列車高速運行時求解貢獻量的過程中，實現(xiàn)氣動噪聲分離的目的。不同于數(shù)值仿真分析方法，此方法是基于工況下傳遞路徑分析(OTPA)方法和聲壓級疊加理論實現(xiàn)的，只需要獲得工況下的實測數(shù)據(jù)即可快速獲得轉向架區(qū)域氣動噪聲對目標響應點的噪聲貢獻。

1 工況下傳遞路徑分析理論

OTPA是一種利用多工況下實測數(shù)據(jù)進行傳遞路徑定量化分析的方法[12-13]。OTPA方法不需要測試靜態(tài)下的傳遞函數(shù)矩陣，較傳統(tǒng)傳遞路徑分析(transfer path analysis，簡稱TPA)方法更為方便，并且能很好地對低頻噪聲貢獻量進行預測[12,14]，因此在軌道車輛噪聲傳遞路徑分析中得到廣泛引用。

通常在測試過程中選取n(n>1)個激勵點，測試m(m≥n)種工況的數(shù)據(jù)，組成一個m維度的線性方程組，其中第j個工況數(shù)據(jù)中目標點處產(chǎn)生的響應為Pj(j=1,2,…,m)，第j個測試步中第i個激勵處的激勵信號為xopji(i=1,2,…,n)，兩者之間的傳遞函數(shù)為hi(i=1,2…,n)，則其矩陣方程[13]為

(1)

其矩陣形式可以簡化為

P=XH

(2)

由于選取的測試工況數(shù)m大于等于激勵源的個數(shù)n，可以保證激勵源信號矩陣的逆矩陣是唯一的。因此在式(2)兩邊同時乘以X的逆矩陣，即可得到傳遞函數(shù)矩陣H，如式(3)所示

H=X-1P

(3)

在測試過程中，不免有干擾噪聲對激勵源測點和目標響應測點產(chǎn)生影響，甚至各個激勵源之間也存在串擾現(xiàn)象。傳感器布置位置盡量接近測試激勵源位置，同時遠離其他激勵源，并對激勵源信號進行奇異值分解，能改善干擾和串擾的影響。

2 轉向架區(qū)氣動噪聲分離理論

2.1 聲疊加原理

n個互不相關的聲源對空間一點T同時作用產(chǎn)生的聲壓大小為

(4)

則在T點的聲壓級大小可通過式(5)得出

(5)

其中：Pi為第i個聲源在測量點T處產(chǎn)生的噪聲聲壓。

假設轉向架區(qū)氣動噪聲、輪軌噪聲和設備噪聲的聲壓級分別為LA，LW和LM，這3類噪聲產(chǎn)生的機理不同，所以這3個聲源互相獨立。

按照式(5)聲壓級相加的計算方法，在這3個聲源作用下，轉向架區(qū)的總聲壓級LG為

LG=10log(100.1LA+100.1LW+100.1LM)

(6)

2.2 氣動噪聲分離原理

高速列車低速運行時，轉向架區(qū)的噪聲主要是輪軌噪聲和由電機、軸箱、齒輪箱等動力設備產(chǎn)生的結構噪聲，氣動噪聲很小，可以忽略不計。采用高速列車低速下的實際測試數(shù)據(jù)，計算出輪軌噪聲與結構噪聲的傳遞函數(shù)。隨著列車速度的提升，輪軌噪聲和結構噪聲的幅值為非線性變化，但其傳遞函數(shù)不隨速度變化而變化。

利用高速下的測試數(shù)據(jù)(200，250，300，350 km/h)作為激勵源數(shù)據(jù)，利用低速下的傳遞函數(shù)求出各個速度下的傳遞路徑貢獻量。該步計算所得貢獻量為各個速度級下轉向架區(qū)域輪軌聲和結構聲的貢獻量，將響應點OTPA合成值與各個速度級下響應點的測試值作比對，再根據(jù)聲壓級疊加公式(6)就可分離出高速下的氣動聲貢獻。

根據(jù)上述選定的激勵源以及目標響應點建立高速列車傳遞路徑分析模型，確定各個傳遞路徑的貢獻量。傳遞路徑和貢獻量分析的傳遞路徑系統(tǒng)(transfer path system，簡稱TPS)計算網(wǎng)絡見圖1。

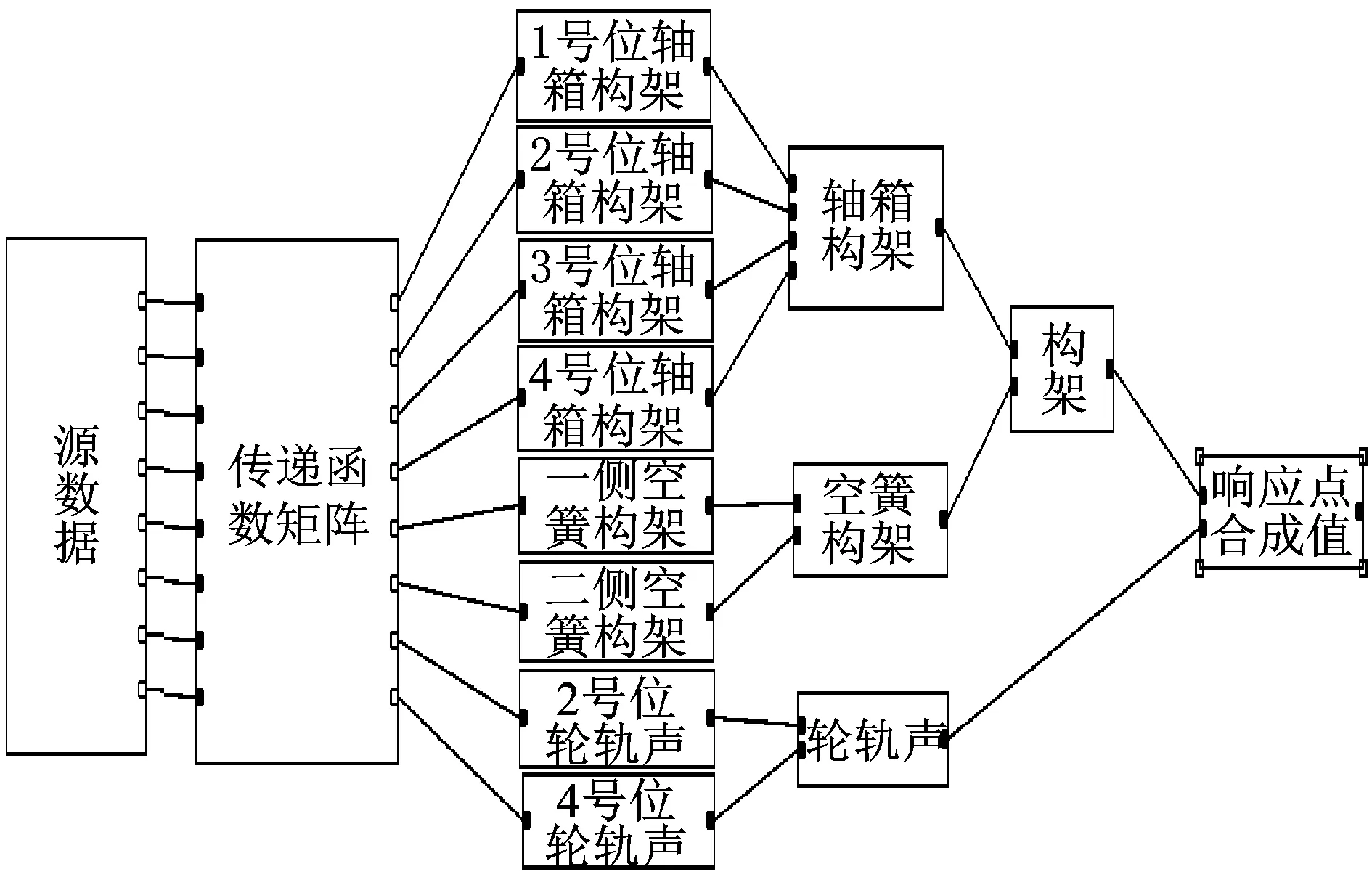
圖1 轉向架區(qū)域傳遞路徑TPS計算網(wǎng)絡Fig.1 TPS computing network of transfer path in bogie area

3 氣動噪聲分離試驗驗證與分析

3.1 傳遞路徑分析試驗

在對高速列車的轉向架區(qū)進行測試過程中，傳感器的布置位置對測試數(shù)據(jù)的精確性以及后續(xù)傳遞路徑的分析結果有著很大的影響。激勵源傳感器的布置要盡量接近測試的激勵源位置，同時保證遠離其他的激勵源，通過傳感器的布置方案來減小甚至消除激勵源間和傳遞路徑間的串擾，保證傳感器測試信號能夠真實有效地反映出被測試的激勵源或路徑本身的噪聲振動特性。

選定轉向架區(qū)域一位端1～4號位軸箱構架、一側及二側空簧構架、2號及4號位輪軌聲作為激勵源測點，以一位端一軸噪聲測點作為目標響應點，圖2為部分測點布置圖。

圖2 部分測點布置圖Fig.2 Arrangement of part of measuring points

3.2 主要測點振動噪聲特性分析

在傳遞路徑分析及氣動噪聲分離前，需對測試數(shù)據(jù)進行前期分析。分別對200，250，300及350 km/h勻速工況下選定的激勵源測點和目標響應測點的噪聲振動特性進行初步分析，確定噪聲振動分布和變化規(guī)律，為后續(xù)的傳遞路徑分析提供數(shù)據(jù)支撐及指導。

在5～350 km/h速度范圍內(nèi)，構架振動加速度隨列車運行速度的提升呈良好的線性關系，如圖3所示。這也說明從低速到高速，構架輻射噪聲傳遞函數(shù)的線性假設，在誤差允許的范圍[±0.01，±0.08]內(nèi)是成立的。

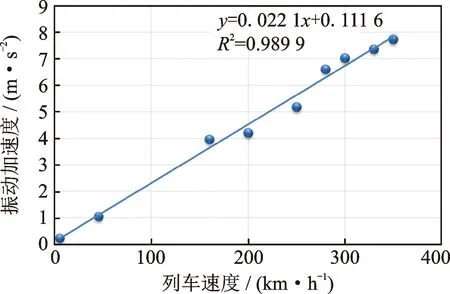
圖3 構架振動加速度隨速度增長趨勢Fig.3 Bogie frame vibration trend with speed growing

圖4分別給出了列車以350 km/h運行時，一位端構架測點的振動快速傅里葉變換(fast Fourier transform,簡稱FFT)頻譜數(shù)據(jù)。各點的振動能量主要集中在800Hz以下頻段內(nèi)，類似位置的測點頻譜特性具有較好的一致性，說明測試數(shù)據(jù)能夠代表該區(qū)域的振動特性。

圖4 350 km/h速度級下構架振動FFT頻譜圖Fig.4 The FFT spectrum of bogie frame vibration under 350 km/h

3.3 氣動噪聲分離結果分析

按照圖1的TPS計算網(wǎng)絡圖進行氣動噪聲分離及求解各個激勵源貢獻量。用高速下(200，250，300，350 km/h)實測數(shù)據(jù)作為源數(shù)據(jù)，以5 km/h速度下求解出的傳遞函數(shù)作為傳函矩陣，可獲得如圖5所示的計算結果。圖中目標響應點的OTPA合成信號小于實測值，兩者的差值即為氣動噪聲的貢獻量。從頻率特性上分析，在1 kHz以下具有較好的吻合性，1 kHz以上則明顯分離，這與結構振動能量主要集中在1 kHz以下、而氣動噪聲峰值出現(xiàn)在1 kHz以上的試驗結果吻合。

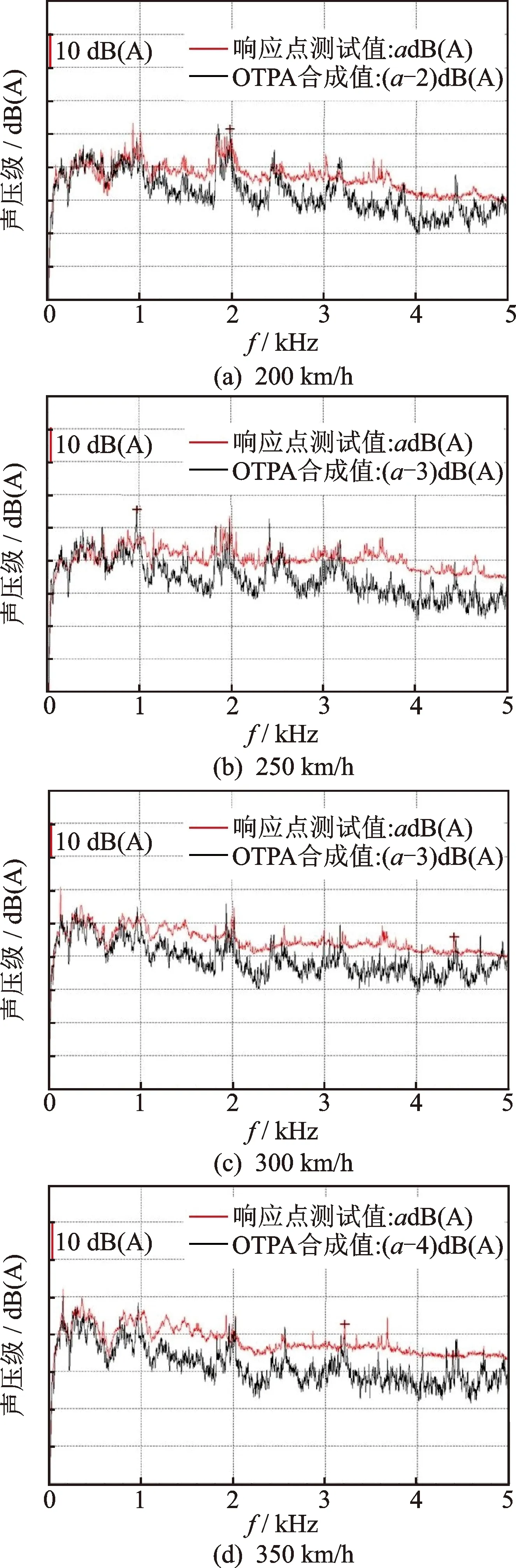
圖5 響應點OTPA合成信號和實測信號Fig.5 The OTPA synthetic signal & measured signal of response points

由式(6)可分離出各速度下氣動聲的貢獻量，下面采用兩種方法對各聲源隨速度增長趨勢進行擬合。

1) 二次多項式法。二次多項式回歸法可以不考慮不同速度級下占主導地位聲源的差異，得到1條在各速度級下均適用的擬合曲線。輪軌噪聲源與速度的3次方成正比，氣動噪聲源與速度的6次方成正比，這種在速度指數(shù)上的區(qū)別導致低速和高速之間并不是線性回歸的關系。經(jīng)過回歸法得到的表達式[15]為

LAeq,Tp=A+Blg(V/V0)+C[lg(V/V0)]2

(7)

其中：LAeq,Tp為通過時間內(nèi)的A計權等效聲壓級(dB(A))；lg(V/V0)為實際速度與參考速度比值的對數(shù)；V為列車速度；V0為參考速度；A，B，C為回歸系數(shù)。

按照上述方法，令橫坐標x為lg(V/V0)，本研究中V0取測試的最低速度160 km/h，在轉向架區(qū)，構架噪聲L1、輪軌噪聲L2、氣動噪聲L3及總噪聲Lb的A聲級隨速度增長規(guī)律,如圖6和式(8)～(11)所示

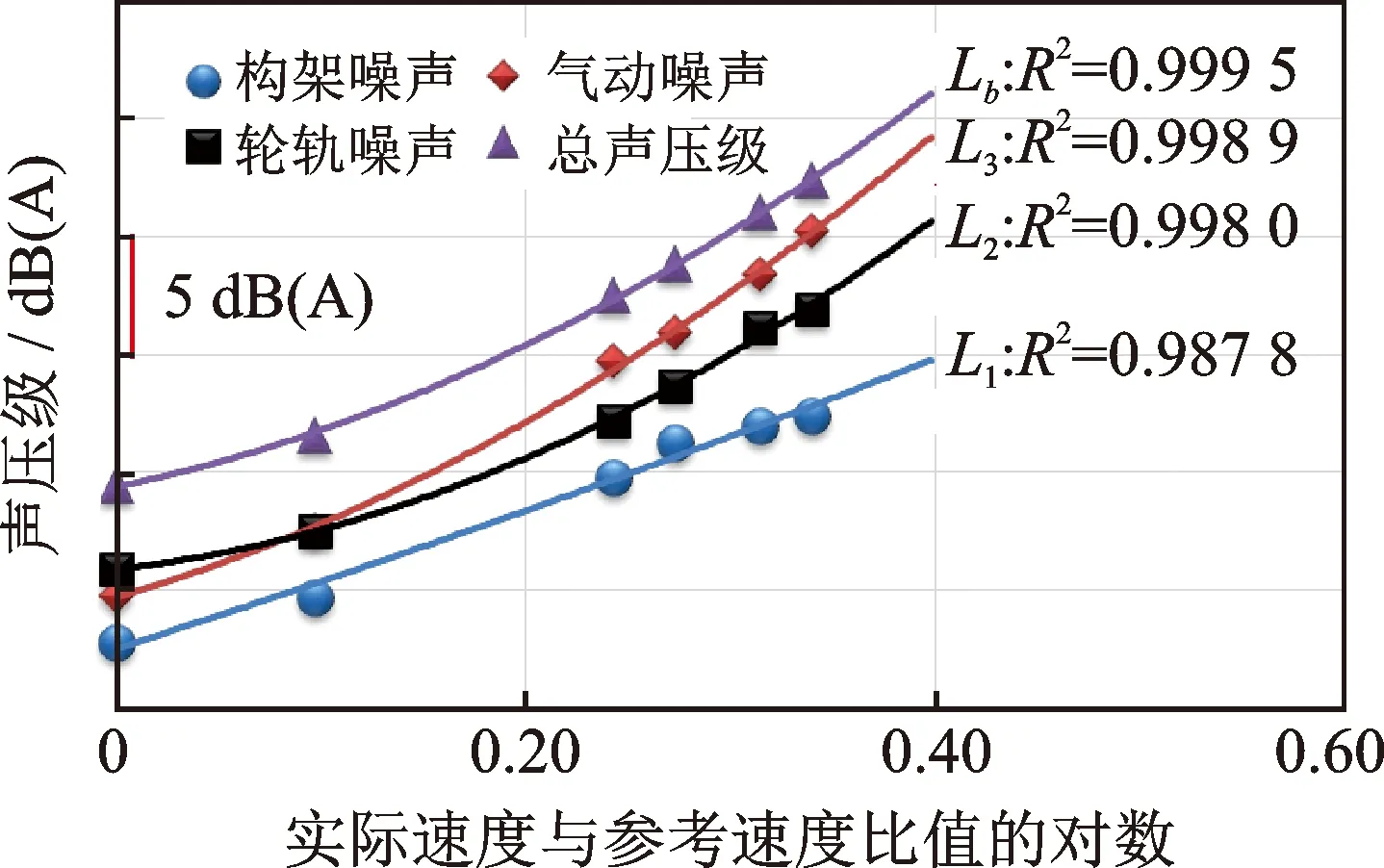
圖6 各聲源隨速度增長的對數(shù)回歸曲線Fig.6 The logarithmic regression curve of each source with speed growing

L1=7.428 5x2+27.744x+102.53

(8)

L2=67.983x2+9.979 9x+105.89

(9)

L3=60.101x2+25.028x+104.72

(10)

Lb=59.447x2+18.191x+109.38

(11)

2) 分段對數(shù)回歸法。二次多項式回歸法雖然能夠得到在各個速度級均適用的公式，但是不便于觀察不同速度級下占主導地位的聲源。分段對數(shù)回歸法得到的公式中，增長率系數(shù)與聲源特性之間有對應的物理意義，可以據(jù)此判斷不同速度級下的主要噪聲源。采用分段對數(shù)回歸法得到的轉向架區(qū)總聲壓級隨速度增長規(guī)律如式(12)、式(13)及圖7所示。從圖中可知，200 km/h以下速度級，轉向架區(qū)噪聲隨速度的3次方增長，以輪軌噪聲為主；300 km/h以上速度級，轉向架區(qū)噪聲大致隨速度的5次方增長，以氣動噪聲為主。

圖7 各聲源隨速度增長的對數(shù)回歸曲線Fig.7 The logarithmic regression curve of each source with speed growing

200 km/h以下速度級轉向架區(qū)總A聲級L200隨速度增長規(guī)律為

L200=30.4lgV+41.9

(12)

300 km/h以上速度級轉向架區(qū)總A聲級L300隨速度增長規(guī)律為

L300=52.7lgV-12.0

(13)

圖8為列車不同速度級下各聲源對總聲壓級的貢獻量。隨著速度的提升，構架聲、輪軌聲與氣動聲的聲壓級均增大。從能量貢獻比例看，氣動噪聲的貢獻量總體呈現(xiàn)逐漸增大趨勢，而輪軌噪聲和構架噪聲的貢獻量逐漸減小。這說明氣動噪聲逐漸占據(jù)主導地位，轉折點出現(xiàn)在200 km/h左右，但即使350 km/h速度級下，氣動噪聲能量比也只占60%，輪軌噪聲的貢獻仍不可忽略。

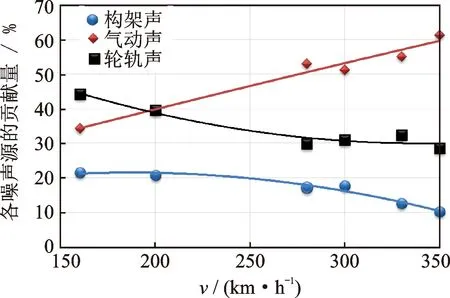
圖8 各聲源貢獻度Fig.8 The contribution of each source

4 結束語

筆者研究了高速列車轉向架區(qū)域氣動噪聲的分離技術，利用低速下(5 km/h)列車運行時氣動噪聲小、可忽略的特點，將低速下求解出的傳遞函數(shù)代入到高速下傳遞路徑貢獻量求解過程，實現(xiàn)了高速下轉向架區(qū)域氣動噪聲的分離，得到了氣動噪聲對目標響應點的噪聲貢獻量。結果表明，隨著速度的提升，氣動噪聲的貢獻量總體呈現(xiàn)逐漸增大趨勢，而輪軌噪聲和結構噪聲的貢獻量逐漸減小，氣動噪聲逐漸占據(jù)主導地位，轉折點出現(xiàn)在200 km/h左右。但即使350 km/h高速運行時，氣動噪聲能量比也只占60%，輪軌噪聲的貢獻仍不可忽略。該研究結論可為高速列車的減振降噪措施及結構優(yōu)化方案設計提供有價值的參考。