變速箱串聯齒輪傳動模態分析與有限元仿真*

王勝曼，唐宇恒

(1.保定理工學院，河北 保定 071000； 2.河北省地礦局第一地質大隊，河北 邯鄲 056000 )

0 引 言

對于齒輪傳動系統，在剛性機械系統的動力學分析中，假設所有構件都是剛體。但是隨著機械運動速度的提高，機械本身重量的減輕和機械工作精度的提高，構件本身的彈性變形成為不可忽略的因素。構件的彈性可以引起運動配合關系失調、降低運動精度、產生機械振動和機件疲勞損壞。在齒輪傳動系統中當傳動軸的長度比較大時，由于軸的彈性變形在機械起動、停車或載荷變化時會出現同一軸上零件運動的不同步或振動現象，從而影響機械的正常工作。因此整個齒輪傳動系統的彈性問題在運行中產生的振動和精度問題是機械系統動力學研究的重點問題。

為了保證變速箱齒輪傳動系統的運轉精度減少振動，近年來不少學者針對此問題展開了機械系統動力學研究。一些學者利用不同的軟件或者實驗方法對其變速箱箱體進行了自由模態或約束模態的動力學仿真，其目的是為了改進箱體的結構設計以便減輕振動[1-7]。還有一些學者把齒輪傳動系統中的一對齒輪嚙合作為研究對象，利用ANSYS或其他軟件進行模態分析，其目的是改善齒輪傳動產生的振動和噪聲[8-10]。還有一些學者把齒輪傳動及變速箱殼體裝配在一起作為研究對象，進行整體結構的模態分析，從而提出改進箱體整體結構的建議，以便減輕機械傳動系統的振動問題[11]。以上這些研究只限于齒輪傳動系統的部分構件的研究，只分析了部分構件的振動特性，沒有對整個齒輪傳動系統進行研究。

馮宇晨,陳艷鋒撰寫的行星齒輪傳動系統接觸模態分析一文中，作者對行星齒輪傳動進行了自由模態和約束條件下兩種模態仿真分析，獲得了行星齒輪系統相應的固有頻率和振型[12]。樊智敏撰寫的帶式嚙合介質齒輪傳動的模態分析一文中，把普通漸開線齒輪傳動系統和帶式嚙合介質齒輪傳動作為研究對象進行模態分析，并對比了兩種仿真結果，發現改變介質帶的彈性模量、泊松比、厚度等可以改變系統的振型[13]。基于Abaquas的齒輪傳動系統模態分析一文中，將系統結構進行離散，使無限自由度問題簡化成多自由度問題。建立了多自由度系統振動的運動微分方程，并利用利用Abaquas軟件對變速箱進行了模態分析[14]。以上研究中研究者大都基于剛性機械系統多自由度動力學理論，采用了不同的研究工具，針對齒輪傳動系統進行機械系統動力學分析，得出來系統的模態振型。但是對于齒輪傳動系統中把軸類構件看作彈性構件進行扭轉動力學系統分析的較少。

1 研究理論基礎

1.1 串聯齒輪傳動系統等效力學模型

對于由N個軸組成的多級串聯齒輪傳動系統，利用拉格朗日方程可以簡化成一單軸系統。

(1) 串聯齒輪傳動系統原始參數

如圖1所示，已知J1,J2,J2′,J3,J3′,J4分別為轉盤的轉動慣量，θ1,θ2,θ2′,θ3,θ3′,θ4分別為轉盤的轉角，K1,K2,K3分別為軸的剛度系數。

圖1 傳動系統簡化力學模型

對于等截面軸，轉角θ、剛度系數K可以采用材料力學中的計算公式進行計算求解。

式中：T為軸的扭矩；L為軸的長度；d為軸的直徑；G為剪切模量；I為極慣性矩[15]。

(2)串聯齒輪傳動系統廣義坐標

6.牛流行熱。急性死亡多因窒息所致。剖檢可見氣管和支氣管黏膜充血和點狀出血，黏膜腫脹，氣管內充滿大量泡沫粘液。

根據圖1(a)所示，θ2和θ2′,θ3和θ3′之間有確定的速比關系：

θ2′=i2′2θ2=i31θ1

θ3′=i3′3θ3=i43θ3

因此θ1,θ2,θ3,θ4相互獨立為廣義坐標，系統的自由度為4。

1.2 串聯齒輪傳動系統動力學方程

采用拉格朗日方程來建立系統的動力學方程。具有完整理想約束的有N個廣義坐標系統的拉格朗日方程的形式是：

(1)

式中：E為系統動能；U為系統的勢能；qr為第r個廣義坐標；Fr為第r個廣義坐標的廣義力[16]。

系統的動能：

E對個參數求偏導數得：

(2)

系統的勢能：

勢能U對各參數求偏導數得：

=-i2′2K2θ2+(K2+K3i3′3)θ3-i3′3K3θ4

(3)

將公式(2)和公式(3)帶入公式(1)中可得：

i3′3K3θ4=0

(4)

對公式(4)廣義坐標進行變換，并進行參數替換得：

(5)

公式(5)為無外力時的動力學方程，圖1(a)和(c)兩個系統具有相同的動能和勢能。

2 串聯齒輪傳動系統三維模型的建立

2.1 串聯齒輪傳動系統各構件的參數

如圖1(a)所示，串聯齒輪傳動系統由帶輪1、齒輪2、齒輪3、齒輪4、齒輪5、滾筒和軸1、軸2、軸3組成。各構件的原始參數見表1、表2所列。

表1 各輪參數表

表2 各軸參數

2.2 串聯齒輪傳動系統各構件材料特性

為了便于分析，串聯齒輪傳動系統各構件均采用優質碳素鋼45，45號鋼為中碳鋼，含碳量為0.45%，一般用于比較重要的機械零部件的材料。見表3所列。

表3 構件材料特性

2.3 模型的建立和網格的劃分

在建模環境下利用UGNX軟件，建立串聯齒輪傳動系統各構件的三維模型。模型完成后在裝配環境下，利用接觸、對齊、距離、平行等約束等命令，對串聯齒輪系統各構件進行約束。帶輪與軸1、齒輪2與軸1、齒輪3與軸2、齒輪4與軸軸2、齒輪5與軸3、滾輪與軸3之間的裝配采用接觸與對齊進行約束；齒輪2與齒輪3、齒輪4與齒輪之間采用接觸、對其、中心距離進行約束，從而完成串聯齒輪傳動系統的裝配工作。在高級仿真環境下，利用NX NASTRAN求解器進行求解。NX NASTRAN求解器模態分析用于計算和評估結構的固有頻率和自然模態即陣型分析，計算時不考慮阻尼，和外載荷也不相關。它提供了跟蹤法、變換法和蘭索士法3種數值解算方法。設置各構件材料屬性，并指派對應材料。創建物理屬性為PSOLID1，網格收集器為SOLID1，單元屬性CTETRA10四面體網格。采用自由網格劃分，單元大小為11.5 mm，單元總數為71 574個。有限元模型如圖1所示，仿真模型如圖2所示。

圖2 串聯齒輪傳動系統三維裝配模型 圖3 串聯齒輪傳動系統有限元模型

3 仿真結果

文中分別對齒輪串聯傳動系統，采取自由模態進行計算和約束模態進行計算。自由模態仿真對象類型分別采用面對面粘接和面對面接觸兩種方案進行仿真計算。

3.1 串聯齒輪傳動自由模態計算結果

解算方案類型為SEMODES-103，子工況特征值法。特征值方法采用Lanczos法，所需數據模態數設置為14。仿真對象類型為面對面粘接，搜索距離為1mm，共創建17個面對。在無約束下狀態下進行模態仿真。在[后處理導航器]窗口中，可以發現仿真計算結果的前6階模態非常接近零，因為本次計算的是齒輪系統的自由模態，放開了6個自由度，在6個自由度方向中出現了剛體位移。仿真結果如表4和表5所列，串聯齒輪傳動系統非零后8階模態見圖4所示。

表4 非零后6階模態頻率及振型

表5 非零后6階模態頻率及最大應力

圖4 串聯齒輪傳動系統非零后8階模態

從以上仿真數據可以看出，軸1、軸2、軸3的剛度嚴重不足，在各階振型下發生了較大變形，且在各軸端部應力最大。如果激勵頻率與系統固有頻率接近時發生共振，各軸將是最薄弱環節。同時各軸的較大變形，將嚴重影響系統的運轉精度。因此在軸的端部施加支座或增加質量，將改善軸的振型，提高系統的穩定性。

3.2 串聯齒輪傳動等效模型模態計算結果

根據等效模型力學公式進行計算各軸的等效剛度和各輪的等效轉動慣量，并將等效剛度進行逆運算，在各軸長度不變的情況下，等效為各軸的直徑尺寸(見表6所示)。將等效轉動慣量按照逆運算，在各輪寬度尺寸不變得情況下，等效為各輪的直徑。(見表7所示)根據表6和表7中的尺寸，在UG建模環境下進行三維模型的建立并完成裝配。在高級仿真環境中，設置各構件材料屬性，材料同上，并指派對應材料。創建物理屬性為PSOLID1，網格收集器為SOLID1，單元屬性CTETRA10四面體網格。采用自由網格劃分，單元大小為19.8 mm。解算方案類型為SEMODES-103，子工況特征值法。特征值方法采用Lanczos法，所需數據模態數設置為12。仿真對象類型為面對面接觸，搜索距離為1 mm，共創建10個面對。在無約束下狀態下進行模態仿真。在[后處理導航器]窗口中，查看非零后6階模態頻率及振型，見圖6所示。仿真結果見表8和表9所列。

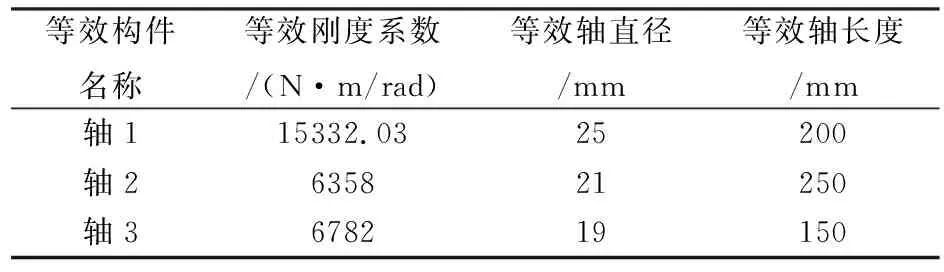
表6 等效模型各軸參數

表7 等效模型各輪參數

表8 兩種模型非零后6階自由模態頻率、最大變形量及最大應力數值表

圖5 兩模型前6階振動頻率

圖6 兩模型前6階最大變形量

通過表8中的數據可以得出，原模型自由模態數據和等效模型自由模態數據在非零后前2階振型頻率非常接近。原模型第7階模態頻率為67.97 Hz，等效模型第7階模態頻率為67.89 Hz。原模型第8階模態頻率為67.34 Hz，等效模型第8階模態頻率為67.89 Hz。這兩階自由模態數據與研究理論相符。從第9階開始，原模型模態頻率與等效模型模態頻率，開始出現差異。第12階原模型模態頻率遠遠低于等效模型模態頻率，仿真結果與研究理論出現偏差。

4 分析與討論

在進行串聯齒輪傳動動力學理論研究時，對系統進行了簡化。

(1) 系統忽略了軸的質量，將軸看看成無質量的扭簧。實際中軸的幾何尺寸越大，軸的質量也越大，軸的轉動慣量也越大。因軸的質量被忽略，因此對振型產生了影響，影響了計算精度。

(2) 系統模型認為支撐是剛性的，不考慮軸的彎曲變形和縱向變形。本文進行了串聯齒輪傳動系統的自由模態分析，沒有對各構件進行約束限制，因此在仿真的過程中，軸的彎曲變形或縱向變形對仿真結果產生了一定的影響。

(3) 系統模型忽略了傳動機構內部的彈性，將各軸之間的傳動比看作常數。實際中齒輪之間的嚙合傳動，在嚙合面上因齒面受力作用，會發生一定范圍內的彈性變形。在系統簡化中將其看作剛體，實際仿真結果與研究理論有一定的差距。

5 結 論

本文首先利用拉格朗日方程對對串聯齒輪傳動系統進行了機械系統動力學模型的建立和理論計算，并將其原模型轉化為等效系統模型。為了驗證理論的正確性，筆者利用UGNX軟件對其原模型和三維模型分別建模并裝配，在高級仿真環境下進行仿真運算。并將兩者結果進行比較，發現非零后前2階即第7階和第8階兩者自由模態振型和頻率一致，符合研究理論。后四階兩者振型頻率有一定的誤差。此研究結論為齒輪傳動系統振動分析與研究提供了理論參考。