附加慣性項神經網絡云臺自抗擾控制研究

劉欣 羅曉曙

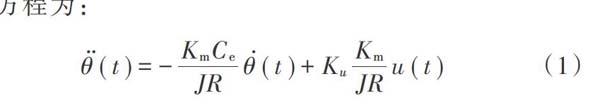
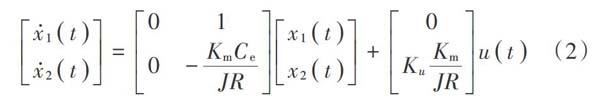
摘? 要： 針對自抗擾控制器參數較多且不易整定的缺陷，以三軸增穩云臺內框為研究對象，提出一種附加慣性項神經網絡云臺自抗擾控制方法。該方法首先通過添加附加慣性項的RBF神經網絡對被控對象進行辨識，從而獲得單神經網絡自學習需要的Jacobian信息，然后將擴展的積分系數、非線性誤差反饋控制律中的比例系數和微分系數作為單神經元的權重，利用單神經元的自學習能力改進自抗擾控制器。仿真結果表明：加入神經網絡的自抗擾控制器具有較好的魯棒性，與參數固定的常規自抗擾控制器相比具有更高的精度和更快的響應速度。

關鍵詞： 神經網絡云臺; 自抗擾控制; RBF神經網絡; Jacobian信息; 收斂速度; 魯棒性測試

中圖分類號： TN876?34; TP273? ? ? ? ? ? ? ? ? ?文獻標識碼： A? ? ? ? ? ? ? ? ? ? ? 文章編號： 1004?373X（2020）03?0154?04

Research of tripod head active disturbance rejection control

based on neural network with additional inertia item

LIU Xin， LUO Xiaoshu

（College of Electronic Engineering， Guangxi Normal University， Guilin 541004， China）

Abstract： In view of the defects that there are too many parameters for the ADRC （Active Disturbance Rejection Control） and it is difficult to adjust them， a method of tripod head active disturbance rejection control based on neural network with additional inertia item is proposed. The inner frame of the triaxial stabilizer is taken as the research object in the research. In the method， the controlled object is identified by adding RBF （Radial Basis Function） neural network with additional inertia item to obtain the Jacobian information needed by single neural network self?learning， and the extended integral term coefficient， the proportional coefficient and differential coefficient in the NLSEF （Nonlinear State Error Feedback） control law are taken as the weights of single neuron， and then the self?learning ability of single neuron is used to improve the ADRC. The simulation results show that， in comparison with the conventional ADRC with fixed parameters， the ADRC with neural network has better robustness， higher accuracy and faster response.

Keywords： neural network tripod head; ADRC; RBF neural network; Jacobian information; convergence rate; robustness test

0? 引? 言

三軸增穩云臺是保證獲得高質量影像的重要裝置[1?3]。傳統的云臺控制系統采用經典的PID控制，但在復雜的環境中，由于外擾突變，傳統的PID不能很好跟蹤突變量的變化，造成控制系統控制精度下降和響應速率減慢[4]。文獻[5]提出將自抗擾控制器（Active Disturbance Rejection Control，ADRC）應用于三軸機載增穩云臺的控制系統，驗證了ADRC比PID具有跟蹤速度更快，抗擾能力更強等優點，但未克服ADRC參數較多難以整定的缺陷。文獻[6]提出了一種采用BP神經網絡對自抗擾控制器中的非線性擴張狀態觀測器進行參數整定的方法，應用于機載光電穩定平臺控制，顯著地提高了擾動隔離度。

本文首先采用RBF神經網絡對被控對象進行辨識，從而獲得單神經元自學習需要的Jacobian信息，以實現參數自整定;通過添加附加慣性項加快RBF神經網絡的收斂速度，提高Jacobian信息的近似程度;然后使用單神經元改進ADRC的非線性狀態誤差反饋（Nonlinear State Error Feedback，NLSEF），通過在NLSEF中增加擴展的積分項，并將此擴展的積分項系數、NLSEF中的比例系數和微分系數作為單神經元的權重，構造具有參數自整定的改進自抗擾控制器，應用于增穩云臺控制系統，以期提高控制精度和響應速度。

1? 云臺伺服系統動力學方程

三軸增穩云臺在空間結構上由三個互相獨立且互相垂直的框架構成，具有三個方向的自由度且三個軸的工作原理基本相同，結構上主要由外框、中框、內框組成[7]。以用于搭載相機的內框為例，建立其伺服系統動力學方程為：

式（1）可轉換為狀態方程，如下式所示：

式中：[Km]為電機力矩系數;[Ce]為電壓反饋系數;[J]為三軸云臺內框的轉動慣量;[R]為電樞電阻;[Ku]為PWM功率放大器放大系數;[u（t）]為控制輸入;[x1t=θt]，為伺服電機轉角;[x2t=θt]為伺服電機轉速。

2? 自抗擾控制理論

文獻[8]分析并指出ADRC可以實現跨階控制，擴張觀測器（Extended State Oberver，ESO）輸出的二階導數不加入外環的非線性組合仍然能保證系統的穩定性。ADRC主要由跟蹤?微分器、擴張狀態觀測器、非線性狀態誤差反饋三部分構成[9]。

以下為非線性狀態誤差反饋方程：

式中：[θ′d]是指令的跟蹤，即安排的過渡過程;[θd]是指令的近似微分;[β1]和[β2]是NLSEF兩個控制參數，類似于PD控制中的[kp]，[kd];[z1]是輸出信號的估計;[z2]是輸出信號微分的估計;[z3]是總擾動的估計;[fal（?）]是非線性函數，其余各參數及各函數的具體意義參見文獻[10]。

3? 基于附加慣性項的RBF神經網絡的云臺動力學系統辨識

RBF神經網絡是具有單隱含層的3層前向網絡，而且是局部逼近的網絡，學習速度快且能克服局部極小值等問題，能滿足實時控制的要求。結合特定被控對象，經反復試湊選取輸入層節點數為3、隱含層節點數為5，輸出層節點數為1的RBF神經網絡。

令被控對象第[k]時刻的輸出為[θ（k）]，神經網絡的輸出為[ym]，取辨識器的性能指標函數為：

根據梯度下降算法，輸出權值[w]、節點基寬參數[b]、節點中心[c]的迭代算法如下：

式中：[i=1，2，3];[j=1，2，3，4，5];[η]為學習速率;[α]是動量因子;[β]是附加慣性項系數;其余各參數及函數的具體意義參見文獻[8]。

將被控對象的輸出對輸入的敏感度稱為Jacobian信息，其值可以通過RBF神經網絡在線辨識獲取，其算法為：

4? 附加慣性項神經網絡云臺自抗擾控制方法

附加慣性項神經網絡改進自抗擾控制器主要由RBF神經網絡辨識器（RBF Neural Network Identifier，RBFNNI）、跟蹤?微分器、擴張狀態觀測器、改進的非線性狀態誤差反饋四部分構成，其結構如圖1所示。其中，[z-1]是延遲算子。RBFNNI對被控對象進行辨識，從而獲得改進的NLSEF中的單神經元自學習所需要的Jacobian信息。

擴張狀態觀測器對總擾動估計的速度與精度會影響到補償后的系統與理想“積分串聯標準型”的接近程度。本文提出在NLSEF中引入擴展的積分項，以期減小當擴張狀態觀測器不能完全實時準確地估計總擾動時系統穩態誤差。通過將[θe]和[θe]進行狀態轉換，得到NLSEF的比例項[x1（k）]、微分項[x2（k）]、擴展的積分項[x3（k）]，再將[x1（k）]，[x2（k）]，[x3（k）]作為單神經元的輸入，控制參數[βi（i=1，2，3）]作為單神經元的權重，以此構造改進的非線性狀態誤差反饋，各控制參數可以通過單神經元的自學習功能進行自整定，其結構如圖2所示。

其中：

式中：[G]是增益系數，需適當選取;[α5]可選取為大于[α4]的數。

取性能指標函數[Je=0.5e2（k）]。加權系數的調整量為：

單神經元權值更新迭代算法如下：

式中：[η1]，[η2]，[η3]為加權系數對應的學習速率;[?ym（k）?u（k）]為RBF神經網絡在線辨識獲取得到的Jacobian信息;[σ]是動量因子。

5? 仿真及結果分析

為研究基于附加慣性項神經網絡云臺自抗擾控制的性能特點，依次使用常規ADRC、神經網絡改進ADRC分別在Matlab仿真環境中進行仿真分析。選取ADRC參數如下：[h=0.001]，[h0=0.001]，[δ1=0.002? 5]，[α1=0.5]，[α2=0.25]，[δ2=2h]，[α3=0.75]，[α4=1.5]，[α5=2]。給定正弦信號指令為[θd（t）=sin（2πt）]，觀察并對比系統在常規ADRC控制下和本文提出的改進ADRC控制下的正弦響應。

系統在常規ADRC控制下的正弦響應如圖3所示，位置跟蹤誤差曲線最大峰值為0.08 rad。基于附加慣性項神經網絡改進ADRC控制的正弦響應如圖4所示。位置跟蹤誤差曲線最大峰值穩定在0.035 rad，這是因為當ESO不能完全實時準確地估計總擾動時，擴展的積分項減小了穩態誤差，神經網絡的引入提高了ADRC的自適應性，所以本文提出的改進ADRC具有較常規ADRC更高的精度。

圖5顯示添加附加慣性項RBF網絡比未添加附加慣性項的RBF網絡具有更快的收斂速度，可以到更好的逼近效果，能夠提高Jacobian信息的近似度。

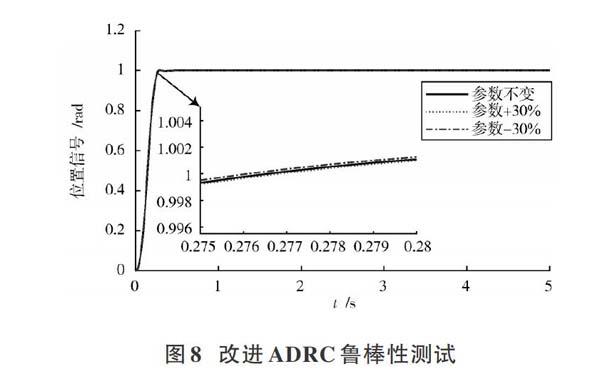
圖6為在指令為單位階躍信號時，單神經元各權重自適應調整曲線。圖7和圖8為系統的魯棒性測試，實驗方法是將轉動慣量增加和減少30%，測試系統的單位階躍響應。由于ADRC本身就具有較好的魯棒性，所以兩者的魯棒性從整體上看差別不大。由局部放大對比可知，兩者的超調量均約為0.2%，常規ADRC的上升時間為0.284 s，改進ADRC上升時間為0.276 s，在超調量相同的情況下改進ADRC比常規ADRC具有更快的響應速度。

6? 結? 語

本文以三軸增穩云臺內框為研究對象，利用神經網絡的自學習能力對常規自抗擾控制器進行改進，提出一種附加慣性項神經網絡云臺自抗擾控制方法，實現了具有參數自整定能力的改進ADRC，減少了控制器調整參數，提高了ADRC的自適應性。仿真及實驗結果表明，該控制器具有較好的魯棒性，與參數固定的常規ADRC相比具有更高的精度和更快的響應速度，具有較好的工程應用價值。

參考文獻

[1] 郭炳坤，陳水利，吳云東，等.無人機三軸穩定云臺的模糊PID控制[J].集美大學學報（自然科學版），2013，18（4）：308?313.

[2] 林峰，王曉曉，曲曉光.四旋翼無人機航拍云臺的控制系統設計[J].沈陽航空航天大學學報，2016，33（5）：55?60.

[3] 王日俊，曾志強，黨長營，等.一種基于STM32的機載慣性穩定云臺的設計[J].現代電子技術，2018，41（12）：145?148.

[4] 馮志剛，舒林.基于ARM的航拍三軸云臺控制系統設計與研究[J].沈陽航空航天大學學報，2017，34（3）：70?75.

[5] 要亞忠.三軸機載增穩云臺ADRC控制的研究及應用[D].哈爾濱：哈爾濱工業大學，2017.

[6] 朱啟軒，張紅剛，高軍科.光電穩定平臺神經網絡自抗擾控制方法[J].電光與控制，2018，25（3）：10?14.

[7] 舒林.基于ARM的航拍三軸云臺控制系統設計與研究[D].沈陽：沈陽航空航天大學，2018.

[8] 王濤，楊曉萍，余向陽，等.基于神經網絡的水輪機調節系統自抗擾控制[J].水力發電學報，2006，25（3）：125?129.

[9] 任潞，何屏，張曉磊，等.基于PSODE混合算法優化的自抗擾控制器設計[J].現代電子技術，2017，40（3）：92?95.

[10] 孫金秋，游有鵬.基于線性自抗擾控制的永磁同步電機調速系統[J].現代電子技術，2014，37（16）：152?155.