基于優化神經網絡的音樂分類模型研究

黃璟

摘? 要： 為高效、精準地判斷音樂風格歸屬，幫助用戶快速獲取偏好音樂風格，基于群智優化神經網絡構建音樂風格分類模型。提取音樂樣本的音質、節奏、旋律特征作為模型訓練樣本輸入BP神經網絡，通過初始化、隱含層及輸出層計算、權值計算等步驟完成神經網絡模型訓練。采用粒子群算法確定神經網絡的最優權值與閾值，粒子群算法首先編碼神經網絡權值與閾值，其次計算粒子適應度值，更新粒子速度和位置，符合終止條件時輸出神經網絡的權值與閾值優化結果，并據此構建基于群智優化神經網絡的音樂風格分類模型。模型測試結果表明，所提模型在正確區分不同音樂風格的同時，展示了音質、節奏、旋律等特征。

關鍵詞： 音樂分類; 分類模型; 特征提取; 模型訓練; 最優權值確定; 模型構建

中圖分類號： TN911.1?34; TP181? ? ? ? ? ? ? ? ? ?文獻標識碼： A? ? ? ? ? ? ? ? ? ? 文章編號： 1004?373X（2020）03?0096?04

Research on music classification model based on optimal neural network

HUANG Jing

（Music Department， Putian University， Putian 351100， China）

Abstract： In order to efficiently and accurately judge the type of music style and help users quickly obtain their preference for music style， a music style classification model was built based on swarm intelligence optimization neural network. The acoustic quality， rhythm and melody characteristics of music samples are extracted as model training samples and input into BP neural network. The neural network model training is completed after the steps of initialization， hidden layer and output layer calculation， weight calculation and so on. The particle swarm algorithm is adopted to determine the optimal neural network weight and threshold， and then code the neural network weight and threshold， and calculate particle fitness value to update the particle velocity and position. When they conform to with the termination conditions， the optimization results of the neural network weight and threshold are output. On the basis of the results， the music style classification model based on swarm intelligence optimization neural network is constructed. The model testing results show that the model can correctly distinguish different music styles， and exhibits the characteristics of sound quality， rhythm and melody.

Keywords： music classification; classification model; feature extraction; model training; optimal weight determination; model building

0? 引? 言

當代互聯網技術高速更新，移動終端設備使用人群規模迅速增加，流行音樂傳播方式從電臺和唱片形式逐漸過渡到網絡電臺在線收聽和互聯網下載等形式。相關調查顯示，65%用戶難以精準獲取期待收聽的歌曲或不明確自身音樂風格喜好。網絡電臺通常依照用戶對音樂風格的喜好推薦歌曲，用戶喜好的音樂類型可能包含多種音樂風格，導致待分類音樂規模較大，音樂分類難度大。因此，采用一種智能方法實現音樂風格分類十分重要[1]。流行音樂傳統分類包括流行、鄉村、爵士、搖滾、節奏布魯斯、新世紀等六大類別，每一大類劃分成不同小類，部分小類還可以進一步劃分[2]。依靠人為方式劃分音樂風格存在很多弊端，如分類效率低、音樂風格歸屬判斷困難大、音樂風格類別過于粗糙或者過于精細等[3]。因此，亟待研究一種音樂風格分類模型，采用合理方法解決音樂風格分類問題。

群體智能優化算法簡稱群智優化算法，群智優化算法中最知名的是粒子群算法[4]。本文采用典型的BP神經網絡構建音樂風格分類模型，利用粒子群算法改進BP神經網絡，確定神經網絡最優輸入權值與閾值，避免網絡隨機性，解決神經網絡訓練時間長、陷入局部最優解的缺點，構建智能的音樂風格分類模型。

1? BP神經網絡音樂風格分類模型

1.1? 訓練樣本處理

選擇流行音樂作為神經網絡訓練樣本數據，涵蓋六種音樂風格。根據音樂信號提取音樂的音質、節奏、旋律特征，音質特征體現音樂信號的紋理特性;節奏特征體現音樂信號時序性，反映音樂動態韻律信息;旋律特征體現音樂曲調輪廓，描述音樂風格基本情況。將上述特征作為神經網絡訓練的輸入樣本。

1.2? BP神經網絡結構

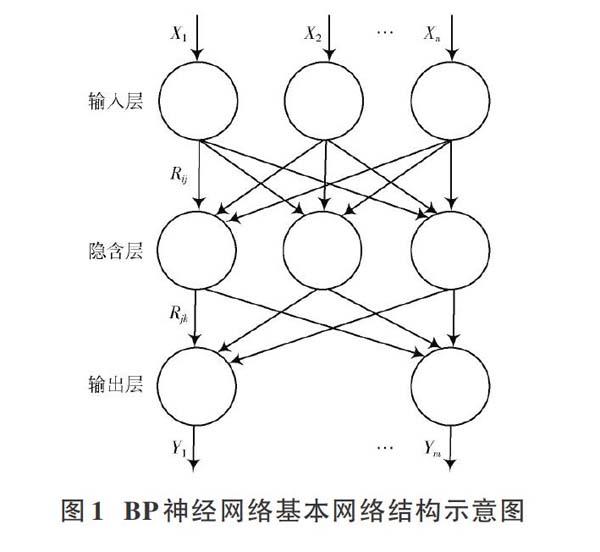
BP神經網絡是由輸入層、輸出層以及隱含層構成的一種多層前饋神經網絡[5]。BP神經網絡中各層次神經元之間全面連接，同一層次神經元彼此無連接。BP神經網絡基本網絡結構如圖1所示。BP神經網絡輸入向量數量用[n]表示，輸入向量用[X]表示，其中，[X=（X1，X2，…，Xn）]。BP神經網絡輸出向量數量用[m]表示，輸出向量用[Y]表示，其中[Y=（Y1，Y2，…，Ym）]。

1.3? BP神經網絡訓練步驟

BP神經網絡訓練步驟如下：

1） 網絡初始化

明確BP神經網絡拓撲結構，選擇[n]，[d]，[m]分別作為BP神經網絡的輸入層節點數量、隱含層節點數量、輸出層節點數量，選擇Sigmoid函數作為各層節點間的傳遞函數[6]。設[Rij]表示輸入層和隱含層各神經元間彼此連接權值，[Rjk]表示隱含層和輸出層各神經元間彼此連接權值。

2） 隱含層輸出計算

隱含層輸出計算如式（1）所示：

3） 輸出層輸出計算

輸出層輸出計算如式（2）所示：

5） 目標函數結果判斷

算法終止條件為：誤差函數值滿足預設精度要求或學習次數超出限定值。如不滿足終止條件，則繼續選擇樣本輸入和樣本對應期望輸出，跳轉到步驟2），繼續訓練BP神經網絡直至誤差值達到標準或學習次數達到限定值[7]。

2? 基于粒子群算法的神經網絡優化

由于BP神經網絡存在收斂時間較長、容易陷入局部最優解等缺點，導致BP神經網絡音樂風格分類模型分類速率較慢，音樂風格分類結果不準確。為解決這一問題，利用收斂速度快、精度高的粒子群算法優化BP神經網絡的權值與閾值，確保權值與閾值的誤差最小，構建精準的神經網絡音樂分類模型。

2.1? 粒子群算法

粒子群優化（PSO）算法又稱為鳥群覓食算法，是一種進化計算技術，起源于鳥群捕食行為研究。受鳥類集群活動規律啟發，利用群體智能構建簡化模型[8]。PSO是一種基于迭代的優化算法，采用迭代方式從隨機解中搜尋最優解[9]。該方法的優勢在于精度高、收斂速度快、容易實現，無需調整大量參數[10]。PSO搜索空間上的粒子代表優化問題的候選解，每個粒子均存在一個適應度值和一個速度，適應度值由目標函數決定，速度決定粒子移動的方向和距離，依照最優粒子所處位置和粒子自身所在位置，粒子在搜索空間智能調節速度和適應度值，直至達到最終要求[11]。

粒子速度和位置在迭代中的更新方式見式（5）、式（6）：

式中：[?]，[ε]分別表示慣性權重和約束因子;[c1]，[c2]分別表示粒子跟蹤自己的權重系數、粒子跟蹤群體最優值權重系數;[γ]，[ψ]表示在[0，1]范圍內均勻分布的隨機數;[UkiH]，[Uk+iiH]表示更新前后粒子速度;[LkiH]，[Lk+iiH]表示更新前后粒子位置;[PkiH]，[PkgH]分別表示個體極值、全局極值。

2.2? 基于PSO的BP神經網絡優化

BP神經網絡在實際運用過程中容易出現收斂時間較長、陷入局部最優解等情況，為彌補該缺陷，采用PSO算法優化BP神經網絡權值和閾值[12]，具體實現步驟如下：

步驟1：還原PSO算法種群數量、粒子位置、粒子速度取值區間、學習因子、慣性權重以及最大迭代次數等參數。

步驟2：依照輸入、輸出信號數量構建BP神經網絡拓撲結構，初始化處理神經網絡權值和閾值長度[13]。

步驟3：編碼BP神經網絡的權值和閾值，獲取PSO算法初始種群。

步驟4：采用PSO優化BP神經網絡尋優迭代，獲取各組粒子的適應度值，通過適應度值明確粒子極值和粒子群極值，粒子歷史最佳位置為粒子尋優迭代過程中的最佳位置[14]。

步驟5：通過式（5）、式（6）更新處理迭代粒子的速度和位置。

步驟6：判斷結束條件。若適應度值符合預設精度或誤差要求、適應度值達到最大迭代次數，尋優迭代停止;此時粒子所在位置為所求目標的最優解，解碼最優解得到BP神經網絡的最優權值和閾值[15]。若不滿足結束條件，跳轉到步驟4。

基于PSO優化BP神經網絡流程如圖2所示。

基于PSO優化后的BP神經網絡權值和閾值構建BP神經網絡，輸入涵蓋音質、節奏、旋律特征的音樂樣本完成神經網絡訓練，構建基于PSO優化的神經網絡音樂風格分類模型，即基于群智優化神經網絡的音樂風格分類模型。

3? 音樂分類模型驗證

音樂風格分類模型訓練樣本包括六種音樂風格，共計300首音樂，基于該數據建立基于群智優化神經網絡的音樂風格分類模型。模型訓練結束后，選擇60首音樂作為測試樣本，展開音樂風格分類測試。

圖3? 最優個體適應度值趨勢

從圖3可以看出，粒子群算法優化后神經網絡迭代48次后收斂，收斂后曲線趨于平穩;而優化前神經網絡需迭代62次完成收斂，收斂之后產生短時期波動。由此可知，采用粒子群算法優化后神經網絡適應度值收斂速度較快、運行穩定。

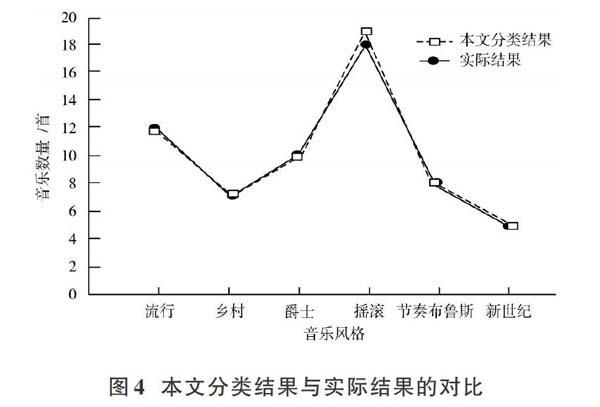
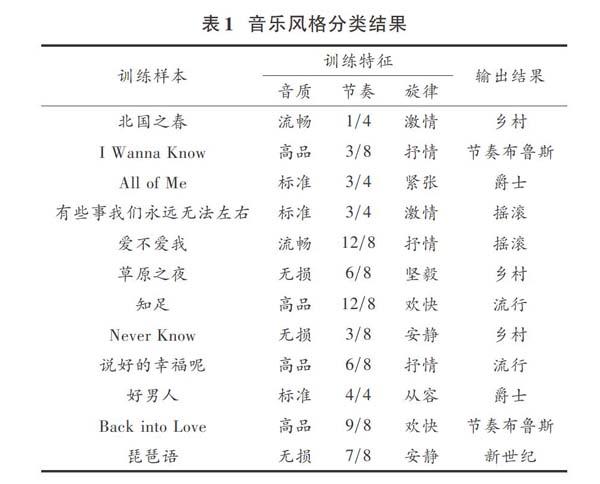
本文分類模型得到的音樂風格分類結果與實際結果對比情況如圖4所示，限于篇幅僅詳細列舉其中12首音樂分類結果與分類特征情況，如表1所示。

圖4中，本文模型大部分分類結果與實際分類結果一致，僅在搖滾音樂中錯誤識別一首音樂風格，由此可知，本文模型分類準確率高達98.3%，可靠性強。

音樂風格分類結果顯示，本文音樂模型分類結果不僅可以展示音樂風格，還能體現音樂的音質、節奏、旋律特征，為全面了解音樂風格提供有力的參考依據。

4? 結? 論

傳統神經網絡權值和閾值隨機性容易造成網絡訓練收斂時間長、陷于局部最優解，本文采用群智優化算法中的粒子群優化神經網絡的權值與閾值，解決了傳統神經網絡分類模型的缺陷，由此構建基于群智優化神經網絡分類模型，并將其應用于音樂風格分類。但受經驗水平等因素限制，本文模型中神經網絡泛化能力有待改善，今后的研究可充分結合其他高性能算法，改善神經網絡的泛化能力，進一步提高模型分類性能，達到更好的音樂風格分類效果。

參考文獻

[1] 胡昭華，余媛媛.深度卷積神經網絡在音樂風格識別中的應用[J].小型微型計算機系統，2018，39（9）：1932?1936.

[2] 郁偉生，鄧偉，張瑤，等.基于時間序列的音樂流行趨勢預測研究[J].計算機工程與科學，2018，40（9）：1703?1709.

[3] 邵曦，姚磊.基于SVM主動學習的音樂分類[J].計算機工程與應用，2016，52（6）：127?133.

[4] 陳月云，簡榮靈，趙庸旭.基于快速群體智能算法的毫米波天線設計[J].電子與信息學報，2018，40（2）：493?499.

[5] 張強，肖剛，藍屹群.基于BP神經網絡多類分類的湍流目標探測[J].系統工程與電子技術，2018，40（7）：75?79.

[6] 田靜，邢艷秋，姚松濤，等.基于元胞自動機和BP神經網絡算法的Landsat?TM遙感影像森林類型分類比較[J].林業科學，2017，53（2）：26?34.

[7] 曹兆偉，林寧，徐文斌，等.基于BP神經網絡的東嶼島遙感影像分類[J].海洋通報，2016，35（5）：587?593.

[8] 馬馳，趙亮，梅雪松，等.基于粒子群算法與BP網絡的機床主軸熱誤差建模[J].上海交通大學學報，2016，50（5）：686?695.

[9] 陳嘯，王紅英，孔丹丹，等.基于粒子群參數優化和BP神經網絡的顆粒飼料質量預測模型[J].農業工程學報，2016，32（14）：306?314.

[10] 王志芳，王書濤，王貴川.粒子群優化BP神經網絡在甲烷檢測中的應用[J].光子學報，2019，48（4）：141?148.

[11] 吳金文，王玉鵬，周海波.采用量子粒子群算法耦合差分進化算法優化BP神經網絡的銑床熱誤差預測研究[J]. 制造技術與機床，2018（6）：114?118.

[12] 游丹丹，陳福集.基于改進粒子群和BP神經網絡的網絡輿情預測研究[J].情報雜志，2016，35（8）：156?161.

[13] 張璐，雷雪梅.基于粒子群優化BP神經網絡的養腸胃菜譜判定[J].計算機科學，2016，43（z2）：63?66.

[14] 劉加存，梅其祥，楊東紅.基于盲動粒子群頻率分解的極速學習機神經網絡建模[J].信息與控制，2017，46（1）：60?64.

[15] 林宇鋒，鄧洪敏，史興宇.基于新的改進粒子群算法的BP神經網絡在擬合非線性函數中的應用[J].計算機科學，2017，44（11A）：51?54.