四輪獨立驅(qū)動FSEC 賽車穩(wěn)定性控制*

宋成鏢 李剛

（遼寧工業(yè)大學(xué)）

隨著汽車技術(shù)的不斷進(jìn)步，關(guān)于車輛穩(wěn)定性控制的研究也十分豐富[1]。在控制方法方面已經(jīng)從最初的差動制動擴展到主動前輪轉(zhuǎn)向控制、四輪轉(zhuǎn)向控制、直接橫擺力矩控制等[2]。應(yīng)用控制理論從PID 控制、最優(yōu)控制擴展到自適應(yīng)控制、模糊邏輯控制以及人工神經(jīng)網(wǎng)絡(luò)控制等[3-5]。由于大學(xué)生電動方程式賽車是近幾年興起的[6]，對其穩(wěn)定性控制方面的研究較少，但是由于其在安全性方面的重要作用，已逐漸被重視。為充分利用四輪獨立驅(qū)動FSEC 賽車四輪力矩獨立可控的優(yōu)勢，文章選取直接橫擺力矩控制方式對賽車進(jìn)行穩(wěn)定性控制，配合目前最成熟，應(yīng)用最為廣泛的PID 算法，能夠最大程度地保證控制算法的實時性，提升控制效果。

1 直接橫擺力矩控制器搭建

直接橫擺力矩控制器結(jié)構(gòu)，如圖1 所示。采用分層式結(jié)構(gòu)，包括信號采集層、決策計算層、控制分配層和執(zhí)行機構(gòu)層。在信號采集層，模擬駕駛員操縱命令，通過PID 控制車輛的總驅(qū)動力矩，控制車速變化；決策計算層通過車速和駕駛員的轉(zhuǎn)向盤轉(zhuǎn)角輸入，計算出目標(biāo)橫擺角速度，并與實際橫擺角速度值做差，輸入PID控制器，給出附加橫擺力矩；控制分配層根據(jù)來自信號采集層的總目標(biāo)驅(qū)動力和所需的附加橫擺力矩，通過差動驅(qū)動規(guī)則對四輪驅(qū)動力進(jìn)行分配；輸出的4 個車輪的驅(qū)動力，通過執(zhí)行機構(gòu)層的四輪輪轂電機實現(xiàn)穩(wěn)定性控制。

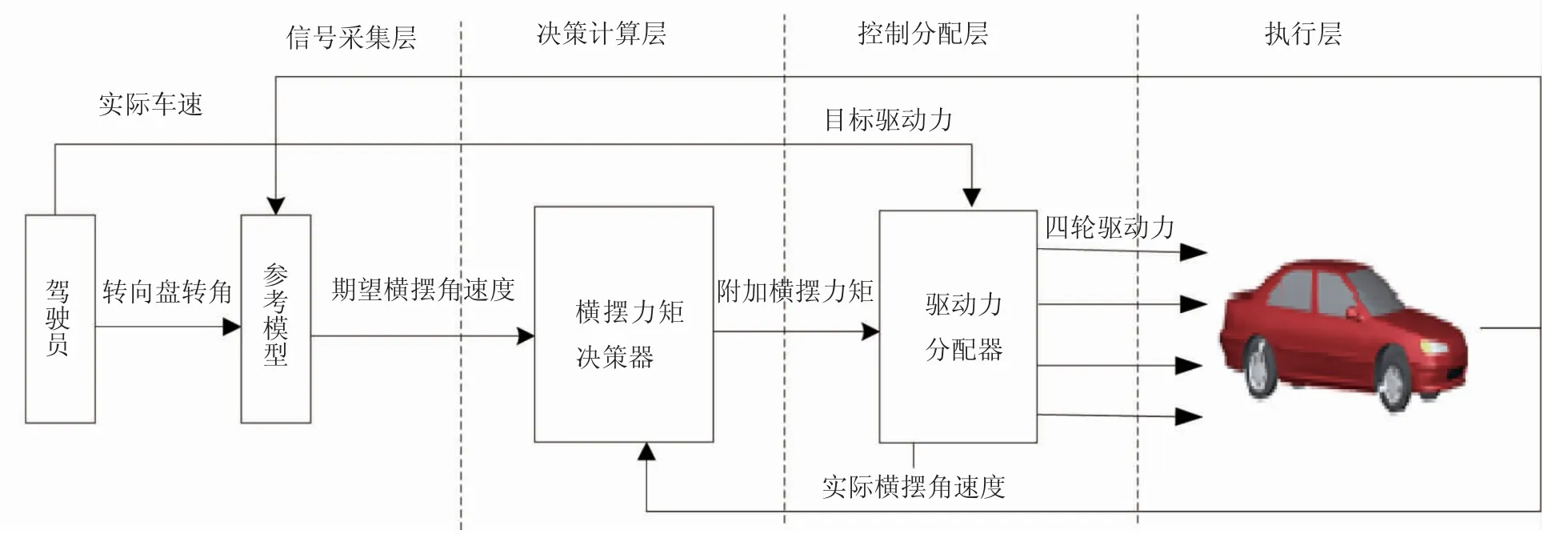
圖1 橫擺力矩控制原理圖[7-8]

1.1 參考模型

線性二自由度車輛動力學(xué)模型能夠很好地反映車輛的穩(wěn)定性參數(shù)狀態(tài)，并且在運算簡便性與實時性方面具有一定優(yōu)勢[9-10]，因此被眾多車輛操縱穩(wěn)定性研究選為理想模型，如圖2 所示。

圖2 線性二自由度模型

根據(jù)模型可以看出，車輛穩(wěn)定性問題可由車輛側(cè)向運動與橫擺運動表征，其微分方程為：

式中：M——汽車總質(zhì)量，kg；

V——速度，m/s；

I——車輛繞Z軸的轉(zhuǎn)動慣量，kg·m2；

Fyf——前輪的側(cè)向力，N；

Fyr——后輪的側(cè)向力，N；

β——質(zhì)心側(cè)偏角，rad；

γ——橫擺角速度，rad/s；

a，b——重心與前、后軸之間的距離，m；

βf，βr——前、后輪胎側(cè)偏角，rad。

設(shè)前后輪的側(cè)偏剛度分別為Kf和Kr，并設(shè)Fyf和Fyr分別與前后輪的側(cè)偏角βf和βr成正比，即輪胎在線性區(qū)工作，那么輪胎側(cè)向力，如式（2）所示。

將式（2）代入式（1）中，并設(shè)前輪轉(zhuǎn)角為 δf，另外在穩(wěn)態(tài)轉(zhuǎn)向條件下，車輛質(zhì)心側(cè)偏角β、橫擺角速度γ 均不變，即可得：

通過式（3）可知，表征車輛穩(wěn)定性的參數(shù)是關(guān)于β，γ，δf，V的方程組，其中速度V與前輪轉(zhuǎn)角 δf都由駕駛員控制輸入，而質(zhì)心側(cè)偏角β 在實際車輛控制中獲取較困難，因此最后選取橫擺角速度表征車輛的穩(wěn)定狀態(tài)，關(guān)系為：

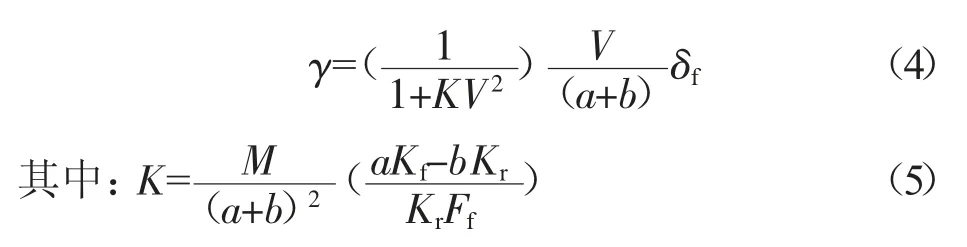
式中：K——穩(wěn)定性因數(shù)，s2/m2。

1.2 橫擺力矩決策控制器

通過上述對參考模型的分析可知，車輛的穩(wěn)定性控制問題可用質(zhì)心側(cè)偏角與橫擺角速度表征，但是實際車輛控制中質(zhì)心側(cè)偏角獲取比較困難。另外，質(zhì)心側(cè)偏角不超過一定范圍時，橫擺角速度完全能夠反映車輛的穩(wěn)定性狀態(tài)。因此文章選取橫擺角速度為控制目標(biāo)量。控制原理，如圖3 所示。

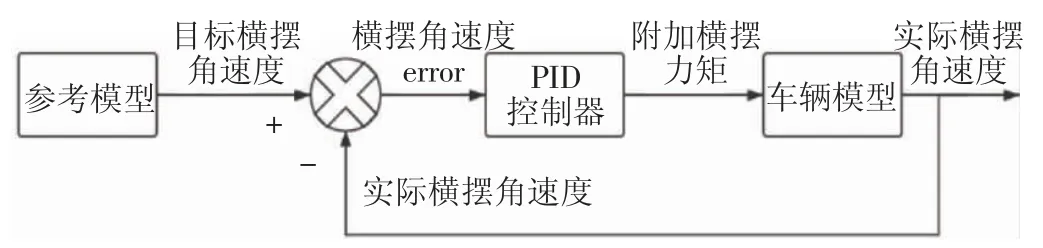
圖3 橫擺力矩決策算法原理圖

定義實際與理想橫擺角速度偏差為：

所需附加橫擺力矩為：

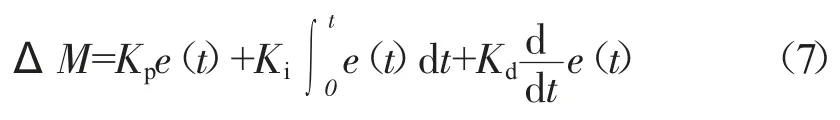
式中：e（t）——橫擺角速度偏差，rad/s；

γ*——目標(biāo)橫擺角速度，rad/s；

γ——實際橫擺角速度，rad/s；

ΔM——附加橫擺力矩，N·m；

Kp，Ki，Kd——比例系數(shù)、積分系數(shù)、微分系數(shù)。

1.3 驅(qū)動力分配器

4 個車輪驅(qū)動力矩可通過各輪驅(qū)動電機的轉(zhuǎn)矩?fù)Q算得到：

式中：Fxi——某車輪驅(qū)動力，N；

Txi——某輪驅(qū)動力矩，N·m；

R——車輪滾動半徑，m。

當(dāng)車輛直線行駛時，四輪驅(qū)動力相等。當(dāng)車輛轉(zhuǎn)彎時，根據(jù)決策出的附加橫擺力矩符號對車輛狀態(tài)進(jìn)行判斷：當(dāng)附加橫擺力矩大于0 時，認(rèn)為車輛需要逆時針的附加橫擺力矩，此時應(yīng)適當(dāng)增大右側(cè)車輪驅(qū)動力，減小左側(cè)車輪驅(qū)動力；當(dāng)附加橫擺力矩小于0 時，認(rèn)為車輛需要順時針的附加橫擺力矩，此時應(yīng)適當(dāng)增大左側(cè)車輪驅(qū)動力，減小右側(cè)車輪驅(qū)動力，具體的分配規(guī)則為：

當(dāng) ΔM=0 時：

當(dāng) ΔM＞0 時：

當(dāng) ΔM＜0 時：

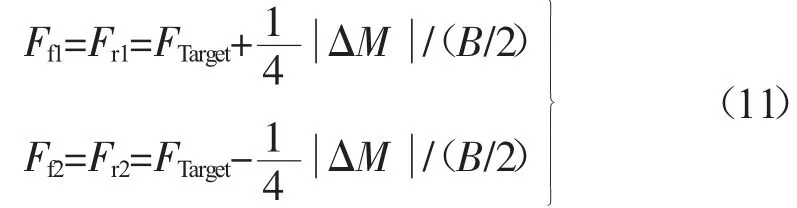
式中：Ff1，F(xiàn)f2，F(xiàn)r1，F(xiàn)r2——汽車左前輪、右前輪、左后輪、右后輪的驅(qū)動力，N；

B——輪距，m；

FTarget——油門請求驅(qū)動力，N。

2 仿真試驗驗證

2.1 CarSim 車輛模型建立

基于車輛動力學(xué)仿真軟件CarSim 中的方程式賽車模型進(jìn)行仿真試驗，更新賽車參數(shù)并將傳動系統(tǒng)與發(fā)動機系統(tǒng)用Simulink 模型代替，主要參數(shù)如表1 所示。

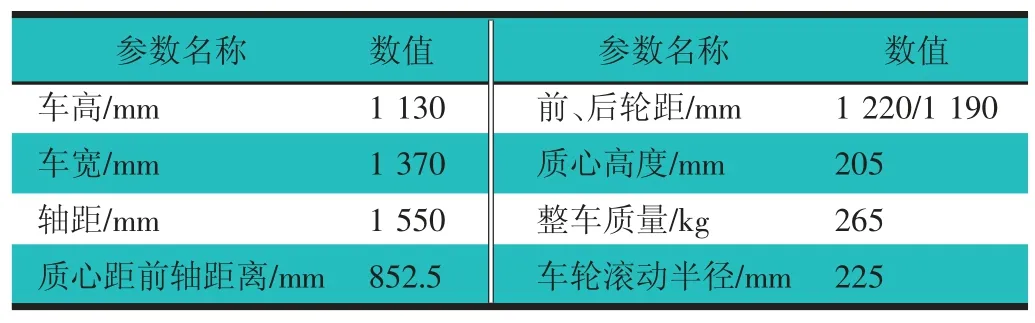
表1 基于CarSim 軟件進(jìn)行仿真試驗的賽車參數(shù)情況

2.2 仿真試驗

CarSim 與Simulink 聯(lián)合仿真試驗選取2 個典型的試驗場景，分別是快速移線仿真試驗與蛇形保持仿真試驗。

2.2.1 快速移線仿真試驗

車輛速度為70 km/h、高附著系數(shù)路面、閉環(huán)雙移線轉(zhuǎn)向控制，在70 m 時實施變道動作，向左移動3.5 m，隨后變更回原來車道。試驗結(jié)果，如圖4 和圖5 所示。

圖4 快速移線仿真試驗橫擺角速度曲線

圖5 快速移線仿真試驗驅(qū)動力矩曲線

從橫擺角速度仿真結(jié)果中可以看出，施加控制車輛可以較好地跟蹤目標(biāo)橫擺角速度。從驅(qū)動力分配曲線可以看出，施加控制后車輛的左右側(cè)車輪轉(zhuǎn)矩差異明顯，控制效果顯著。

2.2.2 正弦保持仿真試驗

車輛初始速度為80 km/h、高附著路面、閉環(huán)正弦轉(zhuǎn)向輸入，幅值1.5 m，每隔30 m 設(shè)置1 個樁桶作為參考標(biāo)識。試驗結(jié)果，如圖6 和圖7 所示。

圖6 正弦保持仿真試驗橫擺角速度曲線

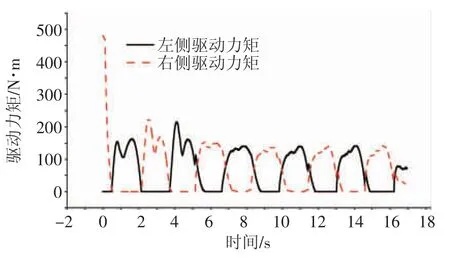
圖7 正弦保持仿真試驗驅(qū)動力矩曲線

從橫擺角速度仿真結(jié)果可以看出，在頻繁的轉(zhuǎn)向輸入下車輛已經(jīng)不能很好地跟蹤目標(biāo)橫擺角速度，但是相對于無控制車輛，施加控制的車輛依然能夠在響應(yīng)速度與跟蹤幅度上占有一定優(yōu)勢。從驅(qū)動力分配曲線圖可以看出，施加控制后，車輛的左右側(cè)車輪轉(zhuǎn)矩變化十分均勻，控制效果穩(wěn)定。

3 結(jié)論

文章利用四輪驅(qū)動電動方程式賽車驅(qū)動力矩獨立可控的優(yōu)勢，基于PID 控制理論設(shè)計直接橫擺力矩穩(wěn)定性控制算法，對驅(qū)動力進(jìn)行合理分配，能夠有效提升車輛操縱穩(wěn)定性。選取雙移線與正弦保持試驗工況對算法進(jìn)行仿真試驗，結(jié)果表明施加控制的車輛能夠較好地跟蹤目標(biāo)橫擺角速度，實現(xiàn)車輛的良好控制。文章提出算法是建立在參考模型線性區(qū)間的，下一階段應(yīng)將非線性因素加入進(jìn)來，建立更加完善的穩(wěn)定性控制算法。