地鐵扣件軌下調高對T型螺栓的影響分析

胡宏力 韋凱 王紹華 謝夢 周華龍

（1.西南交通大學高速鐵路線路工程教育部重點實驗室，成都 610031；2.中鐵二院工程集團有限責任公司，成都 610031）

隨著我國城市化進程的快速推進，軌道交通已經成為緩解城市交通擁堵的有效方案。扣件系統是軌道結構的關鍵部件，主要功能包括固定鋼軌正確位置及對鋼軌進行高低調整。調高扣件在路基沉降等地段得到了廣泛使用。

T型螺栓是有螺栓扣件系統中的關鍵零部件，一旦失效，會導致彈條扣壓鋼軌的功能無法實現，直接影響軌道結構的整體穩定，甚至危及行車安全［1］。鐵路扣件中的T型螺栓除了受鐵墊板等零部件的約束作用，還受列車振動荷載的影響，其受力有別于傳統的機械領域，所以相關研究成果不能簡單套用［2］。目前關于調高扣件的研究較少，關于鐵路扣件關鍵零部件的研究也主要聚焦在彈條上。因此研究扣件調高對T型螺栓受力的影響有著重要的理論意義和實用價值。

一地鐵路段在鋼軌高低調整時采用在軌下墊板下加墊調高墊板的方法。加墊軌下調高墊板有可能使彈條發生轉動，改變扣件的安裝情況，進而對扣件系統中緊固彈條的T型螺栓產生影響。本文對Ⅱ型彈條扣件系統關鍵零部件建立有限元模型，模擬鋼軌作用在扣件系統上的位移，得到彈條對平墊圈的動態荷載，計算T型螺栓在不同軌下調高量下的最大等效應力，分析扣件軌下調高對T型螺栓受力的影響。

1 有限元建模

1.1 計算模型

扣件系統中的T型螺栓除了受螺栓預緊力F（本文不考慮螺栓預緊力的偏心）和鐵墊板的約束力N外，還要承受彈條的動態荷載P［3］，如圖1所示。

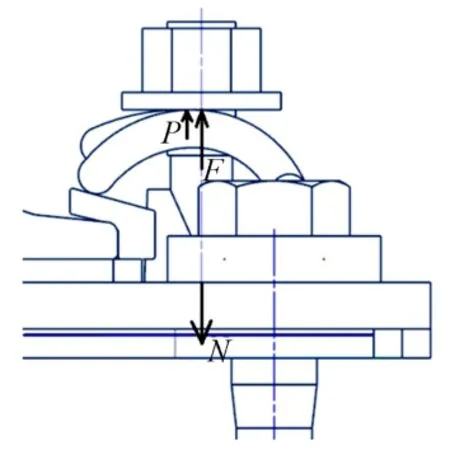
圖1 T型螺栓受力示意

為減小計算量，本文采用單個T型螺栓進行計算（圖2（a）），通過在螺栓頂部施加作用荷載模擬T型螺栓與平墊圈及螺母之間的約束，其中彈條對平墊圈的動態荷載P通過建立彈條系統模型（圖2（b））仿真計算得到。

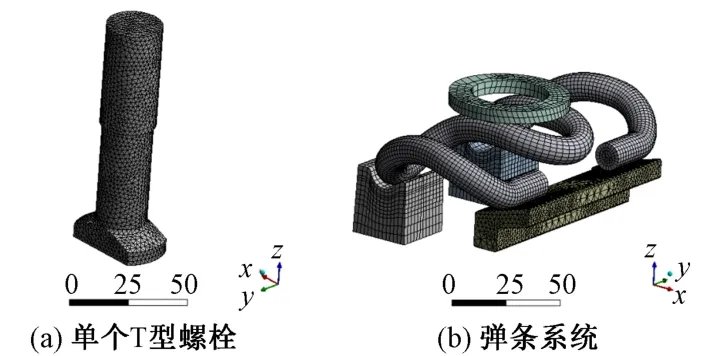
圖2 有限元模型（單位：mm）

1.2 材料屬性和本構關系

Ⅱ型彈條的材料為60Si2CrA［4］，T型螺栓材料為Q235A型鋼［5］，均屬于彈塑性材料。為保證計算合理性，對彈條和T型螺栓均采用理想線性強化彈塑性模型，強化模量E1=0.1E，E為彈性模量。本構關系如圖3所示。應力應變曲線OAB中的A點為屈服點，即當應變為εs時，材料剛達到屈服狀態，對應的應力為σs。

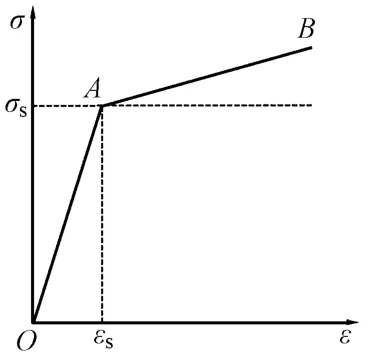
圖3 理想線性強化彈塑性模型

扣件系統各部件材料參數見表1。

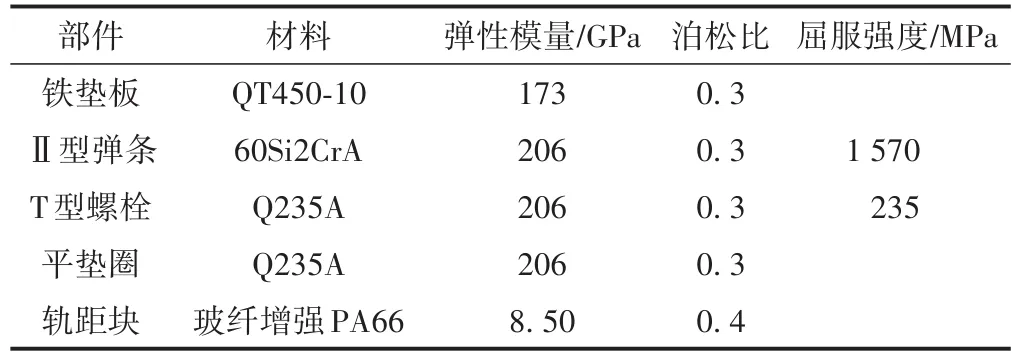
表1 扣件系統各部件材料參數

1.3 接觸關系與邊界條件設置

將彈條與其有接觸的部件之間均設置為摩擦接觸，以保證足夠的接觸面［6］。接觸算法設置為擴展拉格朗日算法。各接觸對之間的摩擦及運動狀態按照庫侖摩擦模型確定［7］，具體設置見表2。

表2 接觸關系

本文不考慮鐵墊板的受力對彈條的影響，模型中將鐵墊板凹槽底面設為固定約束，對T型螺栓T腳處4個方向分別施加法向位移約束來模擬其與鐵墊板的接觸。

1.4 驗證模型的正確性

參照文獻［8］的方法，通過彈條彈程與扣壓力的關系對模型進行驗證，結果見圖4。可知，彈程為10 mm時，扣壓力為10.67 kN，符合規范中彈條的正常安裝要求，即扣壓力不小于10 kN，彈程為10 mm［9］。因此該模型可用于計算分析。

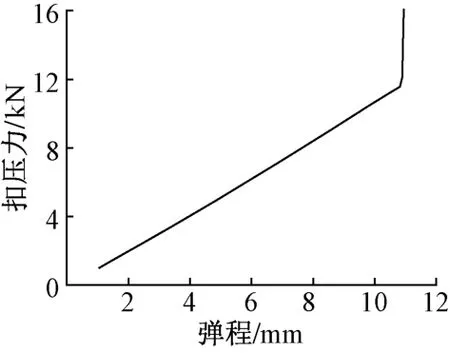
圖4 彈程與扣壓力的關系

1.5 計算工況

螺栓預緊力F與螺母擰緊力矩T的關系式為［10］：

式中：K為擰緊力矩系數；d為螺栓公稱直徑，mm。

T在一般地段（包括直線地段及半徑不小于600 m的曲線地段）取100～120 N?m，在半徑小于600 m的曲線地段（以下簡稱小半徑曲線地段）取140～170 N?m；K=0.2；d=24 mm。代入式（1），可得F在一般地段和小半徑曲線地段分別為20.833～25.000 kN和29.167～35.417 kN。

模型中，通過在軌距塊底部施加垂向位移來模擬從鋼軌傳來的動態荷載。根據文獻［11］現場實測結果，鋼軌經絕緣塊傳遞給彈條的垂向位移振幅v為0.5，-2.0 mm。從計算結果中分別提取在不同螺栓預緊力下v為0（無位移），0.5，-2.0 mm時彈條與平墊圈之間的作用力Q0，Q1，Q2。v為 0.5，-2.0 mm時，彈條對平墊圈的動態荷載P分別為Q1－Q0，Q2－Q0。計算可得，P的變化范圍為-2.801～0.453 kN。其中，正值表示彈條處于加載階段，對螺栓的作用力增大；負值表示彈條處于卸載階段，對螺栓的作用力減小。

根據扣件的實際安裝狀況，經平墊圈傳遞至T型螺栓的P往往表現為偏心，設偏心距為e。將P的作用點移至螺栓中心軸位置會產生一個等效力矩M，滿足M=P e。根據力的平衡，鐵墊板對T型螺栓的約束力N=P+F。彈條處于加載階段時，取P的最大正值0.453 kN，則N的最大值在一般地段和小半徑曲線地段分別為21.286～25.453 kN和29.62～35.87 kN；彈條處于卸載階段時，取P的最大負值-2.801 kN，則N的最大值在一般地段和小半徑曲線地段分別為18.032～22.199 kN和26.366～32.616 kN。

在三維模型中可模擬軌下墊板調高行為。考慮到軌下調高墊板的配置規格，忽略T型螺栓桿長的限制，設計了7種不同的軌下調高量，分別為0（未調高），5，10，15，20，25，30 mm。在不同調高量下，荷載P的偏心距不同，由此產生的等效力矩M也不同，計算結果見表3。其中，正值、負值分別對應彈條的加載、卸載階段。

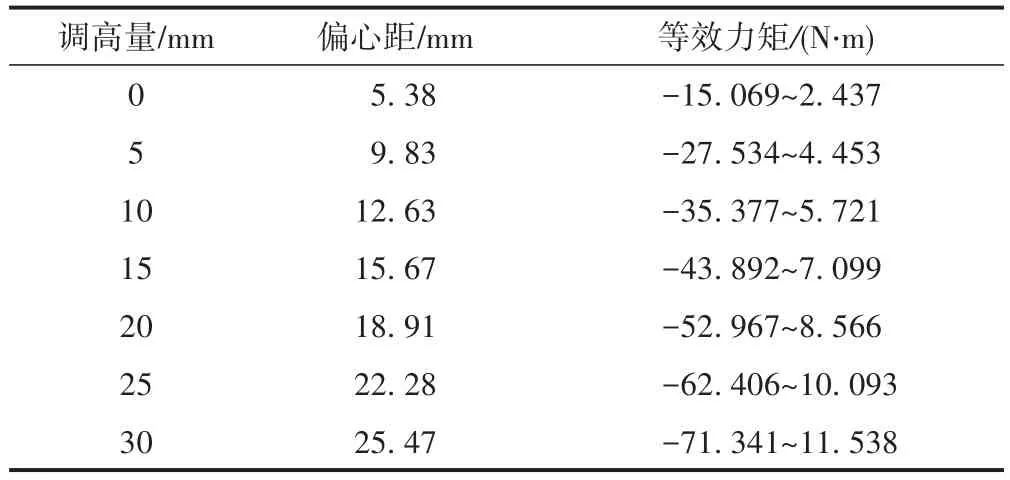
表3 不同調高量對應的等效力矩

考慮最不利情況，將不同地段條件下T型螺栓在不同階段受到的最大等效軸向約束力的最大、最小值分別與不同調高量對應的等效力矩的最大、最小值進行組合，得到最不利計算工況組合。在加載和卸載階段均有28種最不利計算工況，見表4。

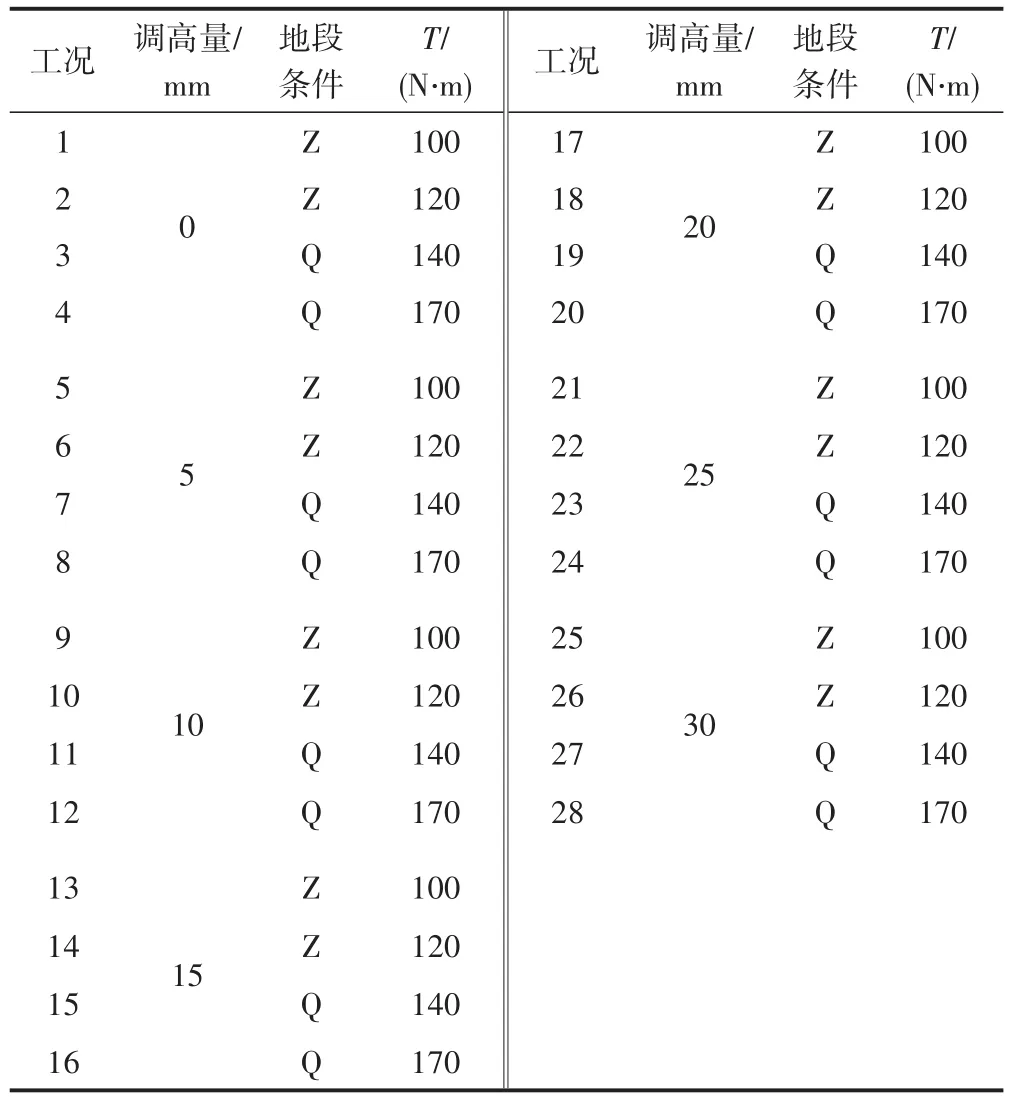
表4 最不利計算工況

2 求解結果分析

對比加載和卸載2個階段各工況的計算結果，發現彈條處于加載階段時螺栓的受力更為不利。以加載階段時的工況16和工況26為例，T型螺栓的等效應力云圖見圖5。可知，工況16和工況26中T型螺栓的最大等效應力均出現在螺栓根部位置，分別為234.34，228.87 MPa。工況16的最大等效應力剛好接近屈服強度（235 MPa），說明在小半徑曲線地段，當加墊的軌下調高墊板的厚度為15 mm時，T型螺栓在可能出現的最大螺母擰緊力矩作用下也恰好在安全范圍內。工況26中T型螺栓尚未達到屈服強度，說明在一般地段，當加墊的軌下調高墊板的厚度為30 mm時，T型螺栓在正常范圍內的螺母擰緊力矩作用下不會發生屈服現象，仍能滿足使用要求。

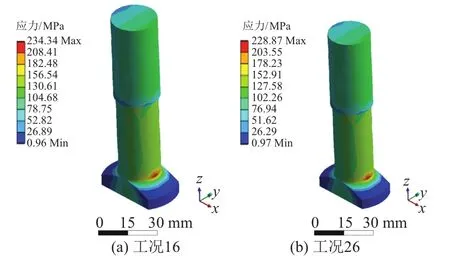
圖5 T型螺栓的等效應力云圖

0 15

研究不同擰緊力矩下T型螺栓的等效應力云圖，發現其最大等效應力均出現在螺栓根部位置，其值見圖6。

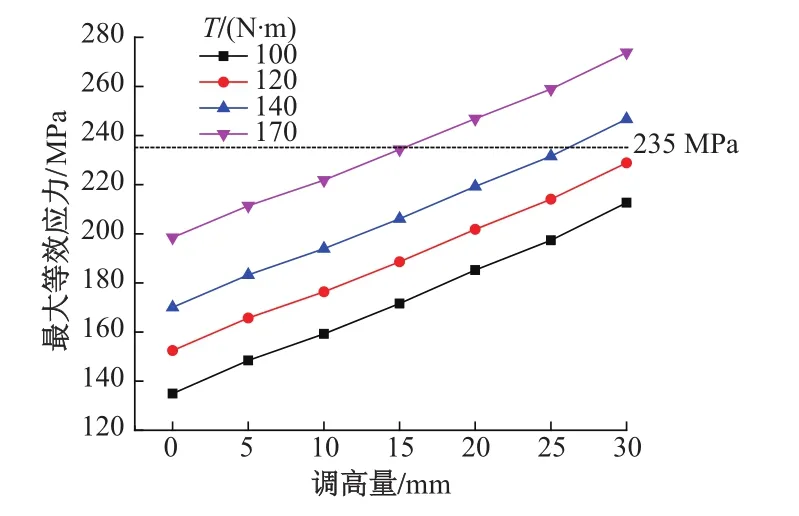
圖6 不同擰緊力矩下T型螺栓的最大等效應力值

由圖6可知，螺母擰緊力矩和軌下調高量不同時，扣件中T型螺栓的最大等效應力不同。螺母擰緊力矩相同時，隨著軌下調高量的增加，T型螺栓最大等效應力顯著增加；軌下調高量相同時，螺母擰緊力矩越大，T型螺栓最大等效應力越大。

為保證T型螺栓能正常工作（不發生屈服），在小半徑曲線地段扣件軌下調高允許值為15 mm。而對于一般地段，允許加墊厚度為30 mm的軌下調高墊板，但根據曲線趨勢預測，若繼續增大軌下調高量則T型螺栓將無法滿足使用要求。

3 結論

為了研究地鐵扣件軌下調高對T型螺栓受力的影響，本文建立了Ⅱ型彈條扣件系統關鍵零部件的三維實體有限元模型，通過改變施加在螺栓頂部的外力荷載來模擬不同地段螺栓預緊力的大小和調高前后彈條對螺栓平墊圈動態荷載的偏心程度，計算T型螺栓在不同螺母擰緊力矩和軌下調高量下的最大等效應力。得出結論如下：

1）無論是在一般地段還是半徑小于600 m的曲線地段，在軌下加墊調高墊板后T型螺栓的受力情況會惡化；相比一般地段，半徑小于600 m的曲線地段調高前后的最大應力值均較大，說明小半徑曲線地段T型螺栓的受力情況更不利，在極端條件下更容易屈服或疲勞斷裂。

2）在動態荷載作用下，T型螺栓主要受螺母擰緊力矩和軌下調高量的影響。螺母擰緊力矩相同時，隨著軌下調高量的增加，T型螺栓根部最大等效應力顯著增加；軌下調高量相同時，螺母擰緊力矩越大，則T型螺栓根部最大等效應力越大。

3）扣件系統中T型螺栓為剛性部件，應盡量避免其在服役過程中出現塑性變形，且需保證一定彈性安全余量。在正常螺母擰緊力矩條件下，建議在半徑小于600 m的曲線地段軌下最大調高量不超過15 mm，一般地段不超過30 mm。