Ca5Zn3相穩定性和物理性質的第一性原理研究*

溫姜霞，吳升聰，王 俊，陶小馬，陳紅梅，歐陽義芳

( 廣西大學物理科學與工程技術學院，廣西南寧 530004)

0 引言

近年來，針對具有A5B3型化合物的研究越來越多，這是因為該類化合物具有獨特的物理化學性能[1-5]，研究表明超過40個金屬間化合物具有A5B3型結構。常見的結構類型有Cr5B3型、W5Si3型和Mn5Si3型這3類，Tao等[5-8]利用基于密度泛函的第一性原理方法對Ta5Si3、W5Si3、V5Si3以及Tl5Te3等化合物的物理化學性能進行模擬計算研究，獲得了這些化合物的結構穩定性、力學性能、電子結構特性以及熱物理性能和熱電性能等。含堿土金屬Ca的化合物中，Ca5Si3因其有潛在的儲氫性能[3]和熱電性能[9]備受關注。然而在含Ca的化合物中，Ca5Zn3也具有Cr5B3型結構[1]。2012年，Yang等[10]利用基于密度泛函的第一性原理的方法對Ca-Zn體系的7個化合物進行了計算研究，計算獲得了形成焓、彈性常數和電子態密度等信息。然而，至今還沒有針對Ca5Zn3的更加系統研究的報道。為了能夠獲得更加系統的物理性能，本文將利用基于密度泛函的第一性原理方法對Ca5Zn3化合物進行系統計算研究，獲得該化合物的熱力學穩定性、力學性能、電子結構特性，并結合德拜模型對其熱物理性能進行研究和預測。

1 材料與方法

1.1 Ca5Zn3的晶體結構

采用Cr5B3型、W5Si3型和Mn5Si3型等3種結構來討論Ca5Zn3結構穩定性。其中Cr5B3型結構是一個四方晶系的結構，Pearson符號為tI32，共有4種不同占位，Cr占據16l和4c位，B占據4a和8h位。每個Cr5B3型結構單胞中含有10個Cr原子，6個B原子。其余兩種結構的具體信息可參見文獻[5]。3種晶體結構如圖1所示。

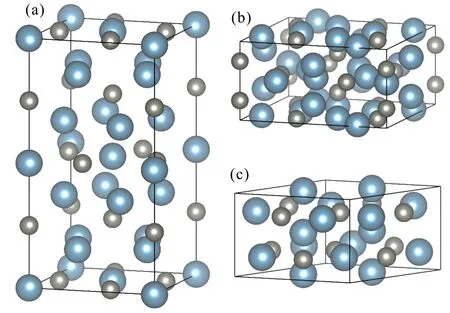
(a) Cr5B3型，(b) W5Si3型，(c) Mn5Si3型;藍色為Ca原子，灰色為Zn原子(a) Cr5B3 prototype，(b) W5Si3 prototype，(c) Mn5Si3 prototype;the blue atom is Ca，the grey atom is Zn圖1 Ca5Zn3化合物的3種晶體結構Fig.1 Tree crystal structures of Ca5Zn3 compounds

1.2 計算方法

本文采用基于密度泛函理論(Density Functional Theory，DFT)的第一性原理計算軟件包Vienna Ab initio Simulation Package (VASP)[11]進行計算。第一性原理計算方法是投影綴加波方法[12-13]，交換關聯勢采用廣義梯度近似的Perdew-Burke-Ernzerhof (PBE)方案[14]。布里淵區積分采用Monkhorst Pack布點方法[15]，對于Cr5B3和W5Si3結構，K點取11×11×11，而對Mn5Si3結構，K點為9×9×11。在本文計算中,波函數的截斷能設置為500 eV，能量收斂精度為10-6eV。在進行性能計算前，所有結構都進行全優化，直到原子間的力小于0.01 eV/?為止，以保證計算的準確性。有關形成焓、彈性常數以及熱物理性質的計算方法參見文獻[5]。

Ca5Zn3化合物形成焓可以用以下的公式進行計算：

ΔH(Ca5Zn3)=Etotal(Ca5Zn3)-5Etotal(Ca)-3Etotal(Zn)，

(1)

其中，Etotal(Ca5Zn3)、Etotal(Ca)和Etotal(Zn)分別是Ca5Zn3合金、Ca以及Zn元素的總能量。

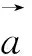
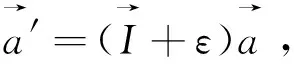
(2)

(3)

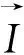
(4)

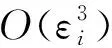
Cr5B3結構類型的Ca5Zn3是四方晶系。四方晶系有6個獨立彈性常數，分別為C11,C12,C13,C33,C44和C66。通過下面6個形變矩陣可以求得相應彈性常數(表1)。

表1 四方晶系形變矩陣及相應形變能Table 1 Deformation matrix of the tetragonal system and the corresponding deformation energy

德拜溫度作為一個基本的物理參數，與熱容、彈性常數等有著密切聯系。一般來說，德拜溫度越高，化合物熔點越高，意味著原子間的相互作用越強。一般來說，德拜溫度(Θ)可以從平均聲速(um)進行估算:

(5)

其中,h和kB分別是普朗克常數和玻爾茲曼常數，V是原子平均體積，在多晶體中的平均聲速(um)可以用以下公式計算:

(6)

其中，ut和ul分別是橫向聲速和縱向聲速，這兩種聲速可以通過以下公式獲得:

(7)

(8)

其中,G為剪切模量，B為體積模量，ρ為質量密度。

2 結果與分析

2.1 結構穩定性能

為了獲得Ca5Zn3的結構穩定性，考慮了Cr5B3型、W5Si3型和Mn5Si3型3種晶體結構，計算獲得的晶格常數、形成焓(表2)，同時分析3種晶體結構的總能隨體積變化的關系(圖2)。本文計算獲得的Cr5B3型晶格常數為7.865 6 ?和15.366 3 ?，Bottcher等[1]的實驗值為 7.963 ?和15.407 ?，其他第一性原理計算值[10]為 7.802 ?和15.620 ?。本文的晶格常數計算值與實驗值之間的誤差為1.22%和0.26%，比Yang等[10]計算值的誤差(2.02%，1.38%)小，說明本文計算獲得的晶格常數更為合理。W5Si3型和Mn5Si3型Ca5Zn3化合物的晶格常數也作為預測結果列于表2。從表2中給出的形成焓可以看出，Cr5B3型Ca5Zn3的形成焓最低為-0.201 eV/atom，其他兩種晶體結構的形成焓分為-0.160 eV/atom和-0.164 eV/atom。從能量的角度，其他兩種晶體結構的形成焓比Cr5B3型的形成焓高出0.04 eV/atom，因此，具有Cr5B3結構的Ca5Zn3是最穩定的化合物。從圖2中可以看出，具有Cr5B3型的Ca5Zn3具有最低的總能量，同樣表明Cr5B3型Ca5Zn3是最穩定的化合物，這與Bottcher等[1]的實驗結果是一致的。

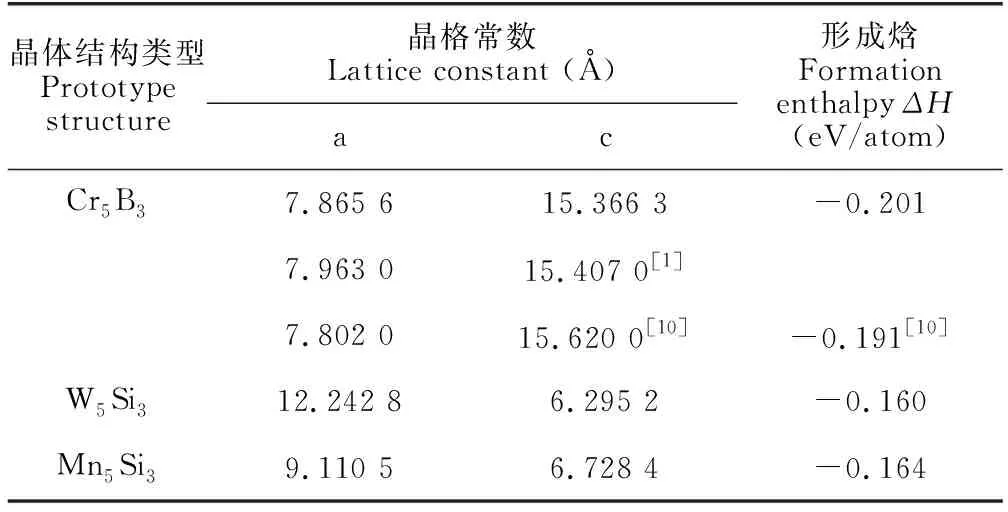
表2 Ca5Zn3化合物的晶格常數和形成焓Table 2 Lattice constant and formation enthalpy of the Ca5Zn3 compounds

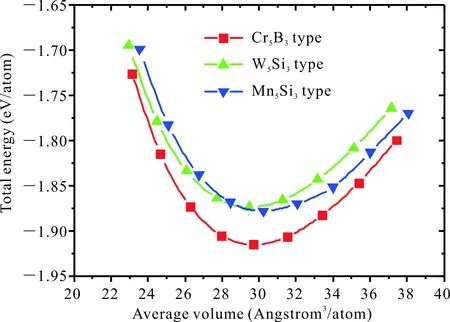
圖2 具有3種不同晶體結構的Ca5Zn3化合物總能量與體積的關系Fig.2 Relationship of total energy and volume of Ca5Zn3 compounds with three different crystal structures

2.2 力學性能

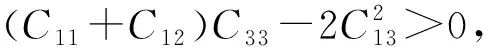
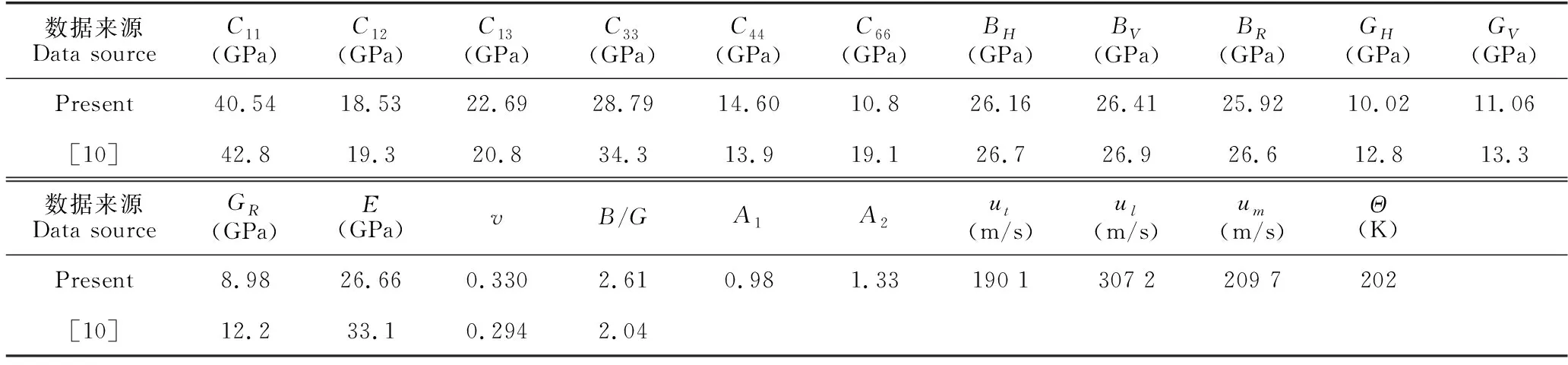
表3 Ca5Zn3化合物的力學性能參數Table 3 Mechanical property parameters of Ca5Zn3 compounds

B/G值一般用來預測化合物的脆韌性[17]，該比值大于1.75，化合物呈現韌性，比值越大韌性越大；反之，該比值小于1.75，則化合物呈現脆性，且比值越小脆性越大。Ca5Zn3的B/G值為2.61，說明該化合物呈現韌性。為了研究化合物的各向異性，對于四方晶系來說，一般用A1=2C66/(C11-C12)和A2=2C44/(C11-C12)進行說明。該數值為1時，則呈現各向同性，偏離1越遠則各向異性越明顯。為了更加明顯地呈現該化合物的各向異性，圖3給出了楊氏模量的空間分布圖，由此可以清晰地看出在不同的方向上，楊氏模量的數值存在明顯的差異。

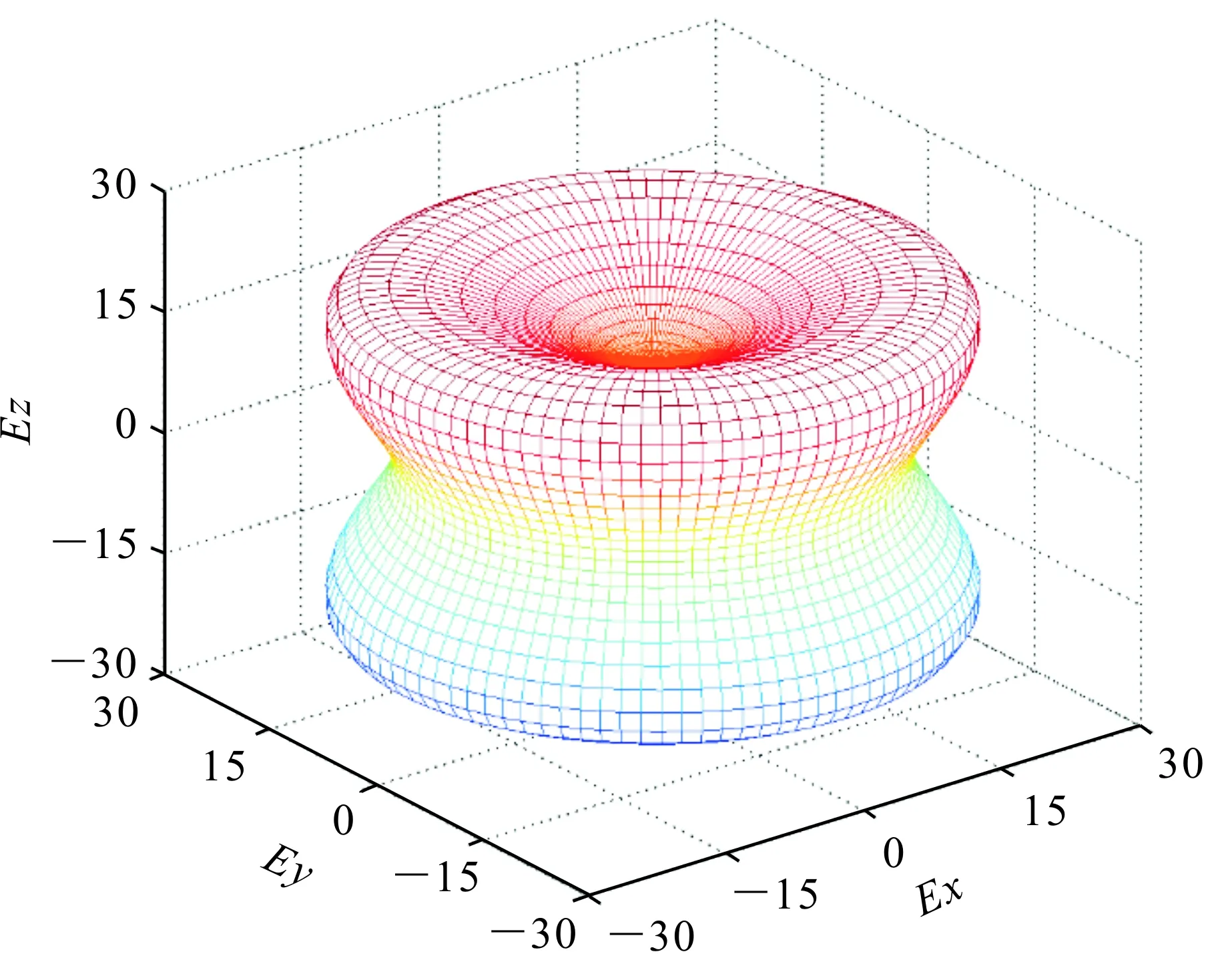
圖3 Ca5Zn3化合物楊氏模量的空間分布(GPa)Fig.3 Spatial distribution of Young's modulus for Ca5Zn3 compounds (GPa)

2.3 電子結構特性

為了深入了解該化合物原子間的相互作用，本文計算了該化合物的電子態密度和電荷密度差(圖4)。由圖4a可以看出，在費米面以下的電子態密度，主要是Ca的s電子和p電子以及Zn的s電子和p電子的貢獻，費米面以上的電子態密度主要是Ca的d電子和Zn的p電子的貢獻。在費米面附近，Ca的p電子和d電子跟Zn的p電子發生雜化效應。在費米能外態密度不為零，說明該化合物呈現金屬性。由圖4b和圖4c可知，Ca和Zn之間主要呈現離子鍵特性，Ca失去電子，而Zn則獲得電子，這個和圖4a中的電子態密度在費米面附近發生雜化效應是一致的。由于Ca的電負性為1.0，Zn的電負性為1.6，電負性越大表明越容易獲得電子，由此可見本文的計算結果是合理的。

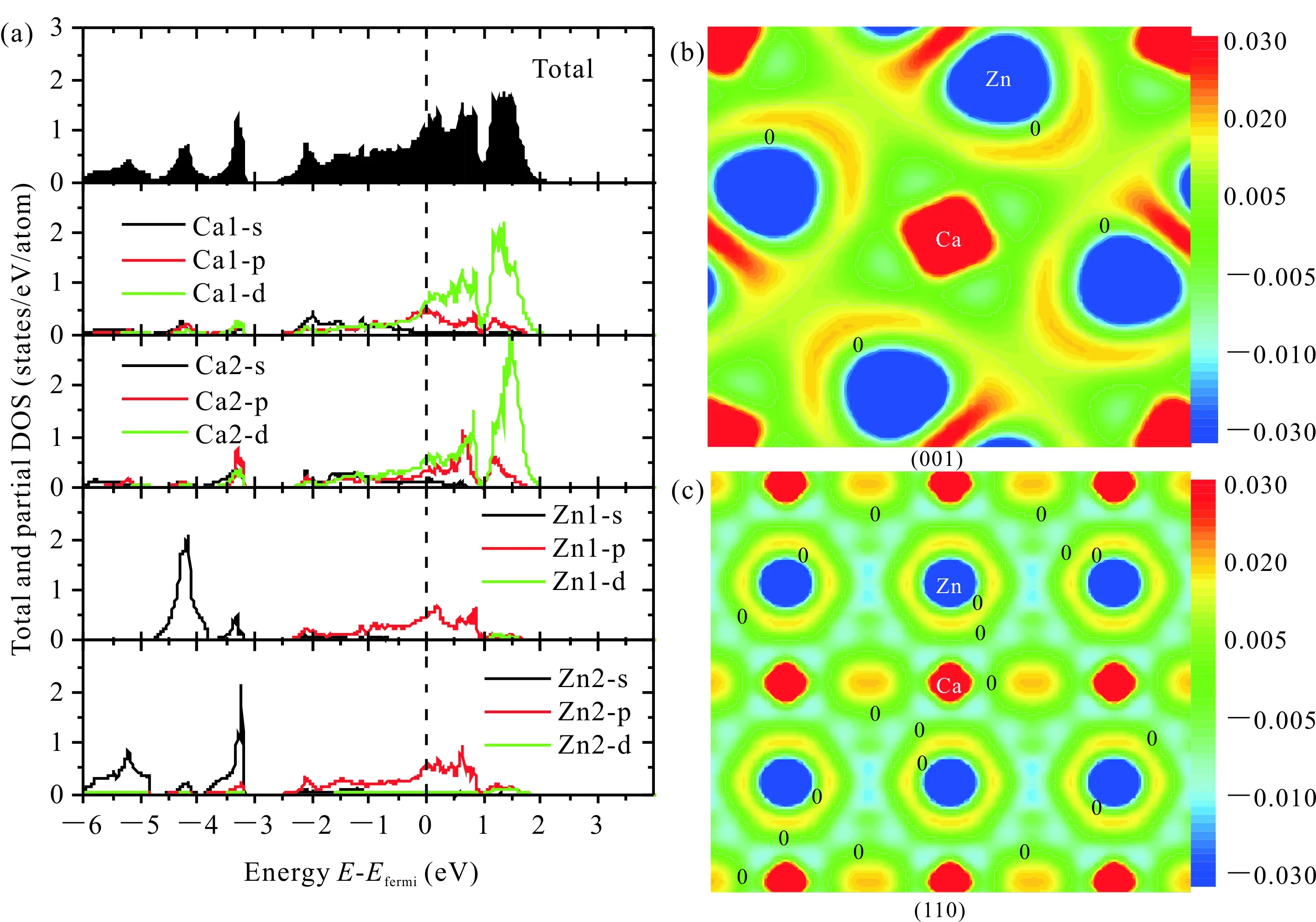
(a)電子態密度，(b) (001)面，和(c) (110)面(a) electronic density of state,(b) (001) plane and (c) (110) plane圖4 Ca5Zn3的電荷密度差Fig.4 Charge density difference of Ca5Zn3

2.4 熱物理性能

Ca5Zn3化合物的德拜溫度為202 K。平均聲速為2 097 m/s，縱向聲速為3 072 m/s， 橫向聲速為1 901 m/s (表3)。利用德拜模型[18-21]，結合第一性原理總能量的計算結果，計算了Ca5Zn3化合物在0—1 000 K溫度范圍、0—10 GPa壓強范圍內的熱物理性質(圖5)。由圖5a可知，化合物的體積隨著溫度的升高而增加，但是隨著壓強的增加則降低。并且隨著壓強的越來越大，體積減小的幅度越來越小，說明原子間的作用力也越來越大。圖5b給出了體積模量隨溫度和壓強的變化關系，隨著溫度的升高，體積模量有所下降，但是隨著壓強的增加，體積模量也在增加。圖5c表示熱膨脹系數隨著溫度的升高而增加，隨著壓強的增大而熱膨脹系數增加的幅度降低。在6 GPa以上時，隨著溫度的上升，熱膨脹系數增加的幅度極小。表明在高壓下，熱膨脹系數變化小，體積膨脹不明顯。圖5d展示的是定容熱容隨溫度和壓強的變化關系，在0—300 K區間，定容熱容急速增加，在300—400 K區間，等容熱容的上升趨勢變緩，在400 K以上，已經接近等容熱容的極限值，即杜隆珀蒂極限。

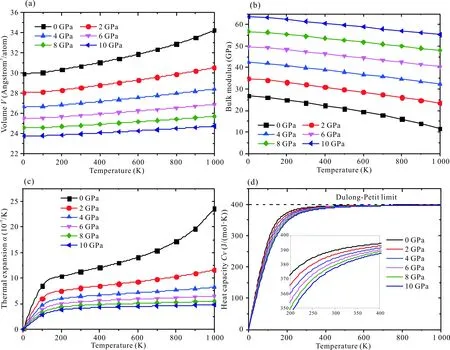
圖5 Ca5Zn3的(a)體積，(b)體積模量，(c) 熱膨脹系數和(d)等容熱容隨溫度和壓強的變化Fig.5 Change of (a) volume,(b) bulk modulus,(c) thermal expansion and (d) heat capacity of Ca5Zn3 with the temperature at various pressures

3 結論

1)具有Cr5B3型的Ca5Zn3形成焓最低，是最穩定的結構，與前人的實驗結果一致。

2)彈性常數的計算值顯示其滿足四方晶系的力學穩定性標準，計算得到了體積模量、剪切模量、楊氏模量以及B/G值，B/G值顯示該化合物呈現韌性特征。楊氏模量呈現各向異性。

3)電子態密度顯示Ca的p電子和d電子與Zn的p電子在費米能附近發生雜化效應，費米面上有態密度說明該化合物為金屬性。電荷密度差顯示Ca失去電子、Zn得到電子，與這兩種元素的電負性符合，同時呈現離子鍵特性。

4)體積、體積模量、熱膨脹系數以及定容熱容隨著溫度和壓強的變化趨勢說明，隨著壓強的增加、體積變小，體積模量變大、熱膨脹系數變小，定容熱容在低溫下變小，高溫下趨于一致。