滲流應力作用下層理巖體穩定性數值分析

劉遠楨

(貴州省機場集團有限公司，貴陽 550005)

1 概 述

巖體強度在很大程度上主要由巖體間的結構面控制，然而層理是一種較為常見的結構面，當巖體中的層理面由于滲流有孔隙水壓力作用時，這一作用將會對巖體的強度產生一定影響[1]。在巖體系統中，存在大量的地下水作用，通過物理、化學和力學等作用改變巖體的內部結構，這些作用將會給巖體施加靜水壓力和動水壓力，這些滲流現象表現出巖體系統內的滲流場對應力場的影響作用[2]。因此，研究含層理巖體中滲流場對應力場之間的相互作用具有一定的理論意義。

此外，在進行層理巖體的變形和穩定分析時，對滲流影響的評估也非常重要，且存在較大困難。一方面的主要原因在于滲流產生滲透壓力，減少層理面上的有效法向應力，從而影響巖體的變形和穩定；另一方面滲流又具有對應力和變形很強的依賴性，巖體在荷載荷載作用后，由于應力場的逐漸改變和層理法向及切向的應力逐漸增大，將會引起巖體中孔隙或層理張開度發生變化，從而巖體的滲流通道將發生變化，層理中滲流的流速和流體壓力將重分布[3]，這種作用將會使變形和滲流存在較為復雜的耦合作用。巖體中的水對巖體具有物理化學和物理力學等各種作用，前者表現為水的存在降低了巖體的強度參數和變形參數，地下水的軟化使巖土黏結力和摩擦力減小、變形參數改變、抗壓強度降低等[4]；后者表現在地下水壓力使有效正應力減小、增加滲流力及靜水壓力等。對于孔隙介質如表現為連續介質塊體和很破碎的巖體，滲流力作為一種體積力作用在巖體上；對于層理巖體塊體是相對不透水的情況下，水作為一種面力作用在結構面上，使巖體更容易沿結構面發生破壞。

鑒于此，本文基于等效連續介質模型和Louis經驗公式，從宏觀上建立能夠表征層狀邊坡耦合特性的各向異性巖體滲流應力耦合模型，同時對本文的耦合方程模型進行數值計算，分析層理滲流應力耦合規律，研究結果可為類似工程應用提供一定的參考依據。

2 層理巖體滲流應力耦合模型

已有研究表明，在考慮層理作用時，假設層理巖體的變形為彈性變形；不考慮巖體損傷、破壞對滲流的影響[5]。因此，基于等效連續介質模型，通過等效彈性張量和等效滲透張量參數來表征巖體的各向異性特性，從而建立含有層理巖體的滲流應力耦合作用關系模型，具體情況如下。

2.1 應力控制方程

在分析層理巖體的受力情況時，假定為平面問題，則平衡方程為：

σij,j+Fj=0 (i,j=1,2)

(1)

式中：σij,j為j方向上的應力張量；Fj為體積力。

同時考慮孔隙水壓力作用下巖體本構方程為：

(2)

幾何方程為：

εij=(Ui,j+Uj,i)/2

(3)

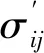
同理由彈性力學可知，對于二維平面應變問題，其剛度矩陣[D]可由各向異性的工程彈性常數進行表示，公式如下：

(4)

(5)

式中：Ei(i=1,2)為巖體在i方向的等效彈性模量；νi(i=1,2)為巖體在i方向的等效泊松比；G12為等效剪切模量。

2.2 滲流連續性方程

在分析滲流問題時，近似看作平面二維滲流問題，分析時不考慮滲流水的可壓縮性。因此得到穩定條件下的滲流連續性方程為:

(6)

2.3 耦合作用方程

研究表明，滲流應力耦合作用主要體現在表征單元體的滲透系數與應力(應變)間的相互關系，該關系是研究滲流應力耦合問題的核心[6-9]，但目前尚沒有形成統一的理論。其中Louis經驗公式僅含有一個耦合參數，該經驗公式不僅形式簡單，而且能夠反映應力與滲透系數的非線性關系，是目前在工程中應用較為廣泛的公式。

在平面應變條件下，研究各向異性巖體滲流應力耦合問題，三向應力狀態下復雜程度較大。研究表明，層理巖體在三向應力作用下以垂直于層理的方向應力對滲流作用起主導控制[10]。考慮實際巖體的層理呈密集分布，且法向上的層理分布較為稀疏，與垂直平面的相比較，平面內結構面的法向應力成為影響層理滲流的主要因素。因此，本文基于Louis經驗公式，將層理巖體的主滲透系數表示為矩陣形式，即：

(7)

式中:K11、K22分別為沿層理面和垂直于層理面方向的初始等效滲透系數；22、11分別為對應于K11、K22所在方向的法向應力，可通過應力矢量的坐標變化求得；α、β分別為Biot系數和滲流耦合作用參數，可通過室內試驗或查閱相關文獻確定，本文計算時，均取α=1,β=0.1。

2.4 層理巖體的穩定性判別式

為確定層理巖體在極限平衡狀態下的穩定性，本節對層理巖體的穩定性判別式進行推導，具體情況如下。圖1為含層理巖體單元的受力狀況。

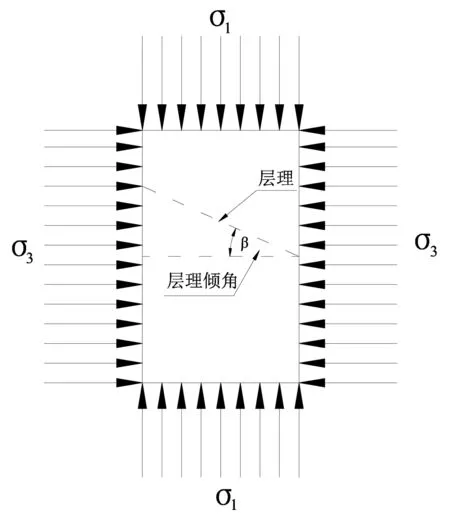
圖1 計算簡圖

由圖1可知，當層理面處于穩定狀態和極限平衡狀態時，由Mohr-Coulomb強度準則可得，巖體層理面上的剪應力應滿足剪切強度要求，即：

|τ|≤cj+σtanφj

(8)

式中：cj、φj為層理面上的黏聚力、內摩擦角；當層理巖體處于極限平衡狀態時，式(8)取等號。

式(9)、式(10)分別表示層理面上的正應力與切應力與最大主應力和最小主應力之間的應力狀態關系式。

自相關矩陣Rxx的特征結構決定了LMS算法的收斂性，當特征值相差很大時，算法收斂速度很慢，同時受輸入信號的功率變化的影響。

(9)

(10)

聯立式(8)、式(9)、式(10)得：

σ1sinβcosβ-σ3sinβcosβ≤σ1sin2βtanφj+σ3cos2βtanφj+cj

(11)

將式(11)兩邊移項整理得：

σ1sinβ(cosβtanφj-sinβ)+σ3sinβ(cosβ+sinβtanβ)+cj≤0

(12)

運用三角函數運算法則簡化得出無滲流狀態下的穩定性判別式為：

σ1cosβsin(φj-β)+σ3sinβcos(φj-β)+cjcosφj≤0

(13)

當考慮層理面內含有孔隙水壓力時，穩定性判別式為：

σ1cosβsin(φj-β)+σ3sinβcos(φj-β)+cjcosφj-pwsinφj≤0

(14)

式中的符合含義同上。當式(14)成立時，則層理巖體處于穩定狀態；相反當式(14)不成立時，層理巖體將失去穩定性。

3 數值模型與驗證

3.1 數值模型的建立

為研究本文公式的合理性與適用性，基于實際工程巖體芯樣分布情況，本文選用含有30°層理傾角的灰巖進行驗證，其巖體試樣的基本參數如下：彈性模量E=5.272GPa,泊松比為0.27，重度為26.4 kN/m3，飽和重度為27 kN/m3，黏聚力為12.72 kPa，內摩擦角為49.5°，抗拉強度為7.41 kPa；層理傾角為30°，層理面上黏聚力為0 kPa，內摩擦角為40°。

基于上述層理巖體的基本物理指標，由式(7)得到模型在滲流應力場下的主滲透系數，采用Midas GTS NX數值模擬軟件建立滲流應力耦合模型，得到滲透應力作用下的層理巖體模型，見圖2。

圖2 數值分析模型

3.2 試驗結果分析

為研究滲流應力作用下，層理巖體的滲流場和應力場的分布情況，本文選取荷載應力為q=10 kN/m、q=50 kN/m的兩種類似進行數值分析，得到相應的總水頭、總位移以及剪應變云圖，具體情況見圖3-圖5。

圖3為層理巖體在荷載作用下的滲流場水頭云圖。由圖3可知，在荷載作用下層理巖體的總水頭場呈層狀結構分布，上部水頭最大，底部水頭最小，由上至下逐漸減小。

圖3 滲流場下的總水頭

圖4為荷載10和50 kN/m作用下層理巖體總位移場分布情況。由圖4可知，在小荷載作用下的總位移在底部最大，在大荷載作用下的總位移在層理巖體的頂部。當荷載10 kN/m作用時，最大位移區達到總位移場的2.3%；當荷載50 kN/m作用時，最大位移區達到總位移場的0.8%。這說明隨著荷載作用的增加，最大位移場的作用位置發生了變化，由底部轉向頂部，在實際工程中應該注意這種變化帶來的影響。

圖4 不同荷載作用下層理巖體的總位移場

圖5為在荷載10和50 kN/m作用下層理巖體剪切應變分布情況。由圖5可知，在荷載作用下的剪應變分布主要集中在層理面的兩側，但均未出現最大剪應變區。這說明在這兩種荷載作用下，層理巖體沿層理結構相對較少，從層理巖體的位移上看，該巖體處于穩定狀態。

圖5 不同荷載作用下層理巖體的剪應變場

為驗證本文建立模型的適用性，結合式(14)與數值模擬進行擬合，計算出層理巖體的安全系數，計算結構見表1。

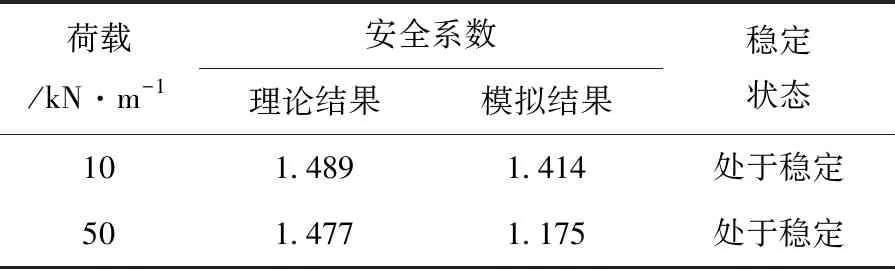
表1 安全系數計算結果

由表1可知，通過量取最大位移處的孔隙水壓力代入公式進行計算并與數值模擬得出的安全系數值。結果表明：①30°層理巖體在滲流和不同大小應力作用下的變形位移是不一樣的，隨荷載作用的增大，位移逐漸由下部上移；②相對于數值模型結果，理論計算與模擬結果基本相同，理論結果偏安全。因此，本文建立的模型適用性較強，可應用于類似工程。

4 結 論

本文對含有層理巖體的滲流應力作用進行較為詳細的分析，建立了相應的理論模型。采用Midas GTS NX數值軟件建立數值模型進行驗證，得到的主要結論如下：

1) 通過等效連續介質模型和Louis經驗公式，建立了層理巖體滲流應力耦合模型，該模型能反映層理巖體在滲流應力作用下的變形特征，具有一定的理論參考價值。

2) 基于巖體極限平衡狀態推導的30°層理巖體滲流應力耦合的穩定性情況判別式的計算結果與數值計算結果較好吻合，具有一定現實意義。

3) 根據實際工程層理巖體，建立了相應的數值模型，對現有模型進行驗證，適用性較好。同時發現隨著荷載作用增大，位移場作用發生轉移，由層理巖體的底部向頂部轉移。

4) 研究結果可為類似工程提供一定的參考依據，具有一定的工程應用價值。但受到計算方法和數值模擬的局限，具體的結果還有待作進一步應用和推廣。