基于改進A-Star算法的隱身無人機快速突防航路規劃
張哲,吳劍,2,*,代冀陽,應進,何誠
1. 南昌航空大學 信息工程學院,南昌 330063 2. 北京航空航天大學 可靠性與系統工程學院,北京 100083
在現代戰爭中,隨著隱身與反隱身技術的快速發展,現代戰區立體防空體系部署日益嚴密,飛行器僅僅依靠傳統突防模式下的航跡規劃技術實現戰區突防已經越來越難[1]。如何在嚴密的組網雷達系統威脅下,為隱身無人機快速地規劃出具有高安全性的突防路線是當前面臨的一個重大難題[2-4]。
雷達的探測能力與目標的雷達散射截面(Radar Cross Section,RCS)有關。由于隱身無人機全向的部分角域具有較小的RCS值,通過調整隱身無人機的姿態角,使得這些具有較低RCS值的角域面向雷達時,能夠大幅度地降低雷達檢測概率,從而保證隱身無人機的安全突防[5]。此外,現有雷達系統只有在多次掃描獲取的目標信號滿足一定準則時,才會做出有效的判決。因此,在復雜的戰場環境下,結合飛行器全向的動態RCS特點和雷達發現準則這2個因素,選用合適的突防飛行路線,便能夠保證隱身無人機能夠在復雜的戰場環境中實現安全、快速突防。
目前大部分航路規劃研究主要集中在離線規劃、在線規劃或是航跡優化等方面[6-8],通常將雷達威脅以固定的威脅區域放置于二維或三維空間進行討論,較少考慮飛行器全向RCS值及雷達發現準則等因素,這些研究顯然無法滿足隱身無人機在復雜環境中的突防需求[9]。文獻[10-13]通過建立動態RCS模型來獲取目標更準確的全向RCS值,從而更好地反映目標時刻所處的威脅狀態。文獻[14-15]分析雷達工作機理,以一定掃描周期內的發現概率均值來體現目標被確認發現的概率。這兩部分的研究為飛行器實現快速、安全的戰區突防奠定了重要的理論基礎。
本文結合隱身無人機突防過程中的動態RCS特性和雷達發現準則,建立了隱身無人機運動學模型和組網雷達探測概率模型。充分考慮了所規劃航路的快速性和安全性,采用A-Star算法進行突防航跡規劃,對隱身航路的實際需求進行了算法改進:① 在A-Star算法搜索過程中引入了含有加權因子的多層變步長搜索策略;② 在算法搜索節點中添加隱身無人機的姿態角信息;③ 在 航跡節點中考慮雷達的秩K融合準則[16],以此來判斷新航跡點的可行性。分別在單雷達和組網雷達系統環境下,運用改進A-Star算法與傳統A-Star算法進行仿真實驗對比,結果表明在復雜的組網雷達威脅環境下,改進算法用于隱身無人機,能夠實現其快速、安全的戰區突防,從而進一步驗證了所提出的改進A-Star算法的有效性。
1 隱身無人機突防過程建模與分析
在現代空戰的防御體系中,組網雷達系統根據空中目標的RCS,能夠從多個站點對指定的空域進行全面探測,對整個空域范圍內的目標實現全方位的定位、識別和跟蹤。因此,組網雷達的廣泛應用,極大程度地提高了飛行器在空域內的突防難度。
隱身無人機在設計時,通常根據雷達的幾種波段,對機頭、機身和尾翼等雷達重點照射角域進行RCS減縮,這樣能夠大大減小雷達的探測概率,降低系統的戰斗效能,從而提高隱身無人機的突防能力和生存能力。
1.1 隱身無人機運動學模型
隱身無人機在飛行中為了節省燃油消耗,更好地展現隱身性能實現戰區突防,通常會在固定高度保持巡航狀態,盡量不做出大規模機動動作。結合隱身無人機的運動學特性,對其進行建模分析。
本文將隱身無人機認為是一個帶有姿態信息的質點,以恒定的速度v在固定高度h下做小機動動作或轉彎飛行。因此建立隱身無人機的運動學模型,即
(1)
式中:x、y分別為無人機在地理坐標系中的位置;φ為無人機的航向角;θ為無人機的滾轉角;v為無人機的飛行速度;g為重力加速度。
考慮無人機在空域水平飛行中的小機動動作和轉彎運動,由于保持定高飛行模型,因此隱身無人機的運動狀態如圖1所示。
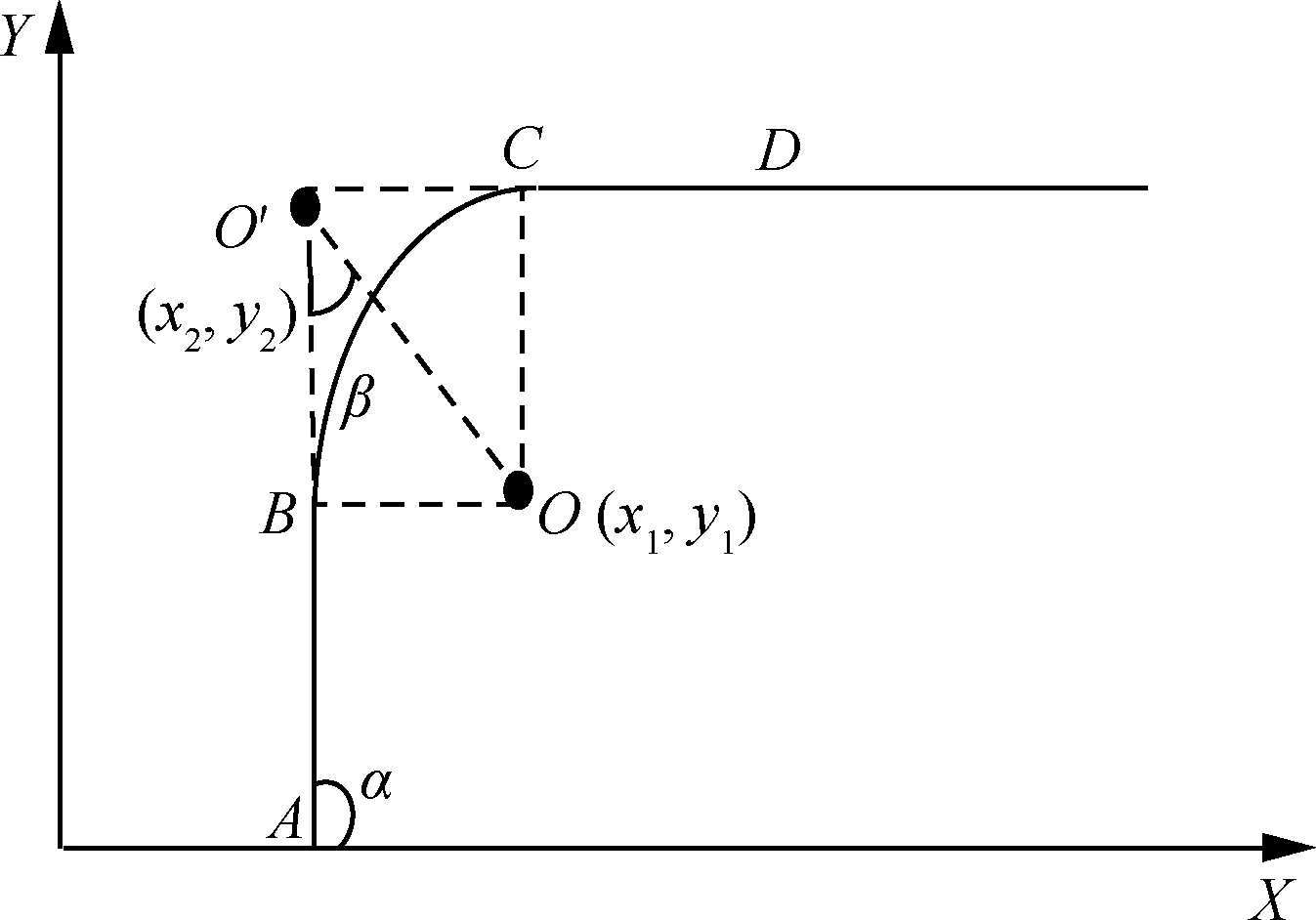
圖1 隱身無人機的運動狀態Fig.1 Movement state of stealth UAV
假設已給出直線段的路線參數和轉彎半徑,由圖1可知,線段AB和線段CD分別為無人機轉彎前的飛行路線。圓弧BC為無人機轉彎過程中的軌跡。因此,圓弧的中心坐標可以表示為
(2)
式中:(x1,y1)為點O的坐標;O′為AB和CD兩條線段延長線的交點;b為AO′與BO′長度的比例系數;α為航線與水平方向的夾角;β為航跡延長線與轉彎半徑延長線的夾角。
無人機在轉彎過程中由于滾轉角θ的變化,會增大被雷達所探測到的概率,從而大大提高了隱身突防難度。因此,為了保障無人機轉彎過程中的安全,本文給出了無人機的2種轉彎飛行模式[17],并進行了以下分析:
1) 最大負載飛行模式。無人機在轉彎時保持較大的滾轉角,這樣可以保證轉彎半徑r最小,轉彎所需時間最少,暴露于雷達中的時間相對較短。
2) 最小滾轉角飛行模式。假設圖1中線段AO′和BO′是無人機飛行中相鄰的2個航線,當B點為線段AO′的中點,C點為線段O′D的中點時,無人機能夠以最大轉彎半徑保持轉彎飛行,這樣便可以在飛行過程中始終保持相對較小的滾轉角θ,大大降低了雷達系統的探測概率。
分析圖1中航線的幾何關系及式(2),可得無人機飛行中的轉彎半徑與航線段的關系式為
(3)
以rmin和rmax分別表示無人機的最小轉彎半徑及最大轉彎半徑,由式(3)計算可得無人機飛行過程中的最大轉彎半徑為
(4)
用θmax和θmin分別表示無人機飛行時的最大滾轉角和最小滾轉角,分析式(1)中無人機的運動學模型及圖1中的航線幾何關系,可以計算得到:
(5)
通過對隱身無人機運動學模型的求解,充分考慮無人機的姿態角信息,從而更好地分析隱身無人機突防的航路變化及精準計算雷達的探測概率。
1.2 動態RCS特性
隱身無人機的RCS是影響雷達探測概率的關鍵因素之一,對無人機實現戰區的隱身突防有直接的影響。一般的航跡規劃問題通常將RCS視為固定值,但在實際中并不合理。目標無人機的RCS值會根據雷達波照射方向的不同而變化,不同視線方向上的RCS具有劇烈起伏的特點。而且,某一方向上的無人機RCS的大小還與入射雷達波的頻率、雷達天線的極化方向這2個因素有關[1]。因此,無人機在進行隱身設計時,通常會在防空雷達的幾種常用波段(如S、C波段)以及水平(Horizontal and Horizontal,HH)極化和垂直(Vertical and Vertical,VV)極化方式下,對無人機的重點角域進行RCS減縮。
隱身無人機在飛行過程中,其與各部雷達相對姿態角的改變,使得雷達探測到的無人機的RCS值也會不斷變化,即呈現出動態RCS特性。為了充分利用隱身無人機的動態RCS特性進行快速突防,需要采用更完整的RCS周向數據來進行航跡規劃。本文根據數值計算和微波的實驗數據,以RCS數據表[18]作為動態RCS特性來分析。若無人機不進行頻繁大機動飛行時,可僅取水平照射一定俯仰角范圍內的數據。
1.3 雷達的探測概率
雷達系統會對指定空域進行反復掃描,在有效作用范圍內,用雷達檢測概率表示雷達在某段時間內能夠連續獲得目標信息的可能性,每次進行的空域掃描都會以一定的檢測概率來獲取目標信號。當所獲得的目標信息滿足常用的航跡準則時,雷達系統確認發現目標,并將所獲取的目標信息傳遞至系統的信息融合中心。下面分別討論在單雷達和組網雷達下系統對目標的探測概率。
1.3.1 單雷達系統的探測概率
對于給定的單雷達系統,當其檢測概率和虛警概率確定時,對無人機目標的探測概率只與無人機到雷達中心的距離和RCS值有關。在一段時間內,通過累計雷達對無人機目標的多次瞬時探測概率,可以計算得到雷達探測概率為
(6)
式中:P為雷達探測概率;Pt為瞬時探測概率;T為雷達掃描周期;t為當前時刻;Ri為無人機到第i個雷達中心的距離;σ為無人機的RCS值;c1和c2為由雷達自身性能確定的參數[1,18]。
然而在實際的突防飛行過程中,隱身無人機按照某一航路飛過雷達區域時會經歷多次雷達探測,由于每次探測時無人機的RCS值、與雷達中心的距離和姿態角均不同,造成雷達在無人機各航跡點的探測概率也不同。為了更客觀地反映隱身無人機在雷達系統探測下整個航路受到威脅的情況,將雷達系統的各次瞬時探測概率進行累加,即對式(6)中無人機探測概率作離散化處理,得到單雷達系統下的無人機探測概率為
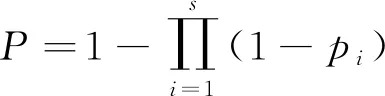
(7)
式中:s為雷達掃描次數;pi為雷達對無人機的第i次探測的瞬時探測概率。
1.3.2 組網雷達系統的探測概率
對于完整的組網雷達系統,內部各雷達的聯網可以顯著提高系統對無人機的探測概率。組網雷達系統的探測概率主要是指信息融合中心計算得出的目標發現概率。在現代的組網雷達系統中,秩K融合規則應用廣泛。因此,采用秩K融合規則對組網雷達探測概率進行深入分析。
設組網雷達系統中有M部雷達,由秩K融合規則,當系統內發現目標無人機的雷達數量超過最優檢測門限K0時,即認為雷達發現該目標,當組網雷達對無人機的融合探測概率Pd∈[0.5,0.9],組網雷達系統的融合虛警概率Pf∈[10-9,10-5]時,最優檢測門限K0的近似值為
(8)
秩K融合規則判決流程如圖2所示。每部雷達根據自身對隱身無人機的探測做出局部判斷,判決結果非0即1,取決于局部門限檢測目標是否存在。由二元假設為H0和H1,H0表示目標不出現,H1表示目標出現。因此第j個雷達的決策值dj(j=1,2,…,M)可以表示為
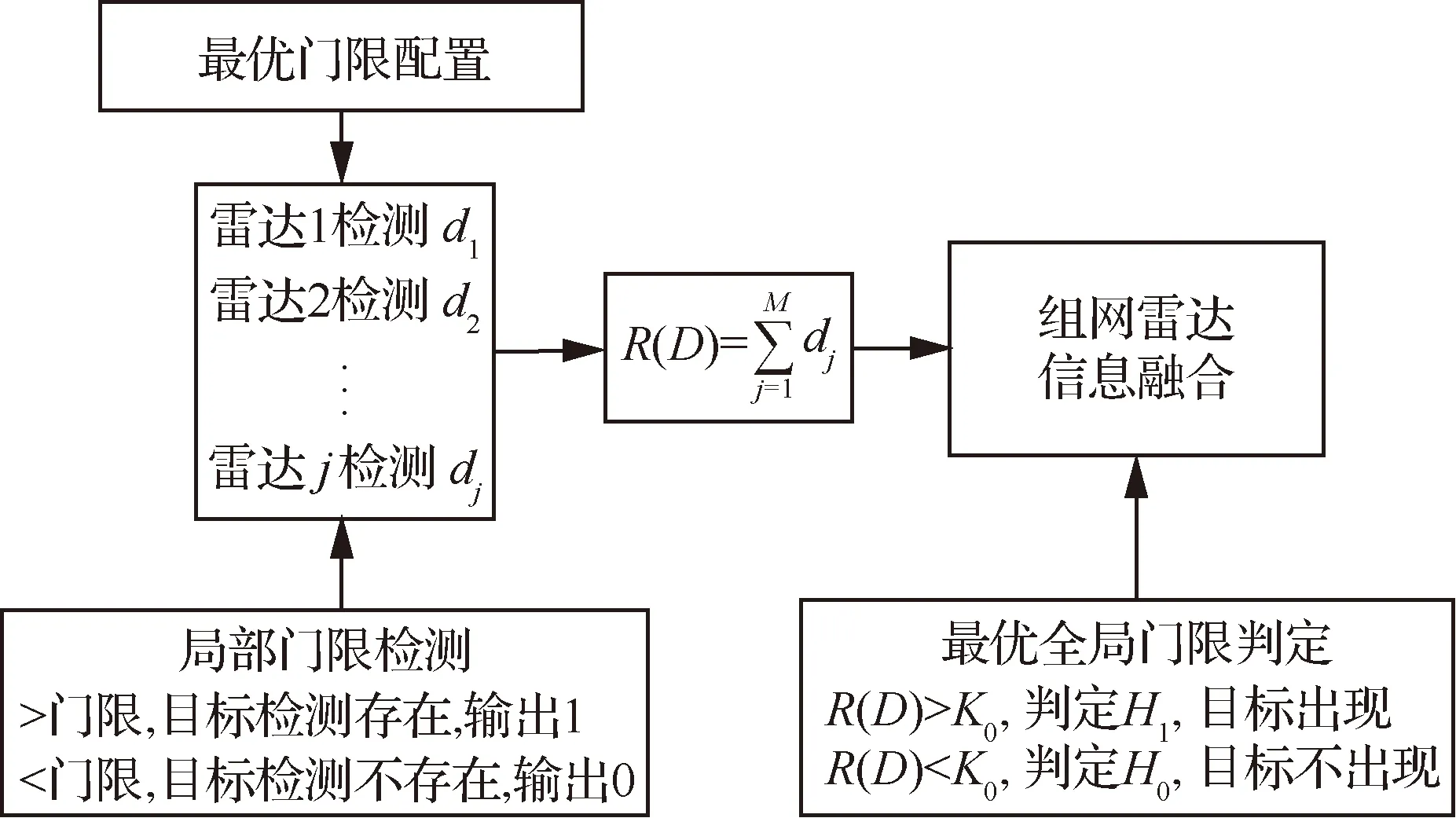
圖2 秩K融合規則判決流程Fig.2 Rank K fusion rule decision process
(9)
然后將局部判決結果傳遞至雷達系統的信息融合中心,構成全局判決空間D,即D={d1,d2,…,dM},組網雷達信息融合規則記為R,則秩K融合的判決規則R(D)可以表示為
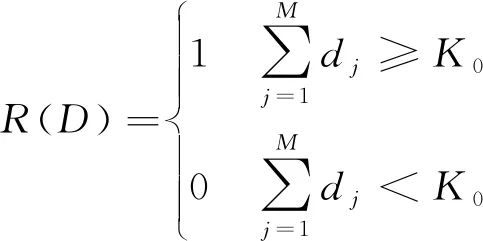
(10)
此時,組網雷達系統對無人機的總探測概率為
(11)
式中:集合S1是使融合中心判為1的局部判決向量所構成的集合,由融合規則R(D)確定;集合S0是使融合中心判為0的局部判決向量所構成的集合;Pdj為組網雷達系統內第j個雷達對無人機的探測概率。
同理可知,整個組網雷達系統的虛警概率PF為
(12)
2 突防航跡規劃算法
A-Star算法作為一種啟發式搜索算法,廣泛應用于各類智能體的路徑規劃問題中[19-21]。本文引入A-Star算法用于隱身無人機的戰區突防航路規劃,從隱身無人機航路搜索的快速性和安全性兩方面入手進行深入分析。
2.1 算法描述
在標準A-Star算法的航路搜索過程中,通過設定合適的啟發函數,全面估計待搜索區域可擴展搜索點的代價值,通過比較各點不同代價值的大小,兼顧考慮航跡點搜索的運算時間與距離代價,找出一條最優的航路。在A-Star算法中,通常利用對OPEN表和CLOSE表的操作來實現航跡點的存儲和更新。算法的尋優運算可以表示為
f(n)=g(n)+h(n)
(13)
然而采用標準A-Star算法搜索產生的航路存在以下不足:① 只能反映無人機的位置信息,無法體現隱身無人機的動態RCS特性及姿態信息;② 并且未考慮雷達探測概率,僅僅通過比較各相鄰擴展點的代價大小來判斷航跡點的可行性;③ 在航路搜索過程中未知路徑代價估值的h(n)在路徑還未被完全擴展之前無法精確計算,最終設計的路線可能不是全局最優解且運算時間較長。因此,對傳統A-Star算法進行改進,對航跡點的擴展搜索方式、步長值、新航跡點的可行性判定及運算時間等進行優化改進。
2.2 改進A-Star算法
2.2.1 無人機姿態角信息融合
結合隱身無人機的動態RCS特性,在A-Star算法節點中添加了無人機的姿態角信息。首先將A0(x0,y0)作為第1個擴展節點放入OPEN表中,由相鄰節點總代價值向待搜索區域進行擴展;然后,比較各節點的代價值大小,選取所有節點中總代價值f(n)最小的點,作為新的航跡節點An(xn,yn),同時生成新節點處的航向角φn。最后,在等高和勻速小機動飛行模式下,結合式(1),在An處父節點的滾轉角θn可表示為
(14)
式中:φn為與航跡新節點相鄰的各節點的航向角;φs為周圍節點的航向角;η為擴展搜索的步長。
此外,在對待擴展區域的搜索過程中,相鄰航跡節點之間的航向角變化需要滿足最大轉向角速度的約束,即
(15)
因此,可以得到擴展搜索過程中在An處無人機飛行時的姿態角信息(θn,φn),再結合式(6)~式(8),便可計算出各時刻An節點處的雷達探測概率Pt。
2.2.2 多層變步長策略
標準A-Star算法利用OPEN表進行尋優運算時,無法對待搜索區域內未知路徑的代價值進行準確的計算,通常采用當前節點與下一步的目標擴展節點的直線距離來估計,顯然無法保證這段航跡點的精度及整段航線的安全性[22-23]。因此,引入一個加權因子ω,其中ω>1,此時f(n)的表達式為
f(n)=g(n)+ωh(n)
(16)
這意味著增大了未知路徑代價在總路徑代價的占比,即增加了A-Star算法的搜索深度,防止算法陷入局部搜索的死區中,保證了最優解的質量。
為保證隱身無人機在復雜的組網雷達系統下實現快速突防,需要對傳統A-Star算法的搜索方式進行改進,來提高整個突防過程中航跡點搜索效率。因此,設計了一種多層變步長的搜索方式來進行運算尋優。
在算法搜索過程中,由第k步已擴展點Ak(xk,yk)至第k+1步可擴展點Bk(xk+1,yk+1)坐標為
(17)
式中:φi和Lj分別為拓展搜索線段間的夾角與對應弧長,即
(18)
若該元素不與B陣中的其他元素重合,不在OPEN表或CLOSE表中,則該元素可擴展至CLOSE表。變步長搜索策略的拓展過程如圖3所示。
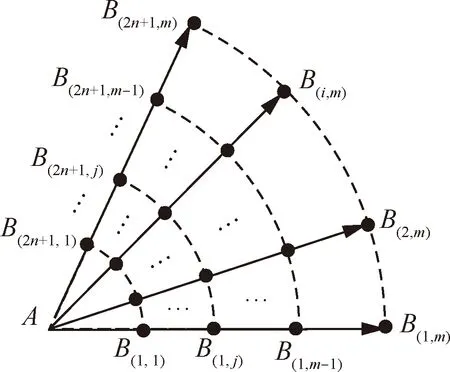
圖3 變步長搜索航跡點拓展過程Fig.3 Variable step size search track point expansion process
2.2.3 新航跡點的可行性判定
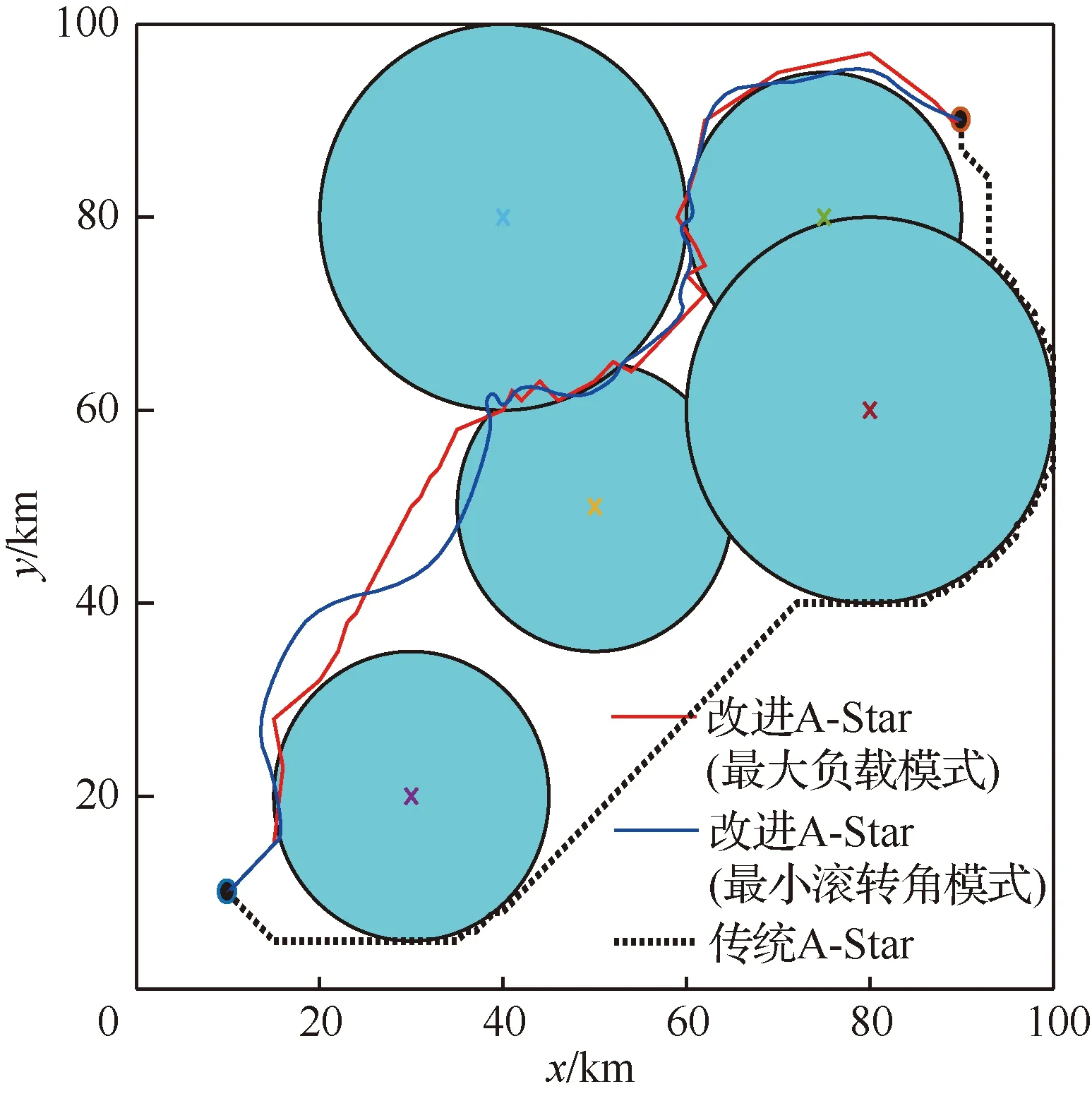
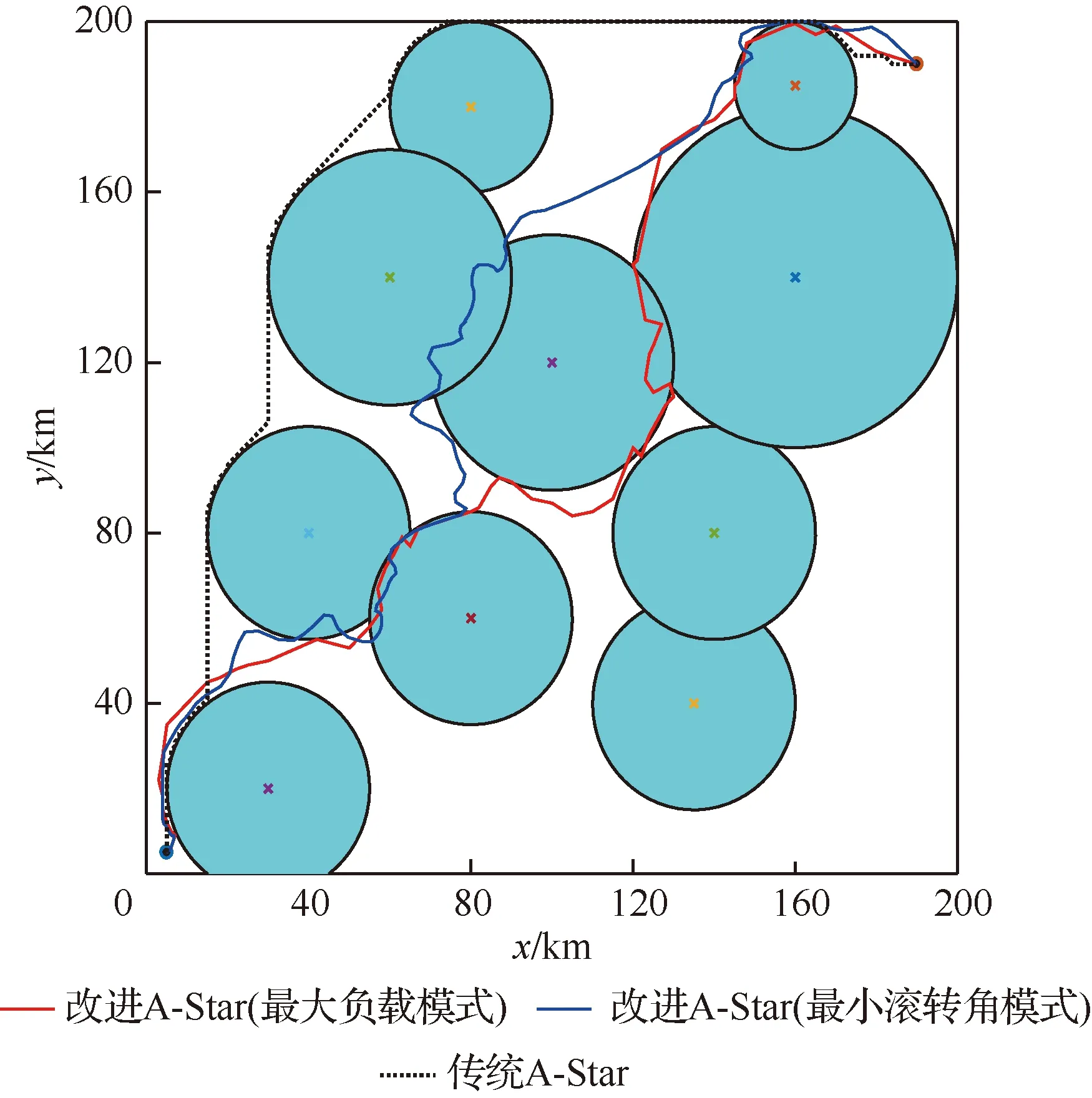
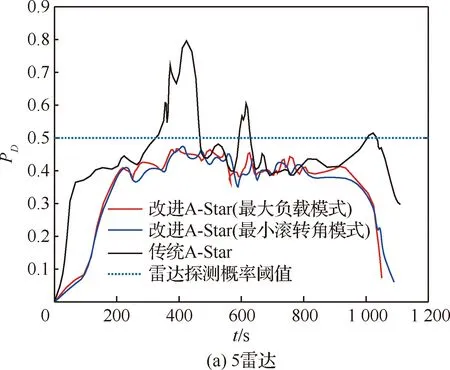
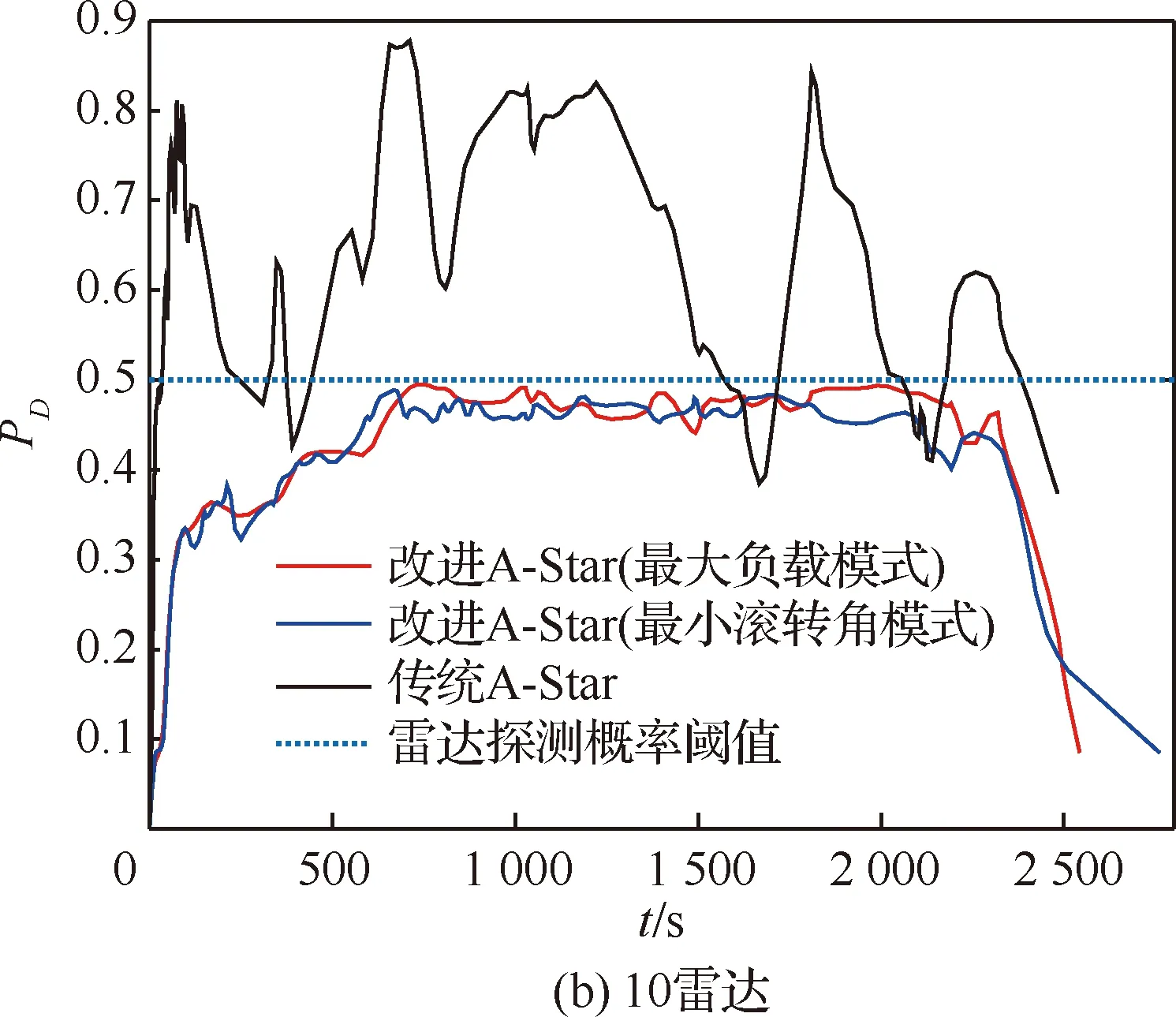
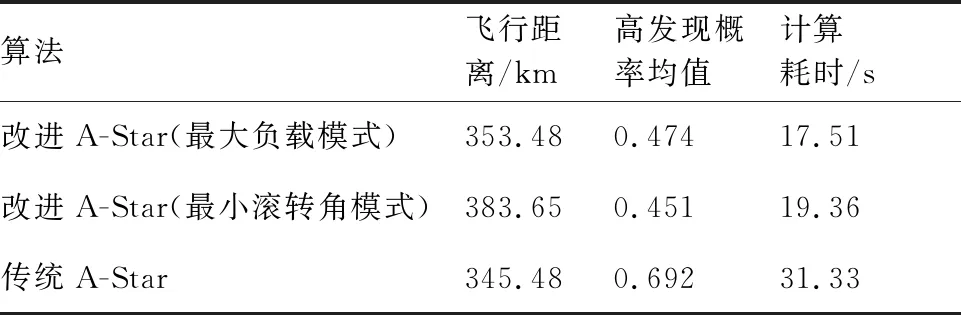
改進A-Star算法在對待擴展區域的搜索過程進行當前航跡節點An(xn,yn)擴展時,生成其相鄰節點及其航向角和滾轉角,由秩K融合規則的式(10)和式(11),計算對應節點該時刻的雷達探測概率;然后,結合當前節點與之前相鄰節點的雷達探測概率,計算得到該航跡段上的探測概率Pn;最后,根據突防安全性要求,設定一個概率閾值Pc,若Pn 綜上分析,可以給出改進A-Star算法的詳細流程如圖4所示。 圖4 改進A-Star算法的流程圖Fig.4 Flowchart of improved A-Star algorithm 為了驗證模型及改進算法的有效性,在單雷達和組網雷達的戰區防空系統下,分別采取最大負載飛行和最小滾轉角飛行這2種轉彎飛行模式,隱身無人機以速度v為500 km/h,高度為1 000 m,b=2,符合實際無人機運動狀態,在勻速定高飛行下實現低空戰區突防,并通過限制航向角φ使得無人機僅做小機動動作。所有雷達均采用秩K融合準則判定及計算無人機的探測概率,K0值由雷達數M確定,取s=3,改進A-Star算法搜索過程中的加權因子ω=1.5,初始的拓展搜索角度為6°,步長為2。設雷達對無人機的探測概率閾值Pc為0.5,當Pn>0.4時為雷達高發現的概率狀態,用來評估該航跡段的安全程度,在仿真實驗中,RCS表選取S波段HH極化數據,可得到某型隱身無人機的全向RCS數據,如圖5所示。 圖5 某型隱身無人機的全向RCS曲線(S波段HH極化)Fig.5 Omnidirectional RCS curve of a stealth UAV (S-band HH polarization) 設定100 km×100 km的無人機突防區域,單雷達系統中雷達的坐標為(50,50) km,無人機飛行起始點為(10,10) km,目標點為(80,80) km,分別采用改進A-Star算法和傳統A-Star算法進行無人機隱身突防仿真,如圖6所示。單雷達系統下的隱身無人機飛行數據見表1。 圖6 單雷達系統下的突防仿真結果Fig.6 Penetration simulation results under single radar system 表1 單雷達系統下飛行仿真數據Table 1 Flight simulation data under single radar system 由圖6中2種方法的仿真結果比較及表1的無人機飛行數據統計可知,在單雷達系統的戰區突防環境下,改進A-Star算法通過控制隱身無人機在各航路點上的飛行姿態,實現了更有效和相對安全的航路突防。 由于組網雷達系統內的各種雷達覆蓋范圍互有重疊,因此相較于單雷達系統,其信息融合系統能夠得到質量更好地目標航跡,極大提高了系統對目標的反低空突防能力。為了進一步驗證改進A-Star算法的有效性,設定組網雷達系統中雷達數量分別為3、5和10這3種情景,各雷達性能參數略有不同,對隱身無人機進行戰區突防仿真。 3.2.1 3雷達系統 在100 km×100 km的突防區域中,各雷達位置分別為:雷達1 (80,40) km,雷達2 (30,80) km,雷達3 (50,50) km。無人機飛行的起始點坐標(10,10) km,目標點坐標(90,90) km。分別采用改進A-Star算法和傳統A-Star算法進行無人機隱身突防仿真,如圖7所示。3雷達系統下的隱身無人機飛行數據見表2。 由圖7中仿真結果及表2中的飛行數據統計可知,在3雷達系統的戰區突防環境下,改進A-Star算法可以在雷達威脅密度較大的區域中實現隱身無人機安全突防。與傳統A-Star算法相比,改進算法通過對各航跡點的變步長搜索,能夠更加精確地調整隱身無人機的姿態,從而控制整段航路上各處的RCS值,得到更短的飛行距離和安全的航跡節點,實現快速、安全的戰區突防航路規劃。 圖7 3雷達系統下的突防仿真結果Fig.7 Penetration simulation results under three radars system 表2 3雷達系統下飛行仿真數據Table 2 Flight simulation data under three radars system 3.2.2 5雷達系統 在100 km×100 km的突防區域中,各雷達位置分別為:雷達1 (50,50) km,雷達2 (30,20) km,雷達3 (75,80) km,雷達4 (40,80) km,雷達5 (80,60) km。無人機飛行的起始點坐標為(10,10) km,目標點坐標為(90,90) km。分別采用改進A-Star算法和傳統A-Star算法進行無人機隱身突防仿真,如圖8所示。5雷達系統下的隱身無人機飛行數據見表3。 表3 5雷達系統下飛行仿真數據Table 3 Flight simulation data under five radars system 圖8 5雷達系統下的突防仿真結果Fig.8 Penetration simulation results under five radars system 3.2.3 10雷達系統 在200 km×200 km的突防區域中,各雷達位置分別為:雷達1 (135,40) km,雷達2 (30,20) km,雷達3 (140,80) km,雷達4 (40,80) km,雷達5 (80,60) km,雷達6 (160,140) km,雷達7 (160,185) km,雷達8 (80,180) km,雷達9 (100,120) km,雷達10 (60,140) km。無人機飛行的起始點坐標為(5,5) km,目標點坐標為(190,190) km。分別采用改進A-Star算法和傳統A-Star算法進行無人機隱身突防仿真,如圖9所示。10雷達系統下的隱身無人機飛行數據見表4。 圖9 10雷達系統下的突防仿真結果Fig.9 Penetration simulation results under ten radars system 以雷達探測概率作為突防結果的影響因素,不同環境下的組網雷達探測概率如圖10所示。 圖10 典型威脅環境下不同算法的突防威脅概率Fig.10 Penetration threat probability of different algorithms in typical threat environment 由圖8和圖9中仿真結果及表3和表4可知,在5雷達系統和10雷達系統的典型威脅環境下,由于傳統A-Star算法在航跡搜索過程中,計算得到部分航跡節點的雷達探測概率高于閾值,無法滿足航路的安全性要求。因此,傳統A-Star算法在實際的雷達威脅環境中應該是無航路規劃結果的。但是,為了進一步分析,認為被探測概率即使超過閾值,無人機仍然可以向前突防,計算得到在5雷達和10雷達威脅環境下,無人機探測概率超過閾值的飛行時間分別為209.35 s和1 940.35 s。而改進A-Star算法仍然可以在雷達威脅密度較大的區域中實現隱身無人機成功突防,且整段航路的探測概率均小于閾值。與傳統A-Star算法相比,改進算法充分利用各航跡點的變步長搜索策略和姿態變化,控制整段航路上各點的RCS值,能夠滿足隱身無人機戰區突防中快速和安全這兩點要求。 表4 10雷達系統下飛行仿真數據Table 4 Flight simulation data under ten radars system 1) 針對復雜的組網雷達系統下隱身無人機實現快速和安全的突防問題,提出了一種改進A-Star 算法的隱身無人機戰區突防航路規劃方法,并將其與傳統A-Star算法進行比較,仿真結果表明改進算法優于傳統算法。 2) 所設計的改進A-Star算法在對航跡節點的搜索過程中引入了多層變步長搜索策略和無人機的姿態角信息,加快了航路搜索的效率,體現了隱身無人機動態RCS的變化特性,為復雜戰場環境中的隱身無人機突防提供了一定的軍事應用價值。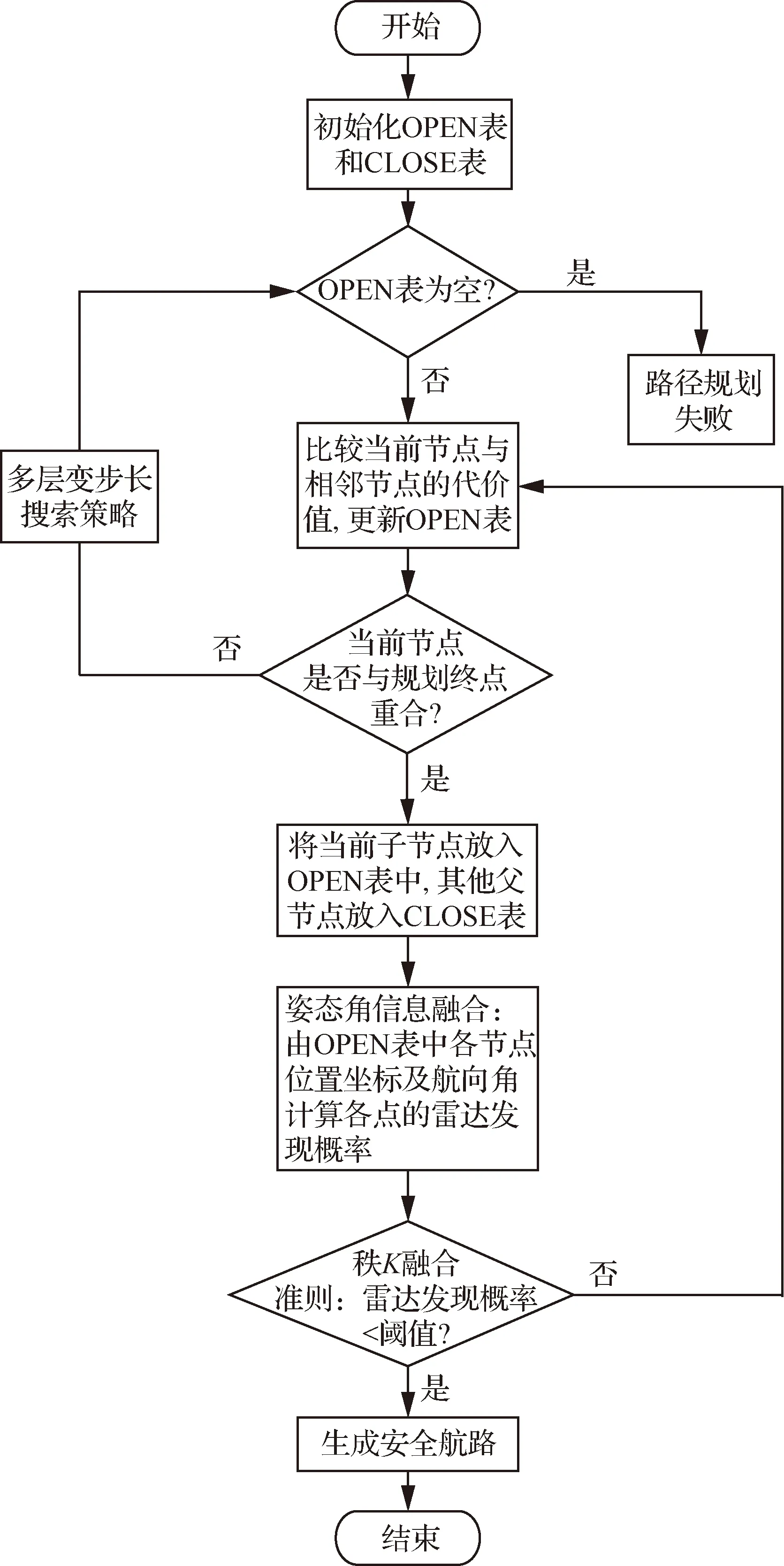
3 仿真實驗分析
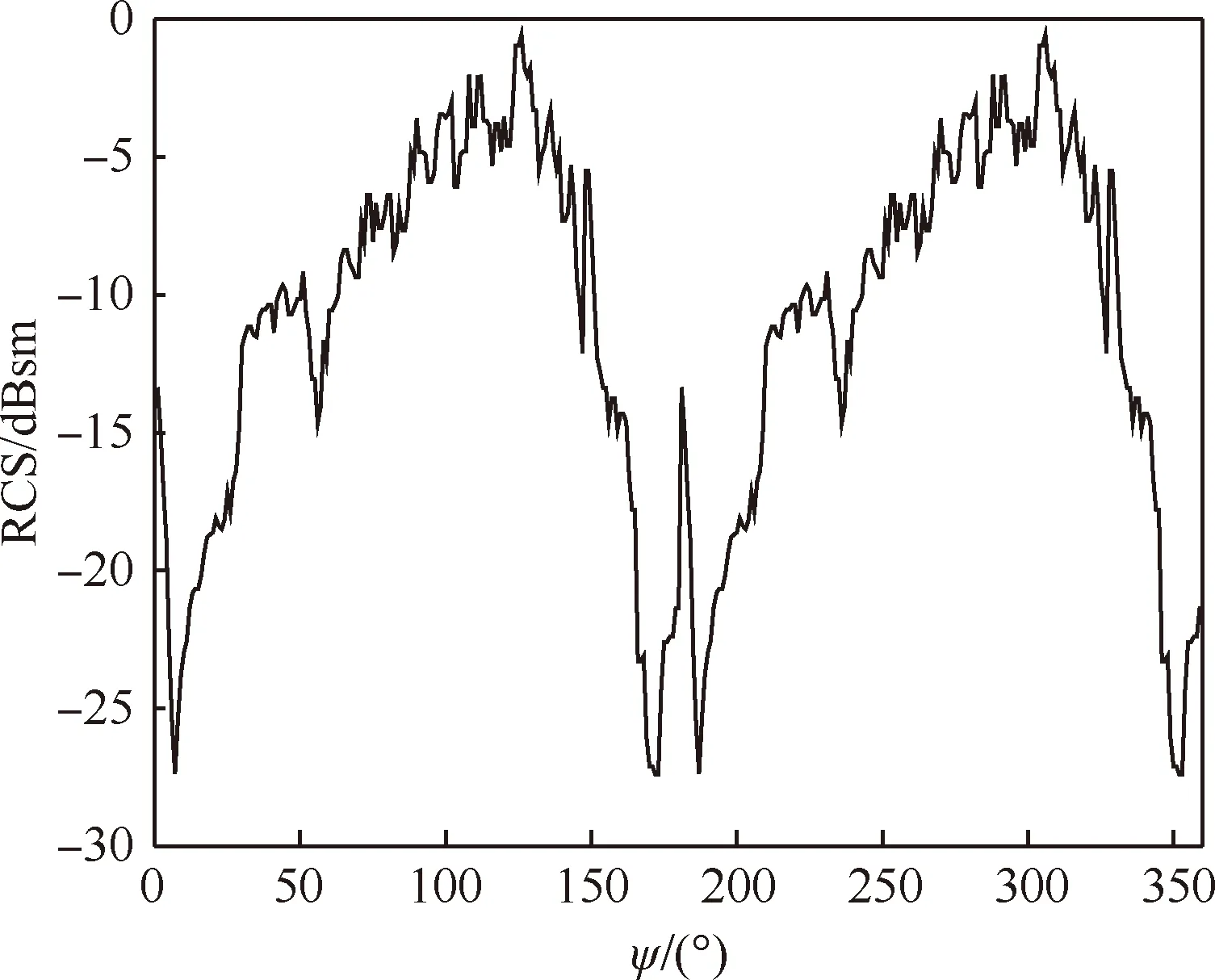
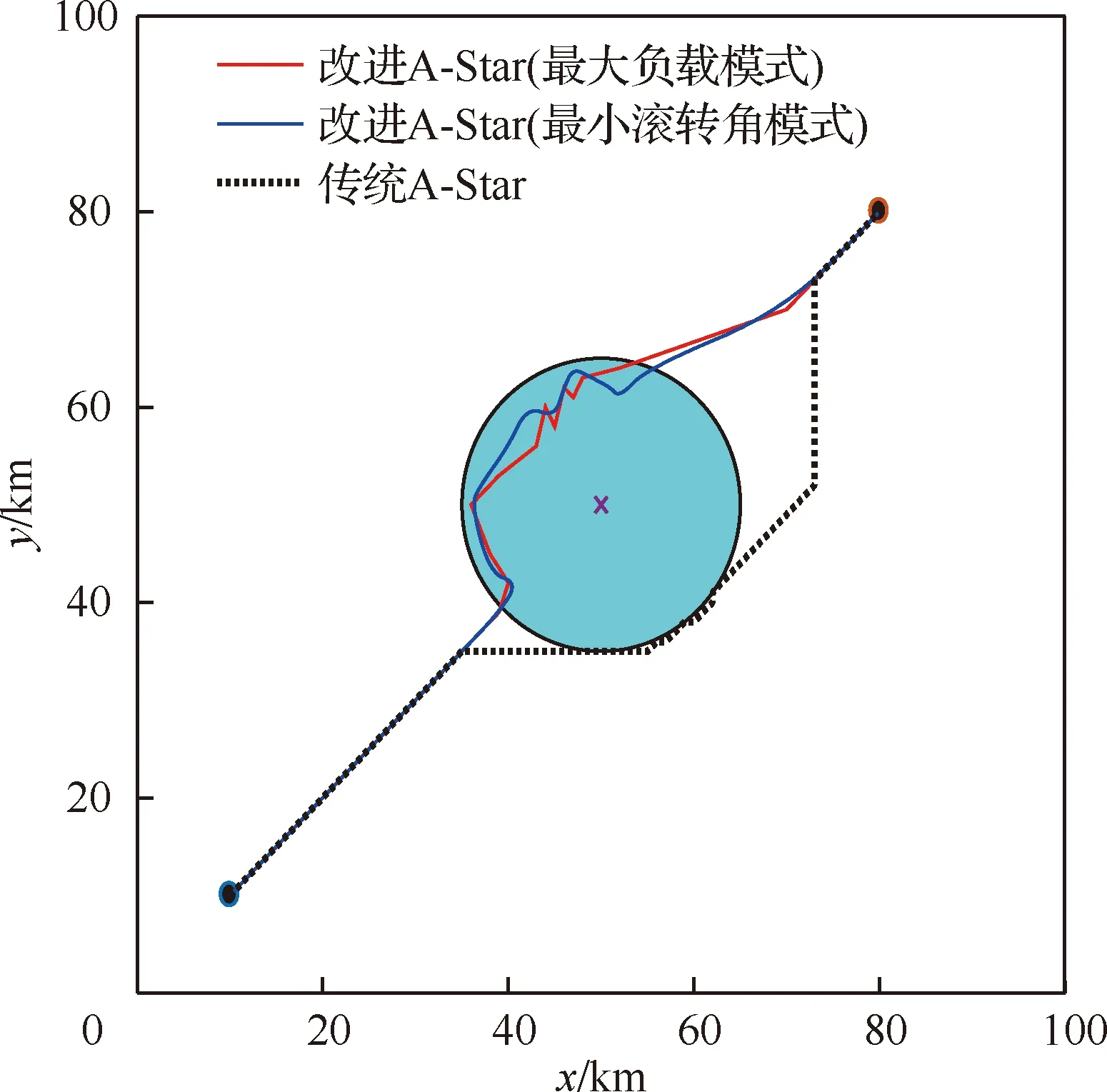
3.1 單雷達系統
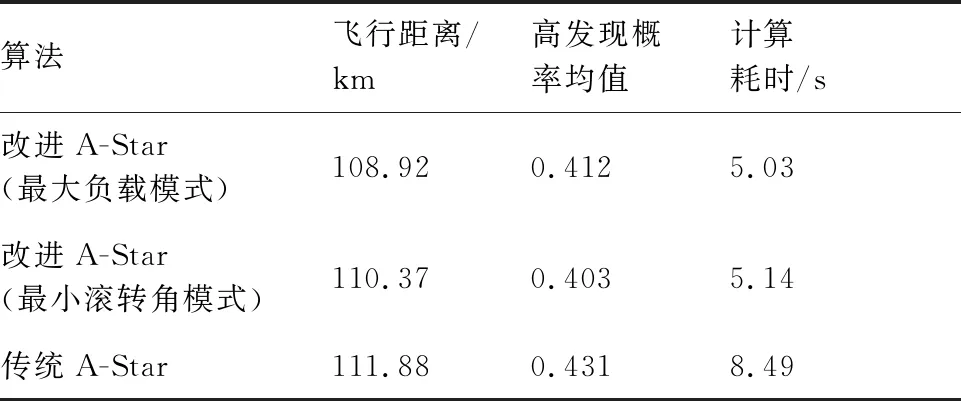
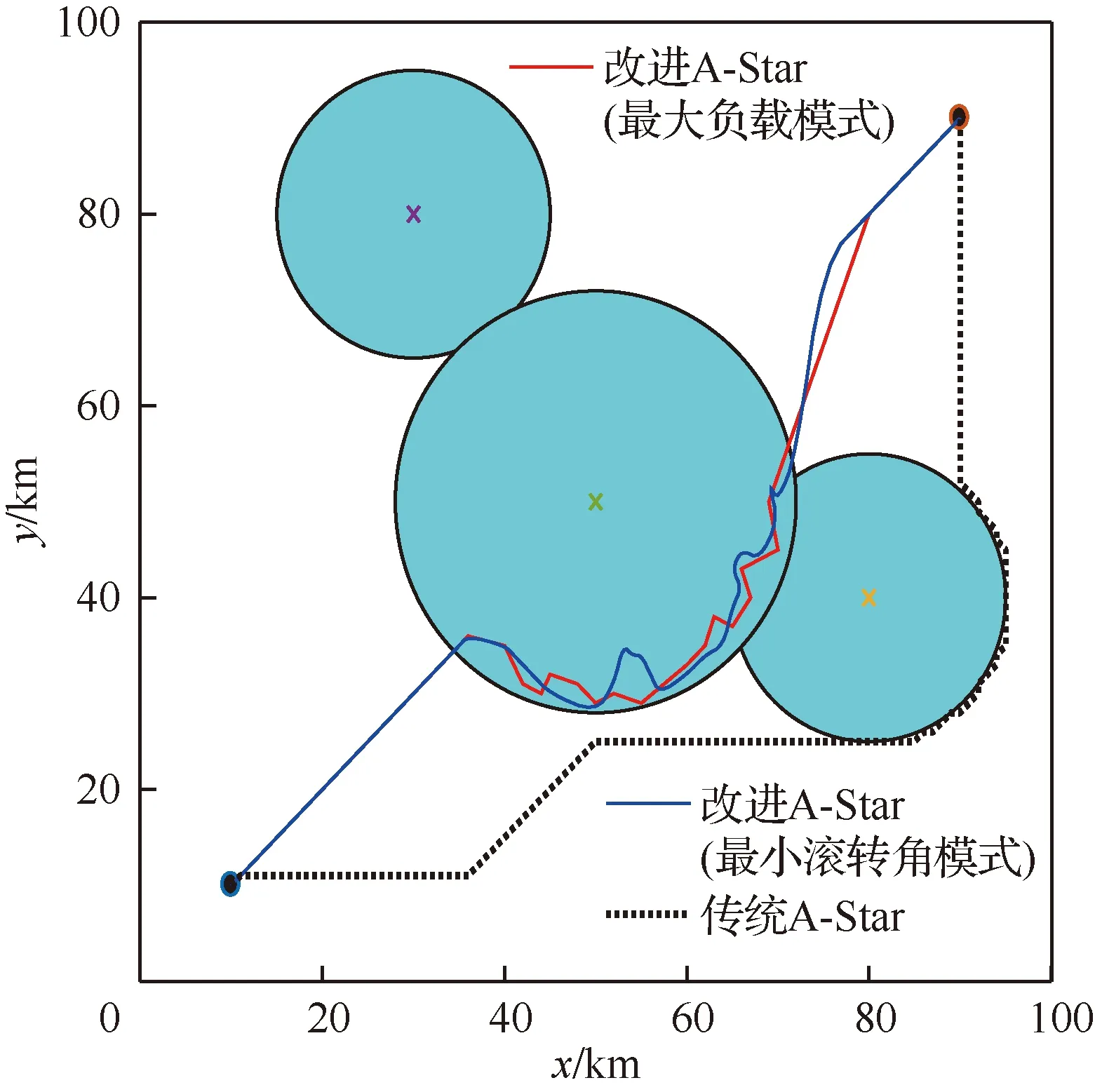
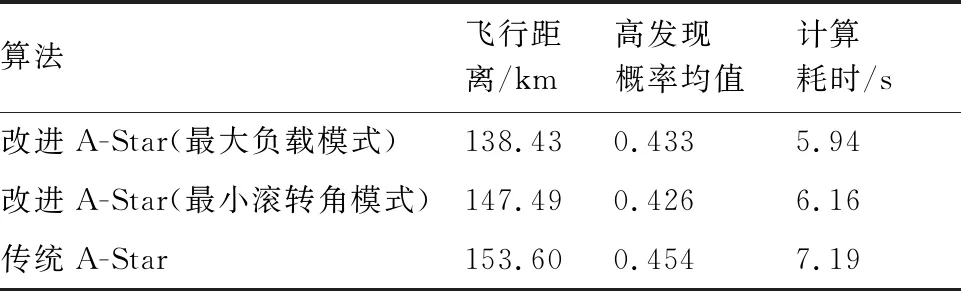
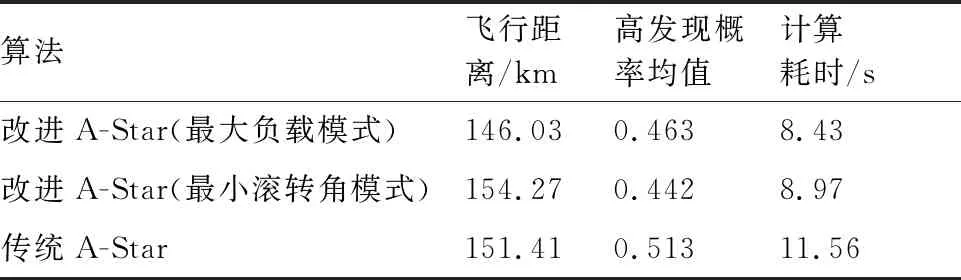
3.2 組網雷達系統
4 結 論

