基于FPGA的倒立擺模糊PID控制器設計實現

鄭浩 汪正祥 張鳳登

摘要：在FPGA上設計部署模糊自適應PID算法，并針對典型的自動控制對象——直線倒立擺完成穩擺控制，以驗證該算法的硬件可實現性。在直線倒立擺模型基礎上，運用模糊控制理論對PID參數進行自適應整定，再根據模糊PID處理過程，結合離散PID算法，采用半查表加半計算方式，在Quartus II及Modelsim平臺上完成Verilog HDL的硬件編程設計與仿真。通過Simulink仿真比較可知，模糊自適應PID相對于經典PID控制的響應性能指標更優，最后基于EP4CE6E22C8N芯片，以較少的資源開銷實現了控制器設計。基于FPGA的模糊自適應PID控制器能夠充分利用該器件特性，凸顯模糊自適應PID算法優勢，實現對倒立擺的實時控制。

關鍵詞：FPGA;模糊PID控制;直線倒立擺

DOI：10.11907//rjdk.192050 開放科學（資源服務）標識碼（OSID）：

中圖分類號：TP319文獻標識碼：A 文章編號：1672-7800（2020）006-0130-06

0 引言

倒立擺裝置是控制理論研究中一種可靠的實驗驗證對象，直線型倒立擺一般由擺桿、電機以及角度傳感器等組成，被廣泛應用于科研及教學中，同時其系統模型與許多工業產品具有很大相似性。如今，智能控制理論快速發展，而倒立擺系統的不穩定、非線性、強耦合、多變量特點，使其成為新控制方法或理論的理想驗證對象。李悟早等，充分討論各種控制系統與模糊控制相結合的優點、缺點和適用范圍，指出不同控制理論結合程度尚淺，因而各種控制理論深度融合是控制理論的發展方向之一。模糊PID（Proportion-Integral-DiffCrential）控制是復合控制理論的代表之一，即將模糊理論應用于PID參數整定。將其它智能控制理論，如粒子群優化算法等與PID控制相結合展開探究，文獻實現了基于粒子群算法的倒立擺分數階PID參數優化，PID傳統整定方法有試湊法、齊格勒一尼科爾斯經驗法等;傳統PID控制已經得到廣泛應用，佟遠等使用MCU（Micro-Control Unit）完成PID雙閉環旋轉倒立擺設計，但對于一些復雜系統難以做到實時有效控制;盧雍卿等等也針對傳統PID控制，在FPGA上實現了在液浮陀螺回路中的應用;白瑞林等總結出智能控制策略實現有兩個顯著特點：一是實時信息處理量遠大于控制量，二是信息流往往具有實時并行性要求。而現場可編程邏輯門陣列（Field-Programmable Gate Array，FPGA）本質上屆于硬件數字邏輯電路，其一大設計特點就是“面積換取速度”，能夠以硬件的大量并行工作替代軟件的順序指令執行。王利等分析指出，以往模糊邏輯控制應用基本依靠數字計算機或微處理器的軟件計算模糊邏輯量，并通過查表完成邏輯推理。綜合得出，FPGA相對于MCU等馮.諾依曼一哈佛體系的串行時序指令處理器而言，更適合部署智能控制策略。劉剛等在運用FPGA完成模糊自整定PID設計時，采用聯合Matlab的離線計算在線查表設計方法;黃霞等同樣使用該方法，對誤差e和誤差變化率ec在論域中的所有可能組合，按照模糊規則離線計算得出修正參數并存儲到ROM中，再由查表方式進行解模糊化并輸出修正參數，但這種方法需要較大的存儲單元消耗。Boukhalfa等實現了模糊PID控制器在雙星電磁電機直接轉矩控制中的應用;Arulmozhiyal設計實現了基于FPGA的直流電動機模糊PID控制器。本文將模糊PID整定過程劃分成不同模塊，改進半查表加半計算使用策略，采用Verilog語言分別進行設計驗證，消耗的硬件資源較少，并進行了整體時序驗證仿真，最后基于EP4CE6E22C8N芯片搭配外圍電路，完成了硬件模糊PID控制板設計。

1 模糊自適應PID控制器設計

1.1 模糊自適應PID控制原理

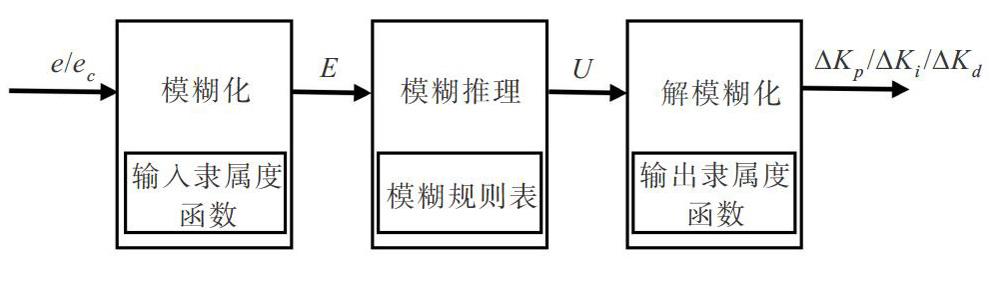
模糊自適應PID控制即將模糊理論與PID控制相結合，融合二者的原因主要是基于PID控制應用的廣泛性，使一些原本經典PID控制無法勝任的場合也能得以應用。PID參數模糊自適應方法，可以很好地彌補經典PID控制的不足。本質還是PID控制，只是使用了模糊化方法對PID參數作實時優化。單純的智能控制理論往往不具有確定性，經典或現代控制理論方法都須依靠精確的數學模型設計控制器，是確定的、收斂的設計方法。而模糊控制則是一種基于現實及經驗策略的控制方法，屬于智能控制理論，但需要在一定資源條件下才能夠獲得更出色的動態、靜態性能。模糊控制過程可按處理過程分為模糊量化處理，按模糊控制規則作模糊決策、非模糊化處理等環節。模糊PID控制中的關鍵就是PID參數的模糊控制輸出，因此將其分為輸入變量模糊化、隸屬值模糊推理、PID參數解模糊化3個階段，如圖l所示。

結合實際系統，首先將擺桿角度偏差及偏差變換率作為模糊輸入，對其模糊化得到輸入量的模糊子集，并計算其隸屬度，再利用模糊規則表進行模糊推理，即對模糊矩陣表作查表處理，得出輸出量的隸屬值，最后解模糊計算得到PID參數的修正值。利用Verilog進行硬件邏輯設計也是按照這一過程進行功能模塊劃分。

1.2 倒立擺系統控制結構

整個控制器仍是基于PID控制，控制器可以看作由模糊PID推理和PID控制器兩部分組成。控制器控制的對象就是直線一階倒立擺，倒立擺系統控制結構如圖2所示。

圖2中模糊PID控制器的設定參考輸入為θd，擺桿豎直為理想狀態，考慮到角度傳感器安裝位置，θd大小為270°。反饋輸入由倒立擺控制對象引出，即實時擺桿角度值θ。將二者之差作為系統誤差e，并得到誤差變化率ec（在離散情況下ec即當前誤差與上次誤差的差），最后將二者同時作為控制器的兩個輸入，根據離散PID公式得到控制輸出，以直流電機的PWM占空比為輸出，其中△Kp、△Ki、△Kd為模糊PID推理的輸出。

1.3 模糊自適應PID控制器設計

控制器為雙輸入單輸出，其中以擺桿角度與擺桿傾斜速度為輸入，以電機控制參數（直流電機轉速）為輸出。根據工程實踐，在此采用針對角度的閉環離散PID控制，為了平衡系統超調與響應速度，將初始PID值設為250、150、40，初始PID值選取對于倒立擺的最終性能有很大影響，也須通過反復實驗確定。最終PID參數為Kp=Kp0+△Kp、ki=Ki0+△Ki、Kd=Kd0+AKd。位置式離散PID如式（1）所示。

u（k）=kp·e（k）+ki·∑e（k）+Kd·ec（k） （1）

首先需要確定各輸人輸出量論域，文獻為了避免額外乘法操作消耗邏輯單元，將量化因子全部乘進論域中，在本文也是如此。其中，擺桿偏移角度范圍為[-20°，+20°]，選定輸入范圍既是下文系統模型線性化的要求，也是系統機械特性的實際要求，偏角過大時電機響應速度無法跟上。經過A/D轉換后e范圍為[-240，+240]，并設擺角偏差變化率ec的范圍為[-100，+100]、△Kp∈[-100，+100]、△Ki∈[-50，+50]、△Kd∈[-20，+20]。輸入輸出量均選擇同樣的模糊集{NB、NM、NS、ZO、PS、PM、PB}，分別代表負大、負中、負小、零、正小、正中、正大，將原始量按論域劃分后，分別對應到不同模糊子集，以少代多，就是模糊化的本質。對于計算隸屬度的隸屬函數，論域邊緣采用Z型和S型，其余采用線性的三角形隸屬函數。以輸入e為例，隸屬函數形式如圖3所示。

在模糊控制過程中模糊推理是核心，模糊推理規則表是基于PID的整定經驗而制定，PID各參數的作用可以簡單總結為：以比例控制為PID控制的基礎，即一般P是必需的，其與響應速度、超調均有關;積分控制I有助于減小穩態誤差，提高穩定性，但可能增加超調量;微分控制D可加大慣性系統響應速度并減弱超調趨勢，但與系統響應振蕩關系密切。據此制定△Kp、△Ki、△Kd的模糊規則表，以△Kp為例，其模糊推理規則如表1所示。

2 單級倒立擺系統建模仿真

2.1 倒立擺系統數學建模

將倒立擺系統抽象為小車、擺桿組成的系統。在不考慮摩擦阻力情況下，分析受力并將其線性化，系統狀態方程如下：

對式（3）進行拉氏變換并代人參數設定值，如表2所示，得到關于輸入量u和輸出角度量φ的傳遞函數。

2.2 控制系統Matlab仿真

首先在APP工具箱中找到Fuzzy Logic Designer，然后根據輸入輸出模糊子集新建模糊變量，再根據模糊規則表新建Rules，最后設置模糊推理采用Mamdani型，解模糊采用重心法。之后在Simulink中搭建系統模型，如圖4所示。模糊自適應PID控制與常規PID控制階躍響應曲線如圖5所示，比較分析可以看出前者在超調量、響應時間等方面性能更優。

3 控制器在FPGA上的設計與實現

從FPGA應用頂層模塊設計角度切人，即Top_Down設計概念。按照PID參數的模糊控制輸出過程，使用Verilog HDL進行設計，同時利用Altera提供的免費IP核進行輔助設計。整個控制器內有誤差處理模塊、模糊處理模塊（內部例化8個ROM模塊）、PID運算控制模塊（內部例化1個電機信號轉換模塊）共3個大模塊。此外，還用了一個分頻模塊，用于提供全局需要的分頻時鐘，可以使用內部PLL完成。所有模塊設計都是在RTL級別。

3.1 擺角誤差處理模塊設計

該模塊輸入為12位的A/D采樣值，已知在豎直位置處A/D值為ANGLE_MIDDLE=12'd3115。經過該模塊處理，輸出9位有符號的oute和outec，主要代碼如下所示。值得注意的是，Verilog中對于負數采取保存其補碼形式。通過仿真驗證，得到仿真時序圖如圖6所示。

3.2 模糊處理模塊設計

該模塊是整個設計的核心，可分成模糊化塊語句、模糊推理塊、解模糊塊語句。在模糊推理塊中采用查表方式進行模糊推理，而在解模糊塊語句中采用實時計算方式，也即使用半查表加半計算方式。對e模糊化主要代碼如下所示，對ec處理類似。

上述代碼的作用是對輸入的數字量進行模糊化處理，即按照上文中的模糊論域劃分，映射到對應的模糊子集。模糊推理塊主要語句如下所示，主要作用是先計算關聯模糊子集的隸屬度。為了避免小數運算的產生，在此過程中均先作整數化處理，再生成查詢儲存在ROM中模糊規則表的行列坐標，并從ROM塊中取出關聯的模糊子集值。

進行解模糊計算并輸出△Kp、△Ki、△Kd，再與初始設定的PID值相加。通過仿真驗證，得到仿真時序圖如圖7所示。

3.3 PID運算控制模塊設計

此目標控制的是直流電機，使用PWM的占空比變化控制電機轉速。PID運算控制模塊主要有計算電機轉速值，以及PWM波發生模塊。文獻提供了一種根據輸入脈沖頻率生成特定PWM波的方式;Sabri等提出根據某特定輸入量產生修正的輸出占空比可調的PWM方法，說明在實際中使用PD控制已足夠。通過仿真驗證，得到仿真時序圖如圖8所示。

3.4 控制系統硬件設計

整個系統硬件以Ahera的EP4CE6E22C8N芯片為核心，其最小工作電路一般包括調試口、外圍FLASH等，該FPGA芯片完全滿足此次設計要求。外圍電路包括電源電路、A/D轉換電路、電機隔離驅動電路等。系統硬件設計如圖9所示。

4 結語

本文采用一種半查表加半計算方式，基于Verilog語言進行倒立擺模糊PID控制器設計。對內部邏輯單位僅使用893/12060（7%），對內存bits的使用僅為3616/239616（2%），說明該設計具有經濟性。不足之處在于，系統初始參數選擇缺少方法總結，給運用帶來一定不便，并且未針對更高階倒立擺進行硬件設計，系統控制變量較少，無法完全突出模糊PID的優勢。因此，未來可以結合模糊自適應PID控制，仍以FPGA為控制核心，運用于其它更復雜高階倒立擺系統中。同時，該設計方法具有通用性，未來可方便用于其它控制場合。