一種基于BP神經網絡的鐵路大宗貨物運價風險預警判定方法

曾 進，郭少媛，戚芳榕，潘紅芹，董寶田

（1.北京交通大學 綜交通運輸大數據應用技術交通運輸行業重點實驗室，北京 100044；2.中國鐵路信息科技集團有限公司 信息工程管理部，北京 100844）

隨著運輸市場的競爭愈加激烈，鐵路貨物運輸的發展受到多方制約，為了獲取更大的市場份額和利潤，需要對貨物運價做出實時的風險預警。已有眾多學者對該領域進行了研究。魏方[1]研究干散貨遠洋運價市場波動風險評估，提出長記憶性波動風險評估、極端性波動風險評估、相關性波動風險評估系統方法。錢芳[2]闡述了中國航運市場運價預警機制的框架，并在研究支持向量機模型的基礎上，建立中國航運市場運價預警模型架構。朱玉華[3]運用ARIMA 模型分析了我國出口集裝箱運價指數的變動趨勢，并依據金融風險預警理論,建立了我國出口集裝箱運價風險預警機制模型。孫祖妮[4]分析我國鐵路運輸成本的構成及影響因素，以某鐵路運輸企業貨運成本預測為例，分別用成本動因神經網絡預測方法和灰色系統預測方法進行預測。張鎖[5]通過以定量分析為主、結合定性分析的方法,建立了基于VaR-GARCH 的風險度量模型,對市場風險進行研究。曹雪玲[6]等人通過分析鐵路危險貨物運輸風險因素，構建鐵路危險貨物運輸風險評價指標體系并應用模糊綜合評價法對鐵路危險貨物運輸風險進行評價。張光宇等人[7]進行了鐵路貨運價格管理系統的設計與開發，為做出合理的運價風險預警提供了參考。

以上風險預警方法均采用各指標的歷史數據，因其不能準確反映未來情況，使預警效果較易產生大的偏差。Bowersox 和Donald.J[8]帶領的研究小組于1999 年應用神經網絡算法進行物流成本研究，對宏觀物流成本進行估算。2003 年，Bowersox 小組再次采用人工神經網絡，以2000 年的數據為標準估算國家物流成本[9]。2005 年，Alexandre M.等人[10]建立了6 層人工神經網絡模型。使用神經網絡算法既考慮了歷史數據，又利用到實時數據，使得輸出的數據與期望值更為近似。BP 神經網絡是應用最廣泛的神經網絡之一，但目前還較少有使用BP 神經網絡算法對鐵路運價進行風險預警的實例。

1 基于BP神經網絡算法的鐵路運價風險預警模型

1.1 模型構建

本文選用典型的3 層BP 神經網絡結構模型，對大宗貨物鐵路運輸價格的風險進行預警。圖1 為該模型的拓撲結構。

圖1 BP神經網絡拓撲結構

圖中，xi(i=1,2,…,n)表示輸入數據；yj(j=1,2,…,m)表示輸出數據。

（1）確定輸入節點數

基于BP 神經網絡算法的鐵路運價風險預警模型的輸入應該為能全面描述鐵路運價風險的影響指標，這些指標來自于宏觀經濟、運輸市場、貨主與鐵路企業4 個方面。

（2）確定輸出節點數

輸出節點的個數對應需要進行風險預警的指標個數。在鐵路價格預警中，輸出節點個數為1。

（3）確定隱含層節點數

王選院士鉆研創新的科研精神深深影響著他的學子，本次尋訪的主角肖建國便是其得意的門生之一。在王選院士的指導和自身的不懈努力下，肖建國在計算機技術、圖像影像處理、網絡信息處理和排版印刷領域都取得了重大成就，推動了中國印刷技術的發展。同時圣為人師，培育英才，讓研究精神和技術與時俱進，代代相傳。

關于隱含層節點數的確定問題，實踐中常用經驗公式來取值，計算公式為：

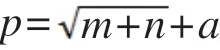
其中，p為隱含層節點個數；m為輸出層節點個數；n為輸入層節點個數；a取1 ～10 之間任意一個常數，當根號內計算結果非整數時，采用四舍五入原則進行運算。

1.2 鐵路運價風險預警指標體系的建立

風險預警的主要目的是根據預警指標的變化情況，反映風險的等級，要實現鐵路運價風險的合理預警，選擇合理的指標十分關鍵。本文根據鐵路貨運運營的具體情況以及指標選取原則，從宏觀經濟、運輸市場、貨主和鐵路企業4 個方面選取了21 個預警指標，建立的風險預警指標體系如圖2 所示。

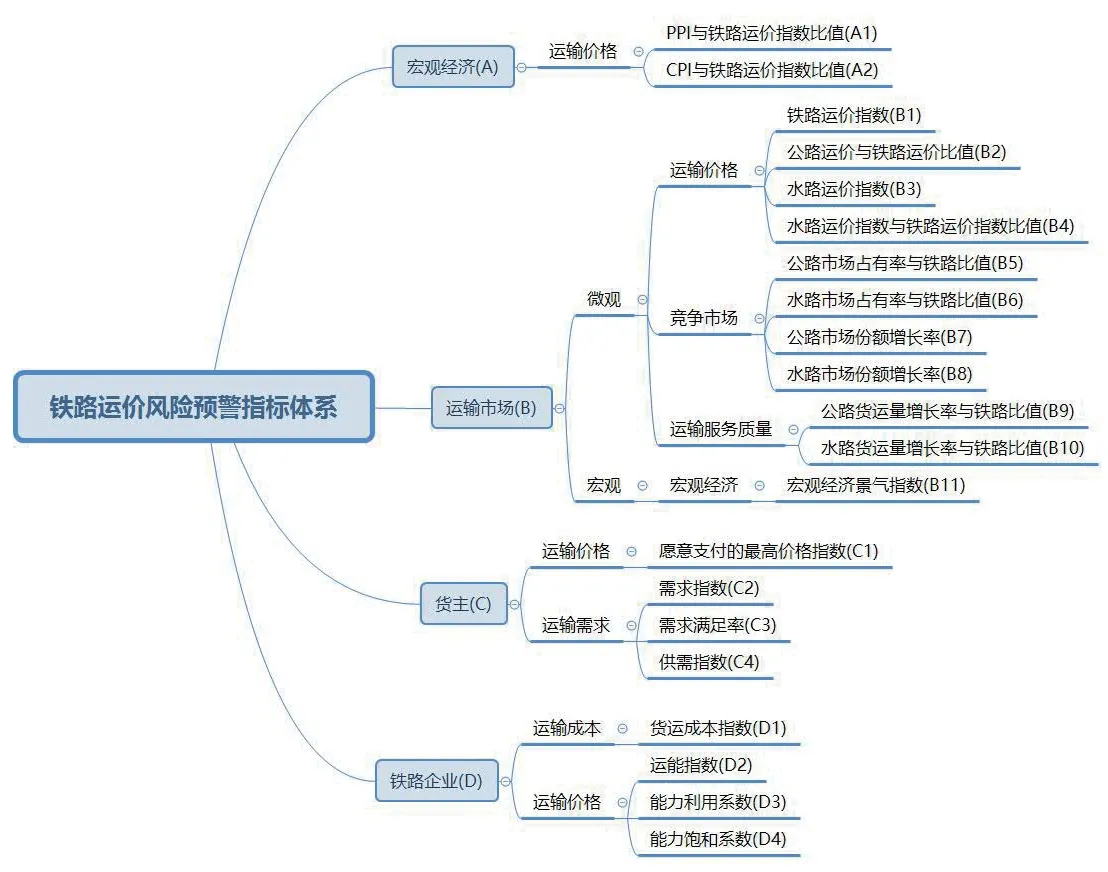
圖2 鐵路運價風險預警指標體系

圖中將21 個指標進行分類標號，與宏觀經濟相關的4 個指標為A 類，與運輸市場相關的11 個指標為B 類，與貨主相關的4 個指標為C 類，與鐵路企業相關的4 個指標為D 類，再逐一對每一類編號。

1.3 樣本數據歸一化

為了消除數據量綱的影響，BP 神經網絡的信息由輸入層向隱含層傳送時，需要使用轉換函數。為方便對輸入信號進行學習，將輸入信號進行收斂，本文選取S 型函數的正切形式tansig 函數作為隱含層節點和輸入層節點的激活函數；線性函數Purelin 的輸入值和輸出值可以取任意值，故此處選取線性函數Purelin 作為輸出層節點的轉換函數。

為滿足BP 神經網絡轉換函數對數據輸入的要求，本文采用Matlab 軟件對原始數據進行歸一化處理，采用的歸一化方法為（0，1）標準化法，計算公式為：

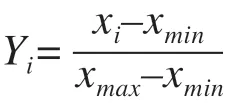
其中，Yi為數據i的歸一化結果；xi為數據i的實際值；xmin、xmax分別為該組數據的最小、最大值。

1.4 神經網絡訓練

圖3 BP神經網絡學習流程

2 案例分析

2.1 樣本數據的采集

鐵路大宗貨物運輸占全部品類運輸的70%以上，而其中煤炭類運輸又占到大宗貨物品類運輸的60%以上，本文選取煤炭的鐵路運輸做為案例的主要分析對象。在鐵路運輸的競爭者中，公路運輸最為主要，在800 km 以上的中長運輸距離中，鐵路的競爭優勢便開始體現，應該保證鐵路運輸在這部分市場占有較大的市場份額，故取800 km ～1500 km 中長距離運輸范圍進行模型驗證。

本文選取2015—2017 年影響鐵路運價的月度指標數據，每月數據為1 組，共36 組，作為原始樣本數據。隨機選取其中的27 組作為訓練數據，剩余9組作為驗證數據。本文對互聯網上可獲取的資料進行挖掘與整合，采用了來源于國家統計局、國家發改委、中國統計年鑒、中國鐵道年鑒及鄂爾多斯煤炭網等的相關數據，涉及宏觀經濟數據、鐵路貨運情況數據、公路運價指數及各種車型的公路平均運價等指標。

2.2 預警級別的確定與劃分

在預測出未來的鐵路運價預警指數之后，判斷運價的變動是否存在風險，若存在風險需要進一步劃分預警級別，使管理人員可根據預警級別制定相應措施。

對所選取的各組指標數據劃分預警級別，需先確定各組風險預警的綜合預警指數。綜合考慮煤炭各月的公鐵運價比值和運量比值雙項指標，來確定當月的經營效果。由于公路煤炭運量數據無法獲取，因此將運量比這一指標改為鐵路煤炭運量進行分析，而由于二者數量級相差較大，故在之后的分析中應先消除數量級的差異。當煤炭在該月的公鐵運價比值較低且運量數據也較低時，則需要進行風險預警。根據上述分析，將以上2 指標消除數量級差異后的比值作為綜合預警指數，劃分風險預警范圍，得出各組數據的預警級別如表1 所示。

本文預警級別的劃分標準為：

（1）若綜合預警指數在[0，0.71）范圍內，則鐵路運輸價格預警級別為正常（綠色）；

（2）若綜合預警指數在[0.71，0.90）范圍內，則鐵路運輸價格預警級別為藍色風險預警；

（3）若綜合預警指數在[0.90，1.00）范圍內，則鐵路運輸價格預警級別為黃色風險預警；

（4）若綜合預警指數在[1.00，1.10）范圍內，則鐵路運輸價格預警級別為橙色風險預警；

（5）若綜合預警指數≥1.10，則鐵路運輸價格預警級別為紅色風險預警。

2.3 模型運行情況與結果分析

2.3.1 隱含層節點個數的確定

本文建立的BP 神經網絡模型的輸入層節點個數為21，輸出層節點個數 為1。 由經驗公式可以確定隱含層節點個數應該在6 ～15 之間，需要經過多次訓練確定隱含層節點具體個數，并在訓練過程中計算不同網絡節點數的訓練誤差。隱含層的激活函數采用tansig 函數。

對網絡進行訓練，當網絡滿足設定的期望誤差或達到最大訓練步數時，訓練結束，可得到不同隱含層神經元個數對應的訓練所得誤差，如表2 所示。通過比較可以發現隱含層節點個數為13時，網絡的訓練誤差最小，所以選定隱含層節點的個數為13 個。

表1 鐵路運價預警級別劃分

表2 不同節點個數對應的誤差值

2.3.2 模型訓練與結果分析

隨機選取27 組樣本數據對基于BP 神經網絡的鐵路運價預警模型進行訓練，設學習速率為0.05，由圖4可知,在1 427次迭代后，訓練誤差逐漸趨于0。

由表3 可知，模型訓練的結果與實際值十分接近。

圖4 鐵路運價預警模型誤差訓練曲線

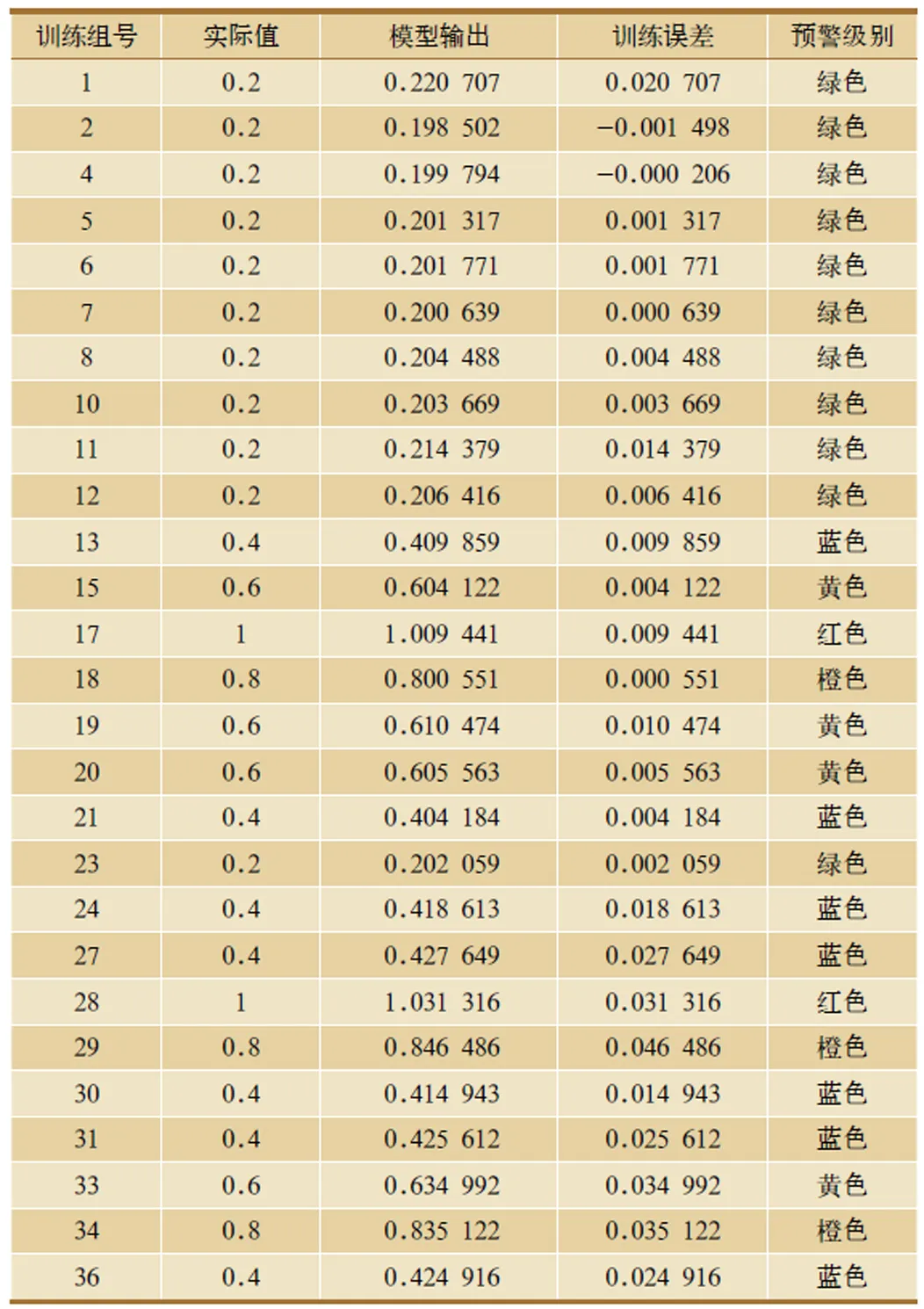
表3 鐵路運價風險預警模型訓練結果

以其余9 組樣本的數據為輸入數據，輸入以上建立的鐵路運價風險預警模型進行驗證，結果如表4 所示。

從表4 可以看出，隨機選取的9 組數據的模型輸出值與實際值十分接近，誤差較小，風險發生預警級別與實際相同。因此可以證明本文建立的神經網絡模型符合要求，可以用于鐵路運價的風險預警。

表4 鐵路運價風險預警模型檢驗結果

3 結束語

本文通過建立鐵路運價風險預警模型，驗證了基于BP 神經網絡算法進行鐵路運價風險預警的可行性，并且為其他領域風險預警模型的建立提供了參考。通過建立鐵路運價風險預警模型，可以有效地對鐵路運價進行合理調控，為鐵路運輸部門在貨運管理和貨運成本控制等領域提供準確及時的信息，豐富鐵路運輸企業的運價管理手段。