基于AGA?GRNN的三維室內定位研究

馬翠紅 徐天天 楊友良

摘? 要： 針對傳統的測距定位模型容易受到外部因素的干擾，故而降低了定位精度的問題，提出自適應遺傳算法廣義傳播神經網絡模型（AGA?GRNN）。引入自適應遺傳算法（AGA）用于優化廣義回歸神經網絡（GRNN）的參數，通過AGA?GRNN構建無線信號強度（RSSI）與目標位置之間的關系進行定位，利用對應的映射關系判斷目標位置。仿真結果表明，該算法在15 m×15 m×5 m范圍內的平均定位誤差為26.2 cm。 與GRNN及BP相比，計算精度分別提高了45.4%和53.6% 。同時將AGA優化GRNN三維定位模型與GA優化GRNN三維定位模型的優化時間進行了比較，結果表明，AGA?GRNN的平均定位時間減少了0.5 s，有效地提高了三維定位的精度和效率。

關鍵詞： 三維定位模型; 室內定位; AGA?GRNN; 射頻識別; 目標位置; 仿真實驗

中圖分類號： TN976?34; TP391.9? ? ? ? ? ? ? ? ?文獻標識碼： A? ? ? ? ? ? ? ? ? ? ? 文章編號： 1004?373X（2020）14?0090?04

Research on 3D indoor positioning based on AGA?GRNN

MA Cuihong， XU Tiantian， YANG Youliang

（North China University of Science and Technology， Tangshan 063210， China）

Abstract： In allusion to the traditional ranging and positioning model is easy to be disturbed by the external factors， which reduce the positional accuracy， an adaptive genetic algorithm generalized propagation neural network model （AGA?GRNN） is proposed. The adaptive genetic algorithm （AGA） is introduced to optimize the parameters of generalized propagation neural network （GRNN）， and the relationship between received signal strength indicator （RSSI） and target location is established with AGA?GRNN to conduct the positioning. The target position is judged by means of the corresponding mapping relation. The simulation results show that the algorithm′s average positioning error in the range of 15 m×15 m×5 m is 26.2 cm. In comparison with GRNN and BP， the calculation accuracy of this algorithm is increased by 45.4% and 53.6%， respectively. The lengths of optimizing time of the GRNN 3D positioning models optimized with AGA and GA are compared. The results show that the average positioning time of AGA?GRNN is reduced by 0.5 s， which effectively improves the accuracy and efficiency of 3D positioning.

Keywords： 3D positioning model; indoor positioning; AGA?GRNN; radio frequency identification; target location; simulation experiment

0? 引? 言

當今社會，三維室內定位技術在倉庫管理、醫療衛生等眾多方面中得到了大量應用。利用射頻識別（RFID）技術[1?2]標簽和讀取器兩者之間的接收信號強度（RSSI）來反映目標的空間信息，進而確定目標位置。 由于傳統測距方法易被外因因素所干擾而影響定位結果，因此為了改進測距定位算法的缺點，許多研究人員使用具有較好的非線性逼近能力的神經網絡定位方法，能較好地解決接收信號強度與目標物體位置間的非線性問題，從而得到了廣泛使用。BP神經網絡不僅參數較多，優化過程繁瑣，而且需要人為不斷調試，最終才能得到較為準確的三維室內定位模型，加大了構建預測模型的難度和計算成本[3] 。故選用自適應遺傳算法廣義回歸神經網絡定位模型（AGA?GRNN）來完成三維室內定位。與BP神經網絡不同，廣義回歸神經網絡（GRNN）[4?6]算法不需要人工確定網絡參數，在很大程度上避免了主觀設置對結果的影響。遺傳算法（GA） [7?10]的特點是不易陷入局部最優、易于同其他技術聯合使用。但固定的交叉變異概率使尋優效率較低，不易用于實時三維定位，故引入自適應遺傳算法（AGA）[11?12]。AGA通過個體適應度值而自適應調整交叉、變異概率，以提高算法的效率。通過使用AGA優化GRNN定位算法的參數，使三維室內定位算法的定位精度及效率得以提升。

1? AGA?GRNN三維定位模型構建

通過自適應遺傳算法（AGA）改進模型參數，使基于廣義回歸神經網絡的三維定位模型的定位精度和效率得以提高。GRNN善于處理不穩定的數據，適合解決非線性問題，并且當樣本數據較小時可以更好地對其進行預測。其中，高斯函數的寬度系數[σ]是GRNN網絡模型的參數又稱為光滑因子，常采用交叉驗證法得到一個最優值，但是耗時長、精度低。 因此本文使用AGA來優化網絡的光滑因子。傳統遺傳算法[7]具有易于與其他技術混合、群體搜索性強、無需輔助信息、不易陷入局部最優解等特點。然而，固定交叉和變異概率影響了遺傳算法的優化效率。因此，引入AGA算法依據個體的適應性對交叉和變異概率進行自適應調整，使計算效率得以提高。

1.1? GRNN模型

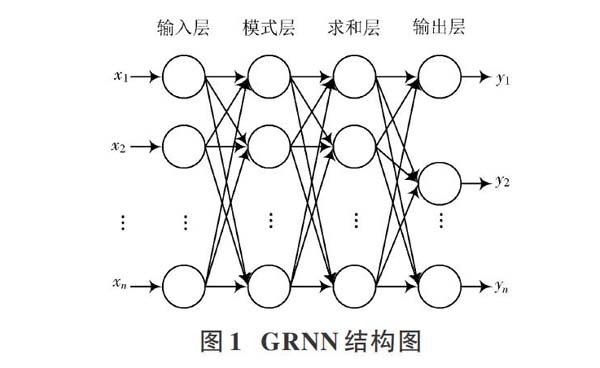
GRNN模型如圖1所示，由輸入層、模式層、求和層和輸出層四個部分構成。

GRNN網絡模型的輸入向量表示為[RSSI=[RSSI1，RSSI2，…，RSSIm]]，輸出向量表示為[Y=y1，y2，…，yn] 。

模型根據樣本集預測概率密度函數[f（RSSI，Y）]：

[f（RSSI，Y）=1（2π）（m+1）/2σ（m+1）·1ni=1nexp-（RSSI-RSSIi）T（RSSI-RSSIi）2σ2·exp-（Y-Yi）22σ2]? ?（1）

式中：指定模型參數[σ]的樣本概率密度函數用[f（RSSI，Y）]表示;模型輸入層的維數用[m]表示; [n]為樣本個數;樣本概率寬度用[σ]表示，即模型參數;第[i]個輸入向量用[RSSIi]表示;第[i]個輸出向量用[Yi]表示。

GRNN定位模型具有高度通用性的原因在于概率密度函數是從樣本集中導出的。同時，GRNN定位模型不僅有良好的容錯性，而且在定位過程中能減少因RSSI值的波動對定位精度的影響，進而提高了網絡模型的定位能力。

在概率密度函數已知的情況下，實際測量的RSSI可根據式（2）預測出目標物體的真實位置。

[Y=E（YRSSI）? ? =i=1nYi·exp-（RSSI-RSSIi）T（RSSI-RSSIi）2σ21ni=1nexp-（RSSI-RSSIi）T（RSSI-RSSIi）2σ2] （2）

式中：實際測量的信號強度向量用RSSI表示;預測位置向量用Y表示。

GRNN網絡模型可以根據輸入和輸出自動調整，權重參數可以直接由樣本數據確定，避免了迭代訓練。 然而，在室內定位中，信號強度會被環境因素所影響，同一位置接收的 RSSI值會發生明顯的波動從而導致實時收集的樣本在訓練樣本中出現頻率較低。當參數[σ]過小時，會出現過擬合現象，導致定位結果出現明顯變化; 當參數[σ]過大時，會使預測精度降低。因此，選擇適當的參數[σ]至關重要。

1.2? AGA?GRNN三維定位模型

通過AGA改進GRNN網絡的光滑因子，從而構建AGA?GRNN三維定位模型。

1） 初始化遺傳算法，在光滑因子的取值范圍中，可隨機產生規模為 NIND的初始種群，通過實數編碼，得出最大遺傳代數及遺傳算法選擇概率等參數，進化代數。

2） 通過建立與遺傳算法相適應的函數，使用近似函數計算GRNN算法的輸出結果與真實值坐標之間的誤差的平方和并取其倒數，該值可以評估種群中個體的適應度函數，通常該值越小，說明個體越差，反之該值越大，表明個體越優良。適應度函數為：

[fit=1i=1n（Yi-Yi）2] （3）

式中：[Y]和[Y]分別表示訓練數據對應的真實值和輸出值;n為輸入數據的數目。

3） 選擇。根據個體適應度選擇初始種群，保留第一個個體的概率，公式如下：

[Pj=fitjm=1NINDfitm]? ? ? ? ? ?（4）

4） 交叉、變異：保留的個體用于交叉和變異的算法。通過在交叉、變異概率的選擇中引入自適應確定機制，使其隨著個體適應值的改變而自適應的變化，其調整公式為：

[Pc=k1fmax-f′fmax-favg，? ? ? ? ?f′≥favgk3，? ? ? ? ? ? ? ? ? ? ? ? ? f′≤favg]? ? ? （5）

[Pm=k2fmax-ffmax-favg，? ? ? ? ? ? f≥favgk4，? ? ? ? ? ? ? ? ? ? ? ? ? ? ?f≤favg]? ? （6）

式中：[f]為變異的父個體適應值;[fmax]為種群個體的最大適應值;[f′]為要交叉的個體中較大的適應度值;[favg]為種群的平均適應值;固定參數k1=0.5，k2=0.02，k3=0.85，k4=0.05。最后得到新的種群，進化代數。

5） 確定進化代數g是否達到最優值，如果達到，則停止運算并回到具有最高適應度的個體; 否則再次對步驟2）進行運算。

6） 利用最優平滑因子值作為GRNN網絡模型的參數，建立三維室內定位模型。

7） 計算預測結果，評估AGA?GRNN網絡性能。

2? 仿真實驗

為了檢驗AGA?GRNN三維定位算法的定位效果，將該算法同BP定位算法和GRNN定位算法進行對比。通過計算機仿真在Matlab環境中收集三維室內定位的輸入輸出、運行時間、參數變化等數據，并對三種三維室內定位算法的定位效果進行測試。考慮到真實環境中地面位置人流量大、物品較多的問題，本文將閱讀器放在房頂的四個角上，在Matlab的仿真實驗中閱讀器的位置坐標如圖2閱讀器布置圖所示，分別為（0，0，5），

（0，15，5），（15，0，5），（15，15，5）。

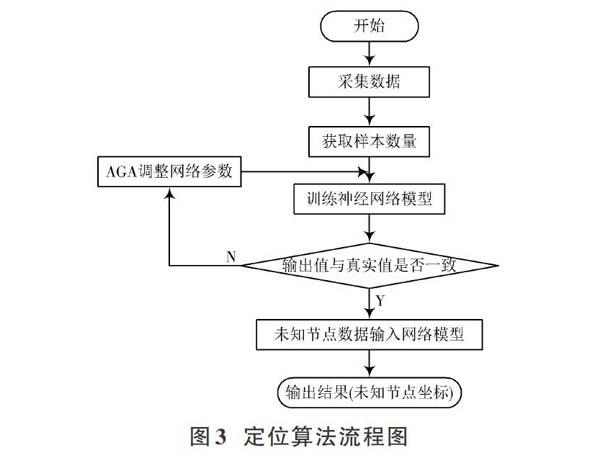
將閱讀器讀取的信號強度值（RSSI）作為 AGA? GRNN定位模型的輸入，把參考標簽的三維坐標作為輸出，并且訓練 AGA? GRNN三維室內定位模型。用50組數據樣本進行30次迭代對定位模型進行訓練， 然后使用9組標簽進行定位測試，以確定測試獲得的定位坐標是否與真實坐標相匹配。 定位算法流程圖見圖3。

3? 結果分析

3.1? 定位精度比較

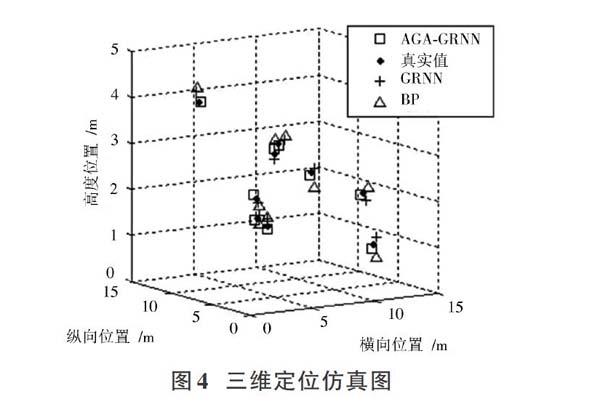
三維定位的仿真結果如圖4所示。其中，目標物體的真實坐標用實心點表示;AGA?GRNN算法定位坐標用方塊表示;GRNN定位算法坐標用加號表示;BP定位算法坐標用上三角表示。

如圖5定位誤差所示，將AGA?GRNN三維定位算法與BP定位算法、GRNN定位算法通過定位結果的距離誤差進行比較。 BP定位模型的最大定位誤差與最小定位誤差分別為68 cm和45 cm。GRNN定位模型的最大定位誤差與最小定位誤差分別為56 cm和37 cm。而AGA定位模型的最大定位誤差與最小定位誤差分別為33 cm和17 cm，實際坐標和預測坐標誤差在35 cm以內。可以看出，AGA?GRNN與BP定位方法、GRNN定位方法相比，定位精確度明顯提高。

3.2? 光滑因子優化效率分析

將 AGA與 GA優化效率進行了對比，運用 AGA算法優化光滑因子時，初始種群規模為30，進化代數為50，選擇概率為0.9，按照種群適應度值自適應調整交叉和變異概率，光滑因子取值范圍為（0，50）。同時，將AGA算法與 GA算法優化光滑因子效率進行對比， AGA算法的光滑因子優化運行時間為2.2 s，GA算法的光滑因子優化運行時間為2.7 s，優化時間提高了0.5 s，可見 AGA算法在優化光滑因子時效率顯著提高。

4? 結? 語

本文提出一種自適應遺傳算法來優化廣義回歸神經網絡的三維室內定位模型。運用大量數據對AGA?GRNN定位模型進行訓練，同時通過9組數據對定位模型進行測試。通過仿真實驗取得了不錯的定位效果，仿真結果證明，三維室內定位模型 AGA? GRNN在參數優化定位效率上高于 GA?GRNN，同時比 BP，GRNN具有更高的定位預測精度，節約成本的同時又降低了計算量， 具有較好的應用前景。

注：本文通訊作者為徐天天。

參考文獻

[1] 趙凱，胡海峰.神經網絡和RFID相融合的室內定位算法[J].激光雜志，2015，36（8）：138?141.

[2] 吳超，張磊，張琨.基于BP神經網絡的RFID室內定位算法研究[J].計算機仿真，2015，32（7）：323?326.

[3] HAO Linzhe， WEN Xianbin， LI Dan. Amorphous location algorithm based on BP artificial neural network [C]// International Conference on Frontiers of Things. [S.l.]： IEEE， 2014： 13?23.

[4] LI Erchao， MA Yuquan. The application of improved adaptive genetic algorithm in the optimization of discrete variables [J]. Journal of discrete mathematical sciences and cryptography， 2018， 21（2）： 417?421.

[5] BENDU H， DEEPAK B B V L， MURUGAN S. Multi?objective optimization of ethanol fuelled HCCI engine performance using hybrid GRNN?PSO [J]. Applied energy， 2017， 187： 601?611.

[6] 文萌，錢晨，黃丹.基于BFA?GRNN的飛行績效預測[J].電光與控制，2018，25（4）：78?82.

[7] 楊曉吟.基于蟻群優化遺傳算法的智能自動組卷算法研究[J].現代電子技術，2018，41（21）：121?123.

[8] KUMAR S， KUMAR N， LIU S F. An inventory model for deteriorating items under inflation and permissible delay in payments by genetic algorithm [J]. Cogent business & management， 2016， 3（1）： 161?172.

[9] 孔國立，張璐璐.遺傳算法的廣義回歸神經網絡建模方法[J].計算機工程與設計，2017，38（2）：488?493.

[10] SAMATTAPAPONG Nara， AFZULPURKAR Nitin. A production throughput forecasting system in an automated hard disk drive test operation using GRNN [J]. Journal of industrial engineering and management， 2016， 9（2）： 330?358.

[11] BAO Beifang， YANG Yu， LIU Aijun， et al. Task allocation optimization in collaborative customized product development based on adaptive genetic algorithm [J]. Journal of intelligent systems， 2014， 23（1）： 1?19.

[12] 余發山，高勇.基于AGA優化RBF神經網絡的礦井通風機故障診斷[J].電子測量技術，2017，40（9）：241?245.

[13] 林悅，夏厚培.交叉驗證的GRNN神經網絡雷達目標識別方法研究[J].現代防御技術，2018，46（4）：113?119.