變剛度電液力系統(tǒng)主導(dǎo)極點(diǎn)模型自適應(yīng)控制研究*

李朝朝，金曉宏,*，王 坤，張紹峰

(1.武漢科技大學(xué) 冶金裝備及其控制教育部重點(diǎn)實(shí)驗室，湖北 武漢 430081；2.武漢科技大學(xué) 機(jī)械傳動與制造工程湖北省重點(diǎn)實(shí)驗室，湖北 武漢 430081)

0 引 言

位置擾動型被動式電液力系統(tǒng)(以下簡稱“電液力系統(tǒng)”)是一種根據(jù)被加載對象位移要求準(zhǔn)確地施加期望力，同時該位移又對自身加載產(chǎn)生擾動的電液力系統(tǒng)，具有控制精度高、響應(yīng)速度快、承載能力強(qiáng)等優(yōu)點(diǎn)[1]。電液力系統(tǒng)是一個復(fù)雜的非線性系統(tǒng)，當(dāng)負(fù)載剛度變化較大時，系統(tǒng)的控制品質(zhì)和穩(wěn)定性會受到明顯影響[2]。如何在變負(fù)載剛度情況下提升電液力系統(tǒng)的加載特性顯得尤為重要。

模型參考自適應(yīng)控制(model reference adaptive control，MRAC)是一種通過設(shè)計理想?yún)⒖寄Ｐ停米赃m應(yīng)機(jī)構(gòu)，使實(shí)際系統(tǒng)快速、準(zhǔn)確、穩(wěn)定地向理想?yún)⒖寄Ｐ褪諗康目刂扑惴ǎ軌蛴行б种葡到y(tǒng)非線性、參數(shù)時變帶來的不確定性影響[3]。由于該算法不需要在線辨識，較常規(guī)控制算法還提高了系統(tǒng)的響應(yīng)速度，被廣泛應(yīng)用于控制系統(tǒng)中。如ZHAO Yi-fei等[4]采用MRAC實(shí)現(xiàn)了對電液伺服系統(tǒng)的高精度位置控制；蘇士杰等[5]在電液伺服試驗機(jī)主動加載條件下通過MRAC提高了力系統(tǒng)的控制品質(zhì)。

本文采用MRAC方法，以電液力系統(tǒng)為研究對象，首先探討負(fù)載剛度變化對系統(tǒng)的影響，并根據(jù)系統(tǒng)理想模型設(shè)計出一種基于主導(dǎo)極點(diǎn)，且滿足嚴(yán)格正實(shí)、穩(wěn)定最小相位系統(tǒng)要求的三階等效參考模型，通過模型自適應(yīng)控制器使電液力系統(tǒng)穩(wěn)定地跟蹤理想?yún)⒖寄Ｐ停云谝种曝?fù)載剛度變化對系統(tǒng)的影響，從而提高系統(tǒng)響應(yīng)特性和控制精度。

1 系統(tǒng)組成及工作原理

電液力系統(tǒng)原理圖如圖1所示。

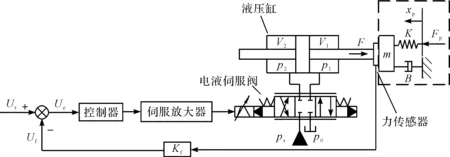
圖1 電液力系統(tǒng)原理圖

圖1中，將被加載對象簡化為一個彈簧阻尼系統(tǒng)(虛線框所示)。系統(tǒng)根據(jù)與被加載對象位移相關(guān)的力發(fā)生函數(shù)發(fā)送指令信號Ur到控制器，通過電液伺服閥在液壓缸兩腔產(chǎn)生壓力差PL(PL=P1-P2)，活塞桿在PL作用下，輸出力F=PLA(A—活塞桿有效面積)作用于被加載對象并由力傳感器檢測，力傳感器將測得的力信號反饋給輸入端，實(shí)現(xiàn)閉環(huán)控制。

2 數(shù)學(xué)模型

根據(jù)文獻(xiàn)[6]電液力系統(tǒng)中各環(huán)節(jié)數(shù)學(xué)方程，以力F為輸出，以電液伺服閥閥芯位移Xv和被加載對象位移XP為輸入，可得輸出力F的拉氏域表達(dá)式如下：

(1)

式中：M=mVt/(4Ee)；N=BVt/(4Ee)+mKc；Z=BKce+KVt/(4Ee)+A2；J=KKce；Vt—液壓缸總空腔容積，m3；Ee—油液彈性模量，Pa；Kce—總流量-壓力系數(shù)，(m3/s)/Pa；m—負(fù)載等效質(zhì)量，kg；Kq—閥口流量增益，(m3/s)/Pa；B—運(yùn)動部件黏性阻尼系數(shù)，N/(m·s-1)；K—電液力系統(tǒng)負(fù)載剛度，由負(fù)載彈性剛度、活塞桿剛度和力傳感器連接剛度3部分組成，N/m。

(2)

式中：ω0—負(fù)載固有頻率，ω0=(K/m)1/2；ζ0—負(fù)載阻尼比，ζ0=B/[2(Km)1/2]；ω1—負(fù)載剛度與液壓彈簧并聯(lián)偶合的剛度與負(fù)載質(zhì)量形成的綜合固有頻率，ω1=ω0(1+Kh/K)1/2；ζ1—阻尼比，ζ1=2EeKce/[ω0Vt(1+K/Kh)]；ω2—負(fù)載剛度與液壓彈簧串聯(lián)偶合的剛度與阻尼系數(shù)之比，ω2=(KceKKh)/[A2(K+Kh)]。

由式(2)可知，電液力系統(tǒng)的3個轉(zhuǎn)折頻率ω0、ω1和ω2均與參數(shù)K、Kh和m有關(guān)，當(dāng)負(fù)載質(zhì)量m和液壓彈簧剛度Kh一定時，電液力系統(tǒng)的系統(tǒng)特性主要取決于負(fù)載剛度K。

下面筆者以一具體電液力系統(tǒng)，進(jìn)行系統(tǒng)特性分析，研究不同負(fù)載剛度對系統(tǒng)性能的影響。

電液力系統(tǒng)參數(shù)如表1[8]所示。

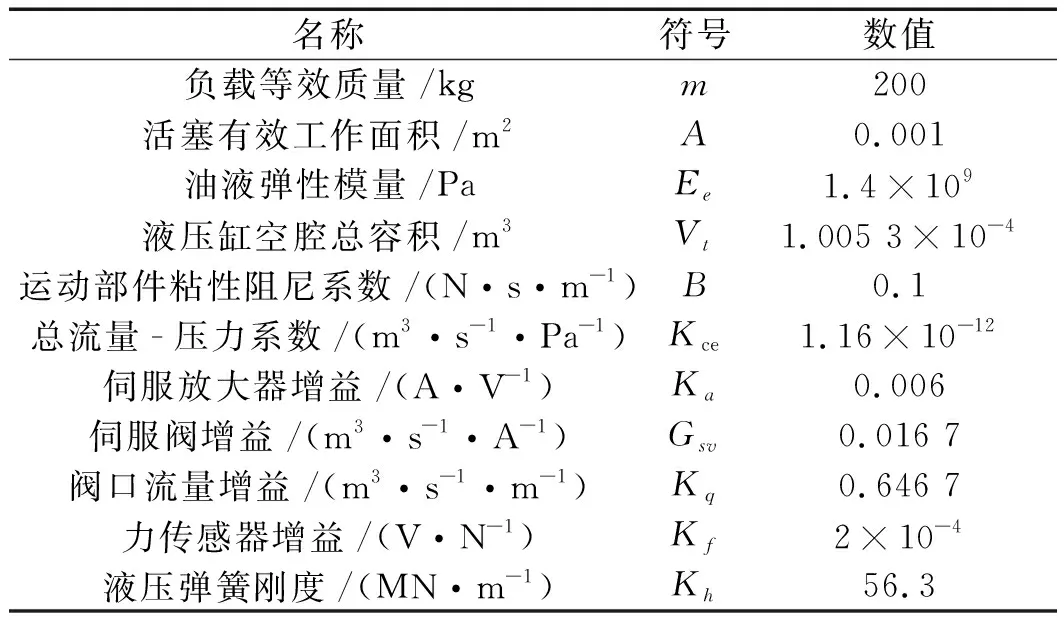
表1 電液力系統(tǒng)參數(shù)表

電液力系統(tǒng)所模擬的彈性負(fù)載剛度為變剛度，用來模擬大型閥門開度控制中負(fù)載剛度的變化。

筆者對系統(tǒng)輸入幅值為2 kN的階躍指令信號，分別取K為1 MN/m、5 MN/m、13 MN/m、25 MN/m、35 MN/m、50 MN/m進(jìn)行仿真實(shí)驗，得到不同負(fù)載剛度下電液力系統(tǒng)階躍響應(yīng)曲線如圖2所示。

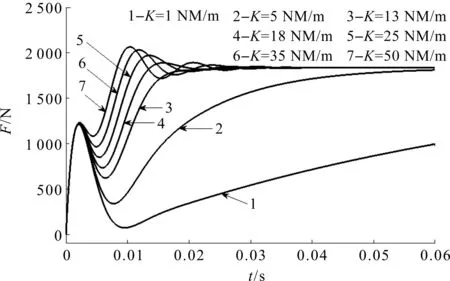
圖2 不同負(fù)載剛度下電液力系統(tǒng)階躍響應(yīng)曲線

圖2中，曲線均在2 ms內(nèi)從0 N迅速上升至1 224 N，然后開始下降，負(fù)載剛度越小，下降幅度越大，持續(xù)時間越長，當(dāng)K=1 MN/m時，曲線于9.5 ms才下降到其最低點(diǎn)(9.5，72.9)。曲線經(jīng)歷下降段后開始二次上升，當(dāng)K=1 MN/m～13 MN/m時，K越大，系統(tǒng)上升速度越快，調(diào)整時間越短；當(dāng)K=13 MN/m～50 MN/m時，系統(tǒng)在保持原有上升規(guī)律基礎(chǔ)上出現(xiàn)超調(diào)現(xiàn)象，K越大，其最大超調(diào)量越大，系統(tǒng)調(diào)整時間越短。最終不同剛度下的系統(tǒng)輸出力達(dá)到相同穩(wěn)態(tài)值1 836 N，穩(wěn)態(tài)精度為91.8%。

3 基于主導(dǎo)極點(diǎn)的MRAC策略

針對電液力系統(tǒng)中負(fù)載剛度變化會導(dǎo)致系統(tǒng)不穩(wěn)定、控制精度差等問題，本研究提出采用MRAC策略。通過將參考模型的理想輸出ym與電液力系統(tǒng)的實(shí)際輸出yp作差，得到實(shí)時廣義輸出誤差e(t)，自適應(yīng)機(jī)構(gòu)通過實(shí)時調(diào)整控制器參數(shù)使e(t)趨向于0，使得電液力系統(tǒng)輸出向參考模型輸出靠近并最終達(dá)到一致[9]。

3.1 基于主導(dǎo)極點(diǎn)的參考模型設(shè)計

參考模型的選取直接決定了電液力系統(tǒng)的控制效果。主導(dǎo)極點(diǎn)作為一種將高階系統(tǒng)簡化為低階系統(tǒng)來做定量估算的方法，系統(tǒng)特性主要由主導(dǎo)極點(diǎn)決定。

由式(2)知電液力系統(tǒng)是由一階慣性環(huán)節(jié)、二階振蕩環(huán)節(jié)和二階微分環(huán)節(jié)組成的三階系統(tǒng)，故筆者采用以主導(dǎo)極點(diǎn)標(biāo)準(zhǔn)化傳遞函數(shù)為基礎(chǔ)，構(gòu)造出分子分母階數(shù)與實(shí)際系統(tǒng)傳遞函數(shù)結(jié)構(gòu)形式一致、可以獨(dú)立進(jìn)行調(diào)整的三階參考模型，其形式為：

(3)

筆者將二階振蕩環(huán)節(jié)的一對共軛復(fù)數(shù)極點(diǎn)作為主導(dǎo)極點(diǎn)，通過恰當(dāng)?shù)嘏渲闷渌麡O點(diǎn)使其對整個系統(tǒng)的影響忽略不計，即三階參考模型的特性主要由二階振蕩環(huán)節(jié)的固有頻率ωn和阻尼比ζ決定。

根據(jù)系統(tǒng)性能指標(biāo)，筆者選取電液力系統(tǒng)的液壓固有頻率作為參考模型固有頻率，從表1參數(shù)計算得系統(tǒng)液壓固有頻率為529.15 rad/s，取ωn=530 rad/s。由系統(tǒng)最大超調(diào)量Mp≤10%確定二階振蕩環(huán)節(jié)最佳阻尼比ζ=0.707。故二階振蕩環(huán)節(jié)的一對共軛復(fù)數(shù)極點(diǎn)為：

(4)

在控制理論中，其他極點(diǎn)實(shí)部的值是主導(dǎo)極點(diǎn)實(shí)部值的5倍以上[10]。基于該條件確定參考模型中一階慣性環(huán)節(jié)1/(Ts+1)的極點(diǎn)為：

s3=-10ζωn=-3 747.1

(5)

將式(4，5)代入式(3)，得到參考模型傳遞函數(shù)基本形式如下：

(6)

式中：b0=1.053×109；b1=3.089×106；b2=4 496.52。

在MRAC控制器中，參考模型Gm(s)需滿足嚴(yán)格正實(shí)、穩(wěn)定最小相位系統(tǒng)條件，此時式(6)需滿足下列不等式：

(7)

根據(jù)式(6，7)，選取a=2 000，Km=263.25，得到基于主導(dǎo)極點(diǎn)的參考模型傳遞函數(shù)為:

(8)

本研究對參考模型進(jìn)行仿真計算，得到參考模型單位階躍響應(yīng)中的上升時間為3.76 ms，最大超調(diào)量為4.69%，響應(yīng)達(dá)到穩(wěn)態(tài)值±2%時所對應(yīng)的調(diào)整時間為10.5 ms。

由伯德圖可知，-10°相移頻率為88.89 rad/s，根據(jù)雙十標(biāo)準(zhǔn)[11-13]計算得參考模型頻寬為14.1 Hz，故所選取的參考模型頻寬較寬、動態(tài)響應(yīng)性好，滿足系統(tǒng)性能要求。

3.2 模型參考自適應(yīng)控制器設(shè)計

本研究根據(jù)Narendra穩(wěn)定自適應(yīng)控制器方案[14]設(shè)計自適應(yīng)控制器，由式(2)可知電液力系統(tǒng)傳遞函數(shù)的分母、分子分別為3階和2階，配置可調(diào)增益Kc和兩個反饋信號補(bǔ)償器F1和F2共同組成自適應(yīng)控制器。

模型參考自適應(yīng)控制框圖如圖3所示。

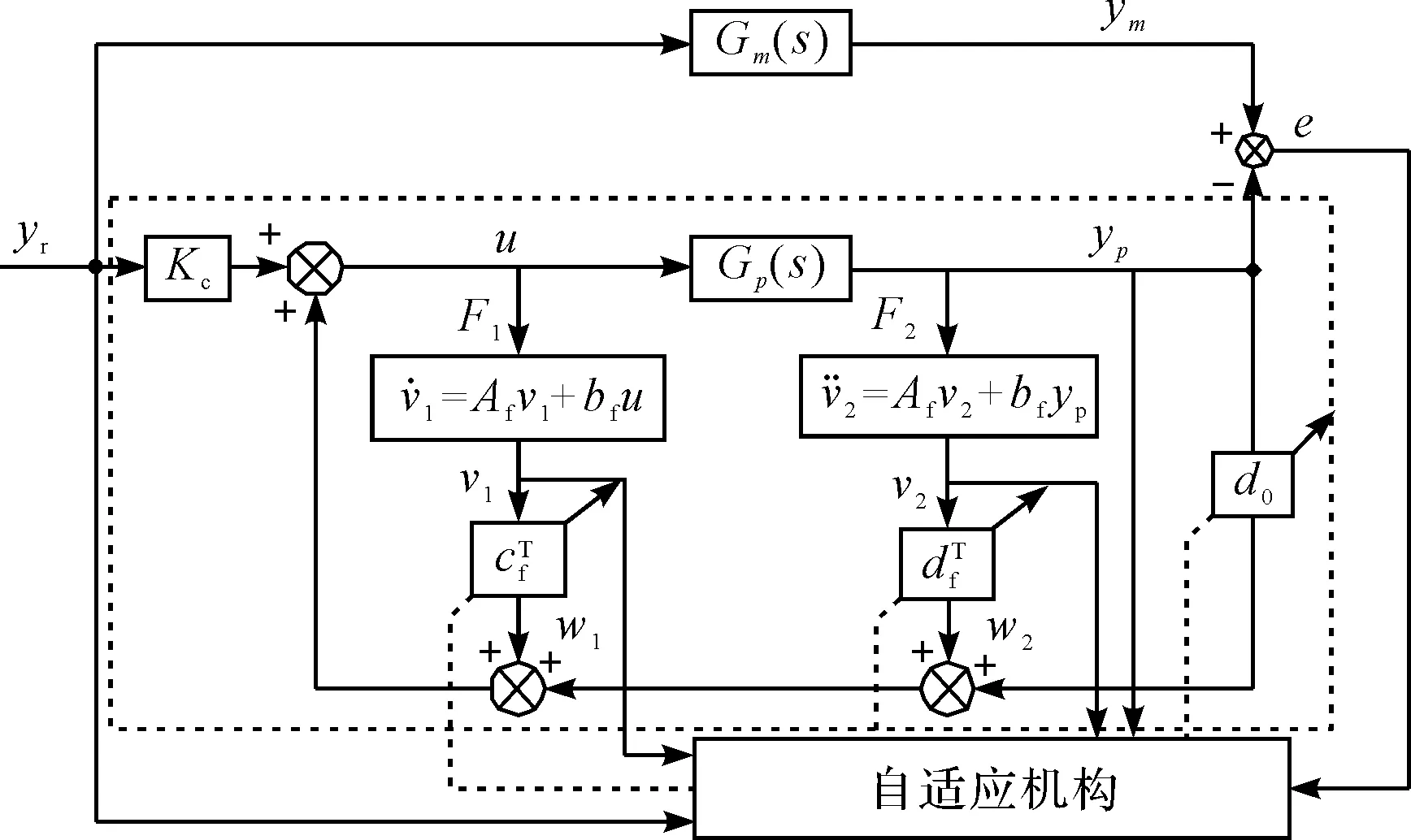
圖3 模型參考自適應(yīng)控制框圖

電液力系統(tǒng)的狀態(tài)方程及傳遞函數(shù)為：

(9)

式中：xp—3維狀態(tài)向量；u—控制量；yp—電液力系統(tǒng)輸出量；Ap—3×3維狀態(tài)矩陣；bp，h—3×1維向量；Kp—電液力系統(tǒng)增益，Kp>0；Np(s)，Dp(s)—2階和3階首一多項式，且Np(s)為Hurwitz多項式。

主導(dǎo)極點(diǎn)模型的狀態(tài)方程及傳遞函數(shù)為：

(10)

式中：xm—3維狀態(tài)向量；yr—模型輸入；ym—模型輸出；Am—3×3維矩陣；bm—3×1維向量；km—模型系統(tǒng)增益；Nm(s)，Dm(s)—2階和3階首一多項式。

兩個反饋信號補(bǔ)償器的狀態(tài)方程及傳遞函數(shù)分別為：

(11)

(12)

式中：v1，v2—2維列向量；Df(s)—2階首一Hurwitz多項式；Nc(s)，Nd(s)—1階多項式。

即：

(13)

式中：Af—待選2×2漸近穩(wěn)定矩陣；cf，df—2維列向量。

即：

(14)

選擇Df(s)=Nm(s)，并構(gòu)造兩反饋信號補(bǔ)償器狀態(tài)方程：

(15)

電液力系統(tǒng)GP(s)、可調(diào)增益Kc、兩個反饋信號補(bǔ)償器F1和F2共同組成了自適應(yīng)力系統(tǒng)，自適應(yīng)控制律u為：

(16)

式中：θT(t)—可調(diào)參數(shù)向量，θT(t)=[Kc(t)cfT(t)d0

(t)dfT(t)]；φ(t)—信號向量，φ(t)=[yr(t)v1T(t)yP

(t)v2T(t)]。

可調(diào)參數(shù)自適應(yīng)律為：

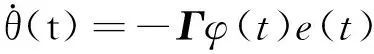
(17)

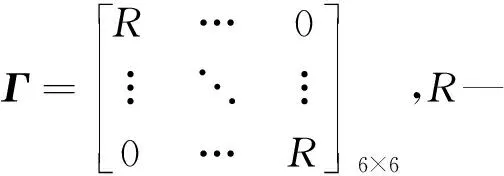
根據(jù)Lyapunov穩(wěn)定性理論，式(17)表示的自適應(yīng)控制律能保證系統(tǒng)全局漸進(jìn)穩(wěn)定。

4 仿真分析

為驗證基于主導(dǎo)極點(diǎn)模型自適應(yīng)控制算法的有效性，本研究在Matlab/Simulink中建立電液力系統(tǒng)數(shù)學(xué)模型，使用表1參數(shù)進(jìn)行仿真，采用ode23算法，設(shè)置最大步長為1×10-5s、計算相對誤差為10-6。

4.1 不同自適應(yīng)系數(shù)，自適應(yīng)力系統(tǒng)跟蹤參考模型效果

負(fù)載剛度K=50 MN/m，本研究對自適應(yīng)力系統(tǒng)輸入幅值為3 kN的階躍指令信號。參照文獻(xiàn)[15]的方法，自適應(yīng)系數(shù)R分別取為100、5 000、50 000、100 000，得到不同R時自適應(yīng)力系統(tǒng)階躍響應(yīng)跟蹤誤差指標(biāo)評價表，如表2所示。

表2 不同R時自適應(yīng)力系統(tǒng)階躍響應(yīng)跟蹤誤差指標(biāo)評價表

由表2可知，自適應(yīng)力系統(tǒng)能夠快速跟蹤參考模型并保持穩(wěn)定，隨著R的增大，系統(tǒng)跟蹤誤差最大值減小，誤差收斂時間變短。

當(dāng)R=100 000時，系統(tǒng)跟蹤誤差最大值僅為0.03 N，誤差收斂時間為0.8 ms，與R=50 000相比其跟蹤精度提升幅度已很低，故當(dāng)R>100 000時自適應(yīng)力系統(tǒng)跟蹤效果不會發(fā)生大幅度提升，后面仿真中均取R=100 000。

4.2 不同負(fù)載剛度，自適應(yīng)力系統(tǒng)指令跟蹤效果

本文對電液力系統(tǒng)輸入幅值為2 kN的階躍指令信號，取負(fù)載剛度K分別為1 MN/m、13 MN/m、50 MN/m，得到不同負(fù)載剛度下自適應(yīng)力系統(tǒng)階躍響應(yīng)曲線如圖4所示。

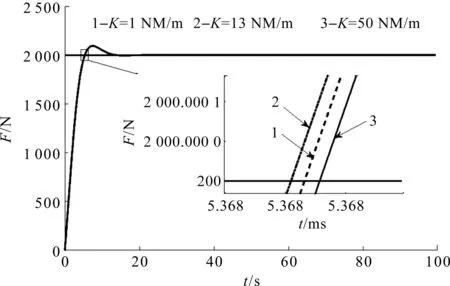
圖4 不同負(fù)載剛度下自適應(yīng)力系統(tǒng)階躍響應(yīng)曲線

筆者定義曲線的最終值作為系統(tǒng)響應(yīng)性能指標(biāo)中的穩(wěn)態(tài)輸出值，得到不同負(fù)載剛度下系統(tǒng)階躍響應(yīng)動態(tài)性能對比結(jié)果，如表3所示。

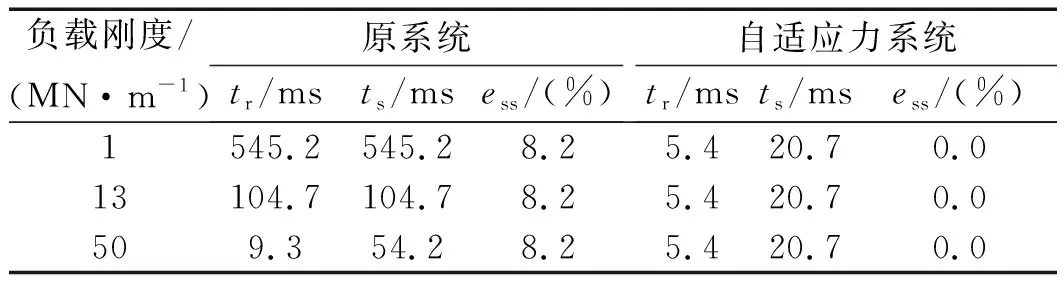
表3 不同負(fù)載剛度下系統(tǒng)階躍響應(yīng)動態(tài)性能對比

由表3可知：

原系統(tǒng)在3種負(fù)載剛度條件下的穩(wěn)態(tài)誤差均大于8%，控制精度較差；而自適應(yīng)力系統(tǒng)不同負(fù)載剛度下均能在20.7 ms內(nèi)快速跟蹤指令信號且具有極佳的一致性。

上述結(jié)果表明，基于主導(dǎo)極點(diǎn)模型自適應(yīng)控制器能夠抑制負(fù)載剛度變化對電液力系統(tǒng)的影響，消除系統(tǒng)在響應(yīng)過程中出現(xiàn)的波動現(xiàn)象，從而有效提高系統(tǒng)的控制精度和響應(yīng)速度。

4.3 不同頻率正弦指令，加入自適應(yīng)控制器前后對比

K=50 MN/m時，對原系統(tǒng)與自適應(yīng)力系統(tǒng)分別輸入3種不同頻率的正弦指令信號：F01=3+2.5sin10πt(kN)、F02=3+2.5sin20πt(kN)和F03=3+2.5sin28πt(kN)，得到不同頻率正弦指令下系統(tǒng)性能對比如表4所示。

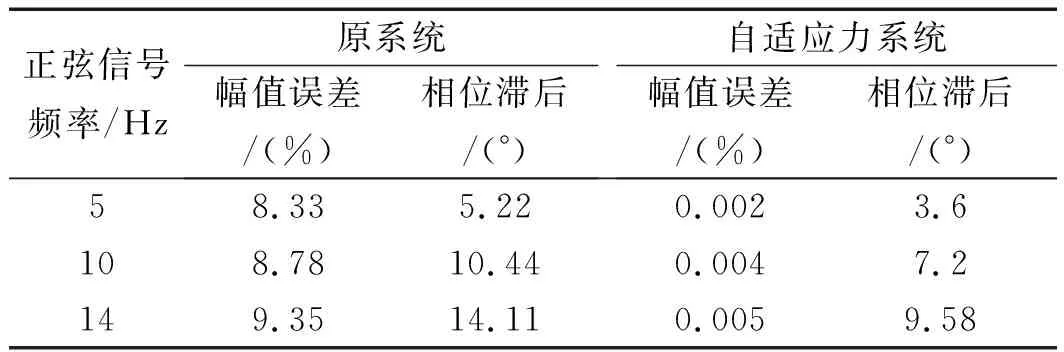
表4 不同頻率正弦指令下系統(tǒng)性能對比

其中，原系統(tǒng)和自適應(yīng)力系統(tǒng)14 Hz時正弦響應(yīng)曲線如圖5所示。

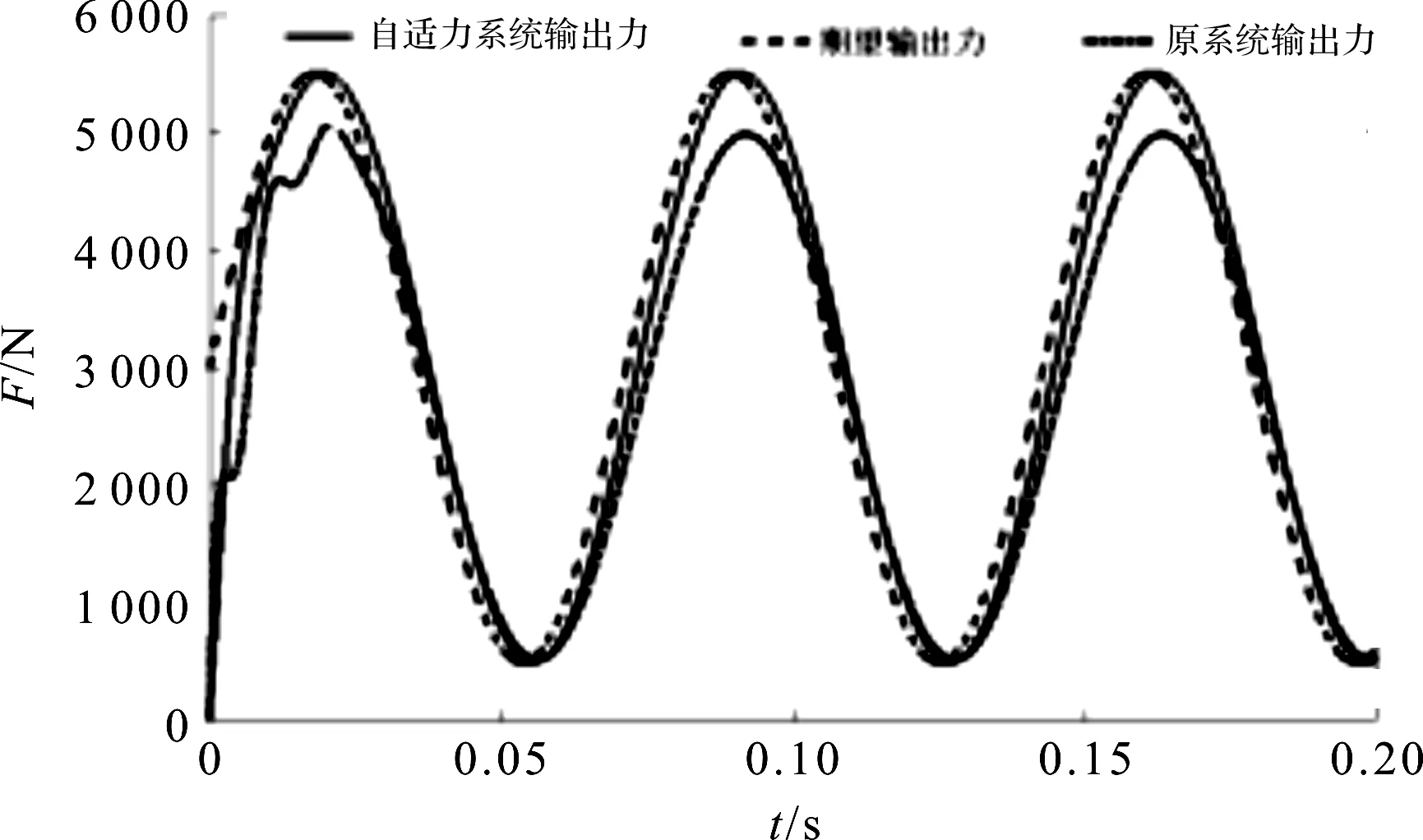
圖5 原系統(tǒng)和自適應(yīng)力系統(tǒng)14 Hz時正弦響應(yīng)曲線

由圖5可知：

原系統(tǒng)的輸入頻率從5 Hz上升至14 Hz時，其幅值誤差已由8.33%增長至9.35%；而自適應(yīng)力系統(tǒng)在14 Hz時幅值誤差僅為0.005%，相位滯后9.58°。

上述結(jié)果表明，自適應(yīng)力系統(tǒng)在14 Hz情況下依然能很好的跟蹤指令信號，并保持較高的控制精度。

4.4 位置擾動下，加入自適應(yīng)控制器前后對比

輸入幅值為2 kN的階躍指令信號，負(fù)載剛度K分別取為35 MN/m、50 MN/m，在0.1 s時對原系統(tǒng)和自適應(yīng)力系統(tǒng)分別加入0.005 m的階躍位置擾動xp，得到0.1 s時階躍位置擾動下系統(tǒng)響應(yīng)曲線如圖6所示。

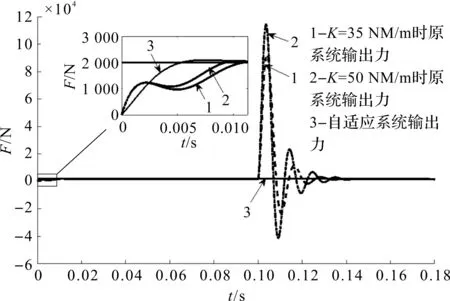
圖6 0.1 s時階躍位置擾動下系統(tǒng)響應(yīng)曲線

由圖6可知：

加入位置擾動后，原系統(tǒng)在K取35 MN/m和50 MN/m時對應(yīng)的最大誤差分別為92.8 kN和114.4 kN，并均于0.168 s再次達(dá)到穩(wěn)態(tài)值1 836 N。

自適應(yīng)控制器內(nèi)部自適應(yīng)參數(shù)Kc、d0的變化曲線如圖7所示。

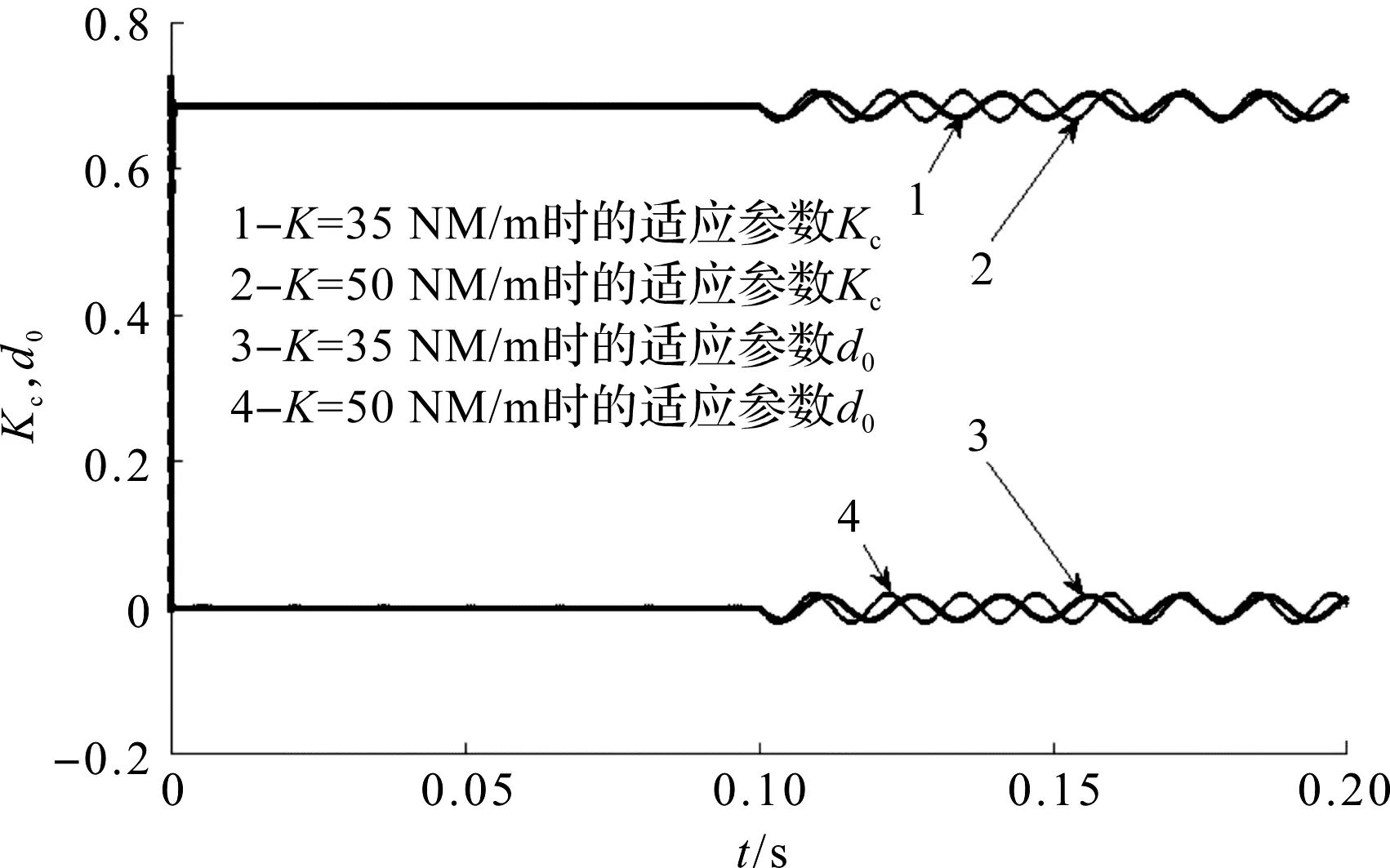
圖7 自適應(yīng)參數(shù)Kc、d0變化曲線

由圖7可知：

自適應(yīng)力系統(tǒng)通過快速調(diào)整控制器參數(shù)，有效抑制了位置干擾對系統(tǒng)控制精度和穩(wěn)定性的影響，使其穩(wěn)態(tài)誤差接近于0 N。

5 結(jié)束語

針對位置擾動型被動式電液力系統(tǒng)中負(fù)載剛度變化會導(dǎo)致系統(tǒng)不穩(wěn)定、控制精度差等問題，本研究設(shè)計了基于主導(dǎo)極點(diǎn)模型參考自適應(yīng)控制器，通過仿真分析可得到如下結(jié)論:

(1)電液力系統(tǒng)加入自適應(yīng)控制后，其跟蹤精度與自適應(yīng)系數(shù)R有關(guān)，R越大，系統(tǒng)跟蹤誤差越小，誤差收斂速度越快。當(dāng)R=100 000時，誤差最大值為0.03 N，誤差收斂時間為0.8 ms，系統(tǒng)能夠快速準(zhǔn)確的跟蹤參考模型；

(2)電液力系統(tǒng)響應(yīng)過程中的波動現(xiàn)象與負(fù)載剛度K有關(guān)，當(dāng)K>13 MN/m時，K越大，波動現(xiàn)象越劇烈。加入自適應(yīng)控制后，系統(tǒng)在20.7 ms內(nèi)快速跟蹤指令信號并消除波動現(xiàn)象，有效提高了系統(tǒng)的控制精度和響應(yīng)速度；

(3)電液力系統(tǒng)在5 Hz時響應(yīng)特性較差，加入自適應(yīng)控制后，系統(tǒng)在14 Hz情況下依然能很好的跟蹤指令信號，并保持較高的控制精度，有效拓展了系統(tǒng)頻寬；

(4)電液力系統(tǒng)受到位置干擾時，其輸出力短時間發(fā)生劇烈變化，控制精度受到嚴(yán)重影響，而加入自適應(yīng)控制后，位置干擾對系統(tǒng)影響極小，有效提高了系統(tǒng)的抗干擾能力。