基于線性自抗擾理論的三維吊車控制

摘要：針對吊車控制系統非線性、強耦合，欠驅動等特點。本文設計了線性自抗擾控制器解決這一問題。對比LQR控制效果，仿真和實驗結果表明本文所設計線性自抗擾控制具有較好的魯棒性、穩定性和較強的實時性。

關鍵詞：吊車;線性自抗擾控制;魯棒性;LQR控制

中圖分類號：TP391 ? 文獻標識碼：A ? ? 文章編號：1007-9416（2020）06-0000-00

橋式吊車作為一種大型的現代搬運工具，在建筑工程中廣泛使用。本文根據吊車擺動過程中存在控制時間長，擺角幅度大等問題。由于非線性自抗擾控制器[1]存在整定參數多，調參相對復雜，故使用線性自抗擾控制器，不僅控制效果佳且應用廣泛。

1 吊車試驗平臺數學模型

選擇某公司三維橋式吊車模型作為實驗對象。通過分析可得到系統的狀態方程。選擇x軸方向作為研究且其變量完全解耦，設，作為控制輸入，則狀態方程為：

上式1中為負載的質量，Mx為小車及導軌（沿x方向）質量，吊繩與z軸、xz平面的夾角，L為擺繩長度，為沿x方向的拉力，為沿x方向的摩擦力系數。

2設計線性自抗擾控制器

為了實現小車位置與擺角的參數整定，參照文獻[2]設計了線性自抗擾控制器，設二階被控對象的狀態方程為：

式（2）中，f（x1，x2）為系統的已知擾動部分，w（t）為未知擾動部分，b為放大系數，u（t）為系統控制量。二階線性ADRC系統中的跟蹤微分器（TD）：p0為輸入信號，p1，p2分別為p0的跟蹤信號和微分信號，用于跟蹤小車目標位置和參考位移，可調參數r決定跟蹤速度，越大，跟蹤速度越快。線性擴張觀測器（LESO）中的y（t）為系統輸出，當前變量的估計值Z1，

Z2分別為y（t）的跟蹤信號與微分信號，Z3為系統總擾動估計值，而Z3/b0構成反饋結構，用來補償擾動，e（t）為誤差信號，位置補償控制量u= u0- Z3/b，u0為吊車運行過程中r和φ的控制量。線性組合控制（LSEF）：， 其中、e1為誤差信號，、e2為微分信號;u0為虛擬控制量，u表示小車位置控制量。LSEF模塊將這些控制量重新組合生成新的控制量，并將其作為系統最終的控制輸入。

3 仿真實驗

在MATLAB的simulink環境下，搭建仿真框圖，其中擺線初始長度l0=56cm，質量Mx =6.157kg，摩擦系數Dx=20.37，行程為0.76m。控制器各部分參數跟蹤微分器：r1=40，r2=

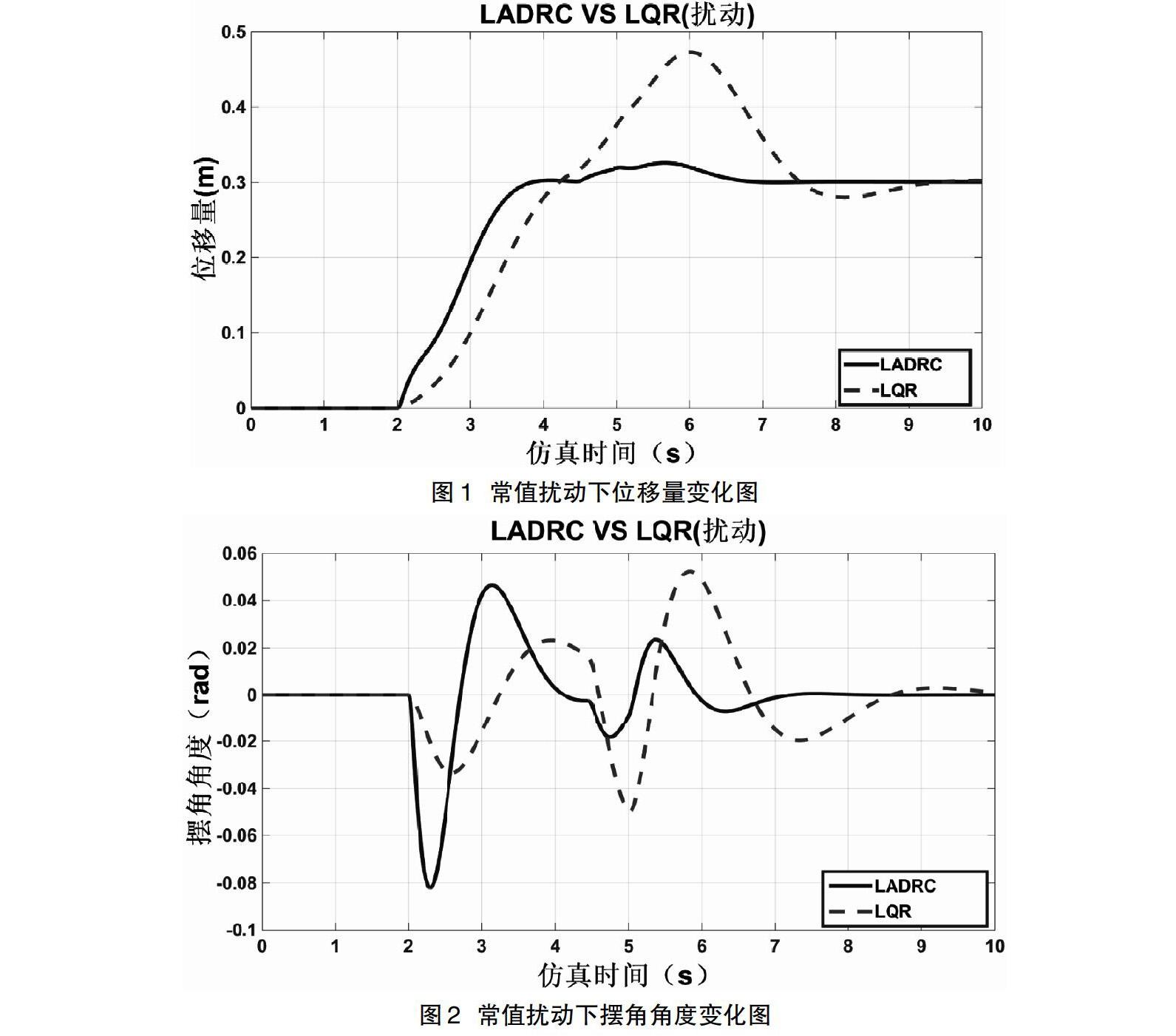
60，運用PID調整的經驗調整線性組合參數得出k1=8;k2=1.2;k3=0.003;k4=1，符號以構成負反饋為準;線性擴張觀測器參數b0=-2.2;wc=50，LQR[3]控制器參數為k1=2.0550;k2=2.3976;k3=-3.0392;k4=-3.1374，為了驗證控制器的魯棒性，給小車施加常值擾動，得到圖1位移變化圖、圖2擺角變化圖。

由圖1、圖2可以看出，LADRC和LQR雖然都有一定的抗擾動性能，但是LADRC在受到擾動時，能迅速地補償干擾信號，位移和角度曲線能迅速回到參考位移的指定位置，幾乎不受干擾信號影響，可見線性自抗擾控制器的抗干擾性能非常強，對工程具有實際指導意義。

4 結論

本文設計的線性自抗擾控制器，實現了三維吊車系統的解耦及調整控制，保證控制的實時性。通過仿真對比LQR控制，得出線性自抗擾控制器具有良好的效果，不僅能迅速消擺，還能在有干擾情況下，獲得良好的魯棒性。

參考文獻

[1] 韓京清.自抗擾控制器及其應用[J].控制與決策，1998（1）：19-23.

[2]武利強，韓京清.直線型倒立擺的自抗擾控制設計方案[J].控制理論與應用，2004，21（5）：665-669

[3] 宋玉琴，路彥剛，鄧思成，等.塔吊防擺LQR最優控制器研究[J].測控技術，2019，38（3）：131-134.

收稿日期：2020-04-20

作者簡介：鄧微（1987—），男，湖南新邵人，碩士，助教，從事鐵路噪聲預測及控制、智能優化的研究工作。