毫米波中繼網絡離散正交匹配追蹤混合預編碼算法

丁青鋒,高鑫鵬,鄧玉前

(華東交通大學 電氣與自動化工程學院,南昌 330013)

0 概述

隨著智能無線設備的不斷更新,人們對其傳輸速率的要求也越來越高[1]。大規模多輸入多輸出(Multiple-Input Multiple-Output,MIMO)中繼預編碼通信技術因其具有高波束增益[2],能夠補償毫米波信道傳輸中的路徑損耗,且擴大了通信范圍,已成為下一代移動通信的關鍵技術之一[3-4]。

當利用大規模天線陣列進行傳輸時,采用全數字預編碼結構具有高昂的射頻鏈成本[5]。因此,具有較少射頻鏈路的混合預編碼方案成為大規模MIMO中繼預編碼技術的研究熱點[6-7]。文獻[8]將傳統通信網絡中混合預編碼問題表述為空間稀疏重構問題,并提出空間稀疏預編碼算法,實現接近全數字預編碼的性能。針對部分連接結構的最佳混合預編碼問題,文獻[9]分析高信噪比和低信噪比下的優化方案,并采用注水算法實現最佳混合預編碼器。

相比于傳統通信,中繼通信在求解最優中繼混合預編碼矩陣時涉及多變量聯合優化,并且優化約束具有多個非凸條件,導致直接對中繼混合預編碼進行設計變得極其復雜。針對具有最小均方誤差的中繼混合預編碼系統,文獻[10]通過將六階聯合優化問題分解成3個二次約束二次優化的子問題,采用逐次逼近的迭代算法高度近似該問題,從而求得最優化混合預編碼矩陣。針對全雙工中繼混合預編碼系統,文獻[11]通過使用正交匹配追蹤理論對存在自干擾的混合預編碼矩陣進行干擾消除,并對能量效率與頻譜效率進行聯合優化分析。針對存在不完美信道狀態信息條件下的中繼混合預編碼設計問題,文獻[12]利用信道的長期特性,設計模擬波束形成矩陣,并推導得出可實現頻譜效率的分析界限。上述設計通常假設模擬預編碼器的相位是通過使用無限量化精度移相器產生的,但是現如今的技術無法實現過高量化精度移相器的設計[13],并且過高的量化精度需要高昂的硬件成本與功耗[14-15]。

針對中繼節點混合預編碼的多階非凸特性,為突破因采用過高量化精度移相器所帶來的系統硬件限制,本文提出一種基于有限量化精度移相器的中繼混合預編碼算法。該算法以最大化系統信息速率為目標,將中繼節點預編碼問題描述為空間稀疏重構問題,并利用離散化正交匹配混合預編碼算法進行求解。

1 系統模型

1.1 中繼大規模MIMO系統

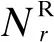
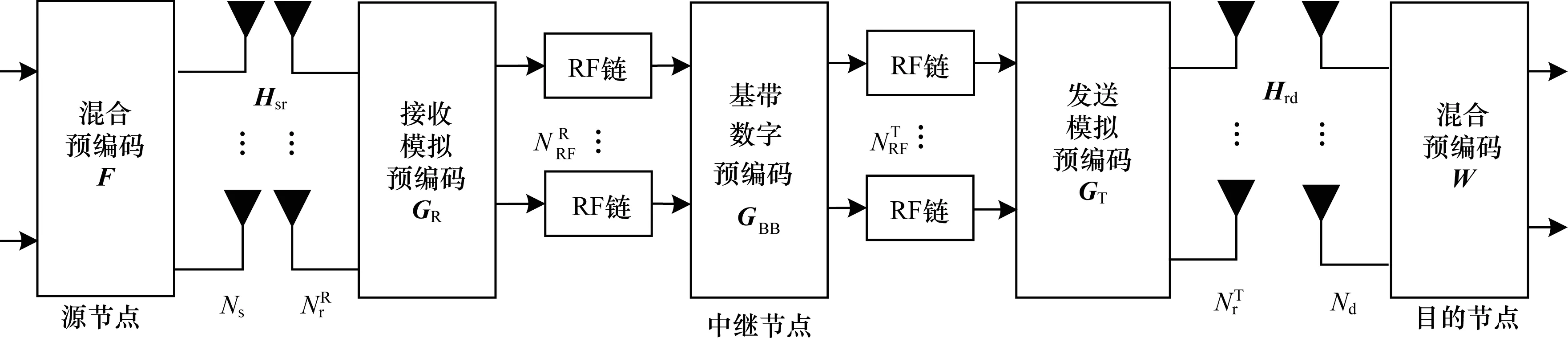
圖1 中繼節點混合預編碼模型

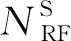
(1)

(2)

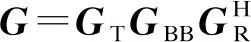
y=WHxd

(3)

1.2 毫米波信道模型

毫米波信道通常為集群信道,且具有可由低階矩陣表示的稀疏結構。本文采用Saleh-Valenzuela信道模型[16]來體現毫米波通信的信道特性。

源節點至中繼節點信道以及中繼節點至目的節點信道分別表示為:

(4)

(5)

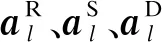
本文采用均勻平面天線陣列,水平方向具有間距為dx的N個天線,其陣列響應矢量表示為:

(6)

其中,λ為波長,ζ∈{S,R,D}為各節點集合。

垂直方向具有間距為dy的M個天線,其陣列響應矢量表示為:

(7)

其中,λ為波長,ζ∈{S,R,D}為各節點集合。

2 離散化中繼混合預編碼方案

2.1 混合預編碼矩陣求解

針對中繼混合預編碼問題,假設發送的信號滿足高斯分布,并且所有信道狀態信息均為已知。結合式(2)和式(3),毫米波中繼大規模MIMO系統的頻譜效率可以表示為:

(8)

其中,Rs=WHHrdGHsrF為有效接收信號的協方差矩陣,Rn為噪聲和干擾的協方差矩陣,具體表示為Rn=σ2[(WHHrdG)(WHHrdG)H+WHW]。

為了求得最大化的系統頻譜效率,需要將所有的模擬與數字預編碼器聯合進行設計。模擬預編碼器通過使用移相器對相位進行調整,將移相器的值量化為以δ=2π/2B為量化單位的具有2B個有限數量元素的量化集合Φ。該集合表示為:

Φ?{0,δ,2δ,…,(2B-1)δ}

(9)

其中,B為最大量化精度。

根據量化移相器的取值,所有模擬預編碼器的恒模約束轉變為:

(10)

其中,Γ為所有模擬預編碼器的集合。

在系統總功率的約束下,通過使用量化移相器,中繼混合預編碼優化問題可以轉化為:

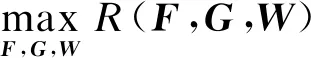
s.t.tr(FFH)≤Pr

(FRF)m,n∈Q,(WRF)m,n∈Q

(GT)m,n∈Q,(GR)m,n∈Q

(11)

為了求得式(10)中的最大化頻譜效率,需要設計每個節點的混合預編碼器。其中,源節點與目的節點的優化問題為傳統點對點優化問題,其約束條件僅與其自身節點預編碼矩陣有關,而與其他節點的預編碼矩陣無關。因此,可以通過迭代算法來對源節點與目的節點的優化問題進行求解,如采用文獻[17]中提出的基于幾何平均分解算法求得源節點與目的節點的混合預編碼矩陣F和W。本文將主要針對中繼節點的量化進行求解,不對源節點與目的節點進行贅述。

將聯合優化問題式(11)進行解耦,分離各個節點的恒模約束與功率約束,其中分離重構后的中繼節點優化問題表示如下:

(GT,GR)m,n∈Q

(12)

其中,目標函數設置為最大化該系統頻譜效率,優化約束為中繼節點的功率約束與中繼節點模擬預編碼器的恒模約束。

針對所分解出的中繼端混合預編碼優化問題,由于該優化問題需要同時對3個預編碼矩陣進行聯合優化,并且該優化問題同時具有恒模約束與功率約束的非凸約束條件。因此對混合預編碼問題分離非凸約束與功率約束,并基于稀疏近似方法進行求解。暫時不考慮模擬預編碼器的量化影響,并將優化問題轉換為范數最小化問題,具體表示為:

(13)

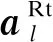
(14)

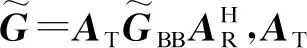
通過優化式(13)可以求得最佳數字預編碼矩陣與最佳模擬預編碼矩陣,然而所求得的模擬預編碼矩陣仍基于無限量化精度移相器,因此需要對模擬預編碼器進行量化。定義量化函數為:

(15)

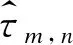
2.2 離散化正交匹配算法

與文獻[18]不同,中繼混合預編碼稀疏近似問題具有兩個天線陣列響應矩陣,并且需要對其進行聯合求解。本文提出的求解算法主要步驟如下:

輸入HsrHrd

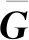
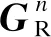
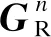
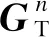
步驟5根據最小二乘法原理對數字預編碼矩陣進行求解。

步驟6通過計算無約束預編碼器與混合預編碼器之間的歸一化距離來對殘差進行更新。

步驟7對功率約束進行設計。

2.3 算法時間復雜度

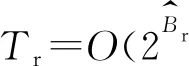
相比于文獻[7]中全精度混合預編碼算法,本文算法增加了量化處理,因此在時間復雜度方面略有增加,但是系統的能量效率卻得到了顯著提升。

3 仿真分析

為了驗證本文提出的離散化中繼混合預編碼算法的有效性,通過MATLAB對該系統的頻譜效率進行仿真分析。由于在毫米波信道中無約束的全數字預編碼器能夠達到系統的最佳性能,因此將使用全數字預編碼器[19]作為仿真對比的上限。假設系統的所有信道增益均符合高斯分布。采用1.2節中的信道環境進行傳輸,信道參數設置如表1所示。

表1 系統參數設置

圖2為輸入不同信噪比(Signal to Noise Ratio,SNR)情況下,不同數據流中不同量化精度的中繼混合預編碼頻譜效率的變化曲線,其中中繼節點發送端與接收端采用同一量化精度。由圖2可知,當數據流Ls一定時,隨著量化精度B的提高,系統的頻譜效率也越來越高,但當量化精度B增大至4 bit后,頻譜效率將不會大幅度增長。同時,增加數據流數Ls能夠明顯地提升系統的頻譜效率。因此得益于量化預編碼算法通過每次迭代對量化所造成的性能損耗進行了補償,混合預編碼器采用較低量化精度移相器就能夠達到最大化的量化頻譜效率。由于中繼節點混合預編碼器需要同時對中繼接收端和發送端進行量化處理,因此量化后的混合預編碼器與不進行量化的混合預編碼器的效果存在一定的差距。

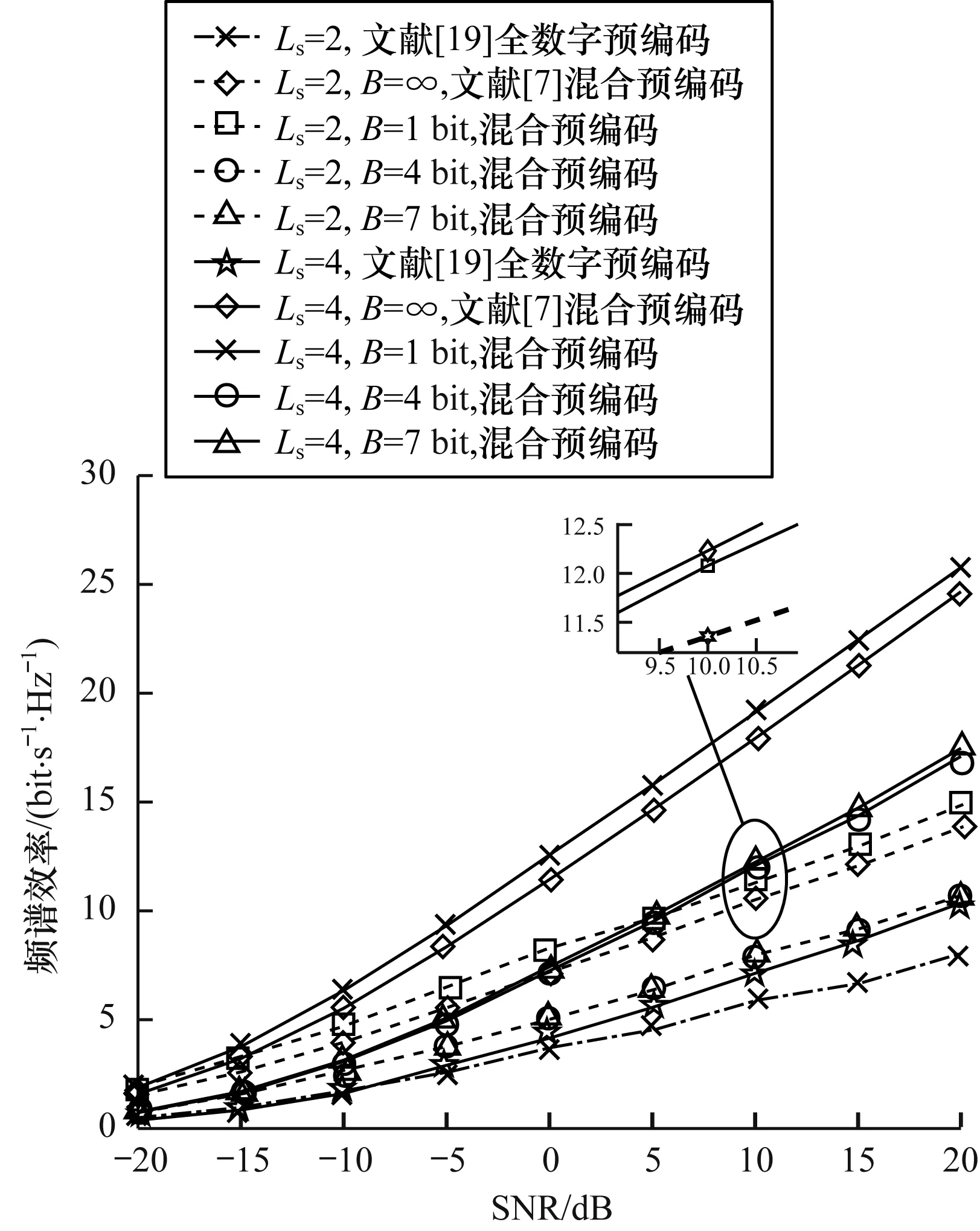
圖2 不同數據流下頻譜效率與SNR的關系

圖3為數據流Ls與RF鏈數量一定時,中繼接收端與中繼發送端單獨進行量化時頻譜效率隨著SNR的變化曲線。由圖3可以看出,當采用同樣量化精度時,量化后的接收端比量化后的發送端對頻譜效率的影響更大。同時,從單獨量化的發送端來看,當量化精度B為1 bit時,其頻譜效率與無限精度的混合預編碼器存在一定的差距,并且當量化精度為4 bit時,其頻譜效率較為接近無限精度的混合預編碼器。當對中繼節點的混合預編碼器進行求解時,需要先對接收端進行量化求解,而發送端是根據量化后的接收端所進行的優化,并且通過迭代求解將量化損耗降為更低,因此后進行量化求解的發送端具有較少的量化損耗。

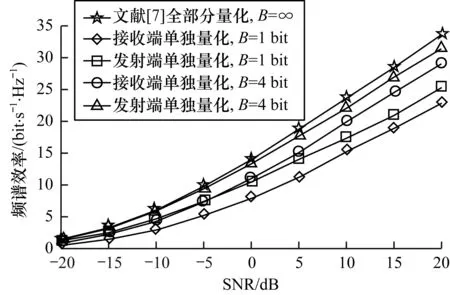
圖3 分部量化下頻譜效率與SNR的關系

圖4為在不同量化精度下,使用不同數量的RF鏈對系統頻譜效率的影響,其中系統SNR為0[20],數據流Ls=2,中繼接收端與發送端采用相同數量的RF鏈。由圖4可知,當RF鏈的數量小于5個時,不同量化精度的離散化中繼預編碼的頻譜效率均隨著RF鏈的增加而呈現增大趨勢。同時,當RF鏈的數量由2個增加至3個時,系統的頻譜效率增加顯著。此外,當RF鏈的數量增加至一定數值后,系統的性能逐漸穩定,繼續增加RF鏈的數量時,系統性能不會繼續提高,并且功耗反而增多。

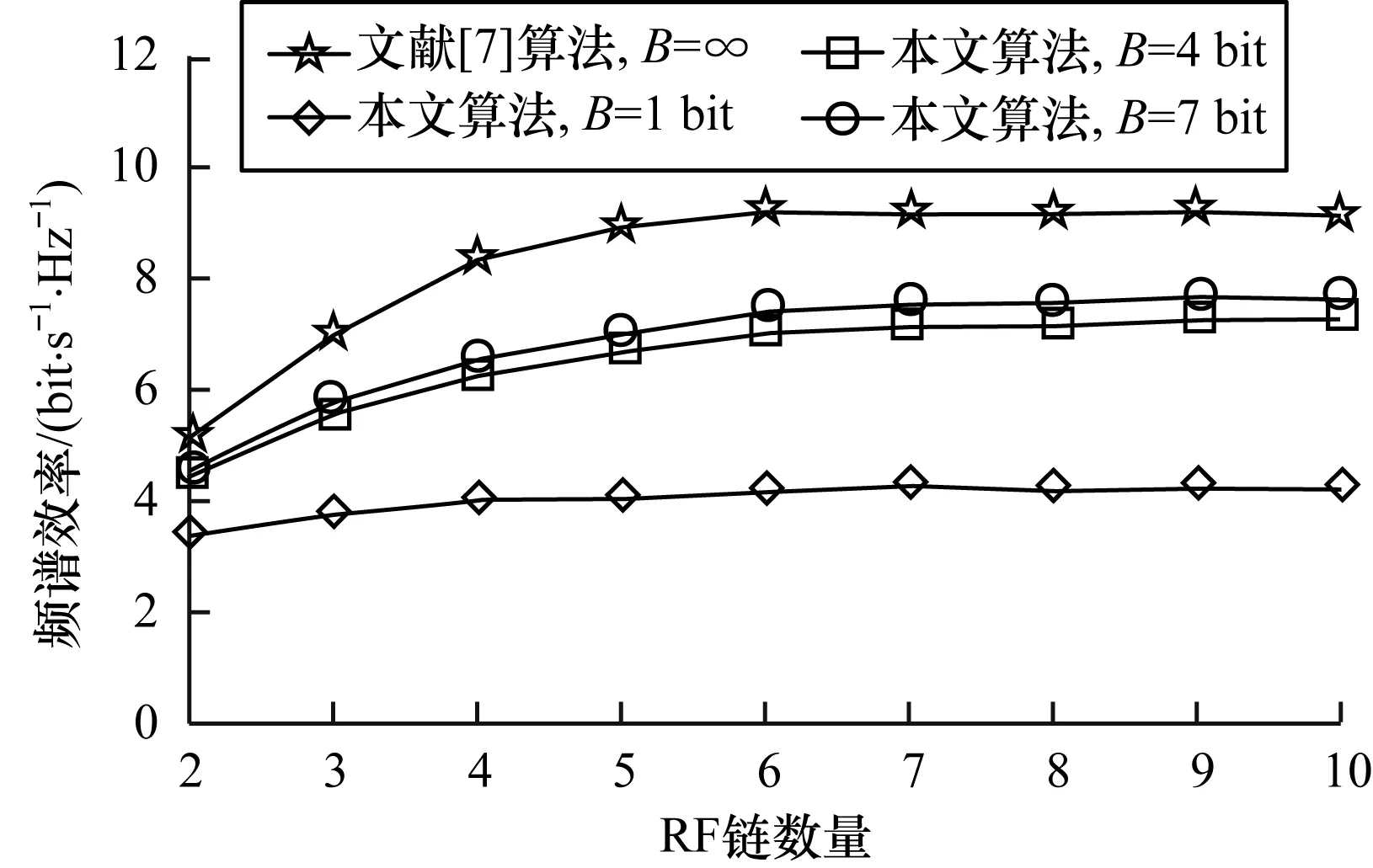
圖4 不同量化精度下頻譜效率與RF鏈數量的關系

圖5為在不同量化精度下,使用不同數量的天線情況對系統頻譜效率的影響,其中數據流Ls=8,中繼發送端與中繼接收端采用相同數量的RF鏈與天線。由圖5可以看出,當天線的數量小于50根時,不同量化精度下離散化中繼混合預編碼的頻譜效率均隨著天線數量的增加而呈現快速增長趨勢,并且當天線數量增加至一定數量后,系統的性能逐漸穩定。同時,當量化精度B達到4 bit時,中繼混合預編碼的頻譜效率接近于使用高量化精度的頻譜效率,繼續提高量化精度不能顯著增加系統頻譜效率。因此,當系統無法通過增加量化精度提高性能增益時,可以增加天線數量來提高系統性能。

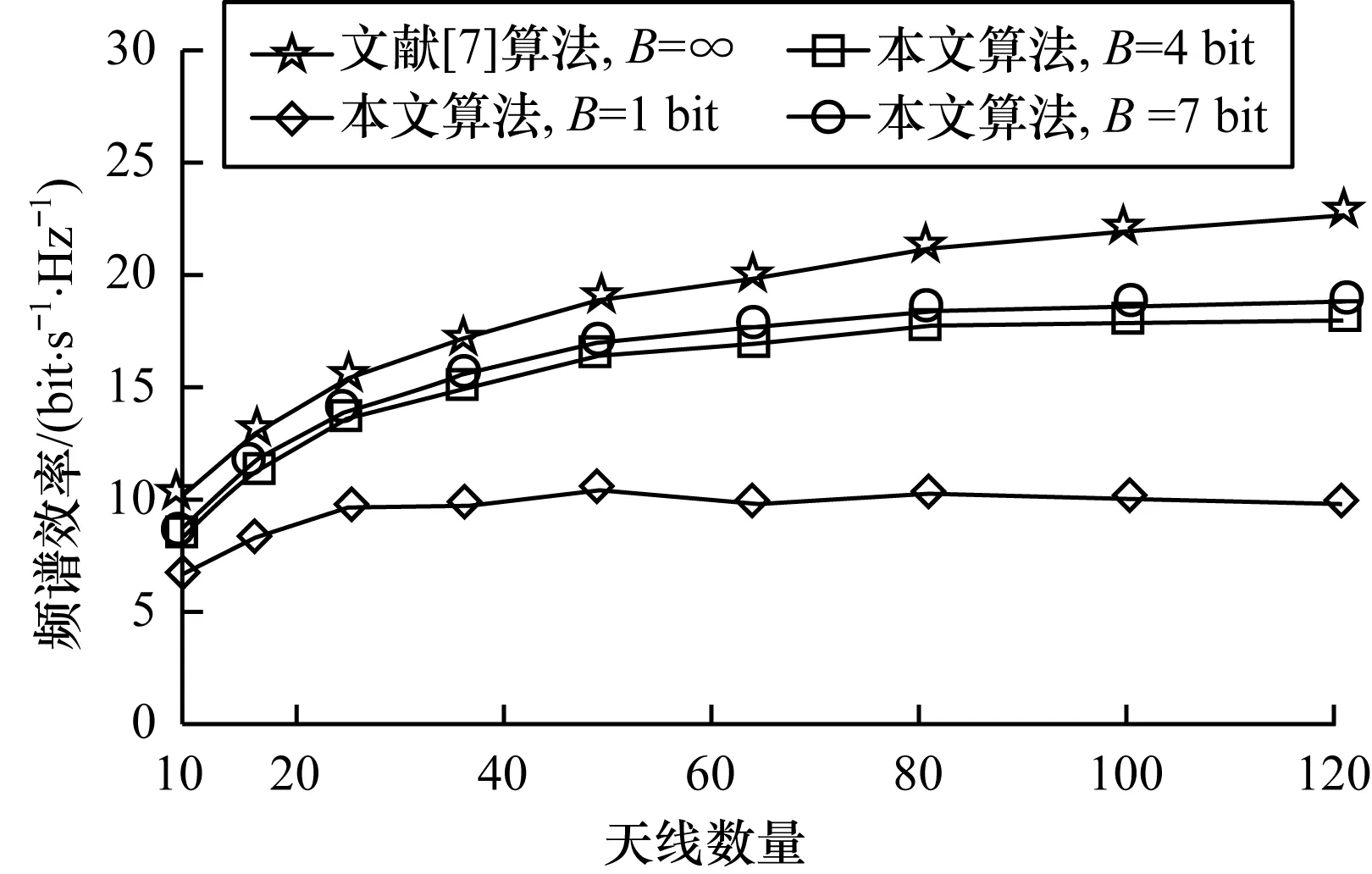
圖5 不同量化精度下頻譜效率與天線數量的關系

圖6為不同量化精度下中繼混合預編碼的能量效率隨著平均SNR的變化曲線,采用文獻[21]中的功耗參數。由圖6可知,具有低量化精度的中繼混合預編碼具有較高的能量效率,但是隨著量化精度的增加,系統能量效率逐漸減小。同時,當SNR接近10 dB時,該系統具有能量效率峰值。

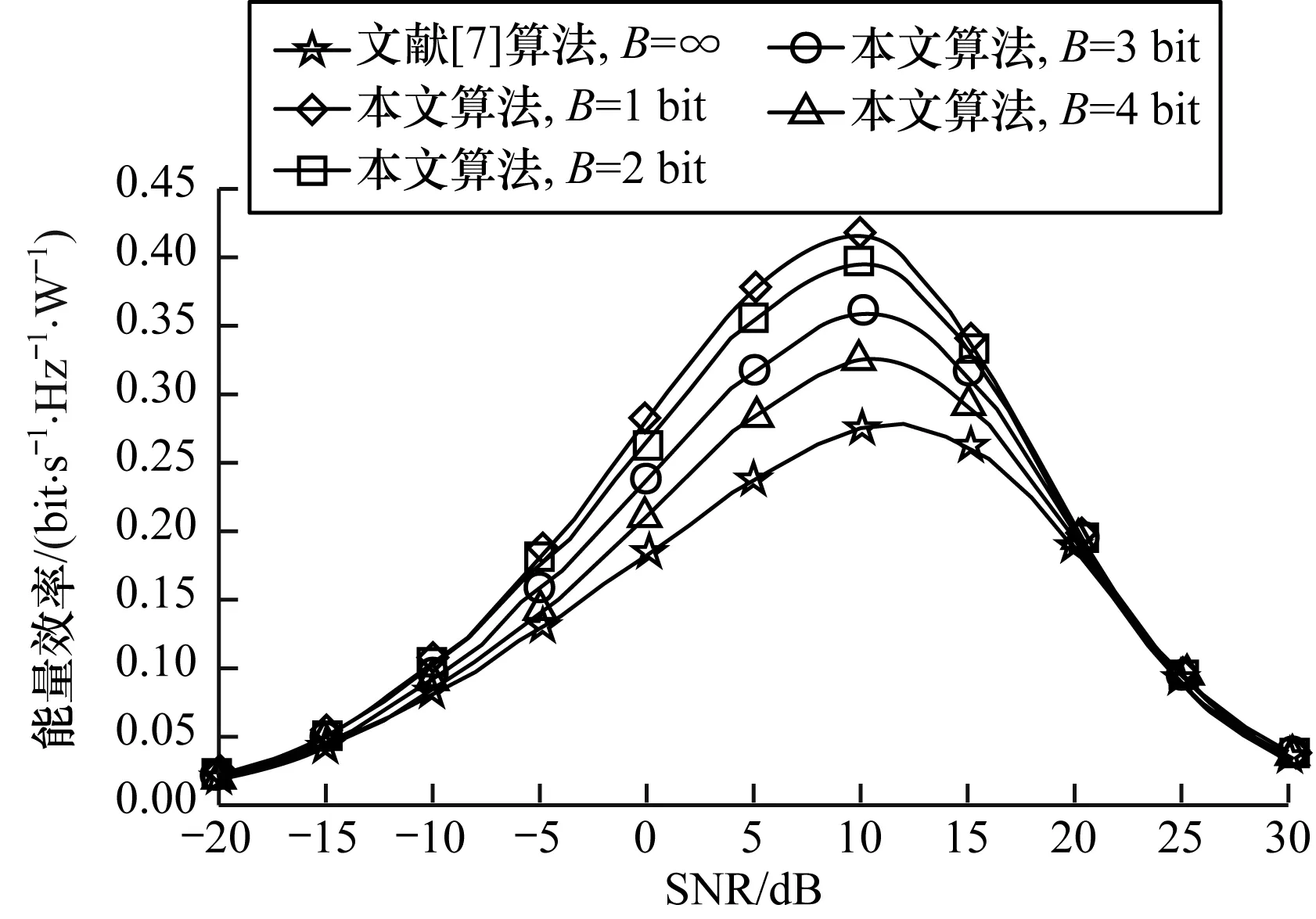
圖6 不同量化精度下能量效率與SNR的關系

圖7為輸入不同SNR條件下,不同量化精度的中繼混合預編碼的能量效率與頻譜效率的均衡變化曲線。從圖7可以看出,不同量化精度下混合預編碼的能量效率與頻譜效率變化趨勢相同,量化精度越低的混合預編碼具有越高的能量效率,但其頻譜效率相對較低。隨著頻譜效率的不斷增加,能量效率將達到峰值,但是當繼續小幅度增加頻譜效率時,能量效率卻大幅度下降。當系統頻譜效率增加至11 bit/s/Hz時,量化精度B為4 bit時的中繼混合預編碼的能量效率接近全精度量化的峰值能量效率,同時其頻譜效率也較為接近全精度量化時的頻譜效率。因此,當采用較低量化精度移相器時,在犧牲頻譜效率的前提下能夠獲得較大的能量效率。綜合考慮中繼混合預編碼的頻譜效率與能量效率,本文采用較低量化精度的移相器能夠使中繼混合預編碼在具有最大能量效率的同時獲得相對較大的頻譜效率。

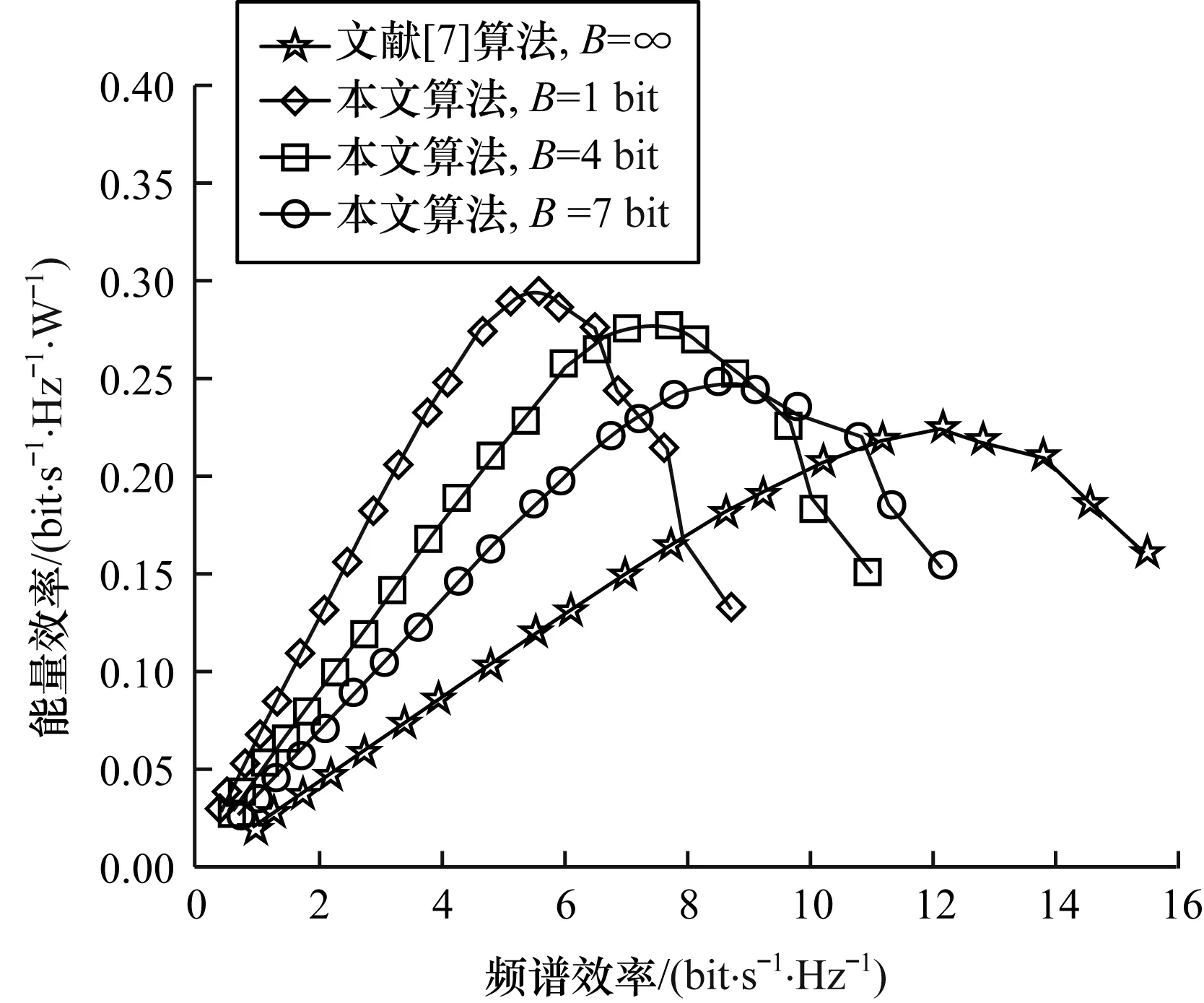
圖7 不同量化精度下能量效率與頻譜效率的均衡變化曲線

4 結束語

針對毫米波中繼大規模MIMO系統,本文提出一種基于離散化正交匹配追蹤的中繼混合預編碼算法。將中繼預編碼系統的復雜優化問題解耦為單獨節點優化問題,采用稀疏近似方法分離優化問題中的非凸約束,再利用離散化正交匹配追蹤算法對中繼節點混合預編碼矩陣進行量化求解。將本文算法與全數字預編碼和無限精度正交匹配追蹤算法進行對比,仿真結果表明,本文算法能夠在使用較低量化精度的條件下達到接近最優化的性能,并且中繼節點接收端需使用較高精度量化來抵消量化損耗,同時發送端使用較低精度量化就能達到最優性能。下一步考慮將該算法推廣至不完美信道環境下的中繼通信網絡,使其在復雜通信網絡中具有更強的適用性。