低配筋率鐵路圓端空心墩延性抗震性能分析
許 敏,邵長江
(1.中鐵二院工程集團有限責任公司,四川成都 610031;2.西南交通大學,四川成都 610031)
由于列車行車安全性對橋墩剛度要求,導致鐵路橋墩截面較大,而截面的縱向配筋率相對較低。這種低配筋率的橋墩在鐵路橋梁中廣泛應用,而因配筋率較低,橋墩變形能力較差,難以適應強震的作用。現行GB 50111-2006《鐵路工程抗震設計規范》要求鐵路橋墩應滿足:
(1)多遇地震作用下,混凝土和鋼筋混凝土橋墩均應滿足強度、偏心及穩定性驗算的要求。
(2)罕遇地震作用下,混凝土橋墩不需驗算,只需設置護面鋼筋,而鋼筋混凝土橋墩需進行延性驗算。
鐵路橋墩按照截面形式分為實心橋墩和空心橋墩。地震區的鐵路實心橋墩一般設置護面鋼筋滿足強度、偏心及穩定性驗算要求,而空心橋墩需要滿足罕遇地震作用下的延性設計要求。所以對低配筋率鐵路橋墩進行延性抗震性能分析十分必要。
目前,許多學者對低配筋率下橋墩的抗震性能做了相關研究。葉獻國等[1]基于12個鋼筋混凝土矩形橋墩的擬靜力實驗表明,在配筋率較大情況下,配箍率的提高可以有效約束核心混凝土的側向膨脹,同時可以提高橋墩的延性;但在配筋率低的情況下,箍筋的作用并不明顯。鞠彥忠[2-3]進行了10個低配筋圓端形鐓的模型試驗,得到了不同的剪跨比和配箍率對低配筋橋墩延性性能的影響規律,分析發現:縱向配筋率對混凝土橋墩的延性性能有一定的改善作用,但總體而言延性抗震性能不足;剪跨比較大的低配筋率橋墩的滯回特性有顯著差異,剪跨比對破壞形式的影響非常顯著;模型臨近破壞時,滯回耗能曲線的下降段迅速下降;配箍率對低配筋率構件的耗能影響較小;低配筋率構件的位移延性離散性較大。陳興沖等[4]系統梳理了鐵路橋墩的研究現狀,總結發現:當縱向配筋率小于0.1 %時,鐵路橋墩的位移延性系數限值建議為1.0;當配筋率在0.1 %~0.5 %范圍時,位移延性系數在1.0~4.8之間值按線性內插取值。劉浩[5]的研究表明,配筋率的提高對少筋混凝土橋墩的延性性能有一定的提高作用;配箍率的增加可以有效地約束混凝土的橫向變形,同時對橋墩的延性有一定的提高。李霖[6]的研究結果表明:縱向配筋率是影響橋墩延性性能最主要的因素。縱向配筋率的增加,可以明顯提高橋墩的極限位移及位移延性比;配箍率對于橋墩的延性性能影響不大。佐雪[7]通過振動臺試驗,研究了低配筋率鐵路圓端空心墩的抗震性能,研究表明:當配筋率接近1.0 %時,橋墩具有較好的延性性能,能夠抵御強震的作用。吳維洲等[8]通過擬靜力試驗,分析了低配筋率鐵路圓端空心墩地震損傷特性和評估方法,研究了橋墩的抗震延性,得到了與文獻[7]類似的結論,即該類橋墩抗震延性滿足設計要求。
從以上研究成果來看,限于試驗實測數據有限,有說服力的成果數量不多,各位學者對低配筋率下橋墩抗震性能上存在一定的分歧。鑒于此,本文開展了3個圓端形空心橋墩大比例縮尺模型的擬靜力試驗,采用有限元軟件OpenSees建立了鐵路圓端形空心橋墩模型,通過試驗驗證了有限元模型的合理性和正確性,在此基礎上,采用OpenSees有限元模型進行參數拓展分析,分析不同縱向配筋率、配箍率等對橋墩的水平承載力和延性性能,得出規律性的結論,為評估該類橋墩的抗震性能、進行鐵路橋墩抗震設計提供建設性的意見和建議。
1 基于試驗的有限元模型驗證
原型橋墩墩高為30 m,墩頸尺寸3.6 m×5.4 m,墩身為圓端形空心截面,墩頸壁厚0.5 m ,外坡40∶1,內坡70∶1,根據相似比理論取1∶6進行縮尺模型設計。試驗縮尺模型橋墩高為5 m,墩頸尺寸0.6 m×0.9 m,墩身截面為圓端形空心截面,內外坡與原型橋墩一致,墩底倒角處壁厚11.3 cm,墩頂倒角處壁厚7.4 cm,所有模型的混凝土標號為C35,縱筋采用直徑12 mm的HRB400帶肋鋼筋,箍筋為直徑6 mm的HPB235光圓鋼筋。建立了配箍率分別為0.325 %、0.91 %、1.51 %的三個縮尺橋墩模型進行擬靜力試驗,以觀察配箍率和軸壓比對于鐵路圓端空心墩抗震性能的影響。擬靜力試驗研究的橋墩縮尺模型參數如表1所示,結構三維模型如圖1所示。

表1 橋墩擬靜力試驗縮尺模型參數

圖1 橋墩加載及三維正面
同時,采用OpenSees軟件建立了3個縮尺模型的有限元模型對縮尺模型橋墩進行數字模擬,有限元模型計算和模型試驗所得的3個橋墩的骨架曲線如圖2~圖4所示。可見OpenSees建立的有限元模型可以較好地模擬縮尺模型的試驗結果,采用此方法建立的有限元模型可以用于橋墩設計參數的拓展研究。
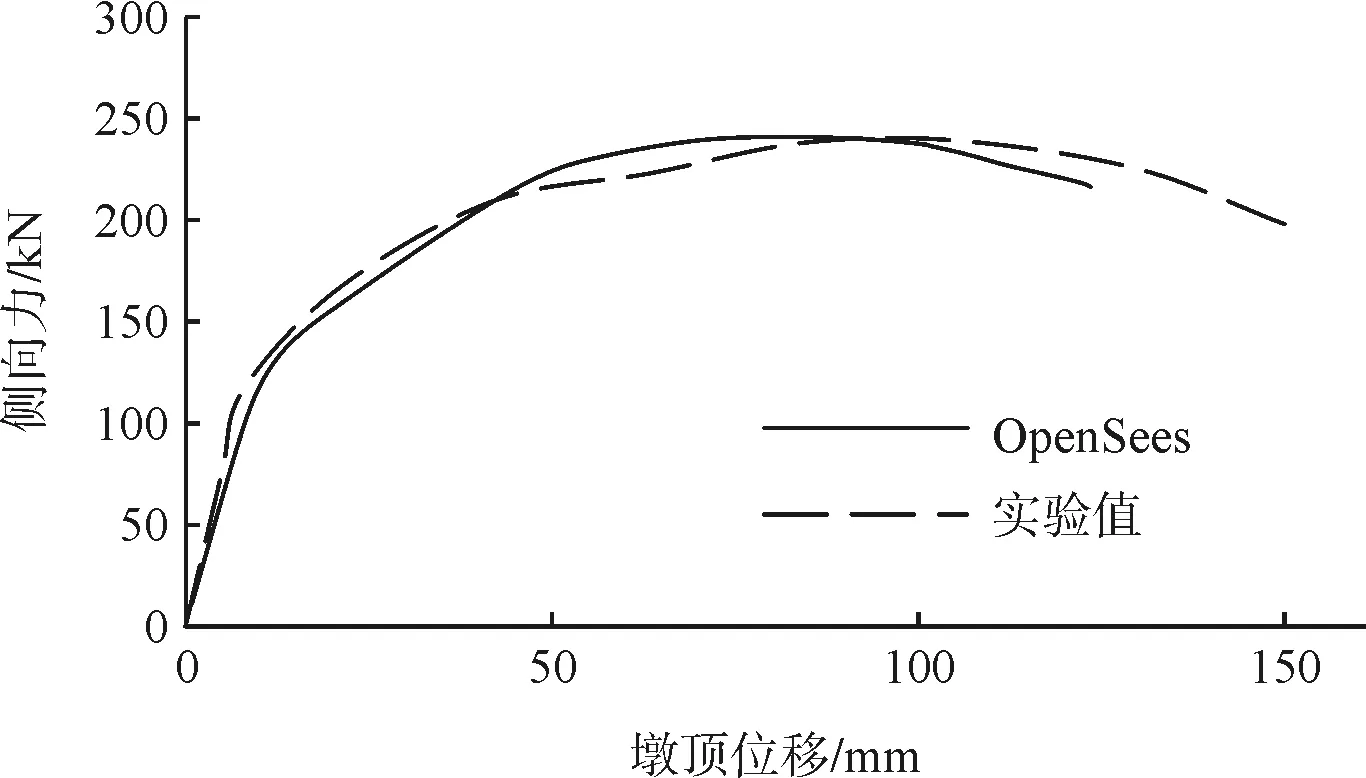
圖2 S-A1 Pushover力位移曲線
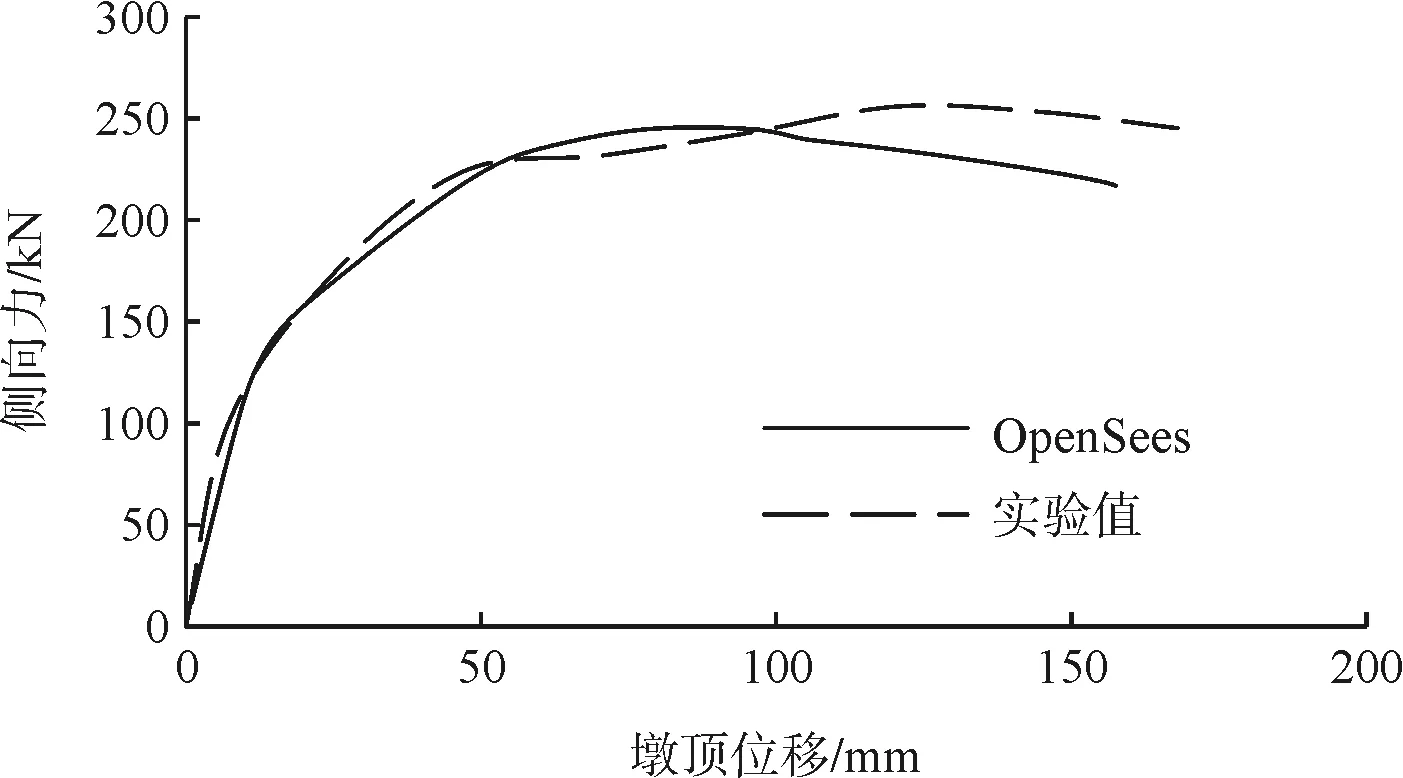
圖3 S-A2 Pushover力位移曲線
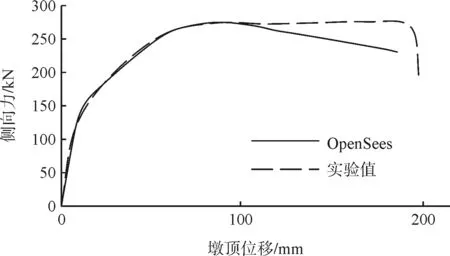
圖4 S-A3 Pushover力位移曲線
2 基于空心橋墩抗震性能研究的有限元模型建立
基于試驗驗證的有限元模型,為系統分析試驗橋墩配筋率范圍以外,配箍率和縱向配筋率對橋墩構件抗震性能的影響,并研究其變化規律,建立3組有限元模型。每組模型配箍率相同,縱向配筋率以0.1 %為間隔改變大小,從0.3 %~1.0 %依次變化,分析工況編號及分析參數如表2所示。
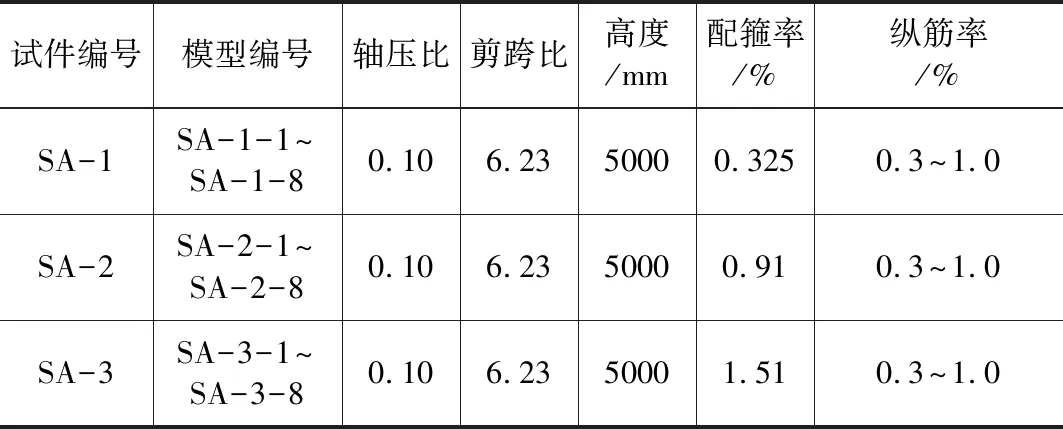
表2 有限元橋墩模型參數及編號
采用OpenSees模型,計算不同參數情況下各個有限元橋墩模型的首次屈服位移、等效屈服位移、極限位移,同時計算出橋墩模型的位移延性比、最大側向力等,計算結果詳見表3。
3 計算結果分析
由表3計算結果可知,當配箍率相同時,隨著縱向配筋率的增加橋墩所能承受的最大側向水平力、等效屈服位移、首次屈服位移、極限位移均隨之增加,比較SA-1、SA-2、SA-3三組模型計算結果發現,低配箍率橋墩的增幅沒有高配箍率橋墩的增幅大;而按照GB 50111-2006《鐵路工程抗震設計規范》計算所得的位移延性比均隨縱向配筋率的增加而減小,配箍率越高橋墩的位移延性比隨縱向配筋率增加而減小的幅度越小。從表3計算結果還可以看出,當縱向配筋率相同時,隨著配箍率的增加橋墩所能承受的最大側向水平力、等效屈服位移、首次屈服位移、極限位移均隨之增加,按照規范計算所得位移延性比也隨配箍率的增加而增加,而橋墩所承受的最大水平力變化不大,變化率不超過2.7 %。
為方便于觀察縱向配筋率及配箍率變化對橋墩抗震性能的影響規律,以縱向配筋率、配箍率為變量,繪制最大側向力、位移延性比關于縱向配筋率和配箍率的變化曲線(圖5~圖8)。

表3 有限元計算結果
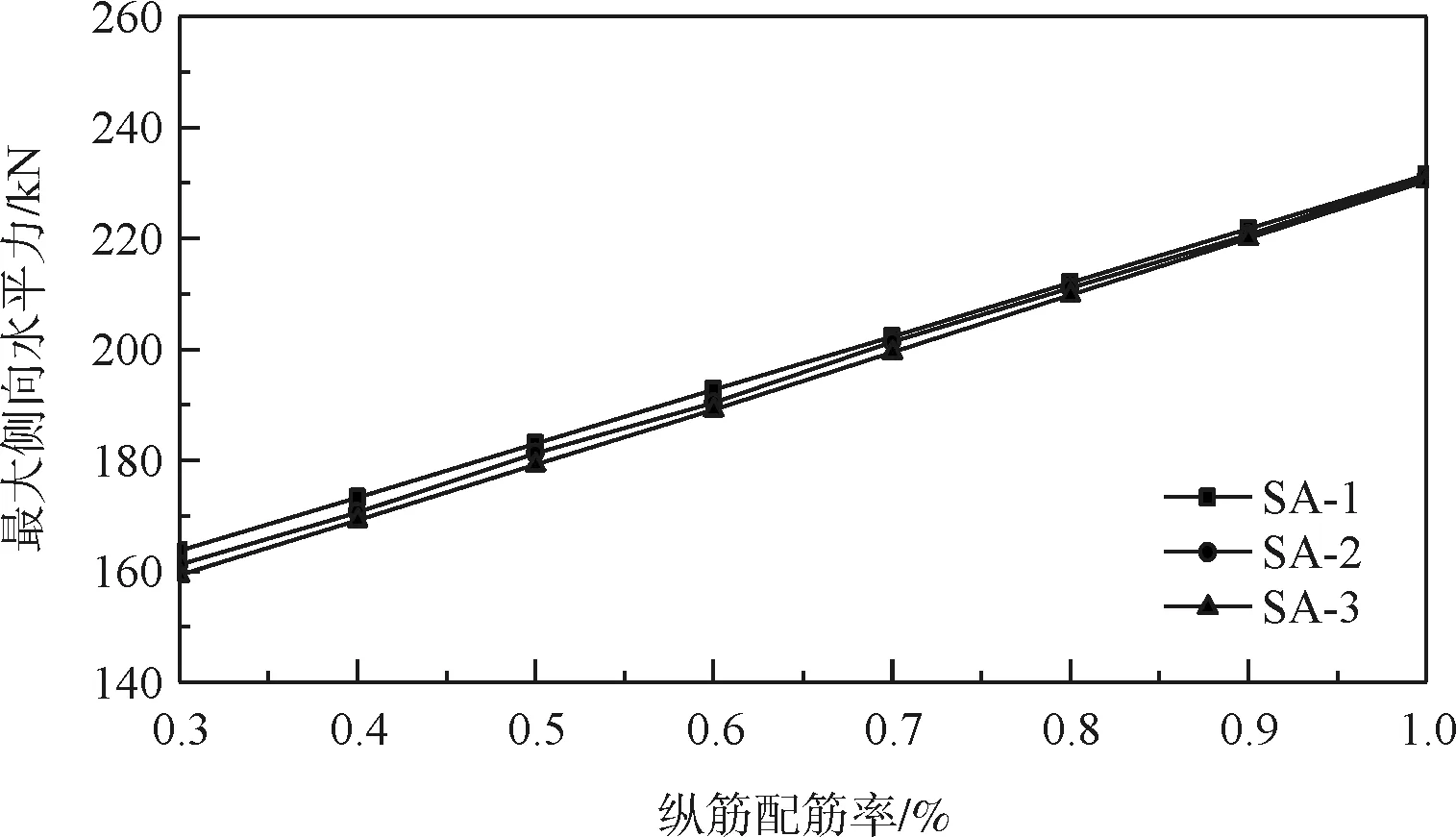
圖5 縱向配筋率與最大側向水平力的變化關系
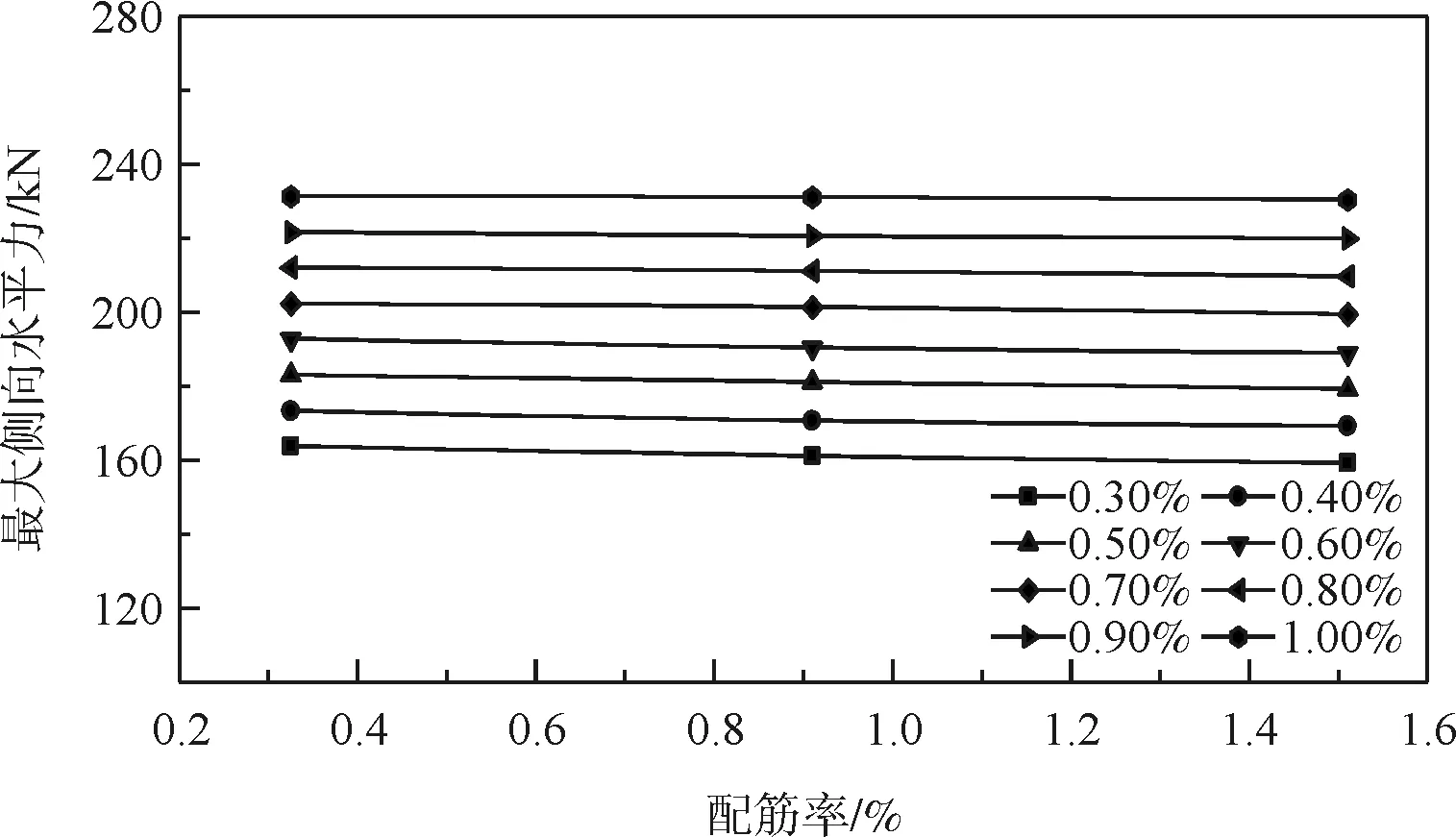
圖6 配箍率與最大側向水平力的變化關系
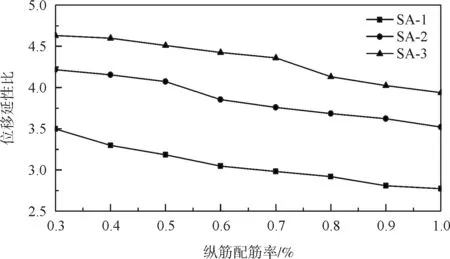
圖7 縱向配筋率與位移延性比的關系
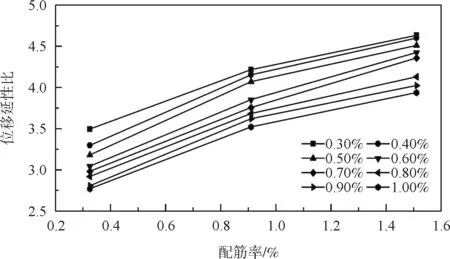
圖8 配箍率率與位移延性比的關系
從圖5可知,橋墩SA-1、SA-2、SA-3以縱向配筋率為變量,從0.3 %增加到1.0 %,橋墩的最大側向力均是呈線性增加,說明在低配箍率時,縱向配筋率對橋墩所承受的最大側向力來說比較敏感,影響較大。原因在于,增加縱向配筋率,一方面可以提高混凝土的約束效應,增加混凝土極限強度,另一方面,根據平截面假定,當截面力學平衡時,隨著縱向鋼筋面積的增加,所需外力也越大。綜上所述,縱向配筋率的提升可以有效提高橋墩的最大側向力。
從圖6可知,橋墩SA-1、SA-2、SA-3以配箍率為變量,從0.325 %到0.91 %,再到1.51 %,總體來看橋墩的最大側向水平力變化不大,最大變化量不超過2.7 %。綜上所述,在低縱向配筋率時,配箍率對橋墩所承受的最大側向力影響不大。
結合圖7與表3可知,在低配箍率情況下,隨縱向配筋率從0.3 %增大到1.0 %,橋墩的位移延性比均隨之減少。原因在于,隨著縱向配筋率的增加,結構的極限位移雖然有所增加,但相對不明顯,而屈服位移增加卻較為明顯。故在低配箍率情況下,縱向配筋率增大不能夠增強橋墩的延性能力,反而會使橋墩的延性能力降低,但極限位移卻有所增加。
從圖8可知,橋墩采用低縱向配筋率時,隨配箍率從0.325 %增大到0.91 %,再增大到1.51 %,橋墩的位移延性比隨之增大。原因在于,配箍率對約束混凝土效應的影響較大。故在低縱向配筋率情況下,增大配箍率可在一定程度上增加橋墩的延性性能。
4 結論
根據以上計算結果及分析,本文得出結論如下:
(1)橋墩采用低配箍率時,隨著結構縱向配筋率的增加,圓端形空心橋墩的墩頂最大側向承載力隨之增加,位移延性比隨之減小。故當橋墩配箍率較低時,增加縱向配筋率可以增強橋墩的側向承載能力、極限位移能力,但會減小橋墩的位移延性性能。
(2)橋墩采用低筋配筋率時,隨著配箍率的增加,圓端形空心橋墩的墩頂極限荷載變化不太明顯,但延性比隨之增加。故當橋墩縱向配筋率較低時,配箍率的增加對橋墩極限承載能力影響不大,但是可以增強橋墩的位移延性能力。
(3)當地震區鐵路橋墩設計為橋墩截面強度控制設計時,應增加縱向鋼筋,增大縱向配筋率,箍筋滿足規范要求構造需求即可;當地震區橋墩設計為延性控制設計時,應在橋墩塑性鉸區合理的設計箍筋的配箍率,以增大橋墩的極限位移與屈服位移比,即增大橋墩的延性,而不是盲目的增加縱向鋼筋,縱向鋼筋的增加反而會降低延性性能。

