LiCi算法的基于比特積分攻擊

信文倩,孫 兵,李 超

(國防科技大學(xué) 文理學(xué)院,長沙 410073)

0 概述

隨著信息時代的快速發(fā)展,物聯(lián)網(wǎng)作為信息技術(shù)的重要組成部分,其通過智能感知、識別技術(shù)與普適計算等通信感知技術(shù)廣泛應(yīng)用于網(wǎng)絡(luò)融合中。由于物聯(lián)網(wǎng)中使用的微型計算設(shè)備的計算能力有限,因此為了保證信息安全,輕量級分組密碼算法應(yīng)運而生。輕量級分組密碼算法是分組密碼算法中的一種,相比普通的分組密碼算法,該算法的分組長度相對較短,且算法結(jié)構(gòu)簡單,滿足低耗能、低成本的需求。目前,輕量級分組密碼算法主要有LED[1]、LBlock[2]、PRESENT[3]、HIGHT[4]、SPECK[5]等算法,這些算法均具有結(jié)構(gòu)簡單、加解密一致、容易實現(xiàn)等優(yōu)點。

2017年,PATIL等人[6]提出一個分組長度為64比特、密鑰長度為128比特的輕量級分組密碼算法——LiCi算法。該算法結(jié)構(gòu)類似于MISTY結(jié)構(gòu),在單輪加密結(jié)構(gòu)中,非線性組件S盒會影響到加密結(jié)構(gòu)的兩支。相較于普通Feistel結(jié)構(gòu)分組密碼算法,LiCi算法具有擴(kuò)散性快等優(yōu)勢。同時,相比于SP結(jié)構(gòu)分組密碼算法,LiCi算法對非線性組件輸出結(jié)果進(jìn)行復(fù)用,使之結(jié)構(gòu)更加簡單,具有占用面積小等特性。文獻(xiàn)[7]對LiCi算法抵抗不可能差分攻擊的能力進(jìn)行了介紹。然而,關(guān)于LiCi算法抵抗積分攻擊的能力目前尚不清楚,因此,本文利用積分攻擊方法對該算法進(jìn)行分析。

積分攻擊是KNUDSEN等人[8]在總結(jié)Square攻擊、Multiset攻擊、Saturation攻擊的基礎(chǔ)上提出的一種密碼分析方法。該攻擊方法是一種選擇明文攻擊方法,與差分攻擊[9]、線性攻擊[10]、代數(shù)攻擊[11]同為目前密碼學(xué)界公認(rèn)的最有效的幾種分析方法。結(jié)合故障分析的思想,差分故障分析[12]、代數(shù)故障分析[13]、積分故障分析[14]等分析方法也受到密碼學(xué)者們的廣泛關(guān)注。積分分析方法提出后,其在AES[15]、Camellia[16]、FOX[17]、PRINCE[18]等算法中進(jìn)行不同程度的分析應(yīng)用。文獻(xiàn)[19-20]提出比特的可分性質(zhì)后,結(jié)合MILP搜索工具,利用可分性質(zhì)對MISTY1進(jìn)行全輪攻擊。同時,文獻(xiàn)[21]也基于比特的可分性質(zhì)結(jié)合MILP搜索工具,進(jìn)一步提升LBlock[2]、PRESENT[3]、SIMECK[22]等算法的積分分析結(jié)果。

本文基于比特的可分性質(zhì),結(jié)合MILP搜索工具對LiCi算法的積分區(qū)分器進(jìn)行搜索。利用搜索得到的最長輪數(shù)的12輪積分區(qū)分器對LiCi算法進(jìn)行13輪積分攻擊,恢復(fù)17比特密鑰信息,同時,為了得到更高輪數(shù)的攻擊結(jié)果,利用10輪積分區(qū)分器向后攻擊6輪,對LiCi算法進(jìn)行16輪積分攻擊。

1 LiCi算法介紹

1.1 LiCi算法加密過程

LiCi算法分組長度為64比特,密鑰規(guī)模為128比特,其迭代輪數(shù)為31輪。LiCi算法的單輪加密結(jié)構(gòu)如圖1所示,基本操作包括字節(jié)替換、異或、密鑰加、循環(huán)移位等步驟。字節(jié)替換是該算法中唯一的非線性組件,由8個并列的4進(jìn)4出的S盒構(gòu)成。

圖1 LiCi算法單輪加密結(jié)構(gòu)

加密過程設(shè)第i輪輸入為Xi,Yi,i=0,1,2,…,29,30,分別代表第i輪輸入的左分支和右分支;輸出為Xi+1,Yi+1,分別代表輸出的左分支和右分支。狀態(tài)Xi,Yi到狀態(tài)Xi+1,Yi+1的迭代過程表示如下:

Xi+1=[S[Xi]⊕Yi⊕RK1i]<<<3

Yi+1=[S[Xi+1]⊕Xi+1⊕RK2i]>>>7

(1)

其中,RK1i,RK2i均為輪密鑰,Xi,(31,30,…,2,1,0)和Yi,(31,30,…,2,1,0)分別表示輸入狀態(tài)的64個比特的標(biāo)號,如Xi,31表示第i輪左支輸入的最高比特,Yi,0表示第i輪右支輸入的最低比特。

1.2 LiCi算法密鑰擴(kuò)展方案

密鑰擴(kuò)展方案:種子密鑰長度為128比特,記為K=K127K126…K2K1K0,RK1i,RK2i均表示第i輪輪密鑰,其中RK1i應(yīng)用于第i輪右支加密,RK2i應(yīng)用于第i輪左支加密。輪密鑰生成過程如下:

1)K=K127K126…K2K1K0

2)RK1i=K31K30K29…K2K1K0,RK2i=K63K62…K33K32,i∈{0,1,2,…}

3)Knew=K<<<13=K114K113…K1K0K127K126…K115

4)K=Knew

5)[K3K2K1K0]new=S[K3K2K1K0]

[K7K6K5K4]new=S[K7K6K5K4]

[K63K62K61K60K59]new=[K63K62K61K60K59]⊕i,i∈{0,1,2,…}

6)[K3K2K1K0]=[K3K2K1K0]new

[K7K6K5K4]=[K7K6K5K4]new

[K63K62K61K60K59]=[K63K62K61K60K59]new

7)經(jīng)過3)～6)得到新的K,返回1),經(jīng)過2)得到新的輪密鑰。

輪密鑰分析:若已知第i輪密鑰RK2i,RK1i(其中i≥5),根據(jù)密鑰擴(kuò)展方案可以得知(RK2i-4,RK1i-4),…,(RK2i,RK1i)之間的關(guān)系。

假設(shè)已知(RK2i,RK1i)=(K63…K33K32,K31…K1K0),則根據(jù)密鑰擴(kuò)展方案中輪密鑰生成方案可知(RK2i-1,RK1i-1)和(RK2i,RK1i)之間的某些比特信息等價,通過密鑰生成方案中3)～6)可知,(RK2i-1,RK1i-1)與(RK2i,RK1i)相比,新引入13比特信息。同理,可以分析(RK2i-2,RK1i-2)和 (RK2i-1,RK1i-1),…,(RK2i-3,RK1i-3)和(RK2i-4,RK1i-4)之間的關(guān)系,5輪輪密鑰總共包含116比特密鑰信息,6輪輪密鑰總共包含種子密鑰128比特密鑰信息。通過上述輪密鑰分析,利用輪密鑰之間的信息等價關(guān)系,在猜測密鑰過程中可以降低密鑰猜測量。

1.3 LiCi算法的S盒性質(zhì)

LiCi算法4比特S盒如表1所示,輸入為x,輸出為S(x)。

表1 LiCi算法S盒

采用文獻(xiàn)[23]中求S盒布爾函數(shù)表達(dá)式的方法來求解LiCi算法4比特S盒代數(shù)表達(dá)式。

性質(zhì)1(S盒代數(shù)表達(dá)式) 設(shè)S盒輸入為x=(x3,x2,x1,x0),輸出為y=(y3,y2,y1,y0),則x和y之間的關(guān)系表達(dá)式如下:

y3=x0+x1+x3+x1x2+x1x3

y2=x0+x1+x3+x0x2+x0x3+x2x3+x0x1x2

y1=1+x2+x3+x0x1+x0x2+x1x3+x2x3+x0x1x3

y0=1+x1+x2+x3+x0x1

例如,輸入x3x2x1x0=0001,經(jīng)過S盒輸出y3y2y1y0=1111。

2 基于比特的可分性質(zhì)和MILP方法

2.1 基于比特的可分性質(zhì)

定義1(比特積函數(shù)πu(x)和πU(X)[24]) 多重集的可分性質(zhì)可通過比特積函數(shù)進(jìn)行評估,比特積函數(shù)的定義如下:

其中,x[i]1=x[i],x[i]0=1。

定義3(可分路徑[21]) 考慮可分析性質(zhì)的傳播{k}?K0→K1→K2→…→Kr,對任意向量ki+1∈Ki+1使得ki能傳播到ki+1,i∈{0,1,…,r-1},則(k0→k1→…→kr)為一條r輪可分路徑。

上述內(nèi)容是關(guān)于比特積函數(shù)、可分性和可分路徑的介紹,下面對基于比特的可分性質(zhì)經(jīng)過復(fù)制操作、異或操作時的傳播規(guī)則進(jìn)行簡要介紹,更多詳情可參考文獻(xiàn)[21,24]。

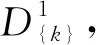
2.2 基本操作的MILP模型

基于比特的復(fù)制模型:假設(shè)輸入可分性為a,經(jīng)過基于比特的復(fù)制操作輸出可分性為(a0,a1),記作a→(a0,a1),其中a,a0,a1∈{0,1}。a,a0,a1之間的關(guān)系如下:

a-a0-a1≥0,0≤a0≤1,0≤a1≤1

例如:1→(0,1)或1→(1,0),0→(0,0)。

基于比特的異或模型:假設(shè)輸入可分性為(a0,a1),經(jīng)過基于比特的異或操作輸出可分性為a,記作(a0,a1)→a,其中a,a0,a1∈{0,1}。a,a0,a1之間的關(guān)系如下:

a-a0-a1≥0,0≤a0≤1,0≤a1≤1

例如:(0,1)→1,(1,0)→1,(0,0)→1,但是輸入可分性為(1,1),經(jīng)過異或操作可分性傳播會中斷。

S盒模型:利用文獻(xiàn)[20]中的算法2可以得到LiCi算法S盒的可分性(詳見開放科學(xué)(資源服務(wù))標(biāo)志碼中附錄部分),通過得到的S盒的可分性結(jié)合SageMath軟件可得到S盒的線性不等式組。再利用文獻(xiàn)[20]中的算法1對上述S盒線性不等式組進(jìn)行簡化,最終得到LiCi算法S盒的15個線性不等式(詳見開放科學(xué)(資源服務(wù))標(biāo)志碼中附錄部分)。

基于比特的循環(huán)移位模型:假設(shè)輸入n比特可分性為kn-1,…,k2,k1,k0,其中ki∈{0,1}。循環(huán)左移j位,輸出為k(i+n-j)mod n,i∈{n-1,…,2,1,0};循環(huán)右移j位,輸出為k(i+j)mod n,i∈{n-1,…,2,1,0}。

3 MILP方法在LiCi算法中的應(yīng)用

3.1 LiCi算法MILP模型建立

對LiCi算法的基本操作建立MILP模型,在模型建立過程中,基于比特的復(fù)制模型、異或模型和S盒模型與已有文獻(xiàn)[20]給出的模型構(gòu)造基本相同,根據(jù)LiCi算法左支循環(huán)右移7位后直接得到輸出值的結(jié)構(gòu)特性,在最后一輪利用逆向思維構(gòu)造LiCi算法MILP模型。

LiCi算法單輪可分性傳播示意圖如圖2所示。

圖2 LiCi算法單輪可分性傳播示意圖

第i(i∈{1,2,…,R-1})輪LiCi算法單輪MILP模型建立過程如下所示:

性質(zhì)1(基于比特循環(huán)移位) 在單輪函數(shù)加密結(jié)構(gòu)中,若輸入可分性經(jīng)過循環(huán)移位操作后,存在復(fù)制操作、異或操作或S盒,則直接對輸入可分性建立基于比特的循環(huán)移位模型,反之,則最后一輪輸入可分性經(jīng)過循環(huán)移位操作時利用逆向思維建立基于比特的循環(huán)移位模型。以LiCi算法為例,最后一輪(第R輪)MILP模型建立過程如下:第R輪MILP模型建立過程1)～5)和第1輪至第R-1輪模型建立過程相同,6)和7)過程如下:

3.2 LiCi算法基于比特積分區(qū)分器搜索結(jié)果

目前搜索得到的LiCi算法平衡比特數(shù)最多,輪數(shù)最長的積分區(qū)分器為輸入63比特活躍,輸出43比特平衡的12輪積分區(qū)分器。

假設(shè)a表示活躍,b表示平衡,c表示常數(shù),?表示未知,輸入兩支的單支為32比特,令標(biāo)號31表示最高位,標(biāo)號0表示最低位,輸入兩支標(biāo)號表示如下:

10輪積分區(qū)分器:基于MILP搜索得到的平衡比特數(shù)最多,輪數(shù)最長的積分區(qū)分器為輸入62比特活躍,輸出64比特平衡的10輪積分區(qū)分器,輸入記為(X0,Y0),輸出記為(X10,Y10),輸入輸出狀態(tài)表示如下:

X0:aaaa,aaaa,aaaa,aaaa,aaaa,aaaa,aaaa,aaaa

Y0:aaaa,aaaa,aaaa,aaaa,aaaa,aaca,aaaa,aaca

X10:bbbb,bbbb,bbbb,bbbb,bbbb,bbbb,bbbb,bbbb

Y10:bbbb,bbbb,bbbb,bbbb,bbbb,bbbb,bbbb,bbbb

12輪積分區(qū)分器:目前搜索得到的最長輪數(shù)積分區(qū)分器為12輪積分區(qū)分器,共有兩個積分區(qū)分器,積分區(qū)分器1是輸入63比特活躍,輸出43比特平衡;積分區(qū)分器2是輸入63比特活躍,輸出6比特平衡。輸入記為(X0,Y0),輸出記為(X12,Y12),輸入輸出狀態(tài)表示如下:

1)12輪積分區(qū)分器1

X0:aaaa,aaaa,aaaa,aaaa,aaaa,aaaa,aaaa,aaaa

Y0:aaaa,aaaa,aaaa,aaaa,aaaa,aaaa,aaaa,aaac

X12:bbbb,bbbb,bbbb,bbbb,bbbb,bb??,bb??,bbbb

Y12:???b,??bb,bbbb,bbbb,bbbb,bbbb,bbbb,b??b

2)12輪積分區(qū)分器2

X0:aaaa,aaaa,aaaa,aaaa,aaaa,aaaa,aaaa,aaac

Y0:aaaa,aaaa,aaaa,aaaa,aaaa,aaaa,aaaa,aaaa

X12:????,??b?,bb??,b???,????,????,????,????

Y12:????,????,????,???b,???b,????,????,????

4 LiCi算法的密鑰恢復(fù)攻擊

4.1 13輪密鑰恢復(fù)攻擊

由于目前基于MILP搜索得到的最優(yōu)12輪積分區(qū)分器輸入活躍比特數(shù)為63比特,輸出平衡比特數(shù)為43比特,利用12輪積分區(qū)分器時只能利用1組明文,通過猜測41比特密鑰信息,對第13輪RK212的17比特密鑰信息進(jìn)行密鑰恢復(fù)攻擊。具體攻擊過程和攻擊結(jié)果如下:

1)對構(gòu)造12輪積分區(qū)分器中263個明文進(jìn)行加密,得到263個密文C0,C1,…,C263-1。

2)猜測第13輪41比特輪密鑰RK212,(31,…,13,12,3,2,1,0),RK112,(28,25,24,23,…,13,12,3,1)解密第13輪,得到第12輪41比特輸出X12,(31,…,13,12,3,2,1,0)和Y12,(23,…,13,12,3,1)。如下表示:

X12,(31,…,13,12,3,2,1…,0)=

S-1((Y13<<<7)⊕X13⊕RK2)12,(31,…,13,3,…,0)

Y12,(28,25,24,23,…,13,12,3,1)=

((Y13<<<7)⊕X13⊕RK212)(28,25,24,23,…,13,12,3,1)⊕

(X13>>>3)(28,25,24,23,…,13,12,3,1)⊕

RK112,(28,25,24,23,…,13,12,3,1)

(2)

驗證X12,(31,…,13,12,3,2,1,0)和Y12,(28,25,24,23,…,13,12,3,1)是否為平衡比特,若為平衡比特,則猜測密鑰為正確密鑰,否則為錯誤密鑰。密鑰恢復(fù)攻擊分為兩步,第一步對輪密鑰RK212,(31,…,13,12,3,2,1,0)進(jìn)行密鑰恢復(fù)攻擊,錯誤輪密鑰使X12,(31,…,13,12,3,2,1,0)為平衡比特的概率為2-24,經(jīng)過1組明文后剩余錯誤密鑰數(shù)目為(224-1)×2-24≈1。第二步對輪密鑰RK212,(31,…,13,12,3,2,1,0)和RK112,(28,25,24,23,…,13,12,3,1)進(jìn)行密鑰恢復(fù)攻擊,錯誤密鑰使Y12,(28,25,24,23,…,13,12,3,1)為平衡比特的概率為2-17。由于第一步已經(jīng)對RK212,(28,25,24,23,…,13,12,3,1)進(jìn)行篩選,經(jīng)過1組明文后RK212,(28,25,24,23,…,13,12,3,1)剩余錯誤密鑰數(shù)目為1,經(jīng)過第二步篩選后RK212,(28,25,24,23,…,13,12,3,1)剩余錯誤密鑰數(shù)目為2-17<<1,可以恢復(fù)RK212,(28,25,24,23,…,13,12,3,1)共17比特密鑰信息。由于經(jīng)過第二步篩選,RK112,(28,25,24,23,…,13,12,3,1)錯誤密鑰量為1,因此無法對RK112,(23,…,13,12)進(jìn)行正確恢復(fù)。從而攻擊數(shù)據(jù)復(fù)雜度為263個明文,時間復(fù)雜度為263×241=2104次查32比特S盒大表,相當(dāng)于2104/16=2100次16輪加密。為猜測密鑰,攻擊需要對猜測密鑰進(jìn)行存儲,存儲復(fù)雜度為241。

針對式(2)的計算,可以通過“部分和”[25]技術(shù)對其進(jìn)行改進(jìn),具體方式如下:

步驟1猜測RK212,(31,…,13,12,3,2,1,0)的一種可能值,并計算72比特三元組(Z12,(31,…,12,3,…,0),(Y13<<<7)(31,…,13,3,…,0),X13,(31,…,13,3,…,0)),其中Z12,(31,…,13,12,3,…,0)=((Y13<<<7)⊕X13⊕RK212)(31,…,13,3,…,0),用表T記錄出現(xiàn)奇數(shù)次的三元組(Z12,(31,…,12,3,…,0),(Y13<<<7)(31,…,13,3,…,0),X13,(31,…,13,3,…,0)),求得最終結(jié)果⊕Z12,(31,…,12,3,…,0)。

步驟2猜測(RK2,RK1)12,(28,25,24,23,…,13,12,3,1)的一種可能值,對表T中標(biāo)記的每一個三元組,計算W12,(28,25,24,23,…,13,12,3,1),其中W12,(28,25,24,23,…,13,12,3,1)=Z12,(28,25,24,23,…,13,12,3,1)⊕(X13⊕RK112,(28,25,24,23,…,13,12,3,1),求得最終結(jié)果⊕W12,(28,25,24,23,…,13,12,3,1)。

若步驟1中求得的值⊕Z12,(31,…,12,3,…,0)=0,則此次猜測的RK212,(31,…,13,12,3,2,1,0)有可能是正確密鑰,否則一定是錯誤密鑰。一個錯誤密鑰滿足⊕Z12,(31,…,12,3,…,0)=0的概率為2-24。若步驟2中求得的值⊕W12,(28,25,24,23,…,13,12,3,1)=0,則此次猜測的RK212,(28,25,24,23,…,13,12,3,1),RK112,(28,25,24,23,…,13,12,3,1)有可能是正確密鑰,否則一定是錯誤密鑰。一個錯誤密鑰滿足⊕W12,(28,25,24,23,…,13,12,3,1)=0的概率為2-17,因此,1個包含263個明文的明文組可以唯一確定17比特輪密鑰RK212,(28,25,24,23,…,13,12,3,1)。

求解RK212,(28,25,24,23,…,13,12,3,1)的時間復(fù)雜度步驟如下:

步驟1對于224種RK212,(31,…,13,12,3,2,1,0)的可能值,需要處理的密文有263個,因此需要進(jìn)行287次32比特S盒查表操作。

步驟2由于一共猜測了34比特密鑰信息RK212,(28,25,24,23,…,13,12,3,1),RK112,(28,25,24,23,…,13,12,3,1),對于三元組中的每個(Z12,Y13<<<7,X13)28,25,24,23,…,13,12,3,1計算W12,(28,25,24,23,…,13,12,3,1),且(Z12,Y13<<<7,X13)(28,25,24,23,…,13,12,3,1)至多有251種可能,需要大約進(jìn)行285次32比特S盒查表操作。綜上,攻擊時間復(fù)雜度為(287+285)≈287次查32比特S盒查表,相當(dāng)于約283次16輪加密,相比于2100次16輪加密結(jié)果有了較大改進(jìn)。

4.2 16輪密鑰恢復(fù)攻擊

為了得到更長輪數(shù)的攻擊結(jié)果,結(jié)合密鑰擴(kuò)展方案的特性,本文選擇利用10輪積分區(qū)分器向后攻擊6輪,對16輪LiCi算法進(jìn)行密鑰恢復(fù)攻擊。攻擊過程至少需要猜測119比特密鑰信息。第11輪攻擊過程如圖3所示。

圖3 第11輪密鑰恢復(fù)攻擊

具體攻擊過程如下:

步驟1對構(gòu)造10輪積分區(qū)分器中262個明文進(jìn)行加密,得到262個密文C0,C1,…,C262-1。

步驟2猜測第16輪64比特輪密鑰(RK215,RK115),解密第16輪,得到第15輪64比特輸出X15,(31,30,…,2,1,0)和Y15,(31,30,…,2,1,0)。

步驟3根據(jù)步驟2的結(jié)果,猜測第15輪64比特輪密鑰(RK214,RK114),結(jié)合密鑰擴(kuò)展方案和輪密鑰的關(guān)系可以得知,這一步只需要猜測13比特信息。解密第15輪,得到第14輪64比特輸出。

步驟4根據(jù)步驟3的結(jié)果,猜測第14輪64比特輪密鑰(RK213,RK113),結(jié)合密鑰擴(kuò)展方案和輪密鑰的關(guān)系可以得知,這一步只需要猜測13比特信息。解密第14輪,得到第13輪64比特輸出。

步驟5根據(jù)步驟4的結(jié)果,猜測第13輪64比特輪密鑰(RK212,RK112),結(jié)合密鑰擴(kuò)展方案和輪密鑰的關(guān)系可以得知,這一步只需要猜測13比特信息。解密第13輪,得到第12輪64比特輸出。

步驟6根據(jù)步驟5的結(jié)果,猜測第12輪64比特輪密鑰(RK211,RK111),結(jié)合密鑰擴(kuò)展方案和輪密鑰的關(guān)系可以得知,這一步只需要猜測13比特信息。解密第12輪,得到第11輪64比特輸出。

步驟7根據(jù)步驟6的結(jié)果,猜測第11輪44比特輪密鑰(RK210,(21,20,…,2,1,0),RK110,(21,20,…,2,1,0)),結(jié)合密鑰擴(kuò)展方案和輪密鑰的關(guān)系可以得知,這一步只需要猜測3比特信息。解密第11輪,得到第10輪42比特輸出(X10,(19,…,2,1,0),Y10,(21,20,…,2,1,0)),具體表示如下:

X10,(19,…,2,1,0)=S-1((Y11<<<7)⊕X11⊕RK210)(19,…,2,1,0)

Y10,(21,20,…,2,1,0)=((Y11<<<7)⊕X11⊕RK210)(21,20,…,2,1,0)⊕

(X11>>>3)(21,20,…,2,1,0)⊕

RK110,(21,20,…,2,1,0)

(3)

驗證X10,(19,18,…,2,1,0)和Y10,(21,20,…,2,1,0)是否為平衡比特,若為平衡比特,則猜測密鑰為正確密鑰,否則為錯誤密鑰。

步驟8重新選擇一組構(gòu)造10輪積分區(qū)分器的明文,重復(fù)步驟1～步驟7直至密鑰唯一確定。

結(jié)合密鑰擴(kuò)展方案和輪密鑰的分析,上述攻擊共需要猜測119比特密鑰信息。對于正確密鑰可以保證X10,(27,26,…,1,0)和Y10,(27,26,…,1,0)為平衡比特,錯誤密鑰使X10,(27,26,…,1,0)和Y10,(27,26,…,1,0)為平衡比特的概率為2-42,經(jīng)過1組明文后剩余錯誤密鑰數(shù)目為(2119-1)×2-42≈277,為確定唯一密鑰需要3組明文,剩余錯誤密鑰數(shù)量為(2119-1)×2-42×3≈2-7。從而攻擊數(shù)據(jù)復(fù)雜度為262×3=263.6個明文,時間復(fù)雜度為262×(2119+277+235)≈2177次查32比特S盒大表,相當(dāng)于2177/16=2173次16輪加密。為猜測密鑰,攻擊需要對猜測密鑰進(jìn)行存儲,存儲復(fù)雜度為2119。由于利用10輪積分區(qū)分器向后擴(kuò)展6輪對LiCi算法進(jìn)行16輪積分攻擊,第10輪輸出和第16輪密文信息以及第12～第16輪的輪密鑰的每一比特信息均幾乎相關(guān),因此未能利用“部分和”技術(shù)降低時間復(fù)雜度。

根據(jù)攻擊步驟1～步驟8結(jié)合LiCi算法密鑰擴(kuò)展算法可知,利用10輪積分區(qū)分器向后擴(kuò)展2輪～6輪時,攻擊時間復(fù)雜度均大于2128。

5 結(jié)束語

本文將基于比特的積分性質(zhì)和MILP搜索工具相結(jié)合,得到平衡比特數(shù)目最多、輪數(shù)最長的積分區(qū)分器為12輪積分區(qū)分器,利用12輪積分區(qū)分器對LiCi算法進(jìn)行13輪積分攻擊,攻擊數(shù)據(jù)復(fù)雜度約為263,時間復(fù)雜度約為2100次16輪加密,存儲復(fù)雜度約為241。利用“部分和”技術(shù)可以將時間復(fù)雜度降為283次16輪加密。為得到更長輪數(shù)的攻擊結(jié)果,利用構(gòu)造的10輪積分區(qū)分器向后攻擊6輪,對16輪算法實施密鑰恢復(fù)攻擊,攻擊數(shù)據(jù)復(fù)雜度約為263.6,時間復(fù)雜度約為2173次16輪加密,存儲復(fù)雜度約為2119。本文在積分攻擊層面對LiCi算法進(jìn)行分析,結(jié)果表明,13輪LiCi算法不能抵抗積分攻擊。下一步將基于比特的可分性,在搜索積分區(qū)分器時對輸入可分性的初始值和積分區(qū)分器的輪數(shù)與平衡比特數(shù)目之間的關(guān)系進(jìn)行研究。