附加彈簧保護裝置的懸索主共振響應分析

張鵬 盧文勝 呂西林

摘要：在索端附加彈簧保護裝置可以減少外部環境振動對索網幕墻正常使用的影響，然而，索端附加彈簧保護裝置會顯著改變其靜力和動力特性。為分析該保護裝置對索結構靜力和動力特性的影響，通過建立附加彈簧保護裝置懸索的靜力和動力非線性方程，求得頻率的特征方程和振型的閉合解，并利用多尺度法求解主共振響應的近似解和幅頻響應方程。分析了附加彈簧與懸索剛度比對不同垂度懸索的靜力性能、前三階頻率和幅頻響應的影響規律。結果表明：為將索變形控制在工程允許的范圍內并同時降低最大索力響應，建議在工程上將附加彈簧剛度與懸索線剛度比取值在0.2到2之間。研究成果可以為索網幕墻附加彈簧保護裝置的抗風和抗震的初步設計提供參考。關鍵詞：非線性振動;主共振;懸索;彈簧保護裝置;幅頻響應

中圖分類號：O322;TU382文獻標志碼：A 文章編號：1004-4523（2020）03-0550-09

DOI：10.16385/j.cnki.issn.1004-4523.2020.03.014

引言

索網幕墻具有結構自重輕、承載能力大、高通透性等特點，廣泛地運用于工程結構中。在懸索端附加彈簧保護裝置，如北京新保利大廈、北京土城電話局、韓國世界貿易中心等，具有諸多優點，主要有：緩沖沖擊荷載;減少溫度作用引起的索力變化和預應力松弛現象;減少主體結構變形對索結構的影響，使索變形集中在彈簧裝置上，避免索結構破壞;用于相鄰建筑結構間的索網幕墻中，地震作用下吸收相鄰結構之間的相對變形，保護索網幕墻，因此，在工程實踐中有廣泛的應用前景。

索網幕墻質量輕、剛度小，易受外部環境振動的影響，國內外學者對索網幕墻在風荷載和地震作用下的動力響應做了大量的研究工作，并取得了豐碩的研究成果。在抗風方面，Wu等采用頻域法研究了單層索網的風致響應，研究表明索網的第一階模態占有主導作用，對風致響應貢獻較大的模態分布在低階模態的窄帶內。Yu等采用時域分析法研究了L形索網幕墻的風致響應，分析了索網幕墻在不同角度風荷載作用下的變形、加速度和索力響應，提出了風振系數的建議取值。馮若強等推導了基于非線性隨機振動理論的單層平面索網幕墻結構風振響應計算公式，提出了單層索網幕墻結構非線性抗風設計方法。在抗震方面，Feng等對索網幕墻進行了振動臺試驗研究和數值分析，研究表明：幕墻玻璃的彎曲剛度對索網幕墻的1階模態貢獻較小，而主要影響其高階模態;索網幕墻的抗震性能主要受對稱模態的影響，第一振動模態起控制作用。馮若強等分析了單層平面索網幕墻結構地震反應，提出了地震下索網幕墻結構需要考慮的振型階數，并建議了索網幕墻的抗震設防水準。石永久等采用幾何非線性時程分析法，討論了影響不同幾何非線性的單層索網的諧波地震響應，研究表明，索網長寬比及索預應力對幾何非線性影響較大，單層索網動力響應存在峰值共振偏移現象。

懸索單元是索網幕墻的基本受力構件，其動力特性直接影響索網幕墻的動力響應。由于索的幾何非線性，動力作用下索的振動問題是復雜且有趣的，并引起了大量國內外學者的關注，其中懸索的非線性共振現象是一個熱點。當激勵頻率接近索的線性自振頻率時，會引起索的非線性主共振現象，Bene-dettini等和Arafat等推導了簡諧荷載作用下索的非線性動力方程，給出了主共振下的幅頻響應解析公式，分析了分岔等非線性現象;當索的平面內對稱模態頻率接近于平面內反對稱模態頻率和平面外模態頻率時，會引起索的1：1和2：1內共振現象;當激勵頻率整數n或1/n倍于索的線性自振頻率會引起索的分諧振動現象。

索端附加彈簧保護裝置會顯著改變其靜力和動力特性。相關研究表明索網幕墻的抗震和抗風性能主要由平面內1階模態起控制作用。因此，選擇懸索平面內模態和工程師較為關注的平面內主共振為研究對象，建立了懸索附加彈簧保護裝置的靜力和動力非線性方程，求得了頻率的特征方程和振型的閉合解，并利用多尺度法求解主共振響應的近似解和幅頻響應方程。將附加彈簧與懸索剛度比作為關鍵參數，重點分析了該參數對不同垂度懸索的靜力性能、前三階頻率和幅頻響應的影響規律并給出了建議取值范圍。本文的研究成果可以為索網幕墻附加彈簧保護裝置的抗風和抗震初步設計提供參考。

1 數值模型建立及無量綱化

簡諧荷載作用下懸索附加彈簧保護裝置振動的簡化模型如圖1所示。懸索左端鉸接于支座O，右端鉸接于附加彈簧裝置的支座A，x向為懸索縱向，y向為懸索橫向，彈簧剛度為k，單索跨度為l，在靜力荷載作用下索的跨中變形為b，簡諧荷載為Fcos（Ωt）。本文僅研究由簡諧荷載激勵下的平面內單模態主共振響應。懸索振動符合如下假定：

（1）索在靜力荷載作用下垂度（b/l）小于1/8，索的縱向振動符合準靜態假定，忽略索縱向振動的慣性力;

（2）忽略索的抗彎、抗扭和抗剪剛度;

（3）未考慮模態耦合引起的內共振。

簡諧荷載作用下懸索平面內振動方程為：

2 力學平衡方程

2.1 靜力平衡方程

彈簧保護裝置會顯著影響懸索的靜力學性能，因此，在動力分析前，有必要對附加彈簧裝置索的靜力學性能進行分析。假設懸索在靜力均布荷載F₀作用下由初始索線型y=0慢速變化到線型w，因此，將方程（8）的慣性力項和速度項忽略，得到靜力平衡方程

2.2 模態和頻率方程

為了研究附加彈簧裝置懸索的線性頻率，令振動方程（8）和邊界條件方程（6）的阻尼項、荷載項及非線性項等于零，得到懸索的無阻尼線性自由振動方程和邊界方程

2.3 多尺度法求解非線性動力方程式中a₀為位移幅頻響應，r₀為相位角，u為懸索的阻尼比。由以上推導過程可知，懸索端部彈簧裝置的剛度貢獻主要通過非線性系數。二來體現。

3 結果與討論

3.1靜力分析

為研究彈簧剛度對不同垂度索靜力性能的影響規律，根據《索結構技術規程》對單層平面索網幕墻最大垂跨比為1/45的要求，選取3種索-I型索、Ⅱ型索和Ⅲ型索。當彈簧剛度為無窮大時，懸索的物理剛度a均為500，對應索的垂跨比b分別約為1/150，1/75和1/60，如表1所示。

根據靜力計算公式（10），γ_k對垂跨比b和索力h₀的影響規律如圖2和3所示。總體上隨著γ_k減小，b增大，而相應的h₀減小，說明靜力荷載作用下，邊界約束削弱會引起索變形增大而相應的索力減小。隨著垂跨比b增大，γk對b和h。的影響程度增大，對于I-Ⅲ型索，當γ_k從10²變化到0.1，b分別增加了5%，17%和22%，而h。分別降低了5%，20%和28%，γ_k=0.1時，I-Ⅲ型索的垂度均小于1/45.從γ_k對b和h。變化速率的影響分析，當γ_k從0.1到2時，b和h。變化較快，當γ_k變化大于2時，b和h₀變化不明顯，當γ_k趨于無窮大時，邊界約束為固定端，實際上在靜力計算時，當γ_k大于20時，可以認為是固接。當γ_k>2時，與固接相比三類索的b和h₀變化均小于10%，而當γ_k<0.2時會引起彈簧的變形過大，不利于工程應用。因此，為將索變形控制在工程允許的范圍內并同時降低索力，建議在工程上將γ_k取值在0.2到2之間。其中，垂跨比較大的索取區間內的較大值，垂跨比較小的索取區間內的較小值。

3.2 模態頻率分析

反對稱模態頻率和模態公式（13）不含γ_k系數，說明附加彈簧裝置不影響索反對稱模態的頻率和模態，其動力特性和固定端一致，因此，本文重點分析索的正對稱模態動力特性。考慮附加彈簧后的系數a₁b²是綜合反映索的物理剛度和幾何剛度的重要參數，當a₁b²增大時，索的剛度增加。為研究附加彈簧剛度對a₁b²系數及頻率的影響規律，通過調節索初始張拉力H₀，在相同靜力荷載作用下讓同類型索在附加不同剛度的彈簧裝置后具有相同的垂跨比b和索力h₀。當附加彈簧剛度為無窮大，3種索的a₁b²系數分別為0.024，0.14和0.24.

彈簧剛度γ_k對系數a₁b²和正對稱模態前三階頻率的影響規律如圖4所示。分析圖4可知：總體上，對于相同類型索，隨著γ_k增大，a₁b²系數和正對稱模態前三階頻率均增大;γ_k對前三階頻率的影響程度不同，γ_k對第1階頻率影響較大，而對第2和第3階頻率影響非常小，例如，對于Ⅱ型索，當γ_k從0.1增加到10³時，1階頻率增大28%，而2階和3階頻率僅增大0.4%和0.05%;從γ_k對a₁b²系數和頻率影響的變化速率分析，與靜力計算結果類似，γ_k從0.1到2時，a₁b²系數和頻率變化速率較快。γ_k>2時，a₁b²系數和頻率變化速率慢;從不同類型索分析，垂跨比越大，γ_k對索的1階頻率的影響越大，當γ_k從0.1增加到10³時，Ⅲ型索（垂跨比1/60）的1階頻率增大41%，Ⅱ型索（垂跨比1/75）1階頻率增大28%，1型索（垂跨比1/150）1階頻率增大5.5%。

3.3 主共振下索的非線性響應分析

3.3.1γ_k對幅頻響應a₀的影響規律

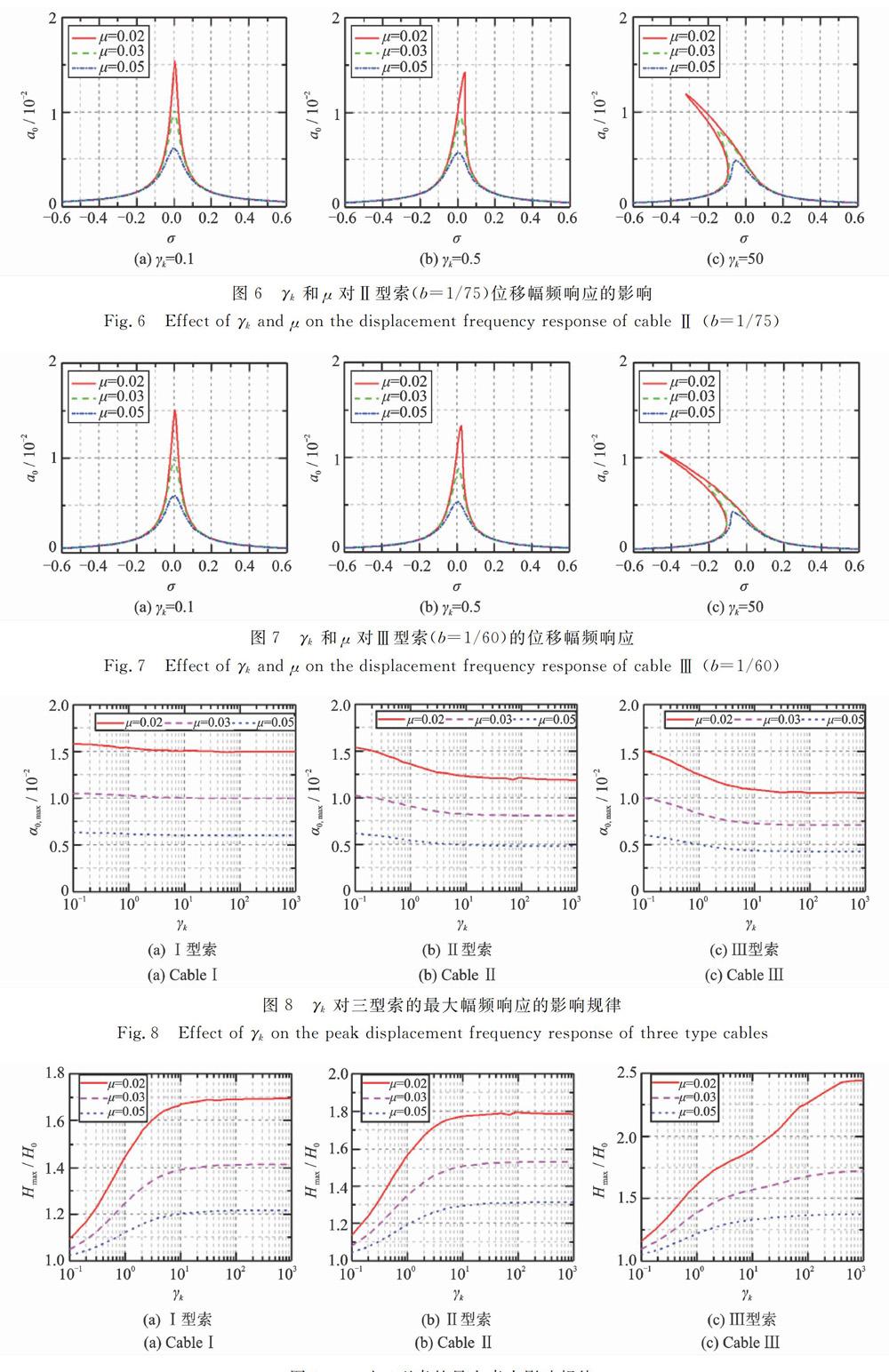
根據懸索附加彈簧裝置位移幅頻響應公式（26），荷載幅值F_k=0.002，考慮不同阻尼比u和剛度比γ_k，三型索的主共振下位移幅值響應曲線分別如圖5-7所示，橫坐標為解諧參數δ，縱坐標為索穩態響應的幅頻響應a₀。由圖5可知：I型索的幅頻響應曲線均向右彎曲，表現為“硬彈簧”的非線性特性，與文獻中無垂度索振動特性一致。當γ_k=50時，幅頻響應的彎曲曲率大，索具有較強的非線性，隨著附加彈簧剛度減小，彎曲曲率降低，當γ_k=0.1時，懸索體現出弱非線性。其主要原因為索的非線性項主要包含平方項系數和立方項系數，隨著附加彈簧剛度減小，考慮端部彈簧的物理剛度a1降低，索的平方和立方項系數均減小，所以呈現出弱非線性特征。由圖6和7可知：γ_k=50時，Ⅱ型和Ⅲ型懸索的幅頻響應曲線均向左彎曲，表現為“軟彈簧”的非線性特性，與文獻中有垂度索振動特性一致，且與1型索一致，隨著附加彈簧剛度減小，索表現出弱非線性特征。

3.3.2 阻尼比對幅頻響應的影響規律

對于索網幕墻，幕墻為索網結構附加一定的阻尼，因此，有必要分析阻尼對索振動特性的影響。考慮了3種阻尼比（μ=0.02，0.03和0.05）對幅頻響應的影響規律，由圖5-7可知，隨著阻尼比增大，三型索的最大幅頻響應a_0，max（即幅頻響應曲線的峰值點）均逐步降低且曲線更加平緩。同時，當索的非線性較強時，例如當γ_k=50時，隨著阻尼比增加，索的幅頻響應曲線彎曲程度也逐步降低，說明隨著阻尼比增大，索表現出弱非線性。

3.3.3 γ_k對最大幅頻響應a_0，max的影響規律

γ_k對最大幅頻響應的影響規律如圖8所示。總體上，隨著γ_k減小，索的最大幅頻響應均增大，隨著阻尼增大，最大幅頻響應減小。γ_k對垂跨比不同三型索的最大幅頻響應的影響程度不一樣，γ_k對垂度大懸索的最大幅頻響應影響程度大，例如：當阻尼比為0.02時，γ_k從10³減小到0.1，I型、Ⅱ型和Ⅲ型索的最大幅頻響應分別增加了6%，30%和40%，垂度最大的Ⅲ型索的最大幅頻響應變化最大。從最大幅頻響應的速率上分析，當γ_k小于2時，最大幅頻響應變化速率相對較快，當γ_k大于2時，變化速率慢。

3.3.4γ_k對最大索力響應H_max的影響規律

索力是工程實踐中重點關注的另外一個指標，γ_k對最大索力H_max（即索力的最大值）的影響規律如圖9所示。總體上，與變形相反，隨著γ_k減小，最大索力響應H_max均增大。而隨著阻尼增大，最大幅頻響應a_0，max減小，值得關注的是隨著阻尼的增大，索的變形和索力均同時降低。與最大幅頻響應相同，γ_k對垂跨比不同三型索的H_max影響程度不一樣，γ_k對垂度大懸索的最大索力響應影響程度大，例如：當阻尼比為0.02時，γ_k從10³減小到0.1，I-Ⅲ型索的H_max分別減小了35%，38%和48%。

通過靜力計算分析和幅頻響應分析，為將索變形控制在工程允許的范圍內并同時降低最大索力響應，建議在工程上將γ_k取值在0.2到2之間。其中，垂跨比較大的索取區間內的較大值，垂跨比較小的索取區間內的較小值。

4 結論

建立了懸索附加彈簧保護裝置的靜力和動力非線性方程，求得了頻率的特征方程和振型的閉合解，并利用多尺度法求解主共振響應的近似解和幅頻響應方程。分析了彈簧剛度對懸索的靜力性能、前三階頻率和幅頻響應的影響。得到的主要結論如下：

（1）靜力分析結果：隨著附加彈簧剛度與索軸向線剛度的比值γ_k減小，索垂跨比增大，而相應的索力減小。索垂跨比增大時，γ_k對索變形和索力的影響程度影響越明顯。

（2）頻率分析結果：γ_k未影響索反對稱模態的頻率。對于索的正對稱模態，隨著γ_k增大，第1階頻率明顯增大且當γ_k從0.1變化到2時頻率變化速率較快，而對第2和第3階頻率影響非常小。

（3）主共振非線性響應分析結果：隨著γ_k減小，索的幅頻響應曲線彎曲程度降低，索體出現較弱的非線性，最大索力響應降低而最大幅頻響應增大;隨著阻尼比增大，索呈現出較弱的非線性，最大索力響應和最大幅頻響應均減小;垂跨比越大的索，γ_k對索力和位移響應影響越明顯。

（4）為將索變形控制在工程允許的范圍內并同時降低最大索力響應，建議在工程上將γ_k取值在0.2到2之間。其中，垂跨比較大的索取區間內的較大值，垂跨比較小的索取區間內的較小值。