非穩態橫風對貨運動車組車體-集裝器系統橫向振動特性的影響

薛蕊 任尊松 查浩 張明

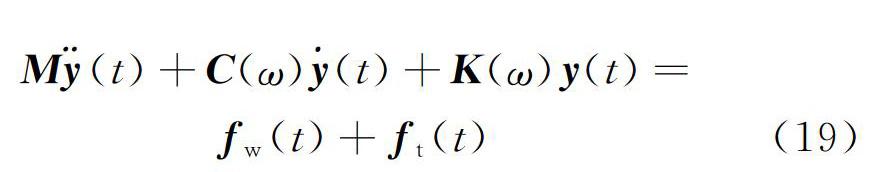
摘要：基于Cooper理論構建了平均速度20m/s的非穩態風譜及相應的側風載荷和側滾力矩載荷，并加載到貨運動車組車體-集裝器耦合模型中，分析了勻質集裝器重心為其幾何中心處，車體-集裝器系統在風載激勵和風載與軌道不平順耦合激勵作用下不同風速的橫向加速度RMS值的變化規律，以及該系統在上述兩種工況及武廣軌道不平順激勵工況下的橫向振動的頻域特性。結果表明：貨運動車組車體-集裝器系統的橫向振動加速度隨風速的增加而增加;軌道不平順激勵與風載激勵相互疊加后，可改變車體-集裝器系統的橫向振動時頻域特征以及車體至集裝器的橫向振動傳遞特性;橫風載荷對貨運動車組車體-集裝器系統的低頻振動影響不容忽視。

關鍵詞：橫風載荷;橫向振動;貨運動車組;Cooper理論

中圖分類號：U260.11;U271.91文獻標志碼：A 文章編號：1004-4523（2020）03-0540-10

DOI：10.16385/j.cnki.issn.1004-4523.2020.03.013

引言

隨著中國高鐵線路圖的不斷擴展，為提高鐵路運力，充分利用高鐵網絡，同時也為滿足國家戰略需求，中國正在高速客運列車組的基礎上研發高速貨運動車組，該動車組擬運行速度在250km/h及以上。當貨運列車在高速運行的情況下，由于其內部裝載集裝器及貨物，其車體振動與客車車體振動有所不同。

橫風作為列車運行過程中常見的一種工況，對列車系統的振動具有重要的影響。國內外學者對大風或橫風工況的車輛系統振動特性做了一系列深入研究。Olmos等在研究風-車-橋系統的耦合振動特性時發現，風速越大，車體的橫向振動越明顯。JI等的研究結果表明，風載對車體的振動特性有較大的影響，而軌道激擾對輪對的振動特性的影響較大。Liu等對中國蘭新高鐵復雜地形的強風工況下車體側滾角、橫向位移等橫向振動特性進行了測試，其測試結果也表明，強風工況對車體橫向振動影響顯著。

貨運動車組由于其裝載貨物的特性，其振動的穩定與否直接影響運輸的效率，有鑒于此，為探究橫風對貨運動車組振動的影響，本文分析了貨運動車組在橫風作用下車體及其裝載的集裝器的加速度及其振動特性關系，以便找到橫風載荷作用下貨運動車組的振動規律。

1 風載荷模型

1.1 風速模型

橫風穩定性近些年來成為國際鐵路行業的研究熱點。在風致安全性與穩定性的研究中，通常會采用三種風譜模型，分別為定常穩態風譜模型、中國帽風載模型和非穩態風載模型。定常穩態風載模型基于均勻風假設，氣動載荷設置為恒定力。然而，環境中的自然風并不是定常穩態風，而是一種在空間上和時間上平穩的隨機過程，具有一定的物理隨機特征。自然風可看成由速度不變的穩態風和速度瞬變的脈動風組成。中國帽風載模型考慮風的瞬態效應，在平均風速下加入瞬時增加呈指數分布的瞬時風速，如圖1所示，該模型可用來評估列車運行的瞬時安全性。定常穩態風載模型和中國帽風載模型均不可用來評估風致載荷對列車振動及二者相互作用所產生的影響。第三種模型——非穩態風載模型可解決這一問題。非穩態風載模型可模擬風速的脈動效應，考慮了風載的振動頻率，采用統計方法還原大氣邊界層的空間一時間分布規律。其脈動風速的大小受風速功率譜密度、風載頻率等因素的影響。常用的非穩態風載風譜密度函數主要有Davenport風譜，由Kaimal譜演化的Simiu譜，以及Cooper風譜。Davenport風譜和Simiu風譜多用于評價與分析橋梁及建筑結構的風致安全性，其中Simiu譜還是中國《公路橋梁抗風設計規范》中建議采用的風譜，兩種風譜均在車輛動力學仿真中有所應用。例如，Simiu和Scanlan提出了車輛氣動導納函數的概念，并將這一概念運用在列車多體動力學仿真中。夏禾等基于Davenport風速功率譜，分析了風和車輛荷載同時作用下車橋系統的動力可靠性。本文將采用2008年了SI標準和2010年的ENl4067-6標準中給出的評定列車動態響應的非穩態風譜——Cooper風譜，該風譜是基于vonKarman譜提出的基于列車周圍湍流風的隨機過程模型，其公式表征如下

文獻基于Cooper理論對列車周圍的氣動導納函數和氣動權重函數進行了一系列研究與驗證。基于該風譜，很多學者對列車在風致載荷下的可靠性和載荷譜進行了一系列研究，Yu等采用諧波疊加后的Cooper風譜，基于模糊隨機可靠性的方法對高速列車的橫風穩定性進行了研究。繆炳榮等采用線性濾波后的Cooper風譜作用于高速列車，評估其列車運行安全性，并提取車體結構載荷時間歷程，編制出了典型的車體結構風致載荷譜。

結構的風振效應分析應以風速時程模擬為基礎，在風速時程的各種模擬方法中，基于蒙特卡洛思想的諧波疊加法和線性濾波法應用最多。這兩種方法適用于任意指定譜特征的平穩高斯過程。下式為諧波疊加法得到的離散頻率n_j的脈動風速

圖3和4分別給出了無量綱頻譜圖和仿真風譜密度圖，圖中風譜的頻率特性和與Coopcr理論仿真風譜的擬合情況均與文獻中相似，說明該風譜的擬合性較好，可用于進一步分析。

1.2 高速列車氣動力計算

當列車運動時，側偏角是始終隨時間變化的。

由于風場中的列車位置時刻變化，其側偏角也一直變化。

文獻中采用將脈動氣動載荷和平均氣動載荷分開計算的方法，總的氣動載荷為脈動氣動載荷和平均氣動載荷之和，即：

考慮到作用在列車上的氣動載荷與列車周圍的湍流風速存在一定的時滯效應，文獻中引入氣動權重函數h_F（τ）可以反映出這種時間延遲效應。式中 τ為無量綱延遲時間。

文獻指出，采用權函數法計算的瞬態風載荷作用下，列車受到的力與準靜態計算結果相比存在0.05s的滯后時間，而模擬的風載荷結果與準靜態計算結果基本相等，因此可直接采用準靜態的計算結果來代替瞬態的計算結果。

由以上氣動載荷公式可看出，列車確定后，影響氣動載荷的主要是氣動系數。氣動系數可根據CFD數值仿真或風洞試驗獲得。由于截至目前，貨運動車組車型設計方案還未出臺，因此，本文借助高速客運動車組的氣動力系數，其公式如下：

文獻指出側滾力矩系數和側力系數對高速列車在橫向非穩態風載下的運用安全性影響最大，考慮到橫向側風載荷與側滾力矩的存在均嚴重影響高速列車的振動特性，為深入探究貨運動車組橫向振動特性與非穩態橫風載荷的關系，并考慮到車輛橫向運動與垂向運動的弱耦合性，對車體施加與橫向運動相關的側向風力載荷和側滾力矩載荷，如圖6所示。

實際情況下，無論是風速公式還是側偏角公式，均為時變歷程，每一時刻點均有與之對應的該點的瞬時合成風速和瞬時側偏角，因此，時變的氣動載荷可按如下氣動公式進行計算，即：

兩種方法計算得到的每3.4m²面積上的氣動載荷時域和頻域對比如圖7和8所示，由圖中可見，兩種方法計算得到的氣動載荷在時域和頻域上相似性較好，振動幅值與頻率差別不大，當必須考慮脈動風載荷的時滯效應時，可用文獻中的方法進行代替。

由圖8可見，側風載荷的主要頻率峰值區段集中在2Hz以內。由于軌道車輛的一階固有頻率一般在0.5-1Hz，自然風的非靜態分量必然會引起車體或其內部承載物的動態響應。

本文采用公式（17），（18）直接計算氣動載荷。

2 貨運動車組動力學建模

考慮風載和軌道激勵的車體動力學公式如下式所示

式中 y（t）為車體位移，M，C，K分別為車體的質量矩陣、阻尼矩陣和剛度矩陣，f_w（t）為作用于車體的風載荷，f_t（t）為軌道激擾所產生的輪軌作用力。

圖9給出了貨運動車組集裝器布置的一種方案，按照該方案，本文以某型車動車組中間車動力學參數為基礎，建立了貨運動車組的車體-集裝器系統動力學模型。模型分別考慮了輪對、構架、車體和各集裝器縱、橫、垂、側滾、點頭、搖頭等6個自由度。貨運動車組內集裝器由設置在地板上沿車體縱向布置的4個橫向止檔器和4個雙固定爪禁錮裝置進行限位，雙固定爪用于集裝器的縱向和垂向限位，橫向止檔器用于集裝器橫向限位，端部止檔器用于端部集裝器的縱向限位。在此，將上述連接方式簡化為集裝器四角處于車體間的縱、橫、垂三向力元連接，其連接剛度均取為10MN/m。基于這種車體-集裝器的耦合特性，文獻給出了與車體耦合的集裝器的運動方程，在此不再贅述。本文模型中車輪和鋼軌的類型選擇LMa/CHN60匹配。

一般情況下，風載荷在車輛動力學模型中采用力的平移和等效原則，將作用于車體表面上的分布壓力向車體某一點簡化，得到作用于車體某一點的集中力和力矩，通過簡化可獲得風載作用于車體上的氣動力。然而，考慮到貨運動車組承載貨物的特殊性，將氣動載荷向車體某一點集中極有可能出現力傳遞到車輛承載的集裝器后不均勻的現象，為解決此問題，本文采用多點離散加載風載荷的方法進行處理，即將風載在車體上每3.4m²集中加載，車體總側面積取為75m²。風載荷加載示意圖如圖11所示。這樣既滿足列車中集裝器受力的需要，也可較好地仿真風載荷實際作用于車體上的特性。由于貨運動車組擬運行線路為高速鐵路，因此選取中國實測高速軌道譜——武廣軌道激擾譜作為整車的軌道激勵輸入，車輛運行速度選取為250km/h。

3 非穩態橫風載荷激勵對車體和集裝器的橫向振動影響

非穩態橫風載荷激勵作為車輛系統的外部激勵源，與軌道不平順激勵一樣，均會造成車輛系統振動特性在時域和頻域的改變。

3.1 風速對車體與集裝器橫向振動影響

由文獻可知，風速對車輛的橫向振動有不可忽視的影響。考慮到同一車廂內裝載集裝器的裝載位置、大小和載重不同，為較全面探究橫風風速對貨運動車組車體和其裝載集裝器橫向振動的影響，選取圖9中的1號、5號、11號和17號集裝器，以反映同一車廂內相同型號集裝器裝載位置不同對橫向振動規律的影響。

依據前述不同風速的橫風載荷的獲取方法及施載方式，得到平均風速5-20m/s的車體和集裝器在風載激勵下及風載和武廣軌道不平順激擾耦合作用下的橫向加速度的均方根值，如圖12和13所示。由圖12和13可見，當平均橫風風速由5m/s增大到20m/s時，車體和集裝器的橫向加速度RMS值均隨之增大，車體與集裝器的橫向振動在每個風速作用下的規律幾乎一致。主要表現為，當僅有風載激勵作用時，車體內部集裝器橫向加速度RMS值均大于車體，不同擺放位置的集裝器的橫向加速度RMS值差異不大，當風速由5m/s增大至20m/s時，車體和各集裝器橫向加速度RMS值均增大了約4.5-5倍左右;當車輛在風載和軌道激擾耦合作用下，1號集裝器在各風速作用下，其橫向振動均小于車體，11號和17號集裝器均大于車體，5號集裝器除在平均風速10m/s的其他各風速作用下，其橫向加速度RMS值均小于車體，隨著車速的增加，車體和各集裝器橫向加速度RMS值分別增大了82.0%，103.2%，61.6%，39.9%和28.3%。圖12和13的差異性由軌道激擾引起，當車輛僅有軌道激擾作用時，車體及上述各集裝器的橫向加速度RMS值分別為0.70，0.35，0.52，0.58，0.80m/s²，由此可見，軌道激擾對車體和17號集裝器的橫向振動的影響處于平均風速10和15m/s的影響之間，而對1，5，11號集裝器的影響處在平均風速5和10m/s之間。當橫風載荷與軌道激擾耦合作用時，受到軌道橫向激擾方向瞬變的特點影響，二者振動疊加后便產生了如圖13所示的橫向加速度變化規律，由于軌道激擾對各集裝器振動能量的不同，當其疊加了相似的風載振動能量，導致了耦合激勵下各集裝器橫向振動加速度的增大幅值的差異。

3.2 車體及集裝器橫向振動頻域分析

由圖12和13可見，非穩態橫風載荷對貨運動車組車體一集裝器系統的橫向振動加速度影響比較突出，這種影響不僅表現為時域特征上，還表現在頻域特征上。為深入研究頻域特征的差異性，選取車輛系統在僅有武廣軌道激擾、僅有橫風載荷作用的工況，以及武廣軌道激擾和橫風載荷耦合作用的工況，將其橫向加速度時間歷程圖進行傅里葉變換，得到其頻域特征。基于3.1節分析可知，不同風速下車體及其集裝器橫向振動規律相似，因此，選取了橫向振動能量較大的平均橫風速度20m/s的工況進行了以下分析。

圖14-16分別給出了貨運動車組車體和不同位置集裝器在上述三種外部激勵作用下的橫向振動功率譜。在外部激勵作用下，車體與集裝器的振動能量多集中在15Hz以內。軌道不平順激勵作用下的車體與集裝器橫向振動能量較之平均風速20m/s的風載工況和耦合激勵工況低了約一個數量級。僅在不平順激勵工況下，車體橫向振動在2.46-4.80Hz內存在一個能量最高的頻段，橫向振動能量峰值在4.10Hz處，在1.50Hz左右存在能量次高頻段;集裝器除在10Hz以內存在與車體較為一致能量峰值頻段外，在23.97Hz處也存在一能量振動峰值，該頻率與車輛車輪的轉頻一致。集裝器10Hz以內的1.50-3.03Hz的振動能量按集裝器擺放位置由中心向兩端振動能量逐漸增加，尤其在1.50和2.03Hz左右的能量增加更為突出，其橫向振動能量已遠大于車體，也即該段能量在經過車體傳遞到集裝器后出現了振動能量放大效應。23.8Hz處的集裝器橫向振動能量按集裝器擺放位置由中心向端部呈逐漸減小的趨勢，但變化幅值不大。

由圖15可見，由于作為低頻激擾的橫風載荷直接作用于車體，該載荷傳至集裝器僅經過連接件的一級傳遞，使得非穩態橫風載荷對車體-集裝器耦合系統的橫向振動頻域影響較大。非穩態橫風載荷作用下，車體和集裝器的振動能量主要集中在10Hz以內，其中車體的橫向振動能量主要集中在1.17-3.57Hz，尤以1.90Hz處的能量最高。集裝器在此頻段內能量也較高，且其大小隨集裝器擺放位置由中心向端部略減小。此外，集裝器除在上述頻段內存在較大能量外，在0.3-1.17Hz內，其橫向振動能量更高，該頻段內的橫向振動能量隨集裝器擺放位置由中間向端部呈逐漸增加的趨勢，其能量最大峰值在0.53Hz處，并在0.77和0.37Hz頻率處存在橫向振動能量次高峰值。考慮到風載荷能量區間在2Hz以內，并在上述頻段處同樣存在能量峰值點，可以確定該能量峰值由風載引起。

圖16為非穩態橫風載荷和軌道不平順耦合激擾下車體與不同位置集裝器的橫向振動功率譜。由該圖可見，均速20m/s的橫風載荷相較于軌道不平順激擾對車-貨耦合系統的影響更大，在圖14和15中主要表現在頻域上的相似性。耦合激勵和僅非穩態風載作用下，車體的橫向振動能量均集中在10Hz以內，且車體的振動能量在1.9Hz處存在橫向振動峰值，集裝器均在0.37，0.53和0.77Hz左右處存在橫向振動峰值，與僅非穩態風載作用的結果不同的是，系統在耦合激勵作用下，車體在1.90Hz處的橫向振動能量得到了一定的衰減。對于集裝器，耦合激勵作用下，其橫向振動能量隨其擺放位置由中部向端部呈增加趨勢，相較于僅風載作用工況，集裝器在1.50和1.90Hz處的振動能量有所增加，且隨集裝器擺放位置由中部向端部增加幅度逐漸增大，這兩處的振動峰值可能為耦合激勵與集裝器固有振動頻率發生耦合作用引起。

為確定圖16中車體與集裝器在1.50與1.90Hz處的橫向振動峰值由風載和軌道激擾與集裝器振動耦合作用引起，計算了平均風速5m/s作用下非穩態風載和軌道不平順耦合激擾下車體和集裝器橫向振動功率譜，如圖17所示，5號集裝器、11號集裝器和17號集裝器的橫向振動均在1.50，1.90Hz存在能量振動峰值，且該振動能量隨著集裝器擺放位置由中部向端部移動而逐漸增大，此規律與平均風速20m/s時的耦合激勵作用工況的結果一致。由于兩種風速風譜頻率一致，二者區別僅限于風譜能量不同，表現在圖16和17中為0.37-0.77Hz的橫向振動能量的差異性。

3.3 車體至集裝器橫向振動傳遞特性研究

由以上分析可知，不同擺放位置處的集裝器橫向振動特性出現了較大的差異性，由于集裝器與車體經過相同的力學元件連接，集裝器的橫向振動與車體的橫向振動息息相關，為了深入了解集裝器擺放位置對各種激擾下橫向振動傳遞率的影響，分析了平均橫風風速20m/s下，車體至工號、5號、11號、17號集裝器的橫向振動幅頻傳遞函數如圖18所示。

由圖18（a）可見，車輛系統僅有風載作用時，頻率在1.47Hz以內時，車體到集裝器的橫向振動傳遞函數均在1以上，其中在0.77Hz左右為橫向振動傳遞峰值。當風載激勵與軌道不平順激勵耦合作用時（圖18（b）），1.47Hz以內的橫向振動傳遞函數與圖18（a）類似，也均大于工，但與其不同的是，在0.77Hz處的振動傳遞函數值有所降低，在1.0和1.29Hz左右多出了傳函峰值，圖18（a）處的1.47-3.13Hz低于1的傳函峰值在圖18（b）中也有所增加，此處的橫向振動傳遞函數在1上下波動，造成此處現象的原因為軌道激擾造成橫向振動幅頻傳遞函數的疊加作用。由圖18（c）可見，當軌道不平順激勵作用于車輛系統時，在圖14中集裝器橫向振動能量較高的1.5-3.03Hz左右，5號、11號、17號集裝器的橫向振動傳函均大于1，各集裝器的橫向振動傳遞函數大于1的頻率范圍也隨其擺放位置由中部到兩側而逐漸加寬，這也解釋了圖14中集裝器在1-1.23Hz左右的振動能量逐漸突出的原因。

綜上所述，橫風載荷對貨運動車組內的集裝器的橫向振動在低頻處的影響不容忽視。

4 結論

本文基于C00pcr理論構建均速20m/s的非穩態橫風風譜，獲得該風譜相應的隨機側風載荷和側滾力矩載荷，將其施加到貨運動車組動力學模型中，計算分析了勻質集裝器重心高度為其幾何中心處時，貨運動車組車體-集裝器系統在風載激勵和風載與軌道不平順耦合激勵作用工況下不同風速的橫向加速度RMS值的變化規律以及該系統在風載激勵、武廣軌道不平順激勵和兩種激勵耦合作用工況下的車體、不同部位集裝器橫向振動的頻域特性。通過以上分析，得到以下結論：

（1）非穩態橫風載荷工況和橫風載荷與軌道不平順激擾耦合作用工況下，車體與集裝器的橫向加速度RMS值均隨橫風平均風速的增加而增加。非穩態橫風載荷工況下，車內擺放于不同位置的集裝器的橫向加速度RMS值均大于車體的橫向加速度RMS值;兩種激擾耦合工況下，處于車體較中部的集裝器的橫向加速度RMS值小于車體，而處于較邊側位置的集裝器則大于車體。

（2）平均風速20m/s非穩態橫風載荷與軌道不平順激勵耦合作用工況下，非穩態橫風載荷在兩種激勵造成的車體與集裝器的橫向振動的比重遠大于軌道不平順激勵所占的比重，其橫向振動能量也比軌道不平順激勵造成的車體與集裝器的橫向振動能量高出一個數量級。

（3）非穩態橫風激勵和軌道不平順激勵耦合作用工況下，車體橫向振動能量集中在1-5Hz，其橫向振動峰值在1.90和1.63Hz;集裝器橫向振動能量集中在0.3-5Hz，尤以工Hz以內的橫向振動能量更高，并存在0.53，0.77Hz等多個振動峰值。軌道不平順激勵工況下，車體橫向振動能量集中在1-9Hz以內，峰值為4.10Hz左右，集裝器的橫向振動除在上述頻段內的能量集中外，在23.8Hz即車輪轉頻處存在一定的振動響應。總體來看，受集裝器在車廂內擺放位置的影響，使各集裝器橫向振動能量隨其在車廂內由中心向兩端移動逐漸增大。表現在軌道不平順工況中邊側集裝器逐漸激起了1.50和1.90Hz的能量峰值，表現在另外兩種工況中為集裝器峰值能量的增大。

（4）受橫風和軌道不平順激勵耦合作用下車體至集裝器橫向振動幅頻傳遞函數疊加的影響，與僅風載激勵工況和僅軌道不平順激勵工況相比，耦合激勵工況下橫向振動能量較高的低頻范圍內（10Hz）的橫向振動幅頻傳遞函數在工或遠大于工，這表明，更接近實際工況的耦合激勵工況對貨運動車組車體-集裝器系統的橫向振動的影響不容忽視。

該研究結果對常經過大風線路的貨運動車組的裝載方案具有一定的指導意義。