基于Polar插值改進的結構振動信號壓縮采樣正交匹配追蹤恢復算法

康杰 段忠東

摘要：壓縮感知是近年來出現的采樣和信號處理方法，它利用了信號中普遍存在的稀疏特性，從而可以以遠低于奈奎斯特頻率的采樣速率采集壓縮樣本，并依概率恢復得到真實信號。結構振動信號具有一定的稀疏性。對其進行壓縮采樣并進行信號重構，離散傅里葉原子的頻率往往與信號實際頻率不匹配，造成頻率泄漏，降低信號重構精度。針對離散原子庫存在的缺陷，采用Polar插值對正交匹配追蹤（Orthogonal Matching Pursuit，OMP）算法進行了改進。以OMP算法選擇的最優原子為基礎，利用Polar插值在最優原子臨近構建頻域連續原子庫，構建了信號重構的優化模型，通過凸優化算法獲得實際頻率的最優估計。改進算法以較小的計算量實現對OMP算法得到的離散原子頻率的修正。通過對結構振動的數值模擬和對模型試驗壓縮信號的重構，結果表明，與常規算法相比，改進算法可有效提高信號重構精度，特別是在壓縮觀測值數量較少的情況下，精度提升效果更加明顯。

關鍵詞：結構振動;壓縮感知;OMP算法;Polar插值;連續原子庫

中圖分類號：O327;TN911.7文獻標志碼：A 文章編號：1004-4523（2020）03-0450-09

DOI：10.16385/j.cnki.issn.1004-4523.2020.03.002

引言

壓縮感知（Compressed Sensing，CS）是近年來出現的一種新的信號采集和處理理論。CS理論指出，對于在信號本身或者在某種變換下具有稀疏性的信號，僅需采集少量壓縮觀測值（相比奈奎斯特采樣樣本）即可高精度地重構出原始信號。與奈奎斯特采樣定理相比，CS理論充分利用了信號稀疏性，能夠極大地減少信號的采集與傳輸。此外壓縮觀測值具有均等性，在數據傳輸過程中，丟失部分觀測值對信號重構幾乎沒有影響。基于以上優勢，國內外針對CS理論開展了大量研究工作，其應用領域涉及單像素相機成像，醫學核磁共振成像，雷達成像，數據通信，無線傳感網絡，結構健康監測等。

信號稀疏性是壓縮感知理論應用的重要前提。對于頻域稀疏信號，一般通過離散傅里葉原子庫對其分解來獲取稀疏性。然而離散傅里葉原子庫包含的頻率信息十分有限，僅對應頻域范圍內一組離散點，無法與信號中任意分布的頻率成分精確匹配，這在一定程度上損害了信號的稀疏性。增加原子數量可使原子庫包含更多頻率信息，能夠有效提高信號稀疏分解質量，但原子之間的強相關性對CS重構算法挑選原子產生負面影響。一些改進方法隨之產生，Dai等在原子選擇過程中通過回溯思想來優化原子挑選質量;Duarte等提出采用受限聯合子空間信號模型來提高選擇原子準確性。雖然這些方法恢復信號精度有所增加，但依然受到離散原子庫頻率信息不足的影響。

一些研究人員開始探討在頻域連續區間上尋找原子進行壓縮感知信號重構。Ekanadham等通過Polar插值圓弧近似構建頻域連續原子庫，并在此基礎上與BP算法結合提出了CBP算法。Polar插值連續原子庫可以有效覆蓋信號包含的頻率成分，因此CBP算法重構信號精度較高。Tang等基于原子范數概念提出了SDP算法，將稀疏信號重構問題轉化為求解半正定方程，徹底擺脫了離散原子庫的束縛，從而獲取了較高的信號恢復精度。值得注意的是，無論CBP算法還是SDP算法，在信號重構過程中都會產生巨大計算量，在處理大規模信號重構問題時存在較大困難。

本文出發點在于探討如何以較小的計算量獲取高質量的重構信號。OMP算法在重構信號過程中具有復雜度低、效率高等特點，但算法精度受到離散原子庫的限制。而Polar插值能夠在頻率參數點附近構建連續原子庫，具有較好的靈活性與可操作性。因此采用Polar插值對OMP算法進行改進，增加較小的計算量來提高信號重構精度。在基于離散原子庫重構信號過程中，OMP算法所挑選出的原子頻率參數與信號頻率成分存在一定誤差，采用Polar插值在已挑選原子頻率參數附近構建連續原子庫，通過凸優化算法對挑選的原子頻率參數進行校正，提高信號重構精度。本文利用結構振動信號的頻域稀疏性，通過數值模擬和模型試驗獲得壓縮觀測值，采用本文提出的改進算法進行信號重構，結果表明，對于理想頻域稀疏信號，改進算法可有效提高信號重構精度，特別是在壓縮觀測值數量較少的情況下，精度提升效果更加明顯。而對于近似稀疏信號，改進算法也能在一定程度上提升信號重構精度。

1 基于Polar插值改進的OMP算法

壓縮感知理論中，壓縮矩陣φ為扁平矩陣，即其行數遠小于列數。按式（2）得到的壓縮信號y的觀測值數要遠小于信號x的維數，即對信號x進行了壓縮。這個壓縮過程在物理實現上一般是在模擬信號階段實現的。在對x進行壓縮采樣后，目標就是如何通過壓縮觀測值y重構原信號x。下面通過構建基于Polar插值的連續字典庫，結合OMP算法來提高信號重構的精度。

式（1）中信號模型易采用函數sin（2πf_dt）與COS（27πf_dt）生成加密原子庫D_s與D_c：

2 數值實驗

下面通過數值實驗對采用Polar改進的OMP算法（這里稱之為IOMP算法）進行測試。一個3自由度阻尼系統用于生成結構振動信號，如圖2所示。

系統質量塊之間以及質量塊與邊界之間采用彈簧阻尼單元連接。系統的質量矩陣，剛度矩陣和阻尼矩陣如下所示：

激勵荷載由6條正弦信號疊加而成，其頻率分別為f₁=0.1699Hz，f₂=0.7144Hz，fa=1.0498Hz，f₄=0.73Hz，f₅=2.6579Hz與f₆=2.7199Hz。其中f₁，f₂和f₃對應于體系的前3階自然頻率。激勵荷載施加于m₁，從m₂采集振動信號。采樣頻率設置為10Hz，采樣點數為1000.

2.1 原子數量及噪聲水平對IOMP算法重構信號精度的影響

表1對比了不同原子數量與噪聲水平下IOMP算法重構信號精度，各工況觀測矩陣φ均采用隨機伯努利矩陣，即該矩陣的元素隨機取1或者-1，信號混入的噪聲為高斯白噪聲，Polar插值連續區間參數△選為0.1Hz。本文采用相對誤差ξ來衡量重構信號精度。相對誤差是對重構信號質量進行整體描述，相對誤差越小，則重構信號精度越高。相對誤差計算公式如下

由表1可知，原子數量和噪聲水平對IOMP算法重構信號的精度有重要影響。當噪聲水平較高或原子數量較少時，IOMP算法重構信號誤差較大。這是由于OMP算法初選原子的頻率參數精度過低，致使Polar插值連續原子庫無法覆蓋到信號的真實頻率。增加觀測值和原子數量可以提高信號恢復的精度，如噪聲水平為20%，IOMP算法在原子數量為5000，壓縮值數量為10%條件下重構信號精度要明顯高于原子數量1000，壓縮觀測值5%條件下重構信號精度。

2.2 Polar插值連續△對IOMP算法重構信號精度的影響

圖3對比了△不同取值下IOMP算法重構信號的精度，信號噪聲水平為10%，壓縮矩陣φ采用隨機伯努利矩陣，觀測信號壓縮比為5%。圖4對比了原始信號和重構信號的時程。

圖3（a）顯示當原子數量為1000，IOMP算法重構信號誤差在△=0.4Hz時最小。這是由于原子數量過少導致OMP算法初選原子頻率參數存在較大誤差，需要Polar插值連續原子庫在大范圍內對原子頻率參數進行調整，因此當厶增加至0.4Hz時IOMP算法重構信號誤差最小。當原子數量為2000-4000，OMP算法初選原子頻率參數精度較高，只需Polar插值連續原子庫在較小的范圍內對頻率參數進行調整即可，此時IOMP算法在△=0.1Hz時達到了較高的重構精度。此外，當△=0.7Hz時IOMP算法重構誤差均較大。這是由于原子d_e（f）=e_i2πft頻率參數f在△上變化時，其運動軌跡為多維球面上一段曲線，厶越大則曲線段越長，此時以Po-lar插值圓弧近似相應曲線段存在較大誤差，從而降低了算法重構信號精度。基于以上分析，IOMP算法重構信號需要合理選取原子數量與參數△值，一般情況下原子數量不少于4倍信號長度，△值不易大于10倍采樣頻率與采樣點數的比值。圖4中信號時程顯示，恢復的信號與原信號吻合很好。

3 模型試驗

此節采用模型試驗數據對IOMP算法進行測試。如圖5所示，模型層高為0.48m，總高度為1.56m，每層板重量為20.272kg，模型總重量為67.44kg，模型底部與臺面固接。在模型第3層沿x軸向施加錘擊荷載，加速度傳感器在模型第2層板采集x軸向結構振動信號。圖5中，①為荷載施加位置，②為傳感器位置。振動信號時程共采集1000個加速度樣點，采樣頻率設置為50Hz。

3.1IOMP算法與其他主要壓縮感知算法重構信號精度比較

目前壓縮感知理論已發展了大量壓縮信號重構算法，然而在重構頻域稀疏信號時，多數重構算法易受離散傅里葉原子影響產生重構誤差。表2對比了IOMP算法與其他主要壓縮感知算法重構信號精度，表中計各工況壓縮矩陣φ同樣為隨機伯努利矩

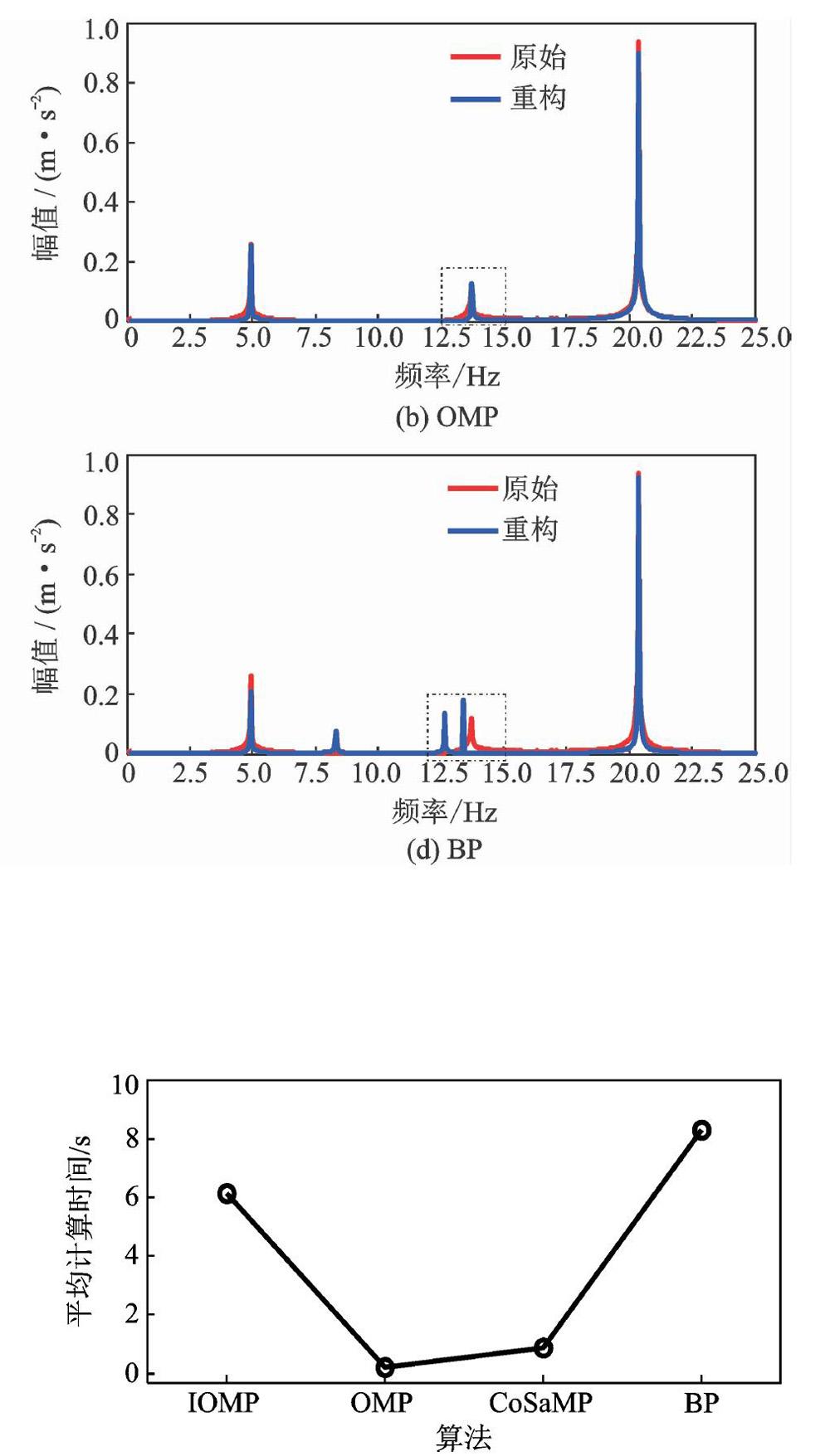
貪婪迭代算法與凸優化算法是兩大類壓縮感知重構算法。貪婪算法復雜度低、計算效率高，而凸優化算法需要求解優化方程，因此算法復雜度、高計算效率低。圖8對比了各算法計算平均時間，OMP算法與CoSaMP算法屬于貪婪算法，計算耗時較少。BP算法屬于凸優化算法，計算耗時較多。IOMP算法在OMP算法基礎上需要求解一個規模較小的凸優化方程，因此計算時間介于CoSaMP算法與BP算法之間。

陣，Polar插值參數△取值為0.2Hz。

對于圖6中的頻域稀疏信號，IOMP算法重構信號精度優于其他主要壓縮感知重構算法。當原子數量為5000，IOMP算法重構信號誤差為0.1718，OMP算法與BP算法重構信號誤差均較大，分別為0.2916與0.2868.而基于OMP算法改進的Co-SaMP算法重構信號精度與IOMP算法接近，其為0.2019.

信號重構誤差大小影響其傅里葉譜的精度，原始信號和恢復信號的傅里葉譜如圖7所示。IOMP算法與CoSaMP算法重構信號頻譜較為光滑且與原始信號譜吻合較好，頻譜出現的3個峰值與原始信號譜準確對應。相比之下，OMP算法與BP算法重構信號頻譜在原始信號第二個峰值處出現較大偏差，此外BP算法重構信號頻譜還存在較多毛刺。

3.2 基于重構信號進行模態參數識別

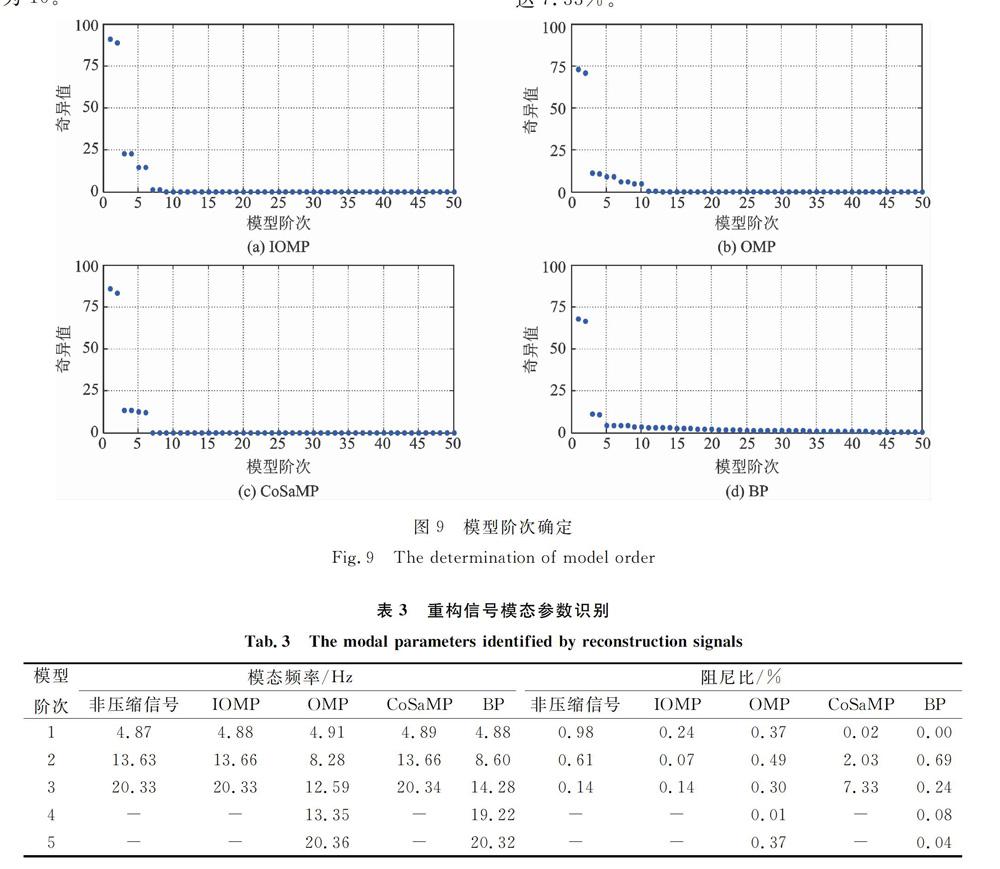
以圖7中的重構信號作為輸入，采用EAR（Eigensystem Realization Algrithm）算法來識別模態參數。模型階次確定如圖9所示，IOMP算法與CoSaMP算法重構信號隨著模型階次增加奇異值出現明顯跳躍，因此模型階次確定為7.而OMP算法與BP算法重構信號此現象并不明顯，模型階次選為10.

采用重構后的信號對結構模態參數進行識別，結果如表3所示。IOMP算法與CoSaMP重構信號誤差較小，ERA提取的模態頻率精度較高;OMP算法與BP算法信號重構誤差較大，導致EAR提取模態參數不僅精度低且存在虛假模態。然而，阻尼參數對恢復信號的誤差更敏感。如表3所示，用恢復后的信號對阻尼比識別結果不理想，特別是基于CoSaMP算法重構信號獲取的第3階模態阻尼比高達7.33%。

4 結論

本文采用Polar插值連續原子庫對OMP算法進行改進，達到了以增加適當計算量較大程度地提高重構信號精度的效果。本文針對振動壓縮采樣信號，建立了基于Polar插值的OMP信號重構的凸優化模型，并采用凸優化算法進行求解。通過數值模擬和模型試驗對該算法進行了驗證。結果表明，相比常規壓縮感知算法，IOMP算法能夠以較少的觀測值高精度地重構頻域稀疏信號;利用重構信號進行模態參數識別，避免了虛假模態的出現，提高了模態參數識別結果的精度。